基于贝叶斯推断的脉冲星偏振位置角拟合算法

陈威威, 王洪光, 张颜荣



基于贝叶斯推断的脉冲星偏振位置角拟合算法

陈威威, 王洪光, 张颜荣

(广州大学物理与电子工程学院, 广东广州, 510006)

脉冲星辐射束的偏振位置角与相位的关系可用旋转矢量模型(RVM)描述, 现有的Levenberg-Marquardt非线性拟合和格点搜寻算法对RVM的拟合存在效率低、易过拟合等问题。本文发展了一套基于贝叶斯推断的马尔可夫链蒙特卡洛算法(MCMC), 并用该方法对已有文献中的10颗脉冲星偏振位置角进行了拟合。结果表明, MCMC算法不仅能得到与已有文献一致的结果, 而且该算法具有高效、不易过拟合、能更好地估计参数的可信度区间等优点。

脉冲星; 辐射束; 偏振位置角; 旋转矢量模型

脉冲星是一种快速自转的致密天体, 具有超强的磁场, 整体上是一个偶极磁场。在星体表面附近可能存在多级场, 通常认为其射电辐射来源于磁层中偶极场占主导的区域, 其旋转矢量模型如图1所示。偶极场磁轴与自转轴之间的夹角称为磁倾角(), 观测者视线与自转轴之间的夹角称为视线角(), 而视线与磁轴之间的最小夹角通常被称为撞击角(), 这3个角度只有2个角独立, 且满足方程=+。脉冲星的辐射来源于其磁层, 在上述与辐射几何相关的3个角度不同的情况下, 观测者看到的现象会有差异, 磁层中的动力学过程也与磁倾角密切相关, 因此, 如何从观测中确定磁倾角和撞击角(或视线角)是脉冲星研究中的重要课题之一。1969年Radhakrishnan和Cooke[1]提出了旋转矢量模型(Rotation Vector Model, RVM), 给出了磁倾角、撞击角和线偏振位置角的几何关系:

其中0和0为磁轴与自转轴所在磁力线平面对应的相位和线偏振位置角。线偏振位置角可以从偏振观测数据中的Stokes参量计算出来, 因此通过使用RVM, 可以拟合出、、0以及0。相比其他确定和的方法, RVM拟合被认为是最简洁可靠的方法。目前用这类方法限定了和的脉冲星不到90颗, 较为系统性的有Everett等[2]、Keith等[3]、Rookyard等[4]的工作。目前主要使用2种方法来拟合和, 一种是格点计算, 将定义域划分为一定数量的格点, 通过计算各格点参数值下的2来寻找最优参数值; 另一种是介于高斯—牛顿法与梯度算法之间的Levenberg-Marquardt(简称LM)[5]非线性拟合方法, 该方法借助模型对函数进行求导, 寻找2的极小值点。

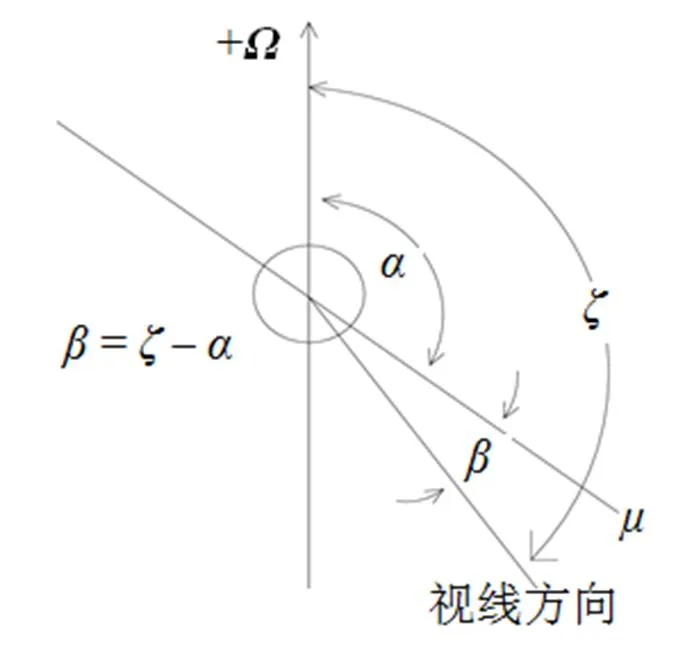
图1 磁倾角α与撞击角β

Rookyard等人[4]使用格点搜索的办法拟合RVM, 得到了26颗脉冲星的和限定结果。这种方法面临的问题有: (1) 在多维情况下计算量巨大, 耗时长; (2) 由于没有明显的优化路径, 极大地消耗计算资源; (3) 精度受限制。

在Everett等[2]和Keith等[3]的工作中, 他们使用LM算法对磁倾角与撞击角进行拟合, 分别给出10颗和5颗脉冲星的磁倾角和撞击角的最优拟合值。在其他文献中有不少也沿用这种方法[6]。LM以及其他类似算法的特点是优化路径朝着极值点推进, 沿着2减少的方向取参数值, 直至找到局部极值点。在RVM的拟合中, 使用此方法将会面临几个问题: (1) 优化路径的选择过度依赖2的大小, 容易导致过拟合; (2) 优化路径以及最后的极值点容易受初始值的影响, 最终停在局域极值点; (3) 这种优化方式更关注极值点, 对置信区间的分析能力较弱; (4) 在每换一套参数值后, 都要重新对似然函数进行求导, 当参数维度较高时, 计算量将急剧增大, 耗时长。Everett等[2]指出, 使用LM算法的主要困难在于和存在强相关, 在偏振位置角曲线相位较窄或数据对RVM有一定程度偏离的情况下, 拟合程序有时会给出趋向于180°或者0°及趋向于0°的结果, 这就是所谓的过拟合现象(尽管这仍符合RVM的数学关系)。发生这种情况的时候,2在(,)趋向于(180°, 0°)或(0°, 0°)的角落缓慢地减少。这种现象在0与0作为自由参量的情况下尤为严重, 拟合程序有时锁定在一组(0,0), 使得无法在降低χ2值的同时避免出现过拟合。为了减轻该问题的影响, Everett等[2]加入了Powell[7]拟合算法, 先改进初始值的选择, 再把改进了的初始值输送到LM算法中进行拟合。他们首先使用其他研究者给出的结果作为初始值, 再手动微调0与0来拟合数据, 最后使用拟合程序对、、0和0一起拟合。过拟合问题的存在不仅增加了拟合的繁琐程度, 不利于大样本的自动化拟合, 而且也限制了此方法所能处理的脉冲星样本。

鉴于以上2种方法存在的问题与不足, 有必要发展新的拟合和参数的方法。马尔科夫链蒙特卡洛(MCMC)方法是一种基于贝叶斯推断, 能适用于多参数拟合的有效方法, 在宇宙学等许多天文领域都有应用, 但在限定脉冲星辐射几何的研究中还未见应用。本文将使用该方法对参数和进行拟合, 并与已有文献结果进行对比分析。

1 基于贝叶斯推断的MCMC拟合方法

MCMC是一类基于贝叶斯推断的、通过建立以目标后验分布为平稳分布的马尔科夫链并对其进行采样的算法。有了后验分布, 模型参数的最可能值及其可靠取值范围即可从中获得。这类算法的思路是: 为了得到未知的模型参数在其取值空间中的概率分布(后验分布), 可以先猜测一个初始的分布(先验分布), 通过和观测数据的比对来修正猜测, 其用到了贝叶斯推断的原理。修正的过程是不断地从已知的分布(最初猜测的和后来调整的)中采样得到当前参数值, 再按照马尔科夫链平稳分布的要求产生新参数值的过程。理论上, 被更新的参数值的分布应当不断逼近目标后验分布, 当马尔可夫链收敛时, 大量的参数值达到稳定的统计分布, 便近似得到后验分布, 拟合过程结束。MCMC有多种对参数值进行采样和更新的策略, 本文采用了Metropolis-Hasting算法。贝叶斯推断、马尔可夫链和采样策略是MCMC算法的核心。

1.1 贝叶斯推断

贝叶斯推断是一种利用观测数据来修正先验假设的统计推断。它的理论基础是贝叶斯定理,

(|) =(|)()/()µ(|)(), (2)

式中:为观测数据;是对某1组未知参量的假设值, 本文中其为、、0、0四个自由参量;()为先验概率, 是在分析观测数据前认为参数值出现的概率;(|)为似然概率, 是模型参数值为时, 恰好能得到观测数据的可能性;(|)为后验概率, 表示在观测数据时, 模型参数值恰好为的概率;()为边缘概率, 是所有可能的参数取值下观测到数据的概率, 是一个常数。

后验概率可以理解为借助观测数据, 对先验概率进行修正后的概率。本文所做拟合的目的是希望得到模型参数的分布, 在实际使用过程中, 要先假设参数服从某种形式的概率分布函数(下文称为先验分布), 然后从中随机抽取参数值, 代入模型, 再计算似然概率。即可得到后验概率, 其与真正的后验概率存在一个常系数的差别。

为了得到每个参数的后验分布, 以及其中的最大后验值和参数可靠区间, 一种做法是在参数定义域内计算所有后验值。在模型复杂、参数维度高的场合, 这种做法将需要大量的计算资源, 因为每个参数的高概率分布区域可能落在相对比定义域小得多的范围内。一般的蒙特卡洛算法由于没有一个高效的搜索策略, 将会把大量的计算资源浪费在参数分布概率低的区域。为了解决这个问题, 人们提出对后验分布进行采样, 通过大量样本对后验分布进行近似。本文选择了MCMC算法, 它为多维分布的采样提供了一个高效率的方案。

1.2 马尔可夫链

对后验分布进行采样意味着不断地更新模型的参数值, 这可以看成状态的变化过程。一个随机过程中, 如果下一个状态的出现概率只取决于当前状态, 而与之前任一状态都无关, 即P(X+1=|1=1,2=2,×××,X=x) =P(X+1=|X=x), 那么这个随机过程就叫做马尔可夫链。

从当前状态过渡到下一个状态的概率可以由转移矩阵描述,, 其中任一元素p代表状态从变为的发生概率, 它其实是一个条件概率, 即在给定状态的前提下,状态出现的概率。因此, 转移概率矩阵描述了在状态空间中, 所有可能的状态变化的概率, 也包括一个状态之后出现相同状态的概率, 如11、22等。

马尔可夫链有一个特性, 只要满足每一个状态的出现概率都不小于0, 以及状态转换不存在周期性这2个条件, 无论这条链开始于哪一个状态点(0), 持续使用相同的转移矩阵, 经过一定次数()的状态转换后, 它的各种状态的分布将会收敛到一个稳定的分布——马尔可夫链的平稳分布(用表示), 且0×»。在满足Kolmogorov准则的情况下, 当马尔可夫链收敛到平稳分布后, 状态的转移将满足“细致平衡(Detailed balance)”条件[8], 即=。其中:π和π为处在和状态的平稳分布;为从状态转换到状态的马尔科夫链转移矩阵。

1.3 Metropolis-Hasting算法

在模型参数的拟合中, 虽然可以通过式(2)计算后验, 但无法直接对整个后验分布进行采样。这个问题可以通过把参数的后验分布设为马尔可夫链的平稳分布来解决。这样, 对后验的采样就转化成对收敛后的马尔科夫链的采样, 因此, 关键是如何使马尔可夫链收敛到平稳分布。Metropolis-Hasting算法正是利用了马尔可夫链的细致平衡特性, 通过寻找合适的转移矩阵来实现这一目的[9–10]。尽管一开始转移矩阵是未知的, 但是可以先假设一个, 再通过细致平衡进行修改。一个可行的方案是将假设参数的先验分布(·|)作为初始的转移矩阵。显然, 开始这个转移矩阵并不满足细致平衡条件, 例如可能出现(+1|) >+1(|+1), 该式可以解读为从状态转移到状态+ 1的概率比反过来转移的概率大。为了满足细致平衡, 必须引入一个因子(+1|)来减少从状态到状态+ 1的转换概率, 从而实现平衡, 即(+1|)(+1|) =+1(|+1)。因此可以得到(+1|) =+1(|+1)/(+1|), 其中(t+1|θ)称为接受概率, 用于判断是否将+ 1状态接受为一个新的状态, 还是要继续保留状态。在实际操作中, 若(t+1|θ) > 1, 就接受+ 1状态作为新的当前态。若(θ+1|θ) < 1, 则从均匀分布(0, 1)中产生一个随机值, 如果(θ+1|θ) >, 则接受+ 1状态, 否则保持当前状态。+ 1状态被接受后, 参数的先验分布也随之被修改。重复执行上述过程, 经过大量迭代, 产生参数的马尔可夫链最终收敛到平稳分布。此时对平稳分布进行采样相当于对后验分布进行采样。

假设被检测的后验分布是中值为5、标准差为1.5的高斯分布, 采用的初始先验是中值为50、标准差为0.5的高斯分布。经过2 000次迭代后, 先验被修正成中值为5.09, 标准差为1.54的高斯分布。图2给出了MCMC的参数轨迹历史, 从图2可以看出在第1000次随机过程之前, 先验一直在被修正。在1 000次之后, 参数值的变化已基本收敛, 马尔科夫链收敛到平稳分布, 即所求的后验分布, 那么收敛后的采样点即可用于后续的统计分析。

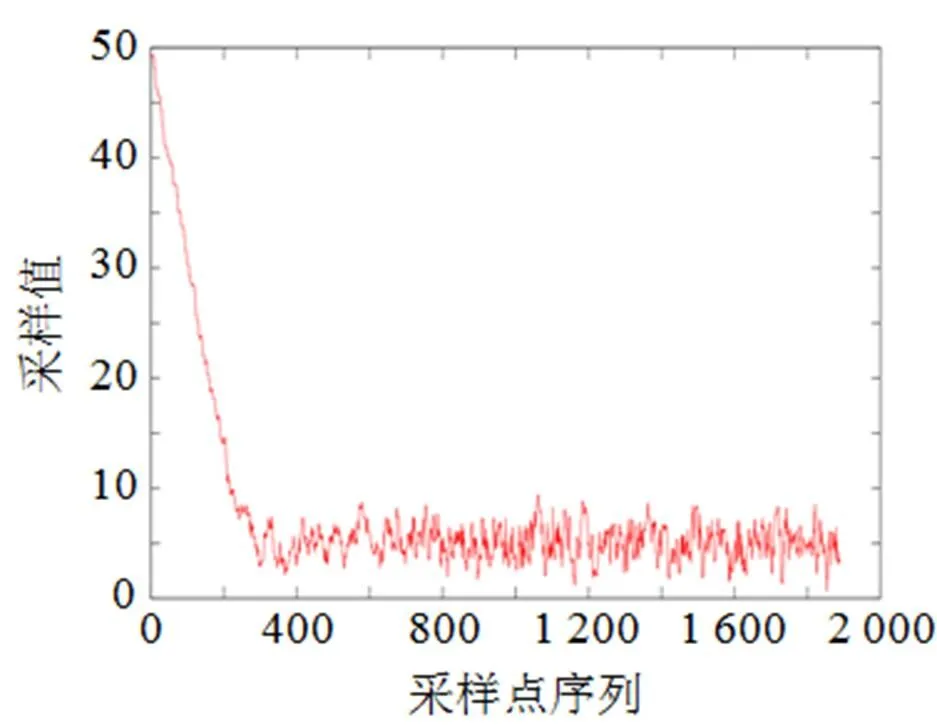
图2 马尔可夫链的参数序列

1.4 拟合步骤

给定一颗脉冲星, 本文使用RVM对该星若干脉冲相位的偏振位置角数据ψ、(= 1, 2, 3,×××,)进行拟合, 步骤如下。

(1) 为4个模型参数、、0和0指定初始的先验分布, 本文取高斯分布, 然后根据先验分布随机生成一组参数值θ(,,0,0)作为当前参数值。

(2) 把参数值θ代入似然概率表达式计算后验概率(θ|)。本文采用的似然概率表达式为, 其中mi是在相位上RVM模型预言的线偏振位置角, 可通过求解式(1)得到。

(3) 利用当前先验分布(·|θ), 从当前参数值θ生成新的参数值θ+1。

(4) 把参数值θ+1代入似然概率表达式, 计算后验概率(θ+1|)。

(6) 若> 1, 则接受+1为当前参数值, 即成为新的, 更新先验分布; 若< 1, 则从均匀分布(0, 1)产生一个随机值, 如果>, 则接受θ+1为当前参数值, 否则拒绝θ+1并保持θ。

(7) 重复步骤(3)～(6), 直至参数值变化收敛。

(8) 继续产生充分多的参数样本, 得到参数的统计分布, 确定其最高后验概率值对应的参数值, 以此作为参数的最可能取值, 并根据分布确定可信区间。

2 样本数据及结果

2.1 数据

为了与已有文献的方法进行对比, 检验MCMC方法的有效性, 本文选择了与文献[2]中相同的样本进行拟合, 共有10颗具有高质量观测数据的脉冲星。数据来自European Pulsar Network (EPN)脉冲星轮廓数据库, 与文献[2]一样, 所选的1418 MHz的数据均来源于Weisberg等[11]的观测。Everett等[2]指出, 由于观测噪声的影响, 由Stokes参量直接计算线偏振强度和线偏振位置角会带来偏差, 因此, 本文按照文献[2]的方法对线偏振位置角进行预处理, 修正偏差。

与文献[2]略有不同的是, 本文只保留了脉冲窗口中的线偏振位置角数据, 在窗口之外辐射极弱地方的线偏振位置角误差很大, 本文没有采用。与文献[2]相同的是, 针对少数脉冲星在一些相位段上的线偏振位置角完全偏离RVM模型曲线的情况, 在拟合时删除了这些数据, 这些星包括PSR J0826 + 2637、PSR J0953 + 0755、PSR J1543 + 0929和PSR J1932 + 1059。

2.2 参数拟合值和可信范围的确定

经过MCMC方法拟合后, RVM模型的每个参数都会有一系列采样值。去掉后验分布稳定前的采样, 对剩下的采样值做统计直方图并进行平滑, 可以得到参数的后验分布。将后验分布中出现概率最大处所对应的参数值作为最可能的参数取值, 在其左右某一范围内的参数区间作为某一可信度水平上的取值区间, 本文选用95%可信区间。以PSR J0528 + 2200为例, MCMC拟合得到的4个参数的后验分布如图3所示。其中统计直方图是大约使用了4 × 105个采样值得到的, 最可能的参数拟合值用概率密度最高处的竖线表示。对参数值的大小进行升序排序, 2.5%与97.5%两个分位点之间的取值区域作为该参数的95%可信区间, 对应于图3中左右两侧竖线之间的区间。图3中包络线为经过平滑得到的概率密度分布曲线。这2种方法给出结果的差别非常小。在PSR J0528 + 2200的拟合中, 从产生样本到输出所有被接受的样本一共耗时8.5 s。其它样本中, 最少耗时4.9 s, 最多耗时31.9 s, 平均耗时13.4 s。

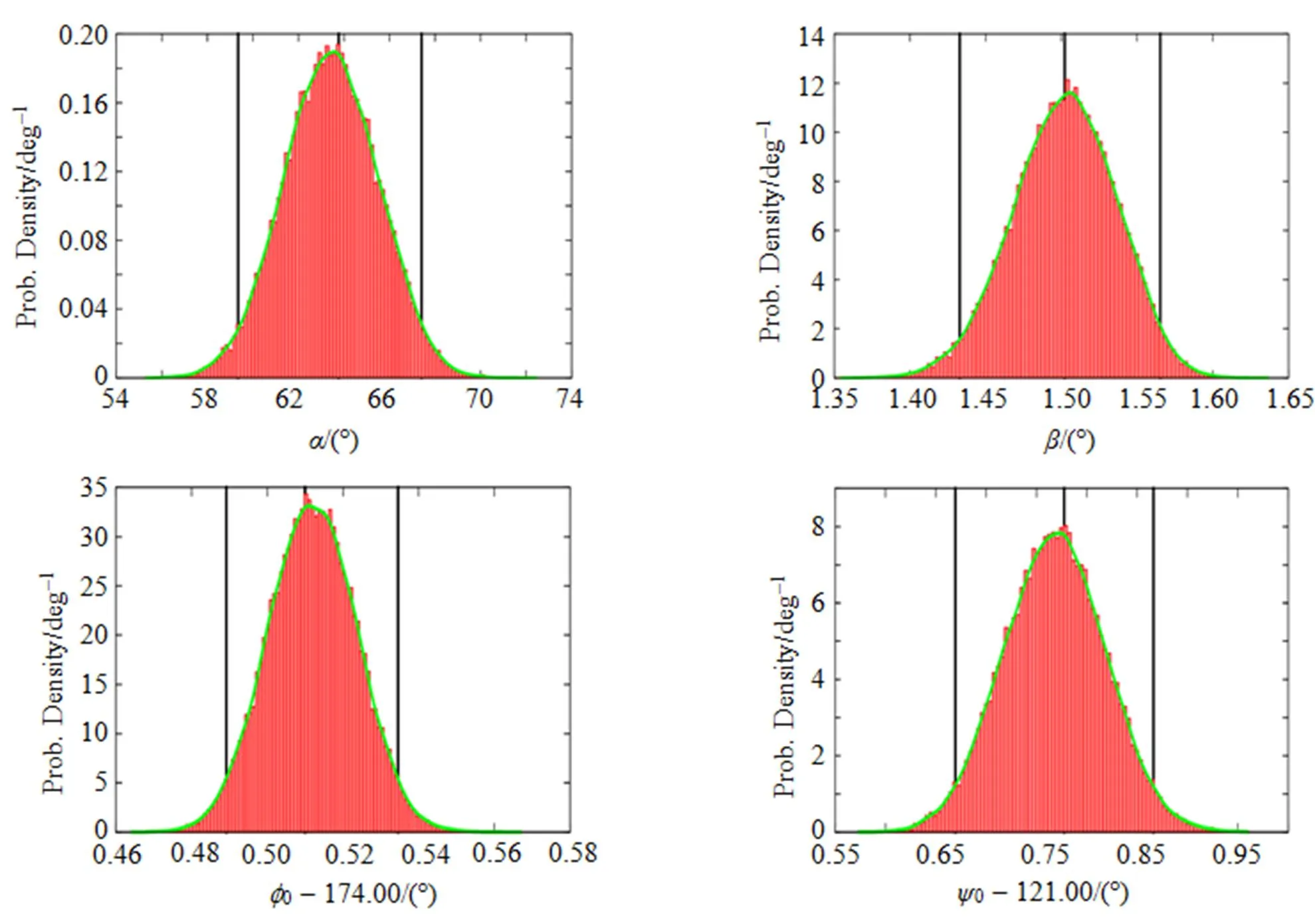
图3 PSR J0528 + 2200的RVM模型参数后验概率密度分布

2.3 拟合结果

本文使用MCMC算法成功地拟合了10颗脉冲星, 得到了模型参数的最可能取值和95%可信区间, 拟合结果见表1, 用4个参数的最可能值得到的拟合曲线见图4～7。为了方便对比, 文献[2]的拟合结果也分别在表1和图4～7中给出。由于文献[2]没有给出0的拟合值, 因此表1未列出该参数。图4中: 图4(a, b, c)为本文MCMC算法的拟合结果, 图4(d, e, f)为LM算法拟合结果[2]; 图4(a, d)为脉冲偏振轮廓, 曲线1为总强度, 曲线2为线偏振强度, 曲线3为圆偏振强度; 图4(b, e)为线偏振位置角数据和RVM模型的最佳拟合曲线; 图4(c, f)为拟合残差, 其计算方法为: 观测值减去拟合值, 再除以观测误差。图5、6、7中各分图说明与图4相同。

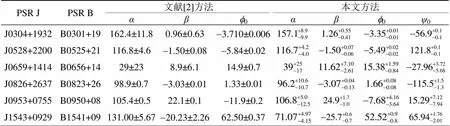
表1 2种方法拟合结果的比较/(°)

续表1

J1841+0912B1839+0986.1±11.42.30±0.040.34±0.02 J1917+1353B1915+1373.0±19.45.4±0.56.8±0.1 J1918+1444B1916+14118.0±33.4-1.00±0.330.38±0.01 J1932+1059B1929+1035.97±0.9525.55±0.87-19.6±0.2

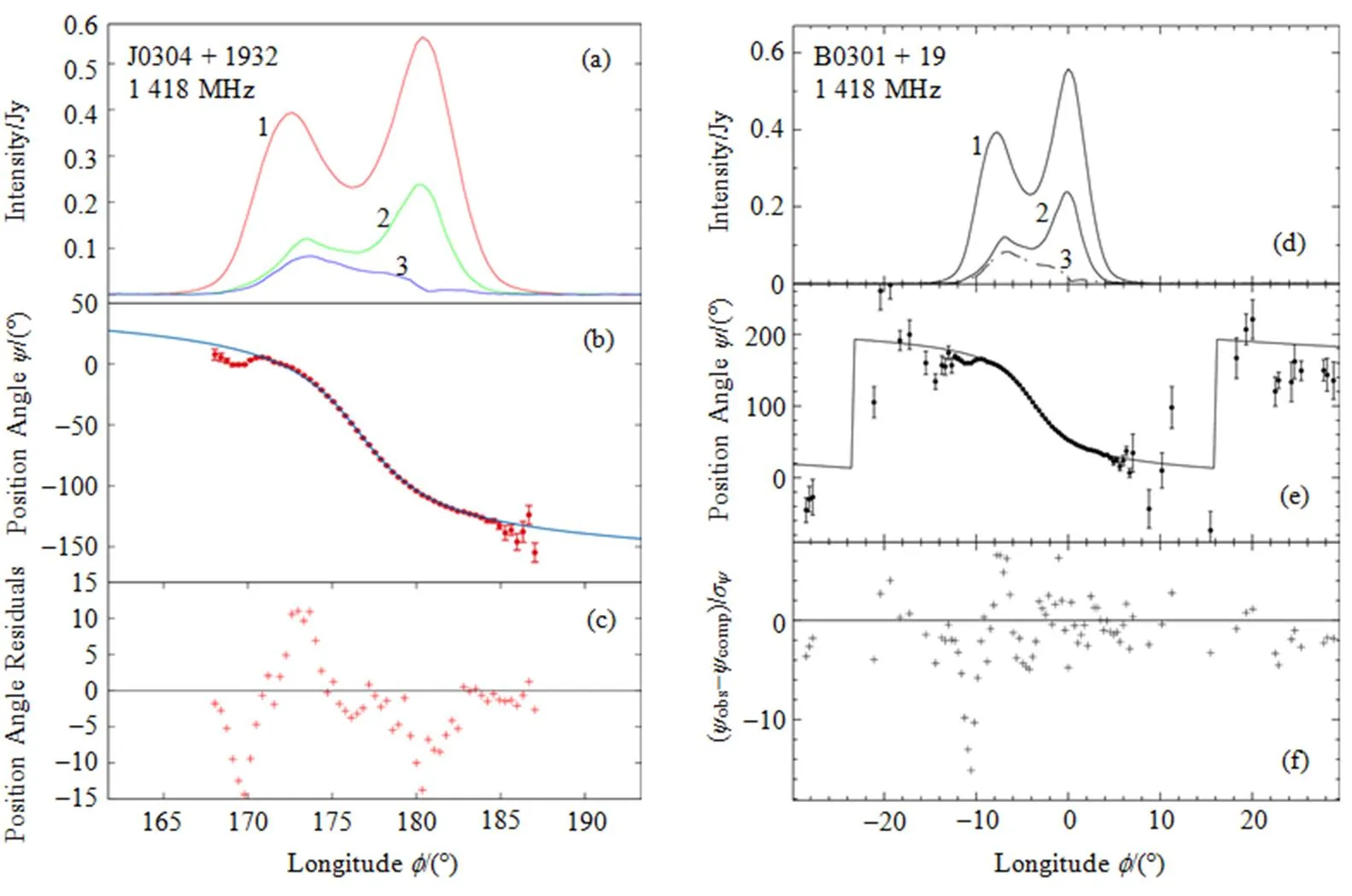
图4 PSR J0304 + 1932的RVM模型拟合曲线

图5 PSR J0528 + 2200的RVM模型拟合曲线

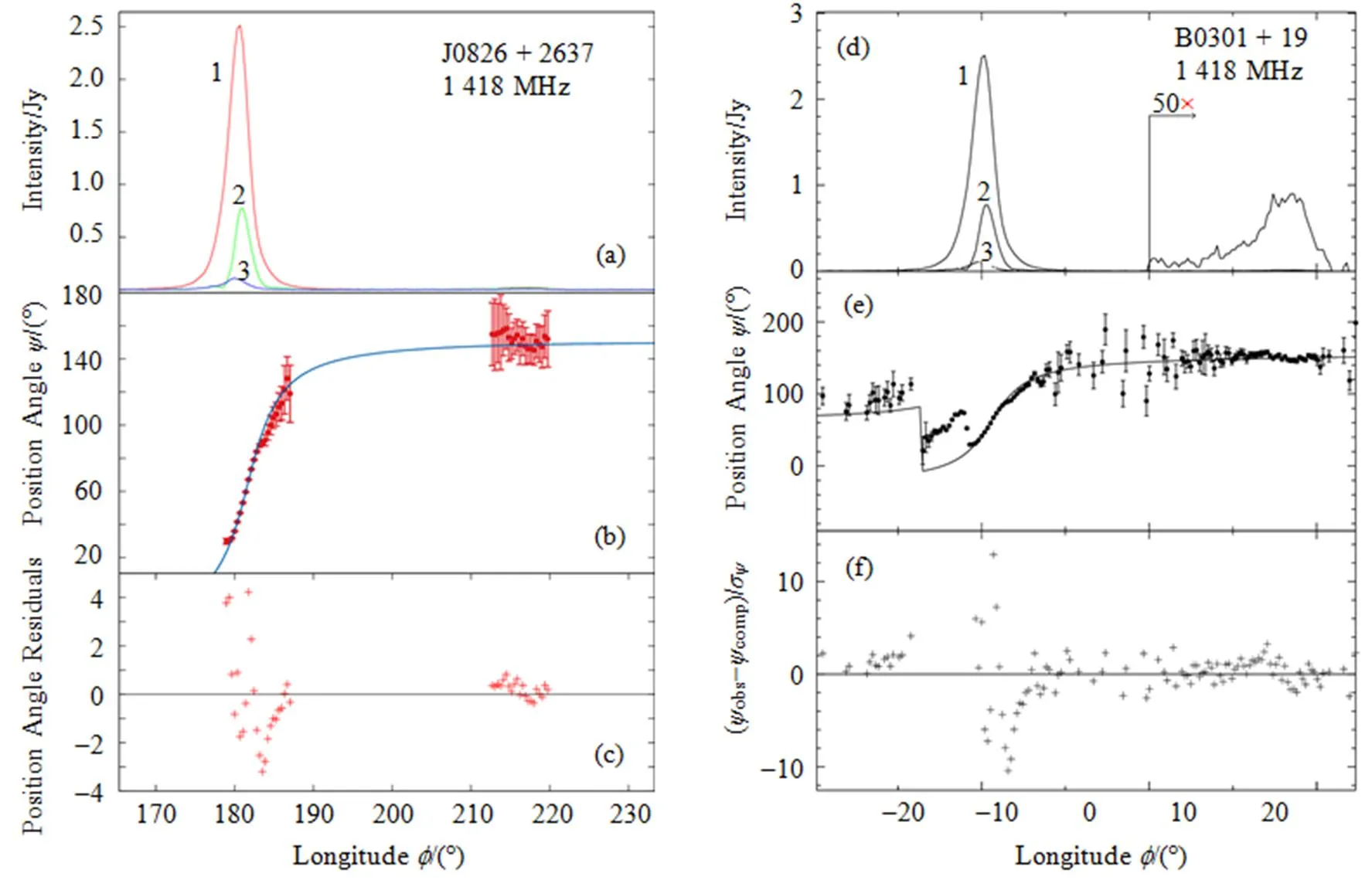
图6 PSR J0826 + 2637的RVM模型拟合曲线

图6(a, b, c)在相位(175°, 178.6°)范围内的线偏振位置角不满足RVM, 未用于拟合, 与文献[2]的处理相同。

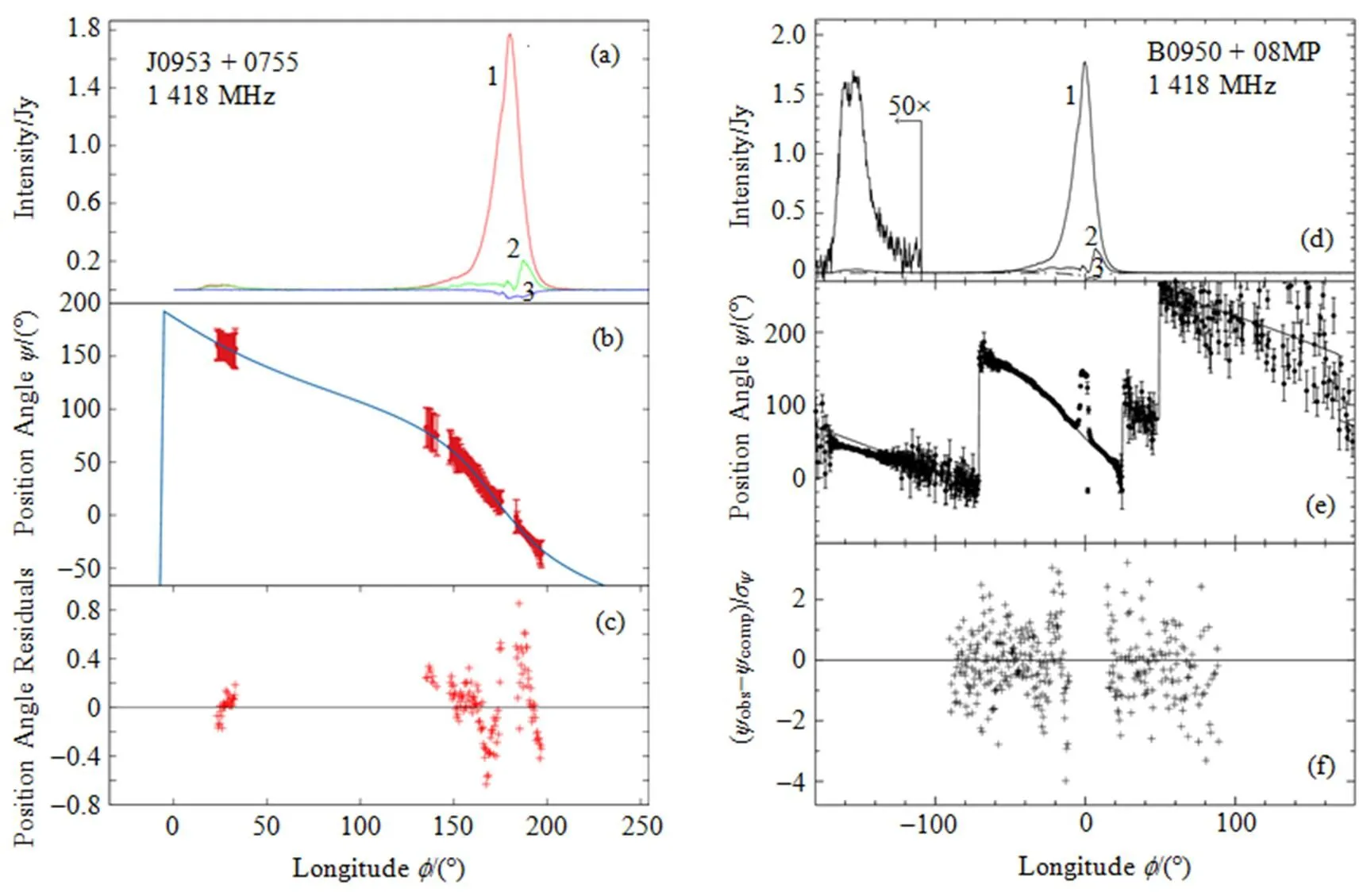
图7 PSR J0953 + 0755的RVM模型拟合曲线

图7(a, b, c)在相位(175.8°, 181.0°)范围内的线偏振位置角不满足RVM, 未用于拟合, 与文献[2]的处理相同。

从表1和图4～7可以看出, 本文方法得到的和与Everett等[2]的结果十分接近, 尤其是PSR J0304 + 1932、PSR J0528 + 2200、PSR J0826 + 2637、PSR J0953 + 0755、PSR J1917 + 1353和PSR J1918 + 1444这6颗星。LM方法仅给出了对称的不确定度, 而MCMC方法则能够给出非对称可信区间。

3 结论

本文首次将MCMC算法应用于脉冲星辐射几何限定的研究, 通过使用旋转矢量模型对脉冲星射电波段线偏振位置角的观测数据进行拟合, 得到了10颗脉冲星的磁倾角和碰撞角。与已有文献基于LM算法的拟合结果相比, 本文的结果与相关文献的结果高度一致, 证明了该方法的有效性。与LM算法和格点计算拟合方法相比, MCMC算法具有如下优点: (1) 对多维参数的拟合效率高; (2) 对参数的初始值不敏感, 能够较好地抑制过拟合; (3) 能够给出更为可靠的参数不确定度估计; (4) 相比格点计算, 参数拟合精度高。在磁倾角和碰撞角的拟合工作中, 效率和过拟合是2个主要的问题。本文研究显示MCMC方法在这2方面, 特别是效率方面有突出的优势, 为后续开展大样本的拟合工作提供了有力的工具。

致谢:感谢中国科学院高能所夏俊卿及北京大学李柯伽给予本工作的讨论。

[1] Radhakrishnan V, Cooke D J. Magnetic poles and the polarization structure of pulsar radiation [J]. ApL, 1969, 3: 225–229.

[2] Everett J E, Weisberg J, M. Emission beam geometry of selected pulsars derived from average pulse polarization data [J]. ApJ, 2001, 553: 341–357.

[3] Keith M J, Johnston S, Bailes M, et al. The high time resolution universe pulsar survey-IV. discovery and polarimetry of millisecond pulsars [J]. MNRAS, 2012, 419: 1 752–1 765.

[4] Rookyard S C, Weltevrede P, Johnston S. Constraints on viewing geometries from radio observations of γ-ray-loud pulsars using a novel method [J]. MNRAS, 2015, 446: 3 367–3 388.

[5] Marquardt D W. An algorithm for Least-Squares estimation of nonlinear parameters [J]. Journal of the Society for Industrial and Applied Mathematics, 1963, 11(2): 431–441.

[6] Wang H G, Pi F P, Zheng X P, et al. A Fan Beam Model for radio pulsars. I. observational evidence [J]. ApJ, 2014, 789: 73–102.

[7] Powell M. J. D. An efficient method for finding the minimum of a function of several variables without calculating derivatives [J]. Computer Journal, 1964, 7(2): 155–162.

[8] Boltzmann L. Lectures on gas theory [M]. Berkeley: U of California Press, 1964.

[9] Hastings W K. Monte Carlo sampling methods using Markov chains and their applications [J]. Biometrika, 1970, 57(1): 97–109.

[10] Chib S, Greenberg E. Understanding the Metropolis-Hastings Algorithm [J]. The American Statistician, 1995, 49(4): 327–335.

[11] Weisberg J M, Cordes J M, Lundgren S C, et al. Arecibo 1 418 MHz polarimetry of 98 pulsars: full stokes profiles and morphological classifications [J]. ApJS, 1999, 121: 171–217

(责任编校: 江河)

A bayesian approach to fitting the polarization position angle of pulsars

Chen Weiwei, Wang Hongguang, Zhang Yanrong

(School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China)

For pulsar emission beams, a widely used relationship between the polarization position angle (PPA) and the pulse phase is given by the Rotation Vector Model (RVM). Current methods of fitting the PPA with RVM are on the basis of Levenberg-Marquardt nonlinear fitting or grid searching algorithms, however, they suffer from inefficiency and overfitting problems. A Markov Chain Monte Carlo (MCMC) algorithm on the basis of Bayesian inference is developed and applied to the fitting of PPA for 10 pulsars, which have been studied in literature with old methods. It is shown that the MCMC algorithm can not only obtain consistent results as those in literatures, but also have advantages in efficiency, the abilities of overcoming over-fitting and estimating the uncertainties of model parameters.

pulsar; emission beam; polarization position angle; Rotating Vector Model

http://www.cnki.net/kcms/detail/43.1420.N.20160526.1115.002.html

10.3969/j.issn.1672–6146.2016.04.007

P 145.6

1672–6146(2016)04–0027–08

陈威威, anforone@msn.com;王洪光, hgwang@gzhu.edu.cn。

2016–05–20

国家自然科学基金(NSFC 11178001; 11573008)。