基于改进萤火虫算法的分布式电源优化配置

陈海东，庄 平，夏建矿，代文章，逯 洋，高 奇，陈 涛



基于改进萤火虫算法的分布式电源优化配置

陈海东，庄 平，夏建矿，代文章，逯 洋，高 奇，陈 涛

(国网宁夏电力公司石嘴山供电公司，宁夏 石嘴山 753000)

在分析分布式电源特性的基础上，建立了含分布式电源的购电成本最小、网损费用最小、投资成本最小以及电压稳定裕度最大的多目标优化模型，能够比较实际、科学地反映DG规划布局。在此基础上，应用超效率数据包分析评价方法，明确各目标函数的权重组合方案，将DG多目标规划问题转换成单目标规划问题。鉴于传统萤火虫算法具有容易早熟、过度依赖控制参数的缺陷，将混沌搜索策略和全局思想融入到萤火虫算法，提出了一种改进型萤火虫算法；并将其应用于解决分布式电源的规划问题。通过算例验证所提算法具有良好的实用性和适应性，并且也验证了所提模型的实际意义。

分布式电源；多目标优化；改进萤火虫算法；超效率数据包；混沌理论

0 引言

分布式发电作为智能电网的重要组成部分，近年来受到日益广泛的关注[1]。分布式电源接入配电网后，引起各支路潮流大小和方向改变，使系统损耗不仅与负荷大小有关，还与DG选址及定容有关。因此，深入研究DG的合理规划具有重要意义[2-5]。

目前，国内外学者已对DG的优化配置问题进行了较多研究。文献[6]采用蚁群算法确定DG的最佳安装位置与容量大小，但蚁群算法要求各调节参数必须选择合理，否则会影响其优化效果。文献[7]提出多目标量子遗传优化算法应用到分布式电源选址和定容问题的求解中，建立了降低DG投资和运行成本、减少系统有功网损的优化模型，但是这种算法的参数设置复杂，并且运行速度慢。文献[8]提出一种改进型PSO算法，应用在含风电场的以有功网损最小为目标函数的优化模型，但是这种改进算法一般计算时间较长、运行复杂。文献[9]研究分布式电源多目标优化模型，利用线性加权法将多目标函数转化为单目标优化问题，但是这种方法必须统一量纲，由于缺乏经验会造成目标函数难以转化。文献[10]将超效率DEA应用在电力公司效率评价，通过对中国8个省份的电力公司的综合效益评价，提出了多种改革方案，并且通过算例验证了DEA效率评价的可靠性。文献[11]提出超效率DEA的优化组合与帕累托优劣解的相似性，将两种方法应用在工厂生产线流动组合上，通过算例验证了超效率DEA的实用性。文献[12]以网损为目标函数，提出采用常规萤火虫算法(Firefly Algorithm, FA)求解该问题，但基本FA算法收敛速度较慢，且解的质量不高。文献[13]提出萤火虫算法在分布式电源定容和选址的应用，通过与遗传算法的比较，验证该算法收敛速度较快。

本文所建立的目标函数不仅兼顾配电网运营商的利益，目标函数中还加入了用户购电成本以及系统电压稳定，并且应用DEA将多目标规划问题转化为单目标，在此基础上，提出了一种改进型的萤火虫算法，并将此算法应用在分布式电源的规划问题。

1  分布式电源规划的数学模型

1.1   数学模型的建立

首先建立含DG的配电网规划配置模型，在满足节点电压、线路极限传输功率、电流约束条件的同时，获得最大的效益。

1) 用户的购电成本

2) 分布式电源的投资成本

3) 网损费用

以牛顿拉夫逊潮流公式为基本，结合分布式电源的节点注入功率，给出网损计算公式为

分布式电源接入配电网之后系统的网损和分布式电源安装节点相应的有功和无功功率注入容量有关，如式(5)、式(6)所示。

将式(5)和式(6)代入到式(3)和式(4)，得到接入分布式电源之后的系统有功网损为

将配电网网络损耗转化为经济指标，如式(8)。

4) 电压稳定裕度最大

、支路电压稳定裕度的计算公式如式(9)。

1.2相关模型的约束条件

(1) 节点功率平衡约束

(2) 节点电压约束

(3) 输电线路的极限传输功率约束为

(4) DG安装总容量限制

2 多目标函数权重系数的确定

超效率DEA是一种适应于多投入多产出的决策单元相对效率，数据包络分析(即DEA)可以看作是一种统计分析的新方法。它是根据一组关于输入－输出的观察值来估计有效生产前沿面的[14]。

对电压稳定裕度、综合投资成本、网损费用、购电成本做归一化处理，即：，，，。因为超效率输出变量的值必须是最大值，所以本文将电压稳定裕度作为决策单元的输出量[15]。EK代表产出决策变量的效率，根据DEA特性，拥有最高效率的决策变量，其他决策单元更为有效，即在相同输入变量的投入下，该决策变量具有更高效率的输出产量。因为本文的多目标函数综合费用最低，在归一化处理的时候，将运行费用最大化处理，得到的最高效率的线性权重系数为。因此采用线性加权转化得到的单目标函数表达式为

3  萤火虫算法

3.1 萤火虫算法的优化机理

萤火虫算法由剑桥学者Yang Xin-she等[16]在2008年提出，通过模拟自然界萤火虫的群体行为来实现优化。

在算法的优化过程中，主要有两种因素决定了萤火虫的相互吸引，即它们的亮度和吸引度。在这里将萤火虫个体相互吸引和移动的过程转化为目标函数的优化和求解过程。萤火虫个体会被随机地分布到目标函数的求解空间，而萤火虫自身的亮度越亮表明目标函数所处的空间位置越优越。萤火虫的吸引度与其亮度密切相关，亮度较亮的萤火虫个体拥有更强的吸引度。在相互吸引的过程中，萤火虫的亮度会随着空间距离的增加和传播介质的吸收而逐渐减少。在每一次的迭代中，萤火虫的位置在不断地更新，而每一次位置的更新中，问题的求解也在进一步地优化。

3.2 算法的数学描述与分析

萤火虫的移动方向和移动距离主要由它的亮度和吸引度决定。从数学角度对萤火虫算法优化过程描述如下。

定义1 萤火虫的相对荧光亮度为

定义2 萤火虫的吸引度为

3.3 对FA算法进行改进

3.3.1引入混沌理论

混沌运动貌似是一种随机的运动，但是却隐含着极其精致的内在结构，并且能够在一定的范围内以其自身所具有的规律不重复地遍历所有的状态，利用混沌变量进行优化搜索会比盲目无序地随机搜索更具有优越性。混沌具有遍历性的特点，使其可以作为搜索过程中避免陷入局部极小值的一种优化机制[17]。从式(16)~式(18)可以看出，萤火虫的参数对于算法寻优起到很重要的决定作用，如果能够使算法的参数在可行域内随机变化，能够达到提高算法的全局寻优能力。本文采用Logistic映射函数对萤火虫算法参数进行控制调整，改进之后的萤火虫更新公式为

3.3.2引入全局最优思想

从萤火虫的更新位置公式(18)可以发现，每只萤火虫都会向解空间内亮度比它强的萤火虫移动。此时萤火虫的寻优只与周围的萤火虫的亮度有关，这里忽略了全局最优值[18]。对于标准萤火虫算法，在每次迭代中较亮的萤火虫个体(局部最优)会对其他萤火虫发挥其影响力，最大化地吸引它们向自己移动。为克服标准FA算法的缺陷，提高萤火虫的寻优能力，本文在萤火虫的移动过程中引入全局最优的思想。

在改进的萤火虫算法中，使用笛卡尔距离来计算其他萤火虫与当前处于全局最优萤火虫位置的距离，计算公式如式(22)、式(23)。

3.4 算法步骤

运用改进萤火虫算法求解分布式电源选址和定容问题的步骤如下。

步骤1：初始化符合约束条件的萤火虫位置和算法相关参数值。

步骤2：分别以上述4个目标函数中的每一个作为单个目标函数，不考虑另外3个目标函数，求取这3种情况下的最优解。

步骤3：采用伪随机数发生器产生的一组权重向量，把多目标优化问题转化为单目标问题。

步骤4：把求得的优化变量值代入4个目标函数中，得到4个目标值。采用超效率DEA方法进行评价，将3个最小化目标值作为决策单元的输入，将一个最大化目标值作为决策单元的输出；根据最终评价结果从一组权重向量中选出一个最有效的权重向量作为各目标的最终权重系数。

步骤5：采用改进萤火虫算法进行求解。

4  算例分析

4.1 算例主要参数

本文以IEEE-69(如图1所示)节点配电网系统为例，将各分布式电源看作负的PQ节点处理，功率因数取0.9。首先，令，如果求解出为0，表明在负荷节点处不安装分布式电源；若为非零常数，其安装容量为，其中的取值范围为[0,]之间的实数，编号对应的最大值，单位网损电价=0.65元/kWh，系统年运行时间为8 760 h，分布式发电单位安装费，运行维护成本。为0.067，规划年限为20年。

图1 IEEE-69节点配电网测试系统图

4.2 算例结果分析

本文选取36组权重系数，每一次变化0.1，权重系数的变化范围为0.1~0.8，采用线性加权的方法把多目标优化问题转化为单目标优化问题，利用改进萤火虫算法求解转化后的单目标优化问题。超效率DEA方法对于评价36组权重系数组合方案进行评价，明确DEA值最高的为最有效的组合方案。

从表1可以看出，在决策单元9和22权重系数组合方案下的超效率DEA评价值都大于1，并且决策单元9的相对效率更高，故采用决策单元9所对应的组合方案0.2、0.1、0.1、0.6分别作为各目标函数的权重系数，表2是在满足各种约束条件以单元9为权重系数，应用本文算法得到的优化结果。

从表2可以得出，采用改进FA算法DG接入后系统网损由原来的224.94 kW减少到135.62 kW，优化后的有功网损下降率为44.58%，有效地降低了投资费用，而应用FA算法和PSO算法系统网损分别减少了40.03%和37.36%，均小于改进FA求解结果。另外分布式电源接入之后，有效地降低了电网的购电成本。

表1几组典型权重系数的组合评价值

Table 1 Combinational evaluation results of typical weight coefficient

表 2三种算法运行结果对比

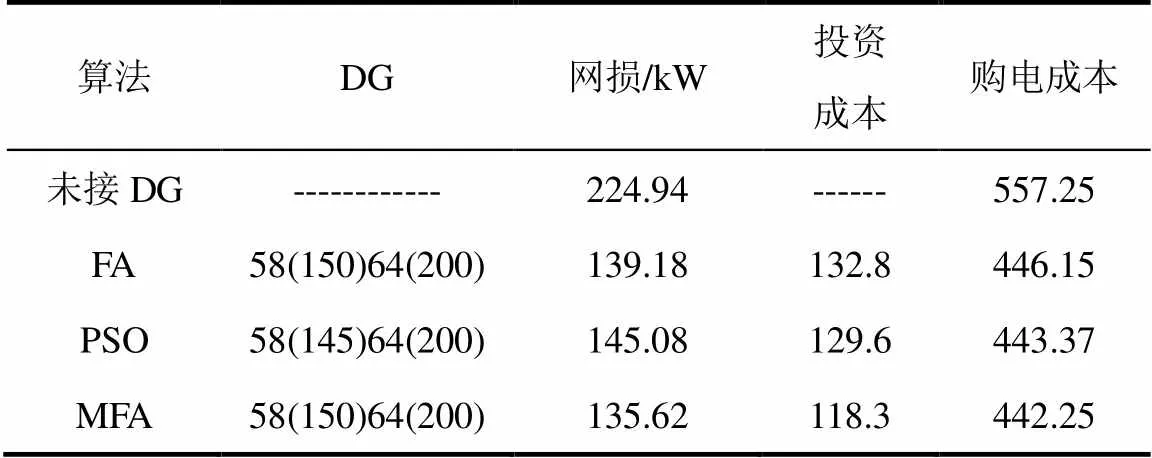
Table 2 Running results with three algorithms

图2是在接入DG前后，采用本文算法对分布式电源进行规划，节点电压的最低值均得到了提高，优化之后最低电压为0.968 1 p.u.，配网系统电压普遍有明显改善，平均电压为0.993 1 p.u.，提高了系统节点整体电压水平。

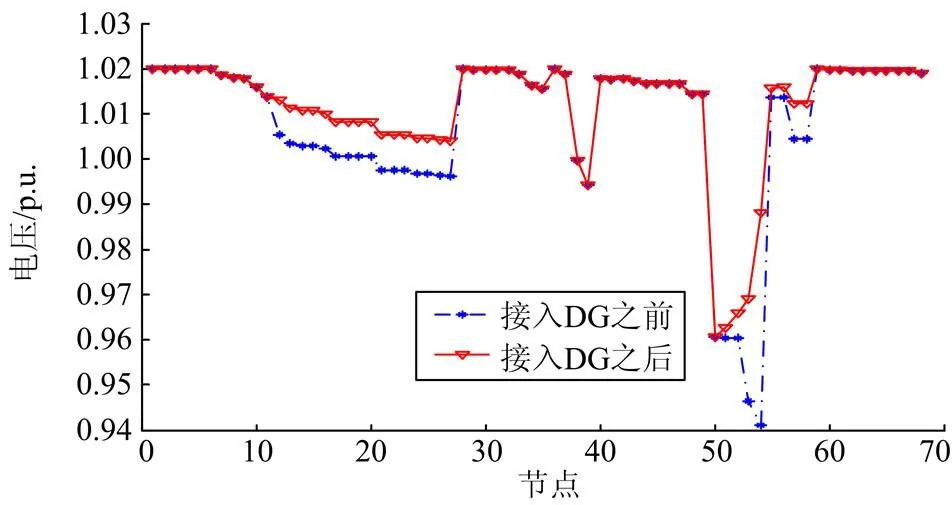
图2 IEEE-69各节点电压幅值

图3为采用改进萤火虫算法、基本萤火虫算法和PSO对目标函数进行的独立优化20次的最优情况下的收敛特性曲线。从图3可以看出，粒子群算法和基本萤火虫算法，收敛速度较慢，并且容易陷入局部最小值，且搜索精度不高，改进萤火虫不仅引入了全局最优值和混沌搜索策略，能够找到更高质量的优化解，并且收敛速度和精度比较优越。

图3三种算法收敛曲线图比较

5 结论

1) 本文首先建立分布式电源多目标优化模型。然后在此基础上，应用超效率数据包对多目标函数进行评价，在满足相关约束条件下，把多目标优化问题转化为单目标问题求解。算例结果表明，分布式电源合理配置能够减少系统网损以及提高系统的稳定性，同时验证该优化模型具有一定的实际意义。

2) 提出改进的萤火虫算法，该算法引入混沌理论，对萤火虫算法的参数进行混沌搜索，引进全局最优的思想，能够提高算法收敛精度，最后通过算例验证所提算法具有较好的适应性。

[1] 唐志军, 邹贵彬, 高厚磊, 等. 含分布式电源的智能配电网保护控制方案[J]. 电力系统保护与控制, 2014, 40(8): 9-14.

TANG Zhijun, ZOU Guibin, GAO Houlei, et al. Protection control scheme of the distributed power supply with DG[J]. Power System Protection and Control, 2014, 40(8): 9-14.

[2] 张勇军, 苏杰和, 羿应棋. 基于区间算术的含分布式电源电网无功优化方法[J]. 电力系统保护与控制, 2014, 42(15): 21-26.

ZHANG Yongjun, SU Jiehe, YI Yingqi. Reactive power optimization based on interval arithmetic with distributed power grid[J]. Power System Protection and Control, 2014, 42(15): 21-26.

[3] 吴万禄, 韦钢, 谢丽蓉, 等. 含分布式电源与充电站的配电网协调规划[J]. 电力系统保护与控制, 2014, 42(15): 65-73.

WU Wanlu, WEI Gang, XIE Lirong, et al. Coordinated planning of distribution network containing charging station and distributed generation[J]. Power System Protection and Control, 2014, 42(15): 65-73.

[4] 王威, 黄大为. 含可调度分布式电源的配电网综合优化[J]. 电工技术学报, 2015, 30(12): 429-433.

WANG Wei, HUANG Dawei. The coordination optimization of distribution networks with dispatched distributed generators[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 429-433.

[5] 韩璐, 李凤婷, 周二雄, 等. 基于成本-收益的微网分布式能源优化配置[J]. 电工技术学报, 2015, 30(14): 388-396.

HAN Lu, LI Fengting, ZHOU Erxiong, et al. The distributed energy optimization configuration of micro- grid based on cost-benefit[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 388-396.

[6] 赵金利, 于莹莹, 李鹏, 等. 一种基于锥优化的 DG 优化配置快速计算方法[J]. 电工技术学报, 2014, 29(12): 173-179.

ZHAO Jinli, YU Yingying, LI Peng, et al. A fast determination method of DG capacity in distribution network based on conic programming[J]. Transactions of China Electrotechnical Society, 2014, 29(12): 173-179.

[7] 王瑞琪, 李珂, 张承慧, 等. 基于多目标混沌量子遗传算法的分布式电源规划[J]. 电网技术, 2011, 35(12): 183-189.

WANG Ruiqi, LI Ke, ZHANG Chenghui, et al. Distributed generation planning based on multi-objective chaotic quantum genetic algorithm[J]. Power System Technology, 2011, 35(12): 183-189.

[8] 姜文, 严正. 基于一种改进粒子群算法的含风电场电力系统动态经济调度[J]. 电力系统保护与控制, 2010, 38(21): 173-178, 183.

JIANG Wen, YAN Zheng. Dynamic economic dispatch considering wind power penetration based on IPSO[J]. Power System Protection and Control, 2010, 38(21): 173-178, 183.

[9] LI Ming. A novel swarm intelligence optimization inspired by evolution process of a bacterial colony[C] // Proceedings of the 10th World Congress on Intelligent Control and Automation, Beijing, China,2012,25(5): 112-117.

[10] 王金祥, 吴育华. 基于超效率DEA 模型的电力公司效率评价[J]. 东北电力学院学报(自然科学版), 2004, 24(4): 22-25.

WANG Jinxiang, WU Yuhua. Research on efficientevaluation of electric power companies based onsuper- efficiency DEA model[J]. Journal of NortheastChina Institute of Electric Power Engineering (Natural Science Edition), 2004, 24(4): 22-25.

[11] 楼旭明, 窦彩兰, 汪贵浦. 基于DEA的中国电力改革绩效相对有效性评价[J]. 当代财经, 2006(4): 90-93.

LOU Xuming, DOU Cailan, WANG Guifu. Chinese electric power reform performance relative validity evaluation based on DEA[J]. Contemporary Finance & Economics, 2006(4): 90-93.

[12] SULAIMAN M H, MUSTAFA M W, AZMI A, et al. Optimal allocation and sizing of distributed generation in distribution system via firefly algorithm[C] // 2012 IEEE International Power Engineering and Optimization Conference, Melaka, Malaysia, 2012: 84-89.

[13] HERBADJI O, NADHIR K, SLIMANI L, et al. Optimal power flow with emission controlled using firefly algorithm[C] // Modeling, Simulation and Applied Optimization (ICMSAO), 2013 5th International Conference on, April 28-30, 2013, Hammamet: 1-6.

[14] 魏权龄. 数据包络分析[M]. 北京: 科学出版社, 2004.

[15] 华瑶, 袁宏波, 于海龙. 基于DEA 的火电上市公司业绩分析[J]. 经济视角, 2008(12): 28-30.

HUA Yao, YUAN Hongbo, YU Hailong. The evaluation of the listed thermal power enterprises based on data envolopment analysis[J]. Economic Vision, 2008(12): 28-30.

[16] 阮仁俊, 陈烨, 刘天琪. 基于混沌理论和排序选择的蚁群无功优化算法[J]. 电网技术, 2009, 33(11): 49-54.

RUAN Renjun, CHEN Ye, LIU Tianqi. Ant colony algorithm based on chaos theory and ranking selection in reactive power optimization[J]. Power System Technology, 2009, 33(11): 49-54.

[17] YANG Xinshe, DEB S. Eagle strategy using levy walk and firely algorithms for stochastic optimization[J]. Study in Computational Intelligence, 2010, 284: 101-111.

[18] YANG X S. Firefly algorithms for multimodal optimization[C] // Stochastic Algorithms: Foundation and Applications, SAGA, 2009, 5792: 169-178.

(编辑 魏小丽)

Optimal power flow of distribution network with distributed generation based on modified firefly algorithm

CHEN Haidong, ZHUANG Ping, XIA Jiankuang, DAI Wenzhang, LU Yang, GAO Qi, CHEN Tao

(Shizhuishan Power Supply Company, State Grid Ningxia Electric Power Company, Shizuishan 753000, China)

Based on the detailed analysis on peculiarity of DG, this paper establishes a multi-objective optimal model with DG by minimizing the electricity purchase costs, power loss and investment costs and maximizing voltage stability margin, which can reflect the DG planning layout practically and scientifically. On the basis, the super-efficiency data envelopment analysis is employed to determine the appropriate weights among the three objective functions, and in this way the multi-objective optimization problem is transformed into a single-objective programming one. In terms of the defects of traditional firefly algorithm, which is easily premature, has slow speed of convergence, and excessively relys on control parameters, this paper proposes a modified firefly method by introducing chaos search strategy and overall thought into firefly algorithm and applies it to solve the DG planning problem. Finally, the practicality and adaptibility of the proposed algorithm are illustrated by experiments.

DG; multi-objective optimization; modified firefly algorithm;super-efficiency data envelopment analysis;chaos theory

TM614

1674-3415(2016)01-0149-06

2015-03-09；

2015-06-29

陈海东(1986-)，男，工学硕士，研究方向为分布式电源的优化调度。E-mail: 15111023604@163.com