三螺杆挤出机端面二维流场混沌混合拉格朗日拟序结构分析
佟莹,朱向哲,高鹤,何延东
三螺杆挤出机端面二维流场混沌混合拉格朗日拟序结构分析
佟莹,朱向哲,高鹤,何延东
(辽宁石油化工大学机械工程学院,辽宁抚顺 113001)
三螺杆挤出机是一种新型的聚合物流体加工设备,其独有的中心区呈现出几何结构和受力状态的周期性变化,混合机理非常复杂。区别于传统的线性混合分析,从拉格朗日体系的新视角对三螺杆挤出机混沌混合进行拉格朗日拟序结构分析,利用有限时间Lyapunov指数(FTLE)、拉格朗日拟序结构(LCS),结合Poincaré截面和粒子可视化技术研究三螺杆挤出机二维流场的流体输运和混沌混合机理,讨论了中心区动态结构特性对FTLE和LCS分布的影响,并与单螺杆挤出机和双螺杆挤出机进行了对比分析。结果表明,LCS将三螺杆挤出机流域划分为近螺杆区、远螺杆区和中心区3个具有不同运动特性的区域,扭结是连接近螺杆区、远螺杆区和中心区物质交换的桥梁。随着混合时间的增加,扭结的弯曲和折叠程度逐渐增大,增强了3个区域的物质交换,强化了三螺杆流场的混沌混合。三螺杆挤出机啮合区附近存在3个双曲固定点,混合能力较好。Poincaré截面中椭圆周期点的出现说明在流域中心有非混沌区存在,因此三螺杆挤出机的中心区混合能力相对较弱。
三螺杆挤出机;有限时间Lyapunov指数;拉格朗日拟序结构;混沌混合;流动;计算流体力学;数值分析
引 言
三螺杆挤出机是在传统的双螺杆挤出机基础上研发的一种新型高效聚合物加工设备,具有啮合区数量多、挤压面积大、混合效果好等优点。三螺杆挤出机比双螺杆挤出机增加了两个啮合区和一个中心区,几何结构更加复杂。特别是三螺杆挤出机独有的中心区,呈现几何面积由大到小的周期性变化,其中心区的物料也呈现“拉伸-压缩-折叠”的周期性受力状态。三螺杆挤出机内流体的流动和混合机理特别是中心区的动态循环特性对整个三螺杆挤出机流动和混合机理的影响一直是研究的热点和难点,也是研发新型高效螺杆挤出设备的关键。
目前,国内外对于螺杆加工流体混合机理的研究主要集中在分布混合和分散表征。Connelly等[1]采用粒子簇分布指数、分离尺度、平均混合效率和瞬时混合效率等参数表征二维混合器的分布混合,采用剪切应力和混合指数表征分散混合。Zhang等[2]采用停留时间分布(residence time distribution,RTD)表征聚合物流体分布混合。Domingues 等[3]采用Shannon熵和分布混合指数表征聚合物分布混合,采用毛细管数和液滴尺寸变形量表征分散混合强度。Nakayama[4]采用流体经历的平均应力和最大应力值衡量分散混合。在三螺杆流体方面,胡冬冬等[5]建立了三螺杆挤出机啮合块元件的三维等温流动有限元模型,利用Polyflow软件分析了三螺杆啮合块元件的物料流动和混合规律。Jiang等[6]采用有限元数值模拟和实验相结合,验证了三螺杆挤出机中炭黑加工的高效物料输运能力和强烈剪切效率。Miao等[7]研究了三螺杆挤出机螺纹元件的温度和能耗分布,分析了螺杆几何参数对三螺杆挤出机温度分布和能耗的影响。Wang等[8]采用混合指数、分离尺度、平均时间混合效率、瞬时混合效率、最大拉伸率和剪切速率等对三螺杆挤出机二维流场的分布混合和分散进行表征,并与双螺杆挤出机进行了比较。目前,聚合物流体线性混合的表征方法已具有相对较高的成熟度,但很难从本质上揭示三螺杆挤出机的复杂混合机理,因此分析结果存在一定的局限性。
混沌混合是强化聚合物加工流体层流混合的有效方法,传统混沌混合动力学主要以Poincaré截面和Lyapunov指数等为研究工具。Lee等[9]采用Poincaré截面和修正的Lyaponuv指数对单螺杆挤出机混沌螺杆螺槽展开模型进行了混沌混合研究。Hwang等[10]利用体积输运原理,采用Poincaré截面和粒子轨迹追踪,研究了销钉单螺杆挤出机折叠结构和混沌混合过程。徐百平等[11]对副螺棱轴向往复运动的单螺杆挤出机牛顿流体三维周期性流动和混沌混合进行了数值模拟,采用4阶Runge-Kutta方法实现流体追踪,采用Poincaré 截面揭示混沌混合区域。程志飞等[12]采用Poincaré截面和Lyapunov指数对Roller转子密炼机聚合物流体的混沌混合特性进行了研究。
近年来,在传统欧拉体系流动分析的基础上提出了基于拉格朗日体系的流动结构分析方法[13-15]。Haller等[16]利用有限时间Lyapunov指数(finite-time Lyapunov exponent,FTLE)定义了拉格朗日拟序结构(Lagrangian coherent structure,LCS)。Shadden等[17]进一步给出了LCS的精确定义,并证明了LCS与输运边界之间的关联性。Santitissadeekorn等[18]使用FTLE研究了单转子混合器内混沌混合机理,成功辨识了流场的LCS。Robinson等[19]采用光滑粒子流体动力学(smoothed particle hydrodynamics,SPH)方法计算了Cam转子密炼机二维流体的FTLE和LCS,研究了转子构型对LCS的影响。近期,拟序结构研究已有很大进展[15],使用拉格朗日方法分析二维流体混沌混合趋于成熟。
基于传统欧拉方法的螺杆挤出机二维流场的可视化研究虽然可以直观地了解聚合物流体的流动规律和粒子的运动轨迹,一定程度上有助于理解聚合物流体的混合规律,但难以刻画出螺杆流场中促进和抑制流体输运的局部区域和边界,很难捕捉到螺杆流场潜在的力学和几何学特性。目前,使用LCS分析聚合物加工的研究十分有限,尤其对三螺杆挤出机内流体混合的研究,未见基于LCS的三螺杆挤出机混沌混合分析的研究报道。本工作在三螺杆挤出机二维流场计算的基础上,应用拉格朗日方法拟序结构的分析方法,采用Matlab软件计算出流场的FTLE和LCS,并结合Poincaré截面和粒子可视化技术揭示三螺杆挤出机内流体在二维流场中的输运和混沌混合机理,讨论中心区动态结构特性对FTLE和LCS分布的影响,分析三螺杆挤出机二维流场的潜在动力学和几何特性,在此基础上从拉格朗日拟序结构分析视角对比研究单螺杆、双螺杆和三螺杆挤出机输运和混合机理的异同,为螺杆挤出机设计提供新的理论参考。
1 拉格朗日拟序结构
对于二维流场,其瞬时变化的速度场可表示为
式(3)说明流体粒子(流体质点)沿轨迹同时存在一个方向的拉伸和另一个方向的压缩。这种依赖时间速度场的轨迹就是双曲轨迹。其中,的谱范数代表有限时间Cauchy-Green张量的最大拉伸值,可表示为
由FTLE的定义可知FTLE表征相邻流体粒子的运动状态,定义其“脊”结构为拉格朗日拟序结构(LCS)。当积分时间向前时(>0),FTLE值越大,表明在该位置的物质被拉伸得越长,此时“脊”结构代表稳定流型,成为排斥的LCS;相反,当积分时间向后时(<0),表明该处物质将被压缩,此时“脊”结构代表非稳定流型,成为吸引的LCS。基于FTLE的LCS是分析非定常流体的有利工具,可以捕捉到流场潜在的力学和几何特性。
2 物理模型
同向啮合三螺杆挤出机的三根螺杆呈正三角形排列,具有3个啮合区和1个动态中心区,几何模型如图1(a)所示。其几何尺寸如下:螺杆根径13 mm,外径17 mm,机筒内径18.5mm,两螺杆中心距33 mm。使用Gambit软件进行几何建模,采用Polyflow软件中的网格重叠技术(mesh superposition technique,MST)。为捕捉流场中螺杆与筒壁间隙中流体的运动,螺杆和筒壁采用4层边界层网格,流道径向划分为40层网格,流道圆弧等距划分为300份,流域中心3个啮合区的相交部分划分为75份,划分后流道的网格单元数为54000个。网格划分方法如图1(b)、(c)所示。3根螺杆均为同向逆时针旋转,螺杆转速为0.5 r·min-1。

图1 几何模型与流道有限元模型
为了便于求解,采用如下假设:①流动为层流且忽略惯性力的影响;②流动为等温、不可压缩流动;③边界无滑移;④聚合物流体为非牛顿熔体,其黏度与剪切速率的关系可由Bird-Carreau模型表征。
计算中速度、位移采用quadratic插值,压力采用线性插值,黏度采用相对稳定的Picard迭代法。瞬态流场计算采用Crank-Nicolson法,收敛精度为1×10-4。根据三螺杆挤出机二维流场的计算结果,采用Matlab软件编程得到三螺杆挤出机不同时刻的FTLE分布,对计算结果进行可视化研究。
为了验证求解精度,选取3种时间步长:一个时间周期离散为61个时间步长、121个时间步长和241个时间步长。选取3个监测点:中心区P1(0,-1.28)、螺杆壁面P2(0,5.98)、筒壁边缘P3(0, 36.99)。分别采用上述3种时间步长计算初始时刻位于3个监测点的流体粒子的运动轨迹坐标随时间变化曲线,如图2所示。由图2(a)、(b)可知,当粒子位于流道中心P1和螺杆壁面P2时,3种时间步长的计算精度在两个周期内具有较好的一致性。而当粒子位于筒壁边缘P3时,从图2(c)中可以看到,当>160 s时,一个时间周期离散为61个时间步长的计算结果与121个时间步长和241个时间步长的模拟结果出现了相对较大的偏差,但每个周期121个时间步长和241个时间步长的计算结果仍具有较好的一致性,故本工作选用一个时间周期离散为121个时间步长。

图2 时间步长对位置分布的影响
3 模型验证
3.1 网格无关性验证
为验证计算结果的可靠性,首先进行网格无关性验证。将三螺杆挤出机二维几何模型采用四方形结构网格进行网格划分,采用3种网格划分方法:模型1,流道划分为40层,包含54000个单元;模型2,流道划分为40层,包含108000个单元;模型3,流道划分为75层,包含202500个单元。利用Polyflow软件分求解上述3种模型的周期性速度场。图3(b)所示为0 s时3种模型在检测线上[图3(a)]方向的速度分布,可以看到,3种模型在检测线方向的速度分布曲线几乎重合,这说明本工作选用的40层网格包含54000个单元网格的划分方法可以保证模拟的准确性。

图3 网格密度对速度分布的影响
3.2 网格密度对FTLE的影响
基于拉格朗日体系的FTLE准确性与网格密度密切相关。分别采用上述3种网格划分模型计算三螺杆挤出机的FTLE进行比较,如图4所示。从图中可以看到3种网格划分模型计算的三螺杆挤出机FTLE的“脊”结构(LCS)基本相同,为了节省计算时间,选取40层网格包含54000单元,可以确保三螺杆挤出机的FTLE的计算精度。

图4 网格密度对FTLE的影响
4 计算结果与分析
4.1 积分时间对LCS的影响
初始时刻0和积分时间是两个直接影响三螺杆挤出机的FTLE分布的重要参数。其中,积分时间是影响FTLE场中“脊”结构(LCS)完整性的核心要素,选取优质的积分时间可使“脊”完整地出现在FTLE中。由式(5)可知,当时,会导致,即较长的积分时间使FTLE各点的数值相差较小,引起“脊”结构显示不清晰,不易捕捉到LCS。因此,本工作首先分析了积分时间对三螺杆挤出机的LCS的影响。
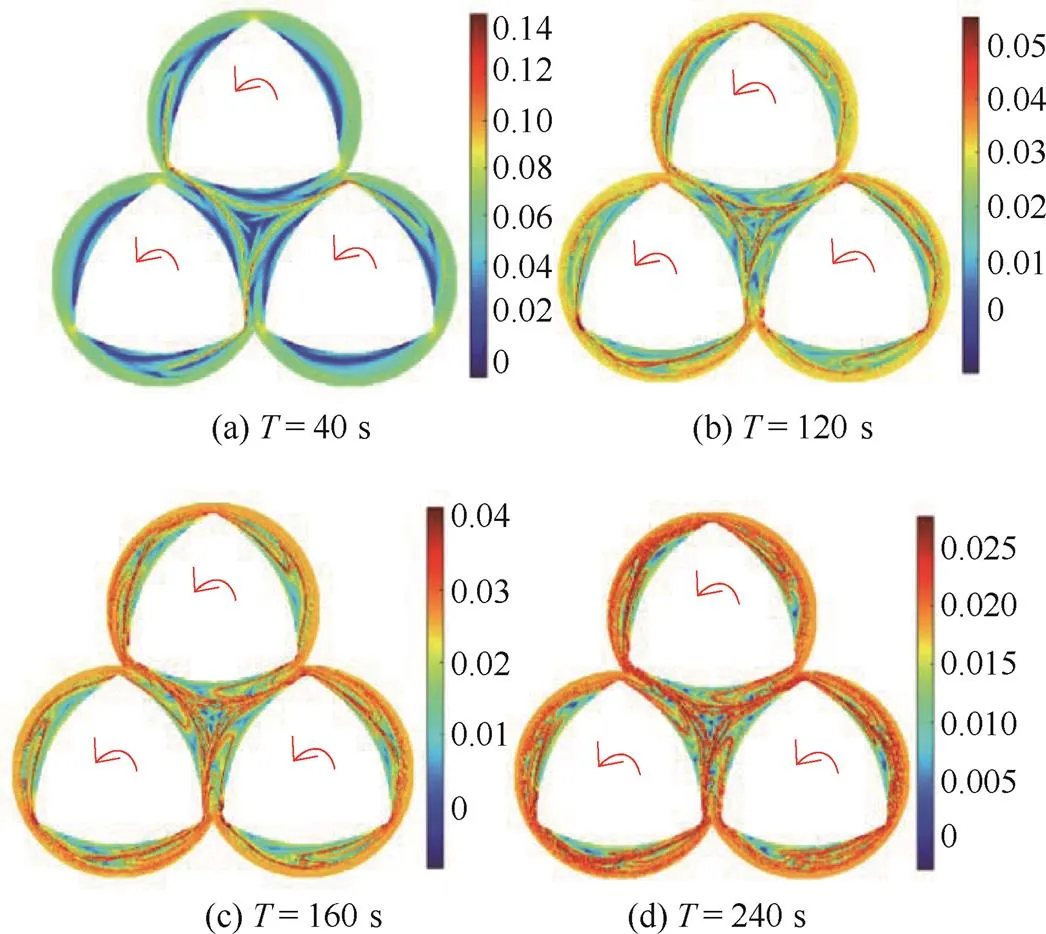
图5 t00 s时不同积分时间三螺杆挤出机的FTLE
图6所示为三螺杆挤出机时间向前的FTLE中提取的LCS分布。由图可见,当积分时间<120 s时,随着的增加,LCS趋于完整;当>120 s时,随着的增加,难以分辨出三螺杆挤出机的LCS的主次。当120 s时,LCS的几何特征已完全显现出来,而且容易捕捉。因此,选用120 s作为三螺杆挤出机内动力系统的FTLE计算的最佳积分时间。
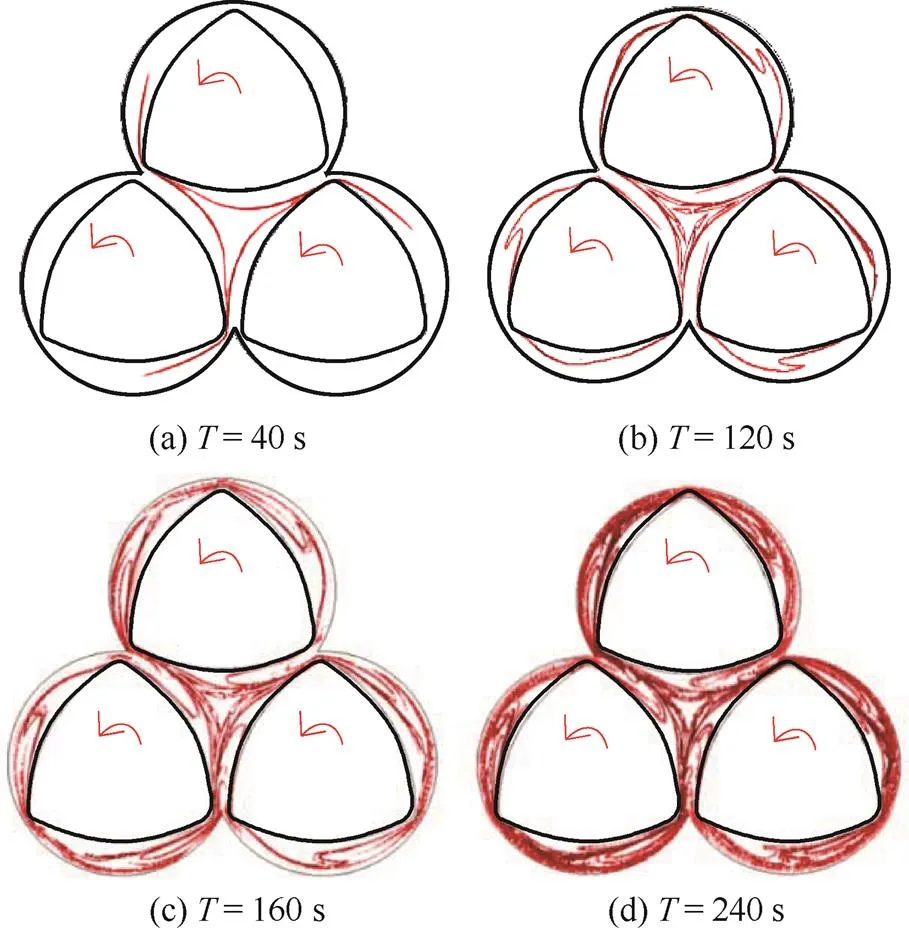
图6 不同积分时间的三螺杆挤出机的LCS分布(t00 s)
4.2 螺杆相位角对LCS的影响
LCS作为物质线的近似,其结构会随螺杆的相位不同发生变化。为了详细分析三螺杆挤出机不同时刻相角下的LCS分布,给出了积分时间120 s时,不同初始时刻、时间向前的三螺杆挤出机的LCS分布,如图7所示。三螺杆挤出机排斥的LCS随螺杆相位角的不同呈现出不同的形状,但无论LCS如何变化,其主要部分总是将三螺杆流域区划分为3个具有不同混合特性的区域,具体将在4.4节中详细分析。此外,从图7中还可以看到LCS中存在多处类似“扭结”的结构。图7(a)中,螺槽中心附近出现了“扭结”,经过1/4周期的转动,“扭结”被逐渐拉伸,同时在图7(d)中螺槽另一侧的中心附近出现了新的“扭结”,这说明螺杆的周期性运动引起物质线产生周期性变化,并随时间循环往复。

图7 不同相位角的排斥的LCS分布(T120 s)
此外,在三螺杆挤出机的中心区也产生了较为复杂的“扭结”,如图8所示。转子的转动带动中心区“扭结”不断重复“产生-拉伸-捏合”的周期性过程。“扭结”引起的流体粒子折叠加强了周围流体的混合。根据动力学理论可知,混沌混合状态下流体粒子的拉伸程度会随时间呈指数增长,而周期性混合状态下流体粒子的拉伸程度仅随时间呈线性增长。拉伸和折叠是产生高效混合的关键,也是混沌产生的必要条件[20],可见三螺杆挤出机内流体的混合具有明显的混沌混合特征。

图8 三螺杆中心区排斥的LCS分布
4.3 混合动力学分析
为了便于在有限时间动力系统中分析三螺杆流场的全局混合特性,将三螺杆挤出机积分时间±120 s时排斥(红色)和吸引(绿色)的LCS绘制于同一流场中,如图9所示。螺杆的转动引起流道几何形状改变,导致LCS也随之变化,特别在流域的中心区,随着中心区面积的逐渐减小,LCS所围成的封闭区域的面积也逐渐减小。图9中,稳定流型与非稳定流型相交出现多个交点,中心区附近的交点中包含了双曲固定点,表明三螺杆挤出机流体混合存在混沌混合特性。

图9 三螺杆流场排斥的LCS和吸引的LCS
流体粒子经过双曲固定点,沿稳定流型的法线方向受到强拉伸作用,使得稳定流型两侧的粒子以指数速率发生分离,有利于流体在三螺杆挤出机的混合腔内充分混合。为清晰地显示中心区相交的LCS结构,图10给出了中心区LCS局部放大图。

图10 中心区排斥的LCS和吸引的LCS
结合图10中LCS的相交结构与中心区的流线分布可以判断,在三螺杆挤出机混合腔的中心区附近存在3个双曲固定点。中心区面积改变,固定点的位置随之改变。
周期点是混沌混合的标志。双曲固定点和椭圆周期点作为周期点的两种表现形式,双曲固定点与流型的性质有关,椭圆周期点则出现在非混沌混合区[21-22],因此椭圆周期点出现的位置混合效果相对较差。由多周期回归点的集合构成的Poincaré截面可直观地表现封闭轨线和固定点的周期特性。
通过排斥的LCS和吸引的LCS的相交图可大致推断椭圆周期点所在。取初始时刻位于流场中心区(避开周期点可能出现的区域)的粒子团,跟踪粒子团中400个粒子在550个周期内的运动轨迹,记录每个()时刻粒子的位置坐标,合并这些粒子点的位置绘制如图11(a)所示的Poincaré截面。从图11(a)中可以看出在三螺杆中心区的中心区出现了KAM“岛”。将中心区的Poincaré截面放大,如图11(b)所示,出现了椭圆周期点结构。椭圆周期点是非混沌区的标志,因此三螺杆中心区存在非混沌混合区域,该区内混合效果相对较差。需要说明的是,由于粒子的随机运动,三螺杆挤出机的大部分混沌结构被众多粒子的运动掩盖,对于混沌区内部的混合状态仍不易看出。

图11 三螺杆挤出机的Poincaré截面
4.4 三螺杆挤出机粒子可视化结果
根据LCS具有的流型性质,初始时刻位于其两侧的粒子经过双曲固定点会沿非稳定流型方向以指数速率相互分离,沿着吸引的LCS输送,因此LCS成为系统中无形的边界。作为输送的准边界,在运动过程中穿过这个边界的物质非常少,在一定程度上可以忽略[13]。根据LCS的准边界特性,三螺杆挤出机流道可分为3个具有不同混合特性的区域,如图12所示,黄色部分区域为LCS包围的远螺杆区,橙色部分区域为LCS包围的近螺杆区,蓝色部分区域为封闭的LCS包围的中心区。

图12 三螺杆挤出机流域分区
为进一步理解三螺杆挤出机的局部混合特性,在3个分割区内分别释放粒子进行可视化分析,计算结果如图13所示。
图13(a)为远螺杆区筒壁相交处流体粒子轨迹的可视化结果,图中位于筒壁尖端的3个粒子团在经过2个周期运动后基本没有离开远螺杆区,这些粒子团在该区域中仅仅被拉伸,没有出现折叠现象,此时的混合为常规的层流混合。因此,远螺杆区混合效果相对较差。
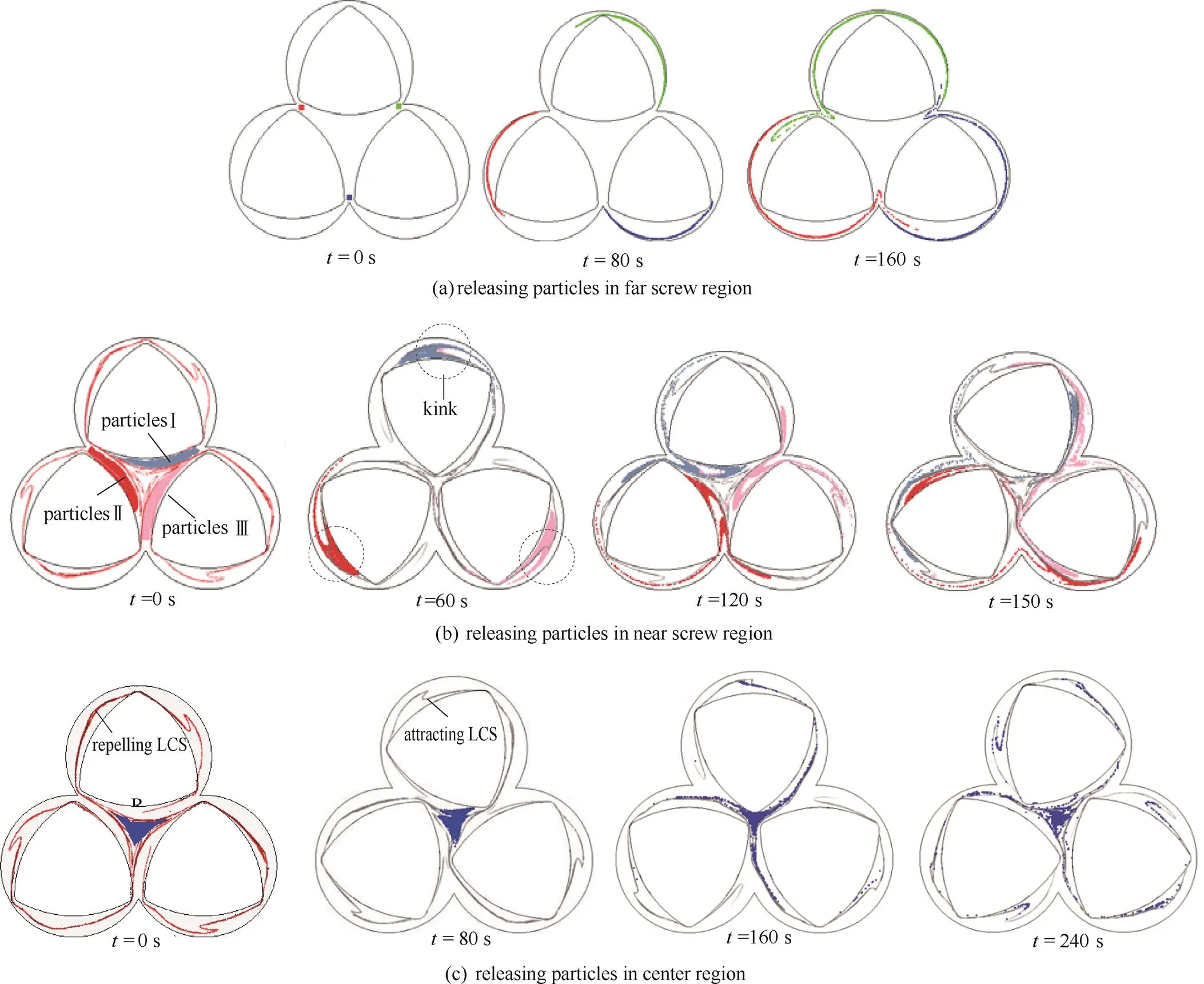
图13 不同LCS分割区释放粒子可视化结果
其次讨论近螺杆区。在中心区附近的近螺杆区被LCS分成3个区域,在3个子区中分别释放红色、粉色和蓝色的粒子团,如图13(b)所示。从图中可以看到,随着螺杆的转动,3个粒子团沿吸引的LCS分别进入3根螺杆流道。当60 s时,在“扭结”的作用下,一部分处于近螺杆区的流体粒子进入到远螺杆区,并在远螺杆区内随准周期轨道运动。因此,“扭结”结构成为远、近螺杆区流体粒子交换的媒介,增强了流体混合的均匀性。由于扭结结构循环产生(图7),其在混沌混合中具有重要的强化作用。当120 s时,粒子团经过一个周期后重新回到初始位置,经过啮合区附近,在非稳定流形的作用下粒子团产生背离LCS的运动,并随螺杆转动而逐渐被拉长,而且在螺杆啮合区发生折叠。说明在流域中心,螺杆啮合区附近有双曲固定点的存在。发生背离的粒子团随螺杆转动进入不同的螺杆流道内。在=150 s时,部分回到中心区的流体粒子再次经过双曲固定点,再次被拉伸,并在流道内重新排列,使混合效率进一步增强。可见双曲固定点的存在极大地提高了三螺杆挤出机的混合效率,使得近螺杆区具有相对较高的混合效率。
最后讨论三螺杆挤出机的特殊区域——中心区。中心区是由封闭的LCS结构包围的区域。在封闭中心区释放粒子,可视化结果如图13(c) 所示。随着螺杆的转动,中心区面积呈现大-小-大的变化规律,LCS封闭的中心区面积也随之变化。当80 s时,一部分流体粒子开始从封闭的中心区分离出来。当160 s时,中心区面积和LCS封闭面积均为最小,从封闭的中心区分离出来的大量流体粒子在非稳定流形的作用下沿着吸引的LCS流出中心区,另一部分粒子受LCS的边界特性影响仍被封闭在中心区内,仅在中心区内进行混合。结合图11中Poincaré截面中心区粒子回归点的运动规律以及图5中FTLE显示的中心区蓝色较小值,可知LCS封闭的中心区混合能力相对较弱。
4.5 单螺杆、双螺杆和三螺杆混合机理对比
将拉格朗日分析方法应用于单螺杆挤出机与双螺杆挤出机内流体的混合机理分析。如图14所示,随着积分时间的增加,单螺杆挤出机流道内的LCS除螺旋程度增加外,没有固定点和“扭结”结构产生。FTLE场图中螺杆周围的蓝色区域混合较差,即为混合的“死区”。流道内的流体仅依靠层流流动实现混合[20,23],混合效率相对较低。

图14 单螺杆挤出机不同积分时间的FTLE场
在螺杆周围(除去死区部分)释放粒子团,其可视化结果如图15所示。由图可见,240 s内流体粒子均没有离开释放区,而且未与释放区以外的流体发生混合。在释放区内部,两种颜色粒子团之间混合呈现螺旋形分层结构,与LCS的形状一致,因此可说明单螺杆挤出机内的流体沿着LCS准边界进行流体输运。
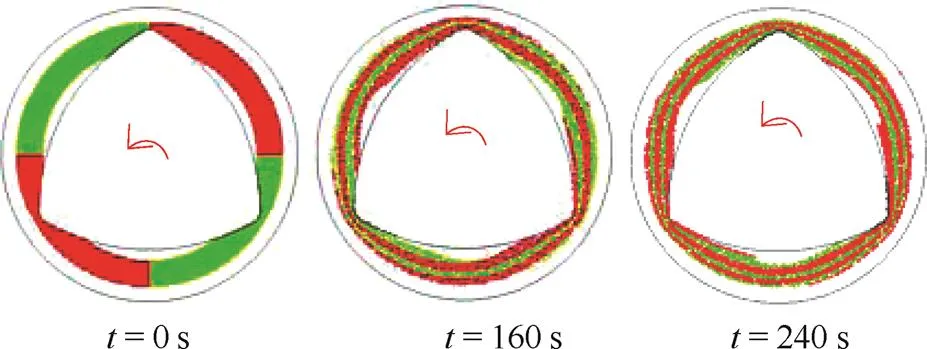
图15 单螺杆挤出机粒子可视化结果
合并双螺杆挤出机流道内排斥的LCS(红色)和吸引的LCS(蓝色),如图16所示。双螺杆挤出机流道被LCS分为近螺杆区(Ⅰ,Ⅱ)和远螺杆区两个部分,并且两种LCS在流道中心出现一处双曲固定点,流道的两侧出现了“扭结”。因此双螺杆挤出机内同样存在混沌混合。
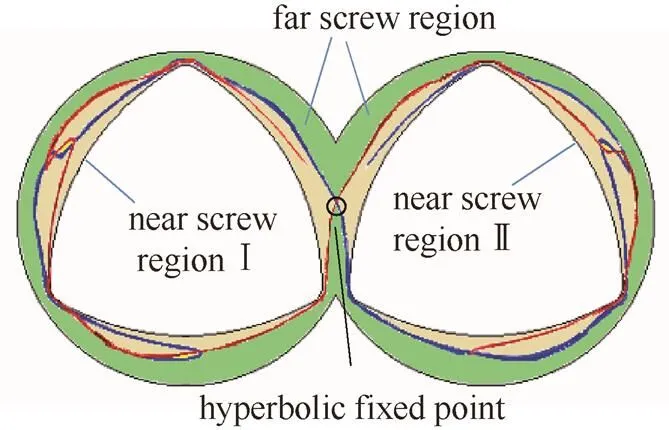
图16 双螺杆挤出机内(T±120 s)排斥的LCS和吸引的LCS
在排斥的LCS两侧,远螺杆区和近螺杆区Ⅱ中分别放置一个粒子团,追踪两个粒子团的运动轨迹,比较两个区域中流体的不同混合特性,其可视化结果如图17所示。图中近螺杆区中的红色粒子团在150 s时经过双曲固定点,沿非稳定流形(图16中蓝色LCS)发生分离,分别进入左、右两侧的近螺杆区(Ⅰ,Ⅱ),受到了较好的拉伸作用,说明该区中的粒子发生了较好的混合。远螺杆区中的蓝色粒子团,由于物质线的封闭导致流体的输运受阻,经过150 s后依然附于筒腔内壁,未与红色的粒子发生混合,即该区中的混合仅为常规的层流混合,混合效果相对较差。总体上,两个粒子团始终在各自区域内运动而没有发生混合。通过以上两个粒子团运动轨迹的追踪可以说明,即使初始时刻两个粒子团距离较近,如果位于两个不同的LCS分割区,其混合效果也会具有明显的差异。

图17 双螺杆挤出机粒子可视化结果
图18为单螺杆、双螺杆和三螺杆挤出机流道内整体对数拉伸曲线的比较(单螺杆挤出机和双螺杆挤出机端面尺寸、几何结构以及网格密度等参数均与三螺杆挤出机各项参数一致)。图中,三螺杆挤出机的对数拉伸最大,其次是双螺杆挤出机,单螺杆挤出机的对数拉伸最小。这是因为三螺杆挤出机的双曲固定点数量最大。当流体经过双曲固定点时,在流型作用下,流体沿非稳定流型的法线方向受到强拉伸作用,因此三螺杆挤出机的平均对数拉伸最大。而单螺杆挤出机无双曲固定点存在,因此其对数拉伸相对较小。
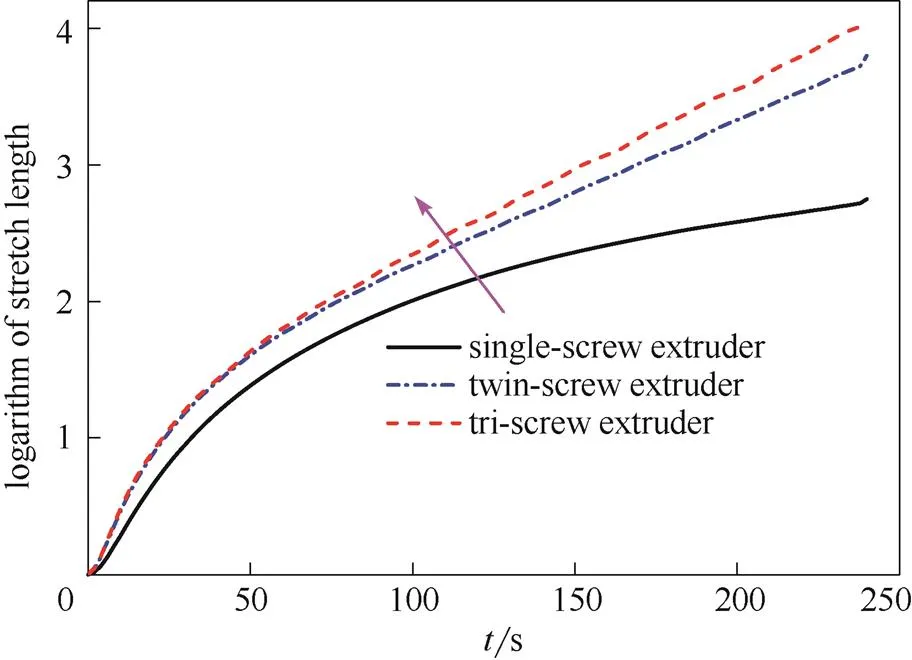
图18 三种螺杆挤出机对数拉伸比较
5 结 论
采用FTLE和LCS并结合Poincaré截面和粒子可视化技术对三螺杆挤出机流体的混沌混合特性进行了分析,讨论了中心区动态结构特性对FTLE和LCS分布的影响,并与单螺杆挤出机和双螺杆挤出机进行了对比分析,得到以下结论。
(1)LCS将三螺杆挤出机流域划分为3个具有不同运动特性的区域:近螺杆区、远螺杆区和中心区。其中,中心区封闭的LCS导致中心流体粒子的输送受到阻碍;在LCS的近螺杆区,由于流域中心双曲固定点的存在,该区域的流体粒子出现明显的拉伸和折叠现象,并在流形作用下重组,产生了高效的混沌混合;在LCS的远螺杆区,在流形的阻碍作用下该区中的粒子仅在区域内发生拉伸和较小的折叠,混合效果相对较弱。因此,远螺杆区是三螺杆挤出机优化设计重点考虑的流动区域。
(2)在三螺杆挤出机中心区附近存在3个双曲固定点,随着中心区形状的变化,双曲固定点的位置随之改变。Poincaré截面的中心区粒子群沿着准周期轨迹运动,出现了椭圆周期点,粒子的流动受到了阻碍。因此,中心区局部混合能力相对较弱。
(3)三螺杆挤出机中LCS循环产生的扭结是近螺杆区、远螺杆区和中心区进行物质交换的桥梁。随着混合时间的增加,扭结的弯曲和折叠程度逐渐增大,增强了近螺杆区、远螺杆区和中心区的物质交换,强化了流场的混沌混合。因此,使三螺杆挤出机流场产生更多的扭结是进行螺杆优化设计的重要依据。此外,中心区LCS封闭结构“小→大→小”的周期性变化也是增强中心区和近螺杆区的物质交换的主要方式。
(4)单螺杆挤出机的LCS呈现出无扭结的螺旋形结构,不存在混沌混合。双螺杆挤出机的LCS在啮合区附近出现1个双曲固定点,并将其流域划分为近螺杆区和远螺杆区两部分。但由于双曲固定点的个数和扭结的折叠程度均不及三螺杆挤出机,双螺杆挤出机混沌混合能力相比三螺杆挤出机较弱。
References
[1] CONNELLY R K, Kokini J L. Examination of the mixing ability of single and twin screw mixers using 2D finite element method simulation with particle tracking [J]. J. Food Eng., 2007, 79 (3): 956-969.
[2] ZHANG X M, Feng L F, Chen W X,. Numerical simulation and experimental validation of mixing performance of kneading discs in a twin screw extruder [J]. Polym. Eng. Sci., 2009, 49 (9): 1772-1783.
[3] DOMINGUES N, Cunha A G, Covas J A. A quantitative approach to assess the mixing ability of single-screw extruders for polymer extrusion [J]. J. Polym. Eng., 2012, 32 (2): 81-94.
[4] NAKAYAMA Y. Melt-mixing by novel pitched-tip kneading disks in a co-rotating twin-screw extruder [J]. Chem. Eng. Sci., 2011, 66 (1): 103-110.
[5] 胡冬冬, 陈晋南.啮合同向三螺杆挤出机中三维等温流动的数值模拟 [J]. 化工学报, 2004, 55 (2): 280-283 HU D D, CHEN J N. Simulation of 3D isothermal flow in intermeshing co-rotating tri-screw extruders [J]. Journal of Chemical Industry and Engineering (China), 2004, 55 (2): 280-283.
[6] JIANG N, ZHU C W. Study on extrusion characteristics of the tri-screw extruder [J]. Polymer-Plastics Technology and Engineering, 2008, 47 (6): 590-594.
[7] ZHU X Z, XIE Y J, MIAO Y. Numerical study on temperature and power consumption of intermeshing co-rotation triangle arrayed tri-screw extruders [J]. Polymer-Plastics Technology and Engineering, 2009, 48 (4): 367-373.
[8] WANG G, ZHU X Z, HE Y D,. Effects of screw clearance and blend ratio on the flow and mixing characteristics of tri-screw extruders in the cross section with CFD [J]. Engineering Applications of Computational Fluid Mechanics, 2013, 7 (1): 74-89.
[9] LEE T H, KWON T H. A new representative measure of chaotic mixing in a chaos single-screw extruder [J]. Advances in Polymer Technology, 1999, 18 (1): 53-68.
[10] HWANG W R, KANG K W, KWON T H. Dynamical systems in pin mixers of single-screw extruders [J]. AIChE Journal, 2004, 50 (7): 1372-1385.
[11] 徐百平, 喻慧文, 何亮,等. 利用往复扰动螺棱强化单螺杆挤出机内混合模拟表征 [J]. 化工学报,2012, 63 (7): 2077-2084. XU B P, YU H W, HE L,. Simulation of enhancement of mixing in single screw extruder by reciprocating barrier [J]. CIESC Journal,2012, 63 (7): 2077-2084.
[12] 程志飞, 何延东, 朱向哲, 等. Roller转子密炼机聚合物流体的混沌混合特性 [J]. 高分子材料科学与工程, 2013, 43 (12): 128-132. CHENG Z F, HE Y D, ZHU X Z,. Chaotic mixing of polymer melt in internal mixer with Roller rotors [J]. Polymer Materials Science and Engineering,2013, 43 (12): 128-132.
[13] GREEN M A, ROWLEY C W, HALLER G. Detection of Lagrangian coherent structures in three-dimensional turbulence [J]. Journal of Fluid Mechanics, 2007, 572 (1): 111-120.
[14] PEACOCK T, DABIRI J. Introduction to focus issue: Lagrangian coherent structure [J]. Chaos, 2010, 20 (1): 1-10.
[15] BOZORGMAGHAM A E, ROSS S D. Atmospheric Lagrangian coherent structures considering unresolved turbulence and forecast uncertainty [J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22 (1/2/3): 964-979.
[16] HALLER G, YUAN G. Lagrangian coherent structures and mixing in two-dimensional turbulence [J]. Chaos, 2000, 10 (1):99-108.
[17] SHADDEN S C, LEKIEN F, MARSDEN J E. Definition and properties of Lagrangian coherent structures from-finite Lyapunov exponents in two-dimensional aperiodic [J]. Physica D: Nonlinear Phenomena, 2005, 212 (3/4): 271-304.
[18] SANTITISSADEEKORN N, BOHLD, BOLLT E M. Analysis and modeling of an experimental device by finite-time Lyapunov exponent method [J]. International Journal of Bifurcation and Chaos, 2009, 19 (3): 993-1006.
[19] ROBINSON M J, CLEARY P W. The influence of cam geometry and operating conditions on chaotic mixing of viscous fluids in a twin cam mixer [J]. AIChE Journal, 2011, 57 (3): 581-598.
[20] OTTINO J M. The Kinematics of Mixing: Stretching, Chaos and Transport [M]. Cambridge: Cambridge University Press, 1989.
[21] Farazmand M, Haller G. Attracting and repelling Lagrangian coherent structures from a single computation [J]. Chaos, 2013, 23: 023101.
[22] ANDERSON P D, GALAKTIONOV O S. Mixing of non-Newtonian fluids in time-periodic cavity flows [J]. Non-Newtonian Fluid Mech., 2000, 93: 265-286.
[23] Aref H. Stirring by chaotic advection [J]. Journal of Fluid Mechanics, 1984, 143: 1-21.
Analysis of 2D flow chaotic mixing at cross section of tri-screw extruder by Lagrangian coherent structure
TONG Ying, ZHU Xiangzhe, GAO He, HE Yandong
(School of Mechanical Engineering, Liaoning Shihua University, Fushun 113001, Liaoning, China)
As a novel equipment for polymer fluid processing, the tri-screw extruder has very complex mixing mechanism due to periodic change in geometrical structures and stresses at its unique center region. Chaotic mixing in tri-screw extruder was analyzed by Lagrangian system, which is much different from the traditional linear mixing analysis technique. With the finite-time Lyapunov exponent (FTLE), Lagrangian coherent structure (LCS), Poincaré section and particle visualization technology, mechanism of fluid transfer and chaotic mixing in 2D flow field as well as influence of dynamic structure characteristics at the center region to the FTLE’s and LCS’s distributions were studied in tri-screw extruder and compared to those in single- and twin-screw extruders. The results show that LCS divided the flow field in tri-screw extruder into three regions of different flow characteristics, namely, the near screw region, the far screw region and the center region, where a snarl is mass transfer bridge connecting these three regions. With the increase of mixing time, the degree of bending and folding in the snarls increased gradually, that enhanced chaotic mixing in flow field of tri-screw extruder by increasing transportation of polymer melt across three regions. Three hyperbolic fixing points near the kneading block indicated good mixing capability. The existence of elliptical cycle points in the Poincaré cross-sections implied the presence of non-chaotic spots in the center of flow field. Thus, mixing in the center region of tri-screw extruder was relatively poor.
tri-screw extruder; finite-time Lyapunov exponent; Lagrangian coherent structure; chaotic mixing; flow; CFD; numerical analysis
2016-02-17.
Prof. ZHU Xiangzhe, xzzhu@126.com
10.11949/j.issn.0438-1157.20160178
TQ 320.5
A
0438—1157(2016)10—4378—11
国家自然科学基金项目(51473073,51303075);辽宁省自然科学基金项目(2015020142)。
2016-02-17收到初稿,2016-07-05收到修改稿。
联系人:朱向哲。第一作者:佟莹(1991—),女,硕士研究生。
supported by the National Natural Science Foundation of China (51473073, 51303075) and the Natural Science Foundation of Liaoning Province (2015020142).

