基于奇异值分解的岩心高光谱数据降噪研究

杨　浩，柳炳利，张二喜，郭　科

（成都理工大学 数学地质四川省重点实验室，四川 成都　610059）

基于奇异值分解的岩心高光谱数据降噪研究

杨浩，柳炳利，张二喜，郭科

（成都理工大学 数学地质四川省重点实验室，四川 成都610059）

为了更有效地消除岩心高光谱数据中的噪声，提出基于奇异值分解的岩心高光谱数据降噪方法，引入奇异值下降率的概念，利用奇异值下降率单调性的突变点来确定表征信号有用奇异值的个数。用该方法对地物光谱仪ASD Field⁃Spec®4实地采集到的岩心高光谱数据进行降噪处理，并与依据奇异值相对强度确定奇异值突变点的降噪方法进行对比，利用均方根误差（RMSE）、信噪比（SNR）两项指标对降噪效果进行评价。实验结果表明，该方法更能提高信噪比，降低均方根误差，更能有效保持原始岩心高光谱曲线的吸收特征，消除高光谱曲线上的毛噪现象。

奇异值分解；奇异值下降率；岩心高光谱数据；降噪

0　引　言

高光谱数据蕴含了丰富的岩石、矿物的反射光谱信息，但在实际野外采集光谱的过程中，周围环境因素和一系列的人为因素都会使采集到的光谱数据含有大量噪声，例如：光照条件的变化，周围环境湿度、温度等自然条件。这严重影响了地物反射光谱中的吸收特征，大大降低了数据的分析精度。因此，对高光谱数据的降噪研究是极其必要的。

国内外不少学者对高光谱数据降噪进行了研究。Boardman和Kruse提出了用最小噪声分离技术（MNF）隔离高光谱数据中的噪声［1］；徐冬等提出了一种基于多元线性回归的高光谱遥感数据去噪方法［2］；印佳等使用主成分分析进行高光谱数据去噪［3］；陈志刚等提出了基于经验模态分解高光谱图像光谱域去噪方法［4］；周丹等应用小波阈值对高光谱进行小波分析去除光谱噪声［5］；路威等实现了高光谱遥感数据的三次光滑样条去噪［6］。

以上方法大都基于光谱曲线的平滑处理，容易造成光谱特征丢失，而小波分析处理高光谱噪声一般需要估计噪声的统计特征来确定小波阈值，对噪声水平有一定依赖性。为了寻求能够适应高光谱降噪要求的降噪方法，本文利用Hankel矩阵和SVD（奇异值分解）对野外实地采集到的岩心高光谱数据进行降噪研究，引入了奇异值下降率的概念，以确定奇异值个数。

1　Hankel矩阵和SVD

Hankel矩阵是指每一条副对角线上的元素都相等的方阵。设方阵 A=［ai，j］m×n∈Cm×n，如果 ai，j=ai-1，j+1i-1，则称矩阵 A为Hankel矩阵。SVD（Singular Value De⁃composition）即矩阵的奇异值分解，是现代数值分析最基本和最重要的工具之一。SVD在最优化问题、统计学、信号处理以及工程技术等方面都有重要作用。

设 A∈Cm×n，且r=rank（A），因为 AHA是半正定矩阵，且rank（AHA）=rank（A）=r，所以AHA的特征值可以排列 为 ：λ1≥λ2≥…≥λr＞0=λr+1=λr+2=…=λn则 称为A的奇异值，λi为 AHA的特征值。进一步，存在m阶酉矩阵U和n阶酉矩阵V，使得：

成立。其中Σ=diag（σ1，σ2，…，σr），而σi（i=1，2，…，r）称为矩阵A的正奇异值，此时式（1）称为矩阵A的奇异值分解式［7］。将式（1）写成求和形式有：

式中：ui为AAH的第i个单位特征向量；vi为AHA的第i个单位特征向量。

2　SVD降噪原理

基于SVD分解的滤波方法是一种非线性滤波，它从矩阵的角度出发，将包含信号特征的矩阵分解到一系列奇异值和奇异值矢量对应的子空间中［8］，本文将实测岩心高光谱数据构造成Hankel矩阵，然后对Hankel矩阵进行奇异值分解，进行降噪处理，最后重构岩心高光谱信号，得到降噪后的岩心高光谱信号。

野外实测岩心高光谱反射率序列x为：

式（4）中：s（i）代表去噪后的岩心高光谱反射率信号；n（i）代表噪声信号，i=1，2，…，N，N为光谱反射率数据序列长度。由H（i，j）=x（i+j-1）构造m×n阶Hankel矩阵［9］：

式中［10］，N=m+n-1。

将式（4）代入式（5）有：

式中：Hs为去噪后的岩心高光谱反射率信号 s（i）的m×n阶Hankel矩阵Hs（i，j）=s（i+j-1）；Hn为噪声n（i）的m×n阶Hankel矩阵 Hn（i，j）=n（i+j-1）；对 H进行奇异值分解，有：

参照式（2），将式（7）写成：

式（7）、式（8）中，酉矩阵U∈Cm×m，酉矩阵V∈Cn×n，且U=［u1，u2，…，um］，V=［v1，v2，…，vn］，σi（i=1，2，…，r）为矩阵H的正奇异值，r=min（m，n），Σ=diag（σ1，σ2，…，σr），ui为 HHT的第i个单位特征向量，vi为 HTH的第i个单位特征向量。选取前L个奇异值及其对应的特征向量重构H的逼近矩阵：

经过SVD分解并依据信号和噪声各自的特点，即真实信号s（i）与噪声信号n（i）之间的不相关性［11］，以及真实信号能量比较集中，而噪声信号能量比较分散的特点，可以将由含噪的测量信号所构成的Hankel矩阵分解成两个互不相关的空间：真实信号空间和噪声空间，从Hankel矩阵H中去除噪声空间，就能够得到经过滤波后的信号空间，进而得到降噪后的信号。一般而言，不再是一个Hankel矩阵，必须构造一个Hankel矩阵如式（9）所示，来逼近，按照式（9）来构造，对矩阵Hs的反对角线求平均值即可得到真实信号在每一时刻的值［9］s（i），i=1，2，…，N。同理，矩阵的反对角线求平均值，从而得到经过降噪后，真实信号在每一时刻的估计，即SVD降噪后的信号。

3　奇异值下降率

SVD降噪的关键在于奇异值个数L的选取。Hanli Qiao提出以下规则［12］确定L：将H的奇异值从大到小排列，依次为σi（i=1，2，…，r），选取前L个奇异值之和与所有奇异值之和之比刚好超过90%的L作为SVD降噪的奇异值个数。张波使用奇异值相对强度曲线［8］的突变点确定降噪奇异值个数L，赵学智提出奇异值差分谱理论［13］，bi=σi-σi+1，i=1，2，…，r-1，以差分谱bi的第二个最大峰值所在坐标i作为降噪奇异值个数L。

第一种确定奇异值个数的方法，参数90%的确定太主观；第二种方法对于奇异值相对强度曲线突变点的界定仅靠人为观察，会造成较大误差；第三种方法当两相邻奇异值差别不大时，方法失效，不能确定奇异值个数。

本文从奇异值突变角度出发，引入奇异值下降率的概念，以便科学地确定SVD降噪奇异值个数。设奇异值从大到小排序后的序列为（σ1，σ2，…，σr），为描述奇异值序列的突变特性，定义：

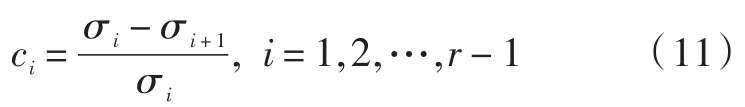
为第i+1个奇异值的奇异值下降率。由于奇异值是按降序排列，它描述了奇异值序列的下降快慢程度，前面的值较大的奇异值描述的是信号的信息。ci大表示第i+1个奇异值较第i个奇异值下降得快，ci小表示第i+1个奇异值较第i个奇异值下降得慢，ci单调递减时奇异值表征了信号，当ci在i点单调性发生变化，即此位置前后奇异值在性质上出现了突变，说明i点以后的奇异值表征了噪声的信息。取前i个奇异值进行SVD降噪处理。

4　岩心高光谱数据SVD降噪处理

本次研究的岩心高光谱数据是利用美国ASD公司生产的地物光谱仪ASD FieldSpec®4在湖北省鸡冠咀铜金矿岩心库实地采集的。ASD FieldSpec®4是为针对地物环境遥感研究而专门设计的，能够有效地获取可见和近红外光谱（Visible and Near⁃Infrared，VNIR），短波红外光谱（Short⁃Wave Infrared，SWIR）。该仪器采集光谱范围：350～2 500 nm。实测含噪岩心高光谱如图1所示。由于ASD地物光谱仪采用了三个探测器：350～1 000 nm是512阵元PDA探测，1 000～1 800 nm 及1 800～2 500 nm两个独立的InGaAs探测器。导致采集到的岩心高光谱数据在波长1 000 nm和1 800 nm处的反射率出现了阶跃变化。需要对实测光谱进行阶跃处理，消除阶跃，消除阶跃后的岩心高光谱曲线如图2所示。

由于Hankel矩的秩r=min（m，n）；r太大会导致Hankel矩阵非零奇异值个数过多，难以用少数几个奇异值表征信号，r太小，会使噪声和信号难以分离；取Han⁃kel矩阵的维数为2 080×72，由图2中的岩心高光谱反射率数据构造Hankel矩阵G，对矩阵G进行奇异值分解。奇异值分布曲线如图3所示；奇异值相对强度曲线如图4所示；奇异值差分谱如图5所示；奇异值下降率曲线如图6所示。

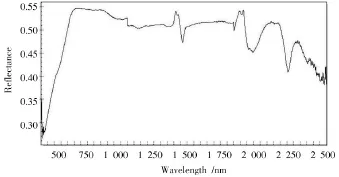
图1　实测含噪岩心高光谱曲线

图2　处理阶跃后含噪岩心高光谱曲线

图3　奇异值分布曲线

图4　奇异值相对强度曲线

图5　奇异值差分谱曲线

图6　奇异值下降率曲线

对于Hnakel矩阵G的奇异值的突变点的界定，图3和图4的方法都指示第2个奇异值为突变点，而图5差分谱并没有出现波峰波谷，方法失效。取前2个奇异值进行SVD降噪，降噪后光谱曲线如图7所示。本文提出奇异值下降率曲线确定奇异值个数，奇异值下降率曲线如图6所示，第9个点以前的奇异值下降率程依次递减关系，在第10个点处的奇异值下降率大于第9个点的奇异值下降率，说明奇异值发生了突变，有噪声掺杂到信号中了，取突变以前的9个奇异值进行SVD降噪处理。降噪后光谱曲线如图8所示。以两种方式确定突变点的SVD降噪方法去噪指标对比如表1所示。

图7　奇异值相对强度确定突变点降噪后光谱曲线

由表1可以看出，与以奇异值相对强度确定奇异值突变点的SVD降噪方法相比，本文提出的以奇异值下降率确定SVD突变点的降噪方法具有高信噪比，低均方根误差的特点。

图8　奇异值下降率确定突变点降噪后光谱曲线

表1　两种方法确定突变点SVD降噪指标对比

对比图2，图7，由奇异值相对强度确定奇异值突变点的SVD降噪后岩心高光谱曲线在波长约1 850 nm左右丢失了吸收峰，图2中降噪前岩心高光谱曲线在波长2 250 nm以后的位置隐约有吸收峰存在，但在图7中，2 250 nm以后的吸收特征被去除了，降噪效果存在很大问题。

对比图2，图8，本文提出的奇异值下降率确定奇异值突变点的SVD降噪后光谱曲线保持了降噪前光谱曲线在1 850 nm波长处的吸收特征，并去除了2 250 nm以后的岩心高光谱曲线毛噪现象，凸显了2 300 nm以后的2个吸收峰位。研究表明［14］绿泥石化矿物主要的吸收峰位置为2 360 nm，碳酸盐化矿物的主要吸收峰为2 342 nm，本文的降噪方法准确揭示了2 300 nm以后的岩心高光谱数据的吸收峰，为后续岩心高光谱矿化蚀变信息的提取奠定了基础。

5　结　论

本文提出了基于奇异值下降率确定奇异值突变点的SVD岩心高光谱数据降噪方法，并应用此方法对岩心高光谱数据进行降噪研究，研究结果表明，奇异值差分谱方法不能确定岩心高光谱数据降噪的SVD奇异值个数；奇异值相对强度确定突变点的岩心高光谱数据SVD降噪光谱曲线较原始高光谱曲线，丢失很多吸收峰；奇异值下降率能自动识别岩心高光谱数据SVD降噪过程中的奇异值突变点，无需经验判断，解决了SVD降噪的关键问题；基于奇异值下降率的SVD岩心高光谱数据降噪方法有效去除了岩心高光谱数据中噪声，消除了岩心高光谱曲线的毛噪现象，准确提取了2 300 nm以后的岩心高光谱数据的吸收峰，为后续岩心高光谱矿化蚀变信息的提取奠定了基础。

注：本文通讯作者为柳炳利。

［1］BOARDMAN J W，KRUSE F A.Automated spectral analysis：a geological example using AVIRIS data［C］//Proceedings of the Tenth Thematic Conference on Geologic Remote Sensing. North Grapevine Mountains，Nevada：［s.n.］，1994：407⁃418.

［2］徐冬，孙蕾，罗建书.基于多元线性回归的高光谱遥感图像小波去噪［J］.遥感信息，2013（6）：78⁃81.

［3］印佳，杜战战.基于主成分分析的高光谱遥感图像非局部去噪［J］.现代电子技术，2015，38（11）：70⁃72.

［4］陈志刚，束炯.高光谱图像光谱域噪声去除的经验模态分解方法［J］.红外与毫米波学报，2008，27（5）：378⁃382.

［5］周丹，王钦军，田庆久，等.小波分析及其在高光谱噪声去除中的应用［J］.光谱学与光谱分析，2009，29（7）：1941⁃1945.

［6］路威，余旭初，刘娟.高光谱遥感数据三次光滑样条滤噪［J］.测绘科学技术学报，2005，22（1）：11⁃13.

［7］吴昌悫，魏洪增.矩阵理论与方法［M］.北京：电子工业出版社，2013：79⁃80.

［8］张波，李健君.基于Hankel矩阵与奇异值分解（SVD）的滤波方法以及在飞机颤振试验数据预处理中的应用［J］.振动与冲击，2009，28（2）：162⁃166.

［9］DOCLO S，DOLOGLOU I，MOONEN M.A novel iterative sig⁃nal enhancement algorithm for noise reduction in speech［R/ OL］.［1999⁃07⁃18］.http：//www.researchgate.net/publication/ 28264.

［10］GOLAFSHAN Reza，SANLITURK Kenan Yuce.SVD and Hankel matrix based de⁃noising approach for ball bearing fault detection and its assessment using artificial faults［J］. Mechanical systems and signal processing，2016（70/71）：36⁃50.

［11］高建，张飞艳，谢伟，等.利用能量变分方法进行高光谱数据去噪处理［J］.武汉大学学报（信息科学版），2012，37（3）：322⁃325.

［12］QIAO Hanli.New SVD based initialization strategy for non⁃negative matrix factorization［J］.Pattern recognition letters，2015，63：71⁃77.

［13］赵学智，叶邦彦，陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用［J］.机械工程学报，2010，46（1）：100⁃108.

［14］张媛，张杰林，赵学胜，等.基于峰值权重的岩心高光谱矿化蚀变信息提取［J］.国土资源遥感，2015（2）：154⁃159.

A new method about core hyperspectral data denoising based on singular value decomposition

YANG Hao，LIU Bingli，ZHANG Erxi，GUO Ke
（Sichuan Province Key Laboratory for Mathematical Geology，Chengdu University of Technology，Chengdu 610059，China）

In order to eliminate the noise in the core hyperspectral data more effectively，a new method about core hyper⁃spectral data denoising based on singular value decomposition is proposed，in which the concept of singular value decline rate is brought.The number of useful singular value of the characterization signal is determined by the abrupt change point of the singu⁃lar value decline rate.This method is used to denoise the core hyperspectral data collected by ASD FieldSpec®4，and compared with the denoising method that relies on the singular value relative strength to determine singular value mutation point.Its denois⁃ing effect was evaluated with the root mean square error（RMSE）and the signal⁃to⁃noise ratio（SNR）.The results show that the method can improve SNR，reduce RMSE，keep the absorption characteristics of original core hyperspectral curve more effective⁃ly，and eliminate the frizz phenomenon of core hyperspectral curve.

singular value decomposition；singular value decrease rate；core hyperspectral data；denoising

TN957.54⁃34；TN911.74

A

1004⁃373X（2016）18⁃0004⁃05

10.16652/j.issn.1004⁃373x.2016.18.002

杨浩（1990—），男，彝族，四川喜德人，硕士研究生。主要从事高光谱数据处理的研究工作。柳炳利（1981—），男，讲师，博士。主要从事数学地质、遥感地质方面的研究工作。

2016⁃01⁃27

国家自然科学基金资助项目（41272363）；中国地质调查局地质调查项目：基于岩心高光谱的原生晕地球化学部找矿预测研究（12120114002001）