简化版Trivium算法的线性逼近研究
马猛,赵亚群
简化版Trivium算法的线性逼近研究
马猛,赵亚群
(信息工程大学数学工程与先进计算国家重点实验室,河南郑州 450001)
针对初始化轮数为288个时钟的简化版Trivium算法(又称2轮Trivium)进行了线性逼近研究,设计了搜索最佳线性近似式算法,并通过对第1轮关于密钥、初始化向量和密钥流比特的表达式做非线性逼近,结合该算法,在同等条件下给出了2轮Trivium 16个偏差为的线性近似式,使通过多线性攻击去识别2轮Trivium的一个具有特定比特的密钥所需要的数据量降为个选择,为Turan方案所需数据量的,且成功率保持不变。
流密码;Trivium算法;多线性密码分析;线性逼近
1 引言
由Canniàre和Preneel[1]于2005年设计的Trivium算法是2004年欧洲序列密码计划最终胜选的标准算法之一,该算法面向硬件实现,具有设计简洁、安全、速度快和灵活性好等特点。因此,Trivium在发布之初就引起了广泛关注,针对Trivium的安全性分析一直是流密码的热点研究方向之一。
目前针对Trivium的主要攻击方法有线性攻击、区分攻击、代数攻击、滑动攻击、立方攻击、错误引入攻击等。Maximov和Biryukov[2]在2007年提出了Trivium的代数攻击方法,攻击的计算复杂度为,其中,常数是求解线性方程组的复杂度。2009年,Dinur和Shamir[3]针对初始化轮数为767个时钟的简化版 Trivium提出了立方攻击,攻击的计算复杂度为。2010年,Stankovski[4]对初始化轮数为1 078个时钟的简化版Trivium 进行了区分攻击,攻击的计算复杂度为。2011年,Hu等[5]通过重复错误注入的方式,提出了一种校验部分原始密钥流和部分错误密钥流的方法,确定错误注入时间及位置,进而说明Trivium在故障攻击下的脆弱性,较Hojsík等的故障攻击方法[6],该模型有更弱的假设条件。2014年,Avijit等[7]提出了一种故障攻击方法,在已知117 bit原始密钥流和236 bit错误密钥流的条件下,攻击的计算复杂度是。Prakash等在文献[8]中给出了一种条件很弱的差分错误攻击模型,具有很好的通用性。
Turan等[9]将Trivium的初始化轮数由1 152个时钟数降低为288个,得到了一个简化的版本(即2轮Trivium),在某种弱密钥条件下,找到了该简化版本的一个偏差为的线性近似式,从而可以对其进行单线性密码分析。在此基础上,贾艳艳等[10]找到另一个偏差为的线性逼近,基于多线性密码分析理论,提出了具体的攻击算法,从而可以对其进行多线性密码分析,同时指出,若能找到个相同偏差的线性近似式,多线性密码分析所需的数据量只有单线性密码分析的,且攻击成功的概率保持不变。孙文龙等[11]给出了在弱密钥和选择攻击的条件下搜索最佳线性近似式的算法,据此算法找到了3个偏差为的线性近似式,但是由于密钥不同,不能进行多线性密码分析。欧智慧等[12]通过改变2轮Trivium第一轮的时钟个数,给出了1个偏差为的线性近似式和8个偏差为的线性近似式,使多线性密码分析所需要的数据量降为文献[9]的,具体的攻击算法可见文献[10]。
本文的目的是寻找偏差更大、个数更多的2轮Trivium线性近似式,从而降低对2轮Trivium进行多线性密码分析所需要的数据量,主要工作体现在如下2点:1)在某种弱密钥条件下,通过搜索最佳线性近似式算法给出了偏差为的线性近似式;2)对2轮Trivium的第1轮关于密钥、初始化向量和密钥流比特的表达式做非线性逼近,找到了2轮Trivium的16个偏差为的线性近似式。
2 基础知识
定义1[13]称是随机变量的偏差,称是函数的偏差。若的偏差为,则称函数以偏差逼近。
引理1[14]堆积引理。设是上个独立随机变量,表示的偏差。表示随机变量的偏差,则。
引理2[15]最佳仿射逼近定理。设是元布尔函数,如果,那么当时,为的最佳仿射逼近,当时,为的最佳仿射逼近。
引理3[12]设为元布尔函数,。如果,则。如果,则,其中,为中具有形式的个数。
3 Trivium算法描述
Trivium算法结构由3个移位寄存器构成,级数分别为93、84和111,设、分别表示算法的密钥和初始化向量。Trivium算法初始化阶段首先将80 bit的密钥和80 bit的初始化向量载入到3个移位寄存器内部状态中,93级布态方式为:,84级布态方式为:,111级布态方式为:,然后运行密钥流生成算法,空跑个时钟,此阶段不输出密钥流比特,只为3个寄存器布态,输出为Trivium的内部状态。Trivium算法密钥流生成阶段的算法和初始化阶段算法相同,只是此时输出密钥流,输入为内部状态和密钥数,算法描述如下。
贾艳艳等[10]指出,将Trivium算法可以看作是函数的集合,其中,是由bit和bit生成第个密钥流比特的函数,如果找到了的一个偏差为的线性近似式,将密码再同步次,则一定可以得到密钥的1 bit信息。文献[9~12]的思想是:对Trivium算法进行多线性密码分析时,可以将其初始化阶段像分组密码一样分成轮,将每一轮的线性近似式有效组合,最终得到Trivium算法一个关于(,)和密钥流比特的线性近似式,其偏差可利用堆积引理求得。2轮Trivium的初始化轮数为288个时钟,文献[9~11]选择对称分轮,将144个时钟作为一轮来分析2轮Trivium;文献[12]选择不对称分轮,分别设定第一轮所占时钟个数为141、154来分析2轮Trivium。
4 研究结果
对于给定的密码算法,线性密码分析的关键是找到它的线性近似式。针对2轮Trivium,一般的做法是首先对每轮进行线性逼近,然后将各个线性逼近有效地组合,得到最终的线性近似式。事实上,也可以通过对第1轮求具有较大偏差的非线性近似式,对第2轮求线性近似式,有效组合得到2轮Trivium的线性近似式,这也是本文的思想。
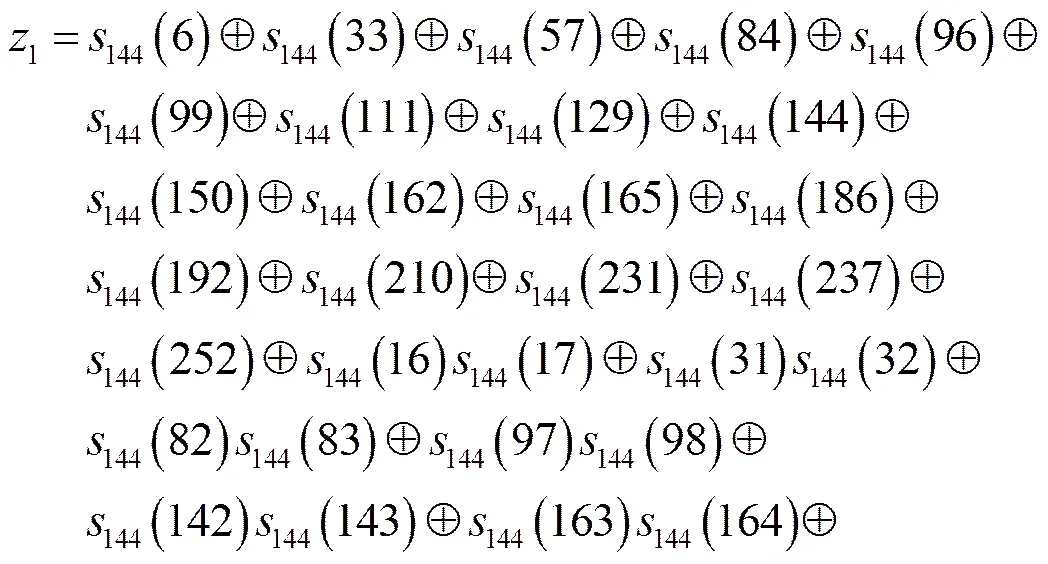
(1)
用非线性二次函数
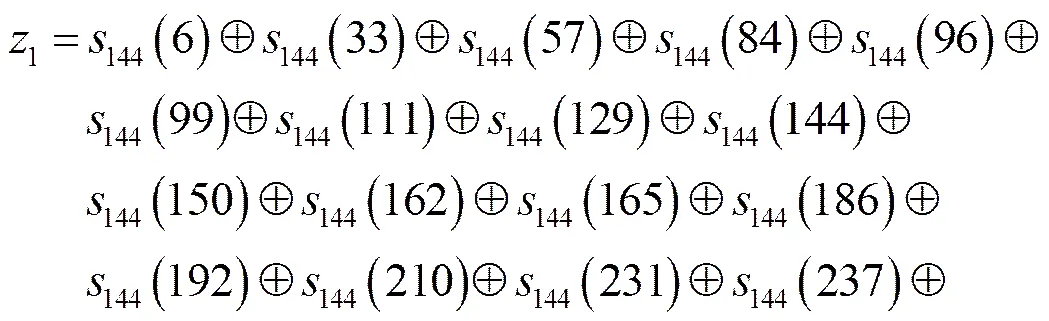
(2)

(3)
综合式(1)~式(3),由堆积引理得到式(3)成立的偏差为,其中,为密钥的规模。但是这个偏差太小,对于实际的线性分析没有意义。此时,可以通过选择特殊密钥和增大式(3)成立的偏差,这对于选择攻击来说并不困难。设表示为零的密钥比特集合,表示为零的比特集合。、分别表示、的规模。、分别表示给定、并化简剩余的二次项、三次项的个数,由堆积引理,此时式(3)成立的偏差为
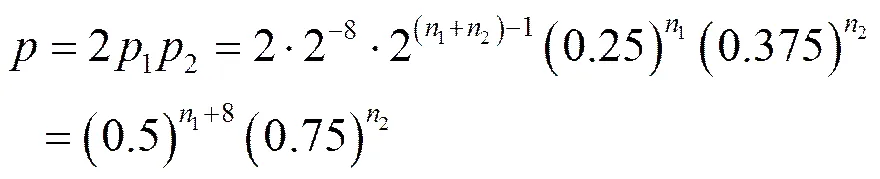
算法1 搜索最佳线性近似算法
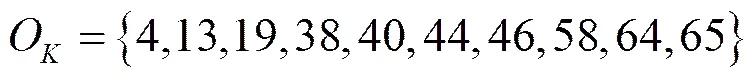
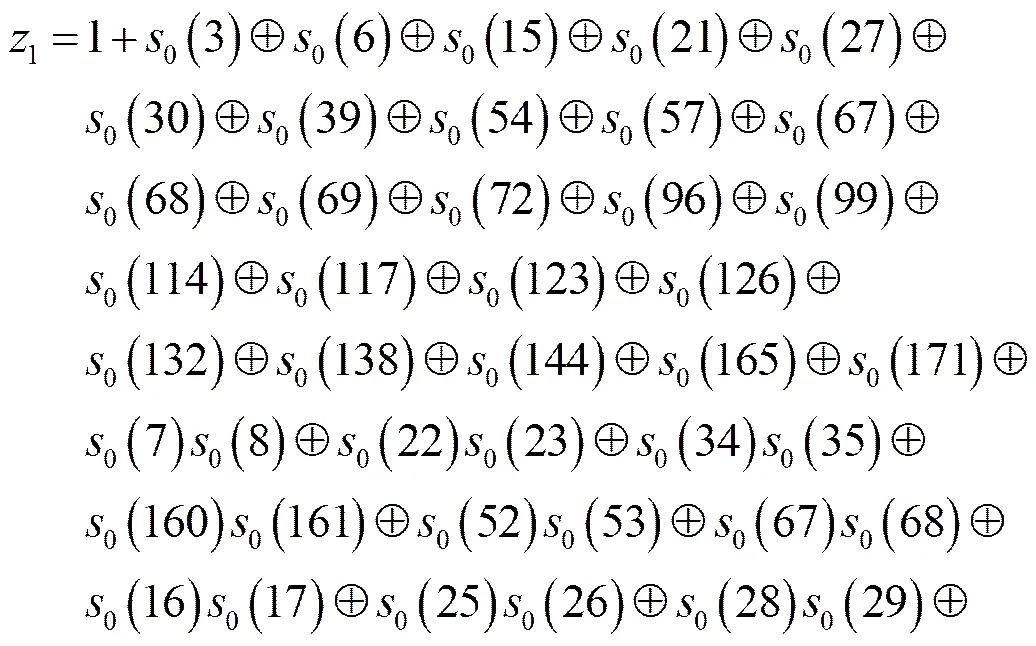
(5)
式(5)中的各个非线性项数量相互独立,有24个线性项,15个二次项,1个三次项,代入式(4),式(3)成立的偏差为:,由上述分析可知式(6)即为偏差最大的2轮Trivium线性近似函数。
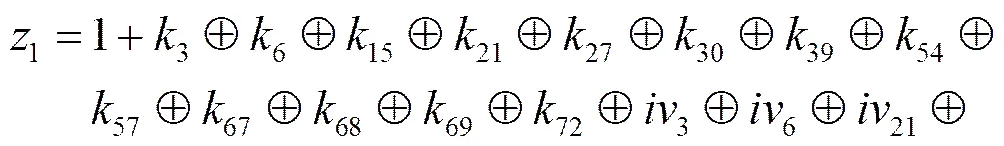
(6)
孙文龙等[11]在指定10 bit密钥和10 bit为零的前提下,通过算法得到了偏差为的最佳线性近似式。而对于同样的目标函数式,执行本文给出的算法1,输入,最佳线性近似式以偏差成立。用类似于式(2)的多个非线性式去逼近式(1),可以得到多个不同的2轮Trivium线性近似式。选择非线性式的原则是:来自式(1)的非线性项,或可以被式(1)的非线性项合并,且使关于的函数表达式具有较低次数和较少非线性项。多线性密码分析要求识别的是具有特定比特的密钥,所以指定密钥为零的比特必须是相同位置上的。另外,选取时,特定比特尽量在相同位置上,这样选择攻击将会易于操作,便于实施。取不同的非线性式逼近式(1),执行算法1,令,输入,仅搜索,得到了16个偏差为的线性近似式,具体的结果如表1所示。基于这16个线性近似式可对2轮Trivium进行多线性密码分析,具体算法可见文献[10]。
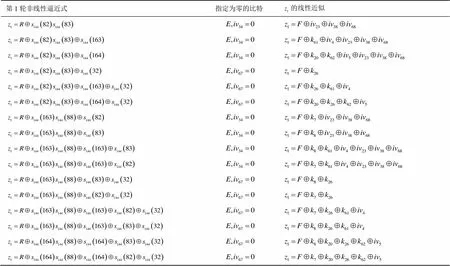
表1 t1=144时z1的16个偏差为2−23.42线性近似
为了方便表示,给出如下记号
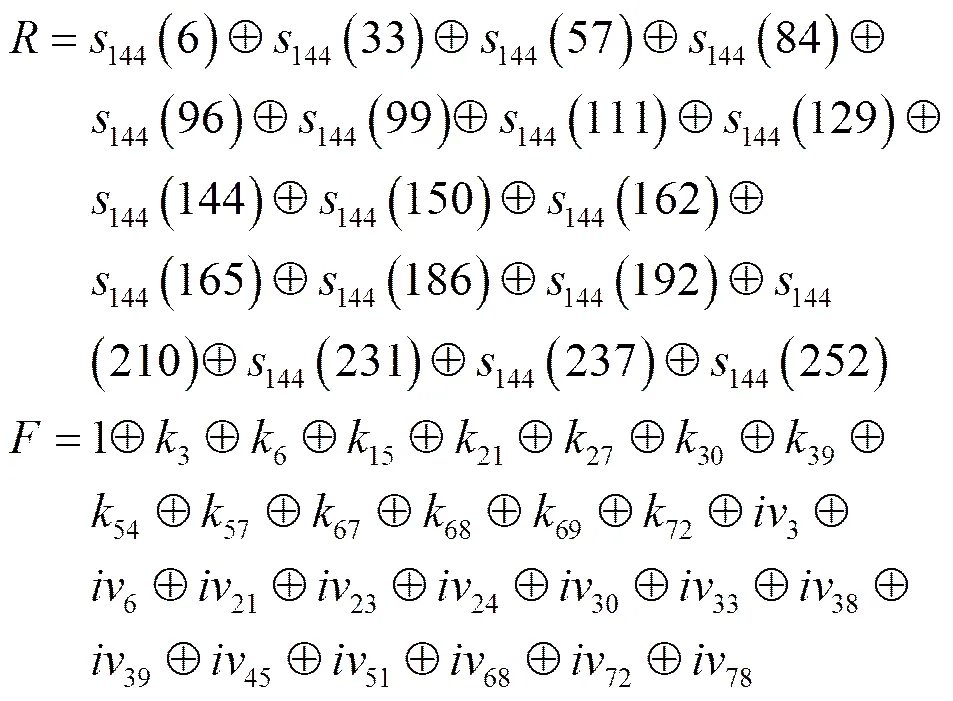
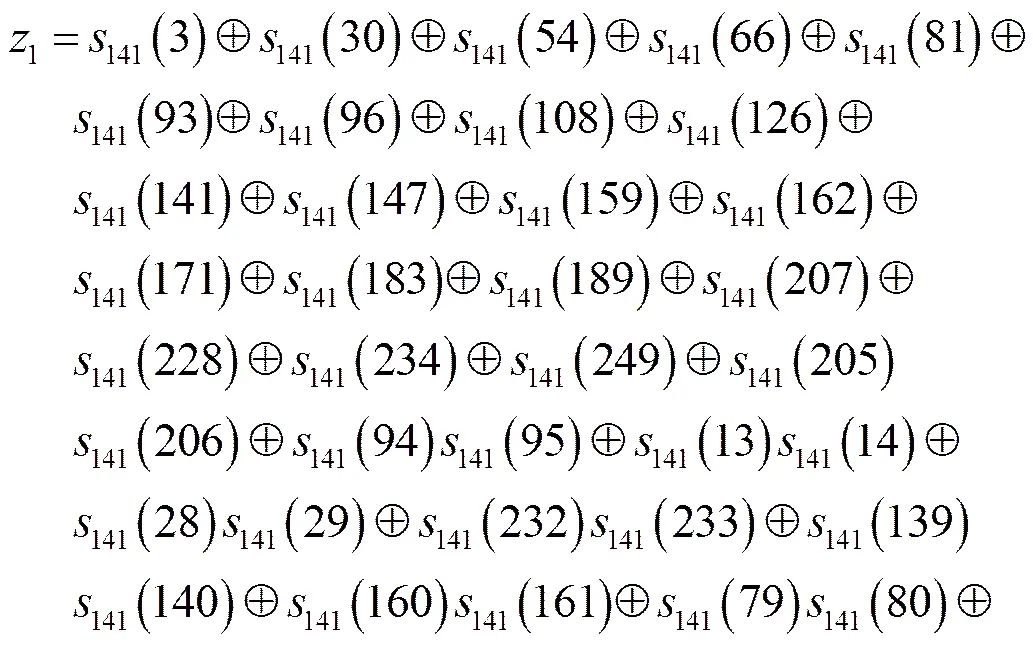
(7)
用非线性二次式
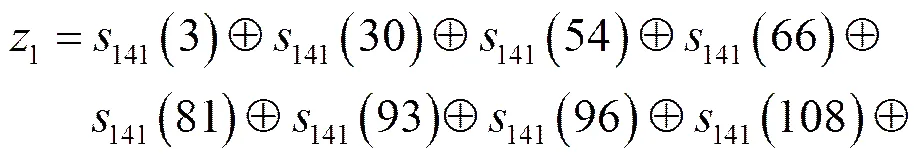
(8)

(9)
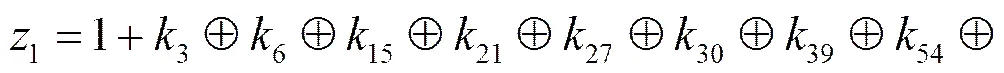
(10)
式(10)即为最终的2轮Trivium线性近似式。

表2 t1=141时z1的6个线性近似
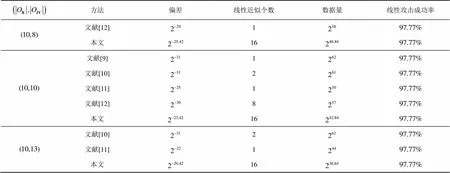
表3 结果对比
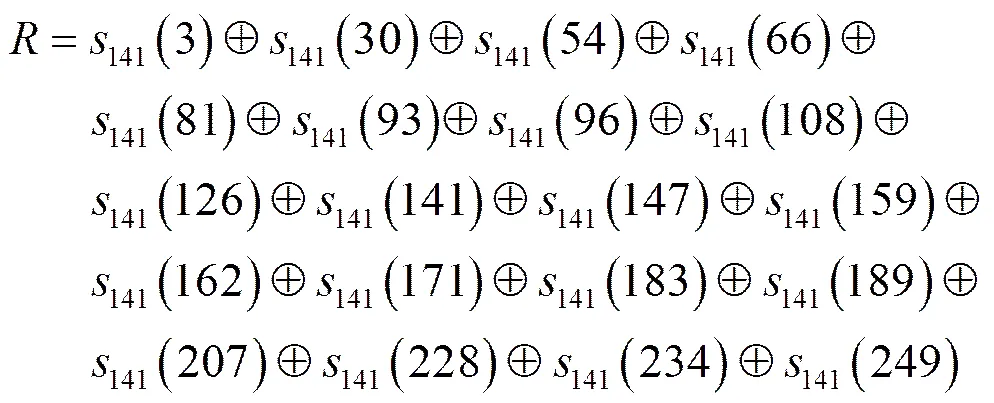
5 结束语
本文对2轮Trivium算法进行了线性逼近研究,用非线性式逼近第1轮关于密钥、和密钥流比特的表达式,给出了在某种弱密钥条件下搜索最佳线性近似式的算法,据此算法找到了16个偏差为的线性近似式,使对2轮Trivium算法进行多线性攻击的数据量降低为文献[10]所需数据量的。需要进一步研究的问题:一是算法1的时间复杂度和存储复杂度有待降低;二是能否找到2轮Trivium个数更多、偏差更大的线性近似式;三是如何利用上述思想方法对更多轮数的Trivium算法进行线性分析。
[1] CANNIÀRE C, PRENEEL B. Trivium specifications [EB/OL]. http://www.ecrypt.eu.org/stream/p3ciphers/trivium/trivium_p3.pdf, 2007.
[2] MAXIMOV A, BIRYUKOV A. Two trivial attacks on Trivium[C]// c2007:36-55.
[3] DINUR, SHAMIR A. Cubic attacks on tweakable black box polynomials[C]//Advances in Cryptology-EUROCRYPT 2009. c2009: 278-299.
[4] STANKOVSKI P. Greedy distinguishers and nonrandomness detectors[C]//INDOCRYPT 2010. c2010: 210-226.
[5] HOJSÍK M, RUDOLF B. Differential fault analysis of Trivium[C]// FSE 2008. c2008: 158-172.
[6] HU Y P, GAO J T, LIU Q, et al. Fault analysis of Trivium[C]//Designs, Codes and Cryptography. c2011: 289-311.
[7] AVIJIT D, GOUTAM P. Deterministic hard fault attack on trivium[C]//Advances in Information and Computer Security. c2014: 134-145.
[8] PRAKASH D, AVISHEK A. Improved multi-bit differential fault analysis of trivium[C]//Progress in Cryptology. c2014: 37-52.
[9] TURAN M S, KARA O. Linear approximations for 2-round Trivium[C]//Workshop on the State of the Art of Stream Cipher (SASC2007). Bochum, c2007: 22-31.
[10] 贾艳艳, 胡予濮, 杨文峰, 等. 2轮Trivium的多线性密码分析[J]. 电子与信息学报, 2011, 33(1): 223-227.
JIA Y Y, HU Y P, YANG W F, et al. Linear cryptanalysis of 2-round Trivium with multiple approximations[J]. Journal of Electronics & Information Technology, 2011, 33(1): 223-227.
[11] 孙文龙, 关杰, 刘建东. 针对简化版Trivium算法的线性分析[J].计算机学报,2012,35(9): 1890-1896.
SUN W L, GUAN J, LIU J D. Linear cryptanalysis of simplified Trivium[J]. Chinese Journal of Computers, 2012,35(9): 1890-1896.
[12] 欧智慧, 赵亚群. 2轮Trivium的线性逼近研究[J].计算机工程,2013,39(11): 31-34.
OU Z H, ZHAO Y Q. Study on linear approximation of 2-round Trivium[J]. Computer Engineering, 2013,39(11): 31-34.
[13] 李世取, 曾本胜, 廉玉忠, 等.密码学中的逻辑函数[M].北京:中软电子出版社,2003: 254-255.
LI S Q, ZENG B S, LIAN Y Z, et al. Logical functions in cryptography[M]. Beijing: Software and Electronic Press, 2003: 254-255.
[14] DOUGLAS R, STINSON. 密码学原理与实践[M]. 北京:电子工业出版社,2010: 123-124.
DOUGLAS R. STINSON. Cryptography theory and practice[M]. Beijing: Publishing House of Electronics Industry, 2010: 123-124.
[15] 丁存生,肖国镇. 流密码及其应用[M].北京:国防科学出版社,1994: 28-29.
DING C S, XIAO G Z. Stream cipher and its applications[M]. Beijing: National Defense Industry Press, 1994: 28-29.
Research on linear approximations of simplified Trivium
MA Meng, ZHAO Ya-qun
(State Key Lab of Mathematical Engineering and Advanced Computing, Information Engineering University, Zhengzhou 450001, China)
The linear approximations of simplified Trivium with the initialization of 288 clocks (2-round Trivium) was studied. An algorithm was designed to search optimal linear approximations. Moreover, a method was presented to conduct a linear approximation of 2-round Trivium by approximating the first round equation which involved the key bits,bits and the first keystream bit with a nonlinear equation. Based on this method, 16 linear approximations with the same biaswere found using proposed algorithm. Furthermore, multiple linear cryptanalysis was made on 2-round Trivium. The result shows that it can approach the same success rate withchosens, that is to say, the data complexity isof that in Turan’s scheme.
stream ciphers, Trivium, mutiple linear cryptanalysis, linear approximation
TN918.1
A
10.11959/j.issn.1000-436x.2016108
2015-06-25;
2015-12-16
信息保障技术重点实验室开放基金资助项目(No.KJ-13-009)
The Foundation of Science and Technology on Information Assurance Laboratory (No.KJ-13-009)
马猛(1986-),男,河南南阳人,信息工程大学硕士生,主要研究方向为流密码分析、概率统计在密码学中的应用。
赵亚群(1961-),女,江苏淮安人,信息工程大学教授、硕士生导师,主要研究方向为密码基础理论及概率统计应用。

