数学解题中的条件转化
余德洪
(贵州省长顺县第二中学 贵州 黔南 550700)
数学解题中的条件转化
余德洪
(贵州省长顺县第二中学 贵州 黔南 550700)
在指导学生解题和证题的过程中,常遇到题中给出的已知条件较为复杂或者比较抽象,学生不理解,很难找出已知和未知之间的相互关系,给解题和证题带来了困难,如果我们能把已知条件进行转化,使其变得简易、直观,就会大大提高解答效率,学生也容易加深印象,帮助记忆,以便提高学生对数学的学习兴趣。
一、已知条件数字化
求证:斜边和一条直角边成比例的两个直角三角形相似。

如果我们按课本的方法给学生推导证明,学生很难理解,老师的讲解也很吃力,效果也不会很好。如果我们把已知条件进行“数字”转化,学生容易理解,老师讲解也轻松许多。
设AB=5,AC=3,A'B'=10,A'C'=6
符合“斜边和一条直角边的比相等”的条件
所以Rt△ABC∽Rt△A'B'C'
老师还可以指导学生用自己喜欢的符合条件的数学加以证明。
二、已知条件的“图形化”或“表格化”。
(一)已知某工厂现有A种金属70吨,B种金属52吨,计划用这两种金属生产M、N两种型号的合金产品共80000套。已知做一套M型号的合金产品要A种金属0.6千克,要B种金属0.9千克,可获利45元。做一套N型号的合金产品要A种金属1.1千克,要B种金属0.4千克,可获得50元。若设生产N型号的合金产品x套,用这批金属生产两种型号的合金产品的总利润为y元。
1、求y与x之间的函数关系,并求出自变量x的取值范围。
2、在生产这批合金产品时,N型号的合金产品应生产多少套,该厂利润最大?最大利润是多少?
解:①根据题中的相关信息,我们把已知和未知之间进行“表格化”,设生产N型号的合金x套,则生产M型号的合金为(80000-x)套

合金型号所要金属(千克) N(x)套 M(80000-x)套 合计 A种金属 1.1x 0.6(80000-x)不大于70吨B种金属 0.4x 0.9(80000-x) 不小于52吨
根据题意,列出不等式组
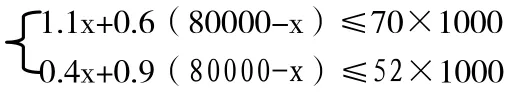
解得40000≤x≤44000
因为一套N型号合金产品可获利50元,一套M型号合金产品可获利45元,所以,y与x之间的函数关系应为
y=50x+45(80000-x)=5x+3600000 (40000≤x≤44000)
因为K=5>0,所以,y随x增大而增大。
所以当x=44000时,y最大值=5×44000+3600000=3820000(元)
即生产N型号合金44000套时,该厂可获得最大利润为3820000元。
②把已知和未知进行“图形化”。

所以有不等式组为

解得40000≤x≤44000
y与x之间的函数关系为

(二)我市A、B两树盛产芒果。A村有芒果400吨,B村有芒果100吨,现将这些芒果运到甲乙两个冷藏库储存。已知甲仓库可储存240吨,乙仓库可储存60吨,从A村运到甲乙两库的费用分别是每吨20元和25元,从B村运到甲乙两库的费分别是每吨10元30元。请设计一个方案,使芒果和运输费用最少,并求出最小费用。
解:方法1,把已知条件“图形化”
设从A村运x吨芒果到甲仓库储存,运输费用为y元

所以y=20x+25(400-x)+10(240-x)+30(x-140)

因为k=15>0,所以y随x增大而增大。
所以当x=140时,y最小值=10300(元)]
即从A村运140吨芒果到甲仓库储存时,运输费用最少,最少费用为10300元。
方法2:把已知条件进行“表格化”
设从A村运x吨芒果到甲仓库储存。

仓库产地 甲 乙 合计(吨) A村 X 400-x 400 B村 240-x 260-(400-x) 100合计(吨)240 260 500
根据已知条件,y=20x+25(400-x)+10(240-x)+30(x-140)
y =15x+8200 (140≤x≤400)结论与方法(一)一样。
三、已知条件“语言文字”化
(一)小明上周三在超市花 10元钱买了几袋牛奶,周日再去买时恰遇超市搞优惠酬宾活动,同样的牛奶,每袋比周三便宜了0.5元,结果小明只比上次多花2元钱,即比上次多买了2袋牛奶,问小明上周三买了几袋牛奶,每袋牛奶多少钱?
解:方法①,设小明上周三买牛奶x袋,根据题意可知:
A:上周三一袋牛奶的钱—周日一袋牛奶的钱=0.5
B:上周三一袋牛奶的钱=
解得x=4(袋) 10÷4=25(元/袋)
即小明上周三买牛奶4袋,每袋2.5元钱。
方法②设上周三每袋牛奶x元钱,则周日每袋牛奶为x-0.5元钱
因为周日买的袋数比上周的买的袋数多2袋
解得x=2.5(元) 与方法①结果一样。
(二)某服装厂设计了一款新式夏装,想尽快制出 8800件投放市场,服装厂有甲、乙两个制衣车间,甲车间每天加工的数量是乙车间的1.2倍,甲、乙两车间共同完成一半以后,剩下的部分由乙车间单独完成,结果共同用 20天完成任务。求甲乙两车间每天分别加工多少件?请列出方程。
有以下数量关系需要确点:
A、生产前一米的时间+生产后一米的时间=20天
B、甲车间一天生产的件数=乙车间一天生产件数的1.2倍
设乙车间一天加工x件,则甲车间一天加工1.2x件
众所周知,学生在数学学习上,要取得好的成绩,除了自己的刻苦努力以外,还必须有老师的正确指导。解题思路、解题方法的形成,需要我们当老师的在长期的教学过程中,不断的去探索、去积累、去总结、去发现,使自己的教学方法、教学水平不断的提高,不断的升华,使学生学起来轻松愉快,使他们在成才的道路上少走一些弯路,多一些捷径。