基于连续介质的裂隙岩体流固耦合数值分析

唐佳，彭振斌，何忠明



基于连续介质的裂隙岩体流固耦合数值分析

唐佳1, 2，彭振斌1，何忠明3

(1. 中南大学地球科学与信息物理学院，湖南长沙，410083；2. 中国电建集团中南勘测设计研究院有限公司地质工程处，湖南长沙，410007；3. 长沙理工大学交通运输工程学院，湖南长沙，410076)

基于库区水位涨落或暴雨入渗，经过演变易造成滑坡，研究渗透压作用下裂隙损伤效应对渗透张量的影响，通过理论推导，提出裂隙岩体渗流场与损伤场耦合的分析模型；以湖北潘口水电站进水口边坡为研究对象，建立基于连续介质的裂隙岩体流固耦合渗流数值计算分析方法。研究结果表明：边坡在开挖过程中变形以卸荷回弹变形为主，回弹变形范围随开挖逐级增大，各级边坡开挖对邻级边坡变形的影响最显著，对较远坡段的影响逐步减弱；边坡开挖面基本处于小拉应力状态，边坡浅表层拉应力区分布范围及量值均很小；边坡全部开挖完成后，边坡的塑性区主要沿近坝的开挖马道外缘分布，分布范围小，在表层岩体内；裂隙岩体流固耦合模型的三维数值计算能够较真实地模拟边坡开挖过程位移场、应力场、塑性区、拉应力区的分布规律。

滑坡；渗透压力；连续介质；流固耦合；数值计算

水电站库区水位涨落或暴雨入渗易造成滑坡。通过对水库滑坡进行实测分析，中村浩之等[1]认为造成水库滑坡的主要因素有水库浸水、水库水位急剧下降与降雨3个方面；王思敬等[2]根据水库滑坡产生的原因将其划分为天然滑坡和在水岩作用影响下的滑坡2类；王士天等[3]则认为，当库水位已达到敏感水位或者库水位消落且处在快速消落期时很容易发生滑坡。唐晓松等[4]发现水库滑坡不同于一般山体滑坡, 其稳定性受水位波动的影响十分明显。严福章等[5]通过对清江隔河岩水库坪滑坡进行研究，提出在水库蓄水后，该滑坡发生了较长的缓慢变形，其根本原因是水库蓄水产生的材料和水力学效应共同作用以及滑带抗剪强度在滑体变形后降低，产生了应变软化作用。张有天等[6]通过对60座水库滑坡进行统计后指出，85%的滑坡在建设期、蓄水期或者在水库存工程完工之后2 a内发生。裂隙岩质岸坡位移速率随着库水位上涨不断加大，在库水位降低时不断减小甚至会停止。李佳伟等[7]通过岩石力学试验，揭示了砂板岩岩体的高空隙水压力效应，建立了主要力学参数预测模型。可见，为了探讨地质灾害的真正原因，必须从岩石水力学的角度对岩体的渗透规律和损伤力学响应进行研究，并采取流固耦合分析法对裂隙岸坡失稳机制进行分析。湖北潘口水电站库岸大部分为白云母石英片岩，岩性较软弱，岩石风化较强烈，加之区域构造活动频繁，节理、构造发育，易产生顺层滑坡和沿结构面与层面组合的滑坡，为此，本文作者以潘口水电站库岸为研究对象，同时考虑静水压力和动水压力的影响，提出基于等效连续介质的裂隙岩体流固耦合渗流分析数值模型，同时对考虑渗流与应力相互作用下进水口边坡进行数值分析，研究相应部位边坡的位移场、应力场、塑性区、拉应力区分布规律，系统评价边坡的稳定性。

1 裂隙岩体连续介质渗流模型

1.1 等效渗透系数的计算

同理，用表示裂缝法线测线的长度，表示裂缝的数目，则岩体线密度d为

(2)

基于岩块的渗透系数m、宽度m及裂隙面的渗透系数为f、宽度c，由达西定律得到岩体的渗流量：

(4)

式中：为岩体宽度；f为单条裂隙宽度。

则岩块宽度为

可得岩体等效渗透系数K：

(6)

垂直面其等效渗透系数为

则

(8)

采用线连续性系数将裂隙的实际渗透系数t修正为

K和K又可以表示为：

(10)

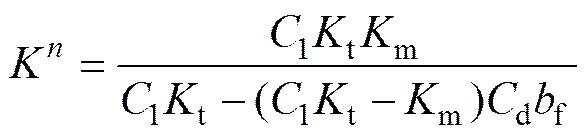
K和K反映了岩体渗透特性的各向异性。假定裂纹的角度为，则等效二阶张量的渗透率为：

(12)

(14)

由此获得了裂隙岩体二维等效渗透系数。

1.2 渗透压作用下岩体的渗透系数

考虑岩体受到渗透水压力和应力共同耦合作 用[8]，且其渗透系数一般随应力环境的改变而变化，渗透系数张量可表示为

式中：为裂隙半径；为裂隙隙宽；为裂隙法向矢量。相应渗透量为

(16)

(17)

(＞1) (18)

1.3 裂隙岩体流固耦合机理

据文献[9−10]，假定岩体水头值为，则静水压为

(20)

当单裂隙水平分布时，裂隙中的动水压为

(22)

1.4 岩体渗流场和应力场耦合数学模型的建立

式中：岩体的等效渗透系数为应力场的函数，即；s为贮水率；为岩体的渗流区间；和分别为初始时刻及1上的水头分布；1和2分别为已知水头边界及流量边界；为2边界上法向量；为2上的流量分布。岩体的平衡方程为

式中：f和f为分别为和的岩体质量力。岩体的几何方程为

(26)

岩体的本构方程为

岩体的应力边界条件为

1.5 耦合方程的建立

同时在裂隙岩体渗流中考虑应力对渗流的影响，引进耦合方程：

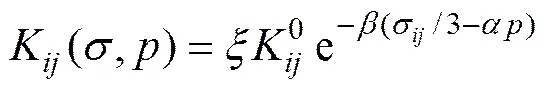
2 流固耦合数值计算

在模拟岩体的流固耦合机理时，视流体满足Biot方程，依据Darcy定律在岩体孔隙介质中的流动[11−12]，得以下几个主要方程。

2.1 平衡方程

岩体渗流平衡状态时，

(31)

液体质量平衡方程为

动量平衡方程为

(33)

其中：g为重力加速度在方向的分量；，为体积密度；s和w分别为固体和液体密度；(1−)s为岩石干密度即d。

2.2 运动方程

用达西定律描述流体的运动[13]：

式中：为介质的渗透系数；f为流体密度：g为重力加速度在方向的分量；x为方向的坐标分量。

2.3 本构方程

孔隙介质本构方程的增量形式为

无形的劲气开始在天问大师和萧飞羽身前流转，渐渐地，劲气将血醒的尘土带着飞了起来。天问大师双手如挽重物缓缓提到胸前，紧接着向外一翻，一股强大的劲气应手而出。萧飞羽没有作势，右掌随意一翻。“轰！”一声闷响，尘土被激起、飞射、旋转、坠落。

2.4 液体响应方程

完全饱和时，=1，响应方程为

同时有

(37)

当＜1时，响应方程为

相对渗透性与饱和度的关系为

(39)

对于小变形响应方程为

(41)

2.5 相容方程

应变与速度的关系为

式中：u为介质的速度。

2.6 边界条件

耦合计算可采用以下透水边界条件[14]：

式中：n为边界外法线方向流速分量；为渗漏系数；e为渗流出口处的孔隙水压力。

3 边坡应力变形有限元分析

3.1 边坡岩体工程特性

潘口水电站岸塔式进水口布置在左岸坝前。边坡地形较陡，大部分地段基岩裸露，岩性为白云母石英片岩夹云母片岩，局部含炭质条带，富含石英脉；缓坡部位分布有残、坡积物。岩层片理走向为320°~330°/ NE∠40°~55°，发育的节理主要有280°~290°/ SW∠40°~60°，345°~355°/SW∠40°~60°和60°~70°/ SE∠40°~70°共3组。边坡平面布置及其相互关系如图1所示(比例尺为1:500，图中数字1~6代表剖面编号)，边坡岩体的物理力学参数取值见表1。

3.2 有限元计算模型及边界条件

采用的自主二次开发的有限元软件EVP3D进行有限元建模及计算。模型的建造遵循“点→线→面→体”自下而上的建模技术。模型中采用六面体单元和部分四面体退化单元模拟。模型共剖分单元18 194个，结点14 932 个，其中开挖单元2 581 个，如图2所示。边坡开挖后的模型如图3所示。考虑模型所处的地形地貌条件及边坡荷载方向，模型边界条件，和向分别取法向支座约束。

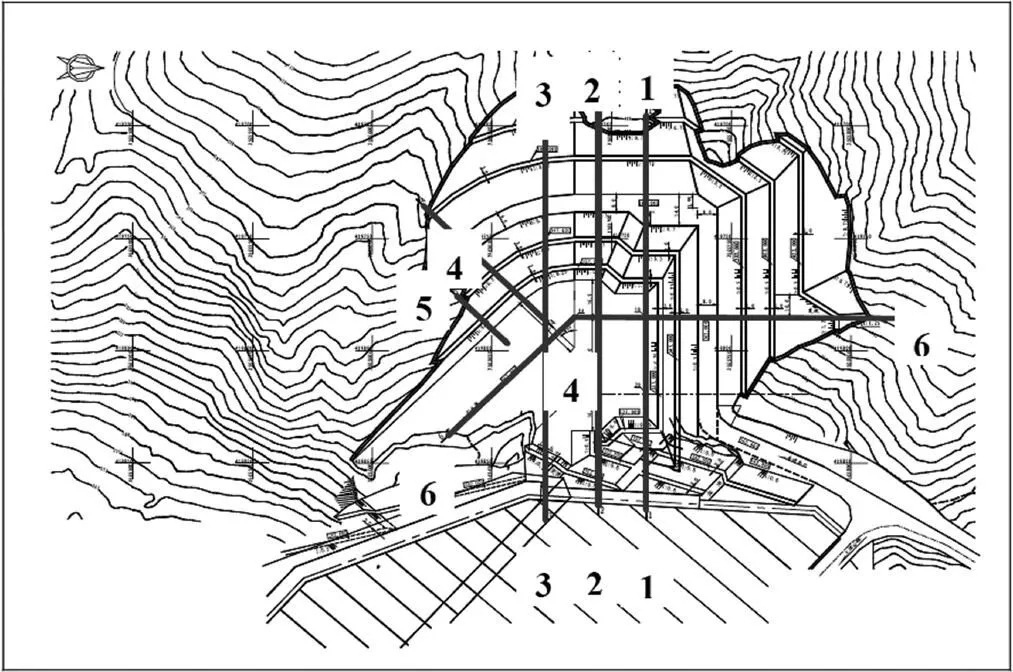
图1 进水口边坡平面图

表1 边坡岩体力学参数

图2 开挖前的进水口边坡三维有限元模型

3.3 计算荷载及施工过程模拟

边坡计算荷载包括岩体自重应力场、开挖荷载等。施工期开挖荷载是最主要的计算荷载，其计算式为[15]

式中：{}为开挖荷载向量；[]为单元几何矩阵；[]为形函数矩阵；{}为初始应力；{}为体积力向量；E为开挖单元集合。本次计算在初始地应力场(主要考虑自重应力场)模拟的基础上，按307，327，347，362，382，402和422 m共7个开挖量模拟进水口边坡的开挖过程。

图3 开挖后的进水口边坡三维有限元模型

Fig. 3 Three-dimensional finite element model of intake-slope after excavation

3.4 位移成果分析

进水口边坡在开挖过程中的整体位移云图如图4所示。为了分析进水口边坡开挖过程中的变形规律，在边坡开挖坡面上选取13 个关键点，如图5所示。部分关键点(1，3，5，7，9，11和13)随边坡开挖的位移过程曲线如图6所示。

从图4~6可看出进水口边坡在开挖过程中具有如下变形规律：

1) 边坡在开挖过程中，各开挖坡面上的变形以卸荷回弹变形为主，回弹变形的方向垂直向上，并略指向山体内部，边坡完全开挖后产生的最大变形出现在307 m高程的基坑中央约14.06 mm处。

2) 边坡各坡段在开挖过程中产生的变形增量与开挖量有关，开挖量越大，边坡的变形增量也越大，且高高程坡面相比低高程坡面变形小。

3) 从开挖产生变形的变化过程可知开挖引起的回弹变形范围，随着开挖的深入而逐级增大；各级边坡变形受邻级边坡开挖的影响最严重，受较远边坡开挖的影响则逐层减弱；而开挖坡段受后断边坡开挖影响边坡变形递增，最终则趋向平稳。

(a) 开挖步1; (b) 开挖步3; (c) 开挖步5; (d) 开挖步7

图5 进水口边坡关键点位置示意图

关键点：1—K1; 2—K3; 3—K5; 4—K7; 5—K9; 6—K11; 7—K13。

3.5 应力计算成果分析

边坡在开挖过程中3−3 剖面第一主应力云图如图7所示，第三主应力云图如图8所示，全部开挖完成后的拉应力区分布如图9所示。计算分析结果表明：边坡面在开挖过程中基本上处于小拉应力状态，且处于表层岩体之中深度约5 m以内，这种应力状态整体上对边坡稳定性影响很小；每一步开挖产生的拉应力基本上都处于表层岩体中，随开挖量增大逐渐减小但变化不大，后2步(即327 m和307 m)开挖在开挖马道坡面上产生很小范围的压应力区；每一步开挖产生的压应力也基本上都处于表层岩体中，全部开挖完成后小主应力分布在307~402 m 之间的坡段上，最大值约为2.5 MPa，出现在307 m高程基坑内侧靠近坡脚处。

图7 3−3剖面第7步开挖第一主应力云图

图8 3−3剖面第7步开挖第三主应力云图

图9 进水口边坡完全开挖后拉应力区分布

3.6 塑性区分布

边坡开挖完成后的整体塑性区如图10所示。

分析图10可知：边坡的塑性区主要沿近坝马道外缘分布，在高程402，382和362 m马道外缘分布较集中，高程327 m马道也有小范围分布。总体上，开挖引起的塑性区范围较小，深度在表层岩体8 m之内，对开挖边坡整体稳定性影响不大。针对边坡浅表的塑性变形，应及时进行浅表层的锚杆支护，以确保边坡局部稳定。

图10 进水口边坡完全开挖后塑性区分布

4 结论

1) 考虑渗透压作用下裂隙损伤效应对渗透张量的影响，通过理论推导，提出了裂隙岩体渗流场与损伤场耦合的分析模型。

2) 建立了基于等效连续介质的裂隙岩体流固耦合渗流数值计算分析方法。对潘口水电站进水口边坡进行模拟验证，结果表明边坡在开挖过程中变形以卸荷回弹变形为主，范围随开挖逐级增大；各级边坡开挖对邻级边坡变形的影响最显著，对较远坡段的影响逐步减弱；边坡开挖面基本处于小拉应力状态，浅表层拉应力区分布范围及量值均很小。边坡全部开挖完成后，边坡的塑性区主要沿近坝的开挖马道外缘分布，分布在表层岩体范围内。

3) 采用裂隙岩体流固耦合模型的三维数值计算能较真实地模拟边坡开挖过程位移场、应力场、塑性区、拉应力区的分布规律，相对于传统的二维极限平衡分析，其对工程设计与施工具有重要的指导意义。

参考文献：

[1] 中村浩之, 王恭先. 论水库滑坡[J]. 水土保持通报, 1990, 10(1): 53−64. Nakamura Hiroyuki, WANG Gongxian. Creep on reservoir landslide[J]. Bulletin of Soil and Water Conservation, 1990, 10(1): 53−64.

[2] 王思敬, 马凤山, 杜永康. 水库地区的水岩作用及其地质环境影响[J]. 工程地质学报, 1996, 4(3): 1−9. WANG Sijing, MA Fengshan, DU Yongkang. On the rock-water interaction in reservoir areas and its geoenvironmental effect[J]. Journal of Engineering Geology, 1996, 4(3): 1−9.

[3] 王士天, 刘汉超, 张悼元, 等. 大型水域水岩相互作用及其环境效应研究[J]. 地质灾害与环境保护, 1997, 8(1): 69−89. WANG Shitian, LIU Hanchao, ZHANG Daoyuan, et al. Study on water rock interaction and its environmental effect in large water area[J]. Journal of Geological Hazards and Enviroment Preservation, 1997, 8(1): 69−89.

[4] 唐晓松, 郑颖人, 唐辉明, 等. 水库滑坡变形特征和预测预报的数值研究[J]. 岩土工程学报, 2013, 35(5): 940−947. TANG Xiaosong, ZHEN Yingren, TANG Huiming, et al. Numerical researches on deformation characteristics and prediction of reservoir landslides[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(5): 940−947.

[5] 严福章, 王思敬, 徐瑞春. 清江隔河岩水库蓄水后茅坪滑坡的变形机理及其发展趋势研究[J]. 工程地质学报, 2003, 11c(1): 15−24. YAN Fuzhang, WANG Sijing, XU Ruichun. Creeping deformation of the Maoping landslidean ditssbabm in the Geheyan reservoir on the Qingjiang river[J]. Journal of Engineering Geology, 2003, 11c(1): 15−24.

[6] 张有天. 岩石水力学与工程[M]. 北京: 中国水利水电出版社, 2005: 11−47. ZHANG Youtian. Rock hydraulics and engineering[M]. Beijing: China Water and Power Press, 2005: 11−47.

[7] 李佳伟, 徐进, 王璐, 等. 砂板岩岩体力学特性的水岩耦合试验研究[J]. 岩土工程学报, 2013, 35(3): 599−604. LI Jiawei, XU Jin, WANG Lu, et al. Water-rock coupling tests on mechanical properties of sandy slate rock mass[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(3): 599−604.

[8] 赵延林, 曹平, 赵阳升, 等. 双重介质渗流场−应力场−温度场耦合模型及三维数值研究[J]. 岩石力学与工程学报, 2007, 26(增2): 4024−4031. ZHAO Yanlin, CAO Ping, ZHAO Shengyang, et al. Dual media model for thermo-hydro-mechanical coupling and 3D numerical simulation[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Suppl 2): 4024−4031.

[9] 易顺民, 朱珍德. 裂隙岩体损伤力学导论[M]. 北京: 科学出版社, 2005: 9−37. YI Shunmin, ZHU Zhende. Introduction to damage mechanics of fractured rock mass[M]. Beijing: Science Press, 2005: 9−37.

[10] 朱维申, 张强勇. 节理岩体脆弹性断裂损伤模型及其工程应用[J]. 岩石力学与工程学报, 1999, 18(3): 245−249. ZHU Weishen, ZHANG Qiangyong. Fracture damage model of jointed rock mass and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(3): 245−249.

[11] 杨延毅. 节理裂隙岩体损伤断裂力学模型及其在岩体工程中的应用[D]. 北京: 清华大学土木工程学院, 1990: 13−41. YANG Yanyi. Damage fracture mechanics model of Joint fracture and application[D]. Beijing: Tsinghua University. School of Civil Engineering, 1990: 13−41.

[12] KEMENY J M, COOK N G W. Crack models for the failure of rocks in compression,constitutive laws for engineering materials[M]. New York: Elsevier, 1987: 879−887.

[13] 赵延林. 裂隙岩体渗流−损伤−断裂耦合理论及应用研究[D]. 长沙: 中南大学资源与安全工程学院, 2009: 16−48. ZHAO Yanlin. Coupling theory of seepage−damage−fracture in fractured rock masses and application[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2009: 16−48.

[14] 谢东海, 冯涛, 赵延林, 等. 裂隙煤岩体的流固耦合精细模型[J]. 中南大学学报(自然科学版), 2014, 45(6): 2014−2020. XIE Donghai, FENG Tao, ZHAO Yanlin, et al. Fluid-solid coupling detailed model of rock-coal mass[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 2014−2020.

[15] 陈涛, 吴旭敏, 陈晓江. 锦屏二级上游调压室洞室群开挖支护动态设计与研究[J]. 岩石力学与工程学报, 2014, 33(Sl): 2593−2599. CHEN Tao, WU Xumin, CHEN Xiaojiang. Dynamic design and research on excavationg and support design of upper surge chamber caverns of Jinping II hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sl): 2593−2599.

(编辑 陈灿华)

Numerical analysis of fluid-solid coupling in fractured rock mass based on continuous medium

TANG Jia1, 2, PENG Zhenbin1, HE Zhongming3

(1. School of Geosciences and Info−Physics, Central South University, Changsha 410083, China;2. Geological Engineering Department, Powerchina Zhongnan Engineering Co. Ltd., Changsha 410007, China;3. School of Traffic and Transportation Engineering, Changsha University of Science and Technology, Changsha 410076, China)

Considering that reservoir water level fluctuation or rainstorm infiltration will cause landslide, the effect of crack damage effect on the permeability tensor was studied. Through theoretical deduction, the analysis model of coupling of seepage field and damage field in fractured rock mass was put forward. Then taking the Hubei Pankou hydropower station intake-slope as object, a numerical analysis method of fluid solid coupling seepage flow in fractured rock mass was established based on the equivalent continuous medium. The results show that deformation of slope is mainly based on unloading springback during excavation; deformation range increases with the increase of excavation; the influence of slope excavation at all levels on the deformation of adjacent level slope is the most significant; distance slope section is gradually weakened. After the completion of the excavation, slope of the plastic zone is mainly layed along the near dam outer edge of the distribution, and the distribution range is small and in the surface of rock mass. Three-dimensional numerical calculation of fluid solid coupling model of fractured rock mass can simulate the distribution law of the displacement field, stress field, plastic zone and tensile stress zone of the slope excavation process.

landslide; osmotic pressure; continuous medium; fluid−solid coupling; numerical calculation

10.11817/j.issn.1672-7207.2016.11.025

TU457

A

1672−7207(2016)11−3800−08

2016−01−10；

2016−03−22

国家自然科学基金资助项目(51508042) (Project(51508042) supported by the National Natural Science Foundation of China)

唐佳，博士研究生，工程师，从事地质工程、岩土工程研究；E-mail: csutangjia@126.com