电动滑板桥轻量化优化设计
撰文/厦门大学嘉庚学院 陈毅龙 林育兹 郑伟
电动滑板桥轻量化优化设计
撰文/厦门大学嘉庚学院 陈毅龙 林育兹 郑伟
本文通过SolidWorks建立参数化的电动滑板桥三维模型,导入ANSYS Workbench中进行静力学分析,根据分析的应力、应变结果,进行拓扑优化,得到合理的拓扑结构。结合拓扑优化结果和工程经验,以质量最小为目标函数,强度为约束条件,进行滑板桥尺寸优化设计,在保证滑板桥强度前提下,优化后的滑板桥比原滑板桥质量减少了33.33%,取得良好的轻量化效果。该优化方法为电动滑板车轻量化设计提供一种思路。
一、引言
电动滑板是在传统滑板上加装一套电控驱动系统,它通过遥控器控制专用电机转向和转速,经传动机构带动滑板的轮子转动,从而使滑板行进,实现代步的作用,其作为一款新型的代步工具,深受年轻人喜爱,成为一种流行趋势。电动滑板桥是连接轮子与板面的支架结构,承担轮子与板面之间动力传递。目前,国内电动滑板桥均沿用了传统滑板桥的结构设计,但由于电动滑板不需要做出传统滑板诸如起跳、翻转之类的动作,受力情况单一,传统滑板桥结构便显得较为笨拙,强度上存在较大冗余,因此去除桥结构多余材料,减轻重量变得尤为重要。国内对电动滑板研究主要集中在电控系统和板面材料选择上,针对桥结构优化鲜有研究。
针对以上情况,本文建立了电动滑板桥有限元模型,通过静力学分析,得到电动滑板桥的应力、应变结果,根据分析结构,进行拓扑优化,得到合理的拓扑结构。随后,以质量最小为目标函数,强度为约束条件,进行电动滑板桥尺寸优化设计,在保证滑板桥强度前提下,取得了良好的轻量化效果。该研究为电动滑板桥结构设计优化提供一种思路,对减轻重量、节约成本具有重要意义。
二、电动滑板桥结构应力分析
1.电动滑板桥有限元模型
所选电动滑板桥实物,如图1所示,材质为结构钢,重量为0.66kg。根据电动滑板桥实物,在SolidWorks中建立三维模型,然后通过专用接口将SolidWorks模型无缝导入ANSYS Workbench中。在ANSYS Workbench中对其进行网格划分,划分后网格的主要参数为:网格形状六面体,网格大小3mm,网格数28490个,节点数43633个。建立起的有限元模型,如图2所示。

图1 所选电动滑板桥实物图

图2 电动滑板桥有限元模型
2. 电动滑板桥静力学分析
桥两端通过滚动轴承与车轮连接,中部凹坑处通过螺栓与滑板连接,该处承受来自滑板的主要压力,顶部半球结构通过球面副与滑板连接,该处结构用于转向之用,同时承受一部分压力。电机带动车轮旋转,通过滚动轴承推动桥行进,该桥不做转动,可忽略对剪切力的分析。滑板起动瞬间,桥左右两端将受到轮子传来的水平推动力,考虑到起动瞬间并非常规状态,同时滑板匀速行驶过程中该力为零,将模型简化,本文只对静态下受力情况进行分析。
当人静止的站在滑板上时,受力分析如图3所示。人和滑板自重合计100kg,重力G为1000N,每根桥竖直方向承重F为500N,因桥与地面水平方向成45°,所以桥承受来自板面的压力N约为700N。取左右2端轴承连接处为固定端,得到载荷模型,如图3所示。其中A处紫色部分为固定约束,B处红色部分为施加在桥上的载荷。

图3 电动滑板桥载荷模型图
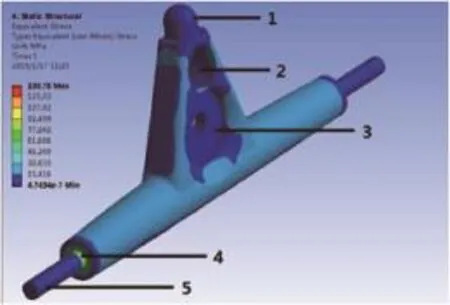
图4 最大等效应力分析云图

图5 总变形量分析云图
根据材料力学第四强度理论,分析计算后的最大等效应力云图如图4所示,总变形量如图5所示。
由图5可见,应力最大处主要集中在桥左右2端的位置4处,该处截面形状的突变引起了应力集中现象,最大等效应力达到了138.75MP。在该模型下,滑板桥等效应力小于45钢屈服极限355MP,安全系数为:
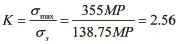
该安全系数大于塑性材料结构钢常用的1.2~2.5安全系数,因此该滑板桥满足强度要求。
由图6可知,最大变形处发生在红色半球结构上,变形量为0.15mm,该变形量对于间隙配合的球面副结构没有影响,因此该轮桥可正常使用。
由图5可见,大多数位置最大等效应力较小,其中位置1、2、3、5处最大等效应力很小,在15.42MP以下,整根桥应力分布不均,材料存在大量浪费现象,额外的重量也影响动力性能。由于电动滑板的工作情况较单一,原桥结构强度冗余较大,无法满足电动滑板车设计要求,因此对该桥进行拓扑优化设计,去除掉多余的材料,重新设计结构。
三、电动滑板桥结构拓扑优化
1.拓扑优化理论基础
拓扑优化的目的是寻求结构的刚度在设计空间最佳的分布形式,或在设计域空间需求结构最佳的传力路线,以优化结构的某些性能或减轻结构的重量。拓扑优化主要应用于概念设计阶段,得到最佳的材料分布,避免设计的盲目性,经拓扑优化后设计方案再经形状和尺寸优化以得到最优方案。
针对连续体拓扑优化,目前有变厚度法、均匀化理论和变密度法等诸多理论。本文中采用变密度法,其本质上是一种{0,1}离散变量的组合优化问题,因此可建立如下数学模型:

式中,xi为设计变量,代表离散单元相对密度,取值在[xmin,1]之间连续值,n代表设计变量个数。K为总刚度矩阵,U为结构的位移向量,F为结构所受的外力向量,V为结构体积。
2. 电动滑板桥拓扑优化设计
以最大等效应力为约束条件,质量为目标函数,通过ANSYS Workbench中的Shape Optimization功能对所选桥进行优化,选择Target Reduction值为30%,优化后结果如图6、图7所示。

图6 桥拓扑优化外貌云图
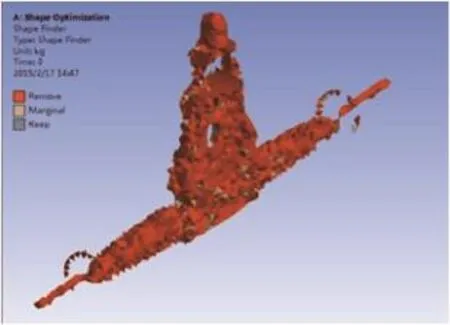
图7 桥拓扑优化去除云图
图6为Shape Optimization给出的优化外貌图,其中橙色部分为可去除部分,米黄部分为边界区域,灰色部分为保留部分。图7为上限等值面云图,表示该轮桥内部可去除的部分。
综合分析图4~7,对原滑板桥做形状优化处理。
(1)整体可去除量很大,达30%以上,考虑到内部掏空方式在制造上较难实现,主要采取从外部挖除材料方法进行优化设计。
(2)图6中1处圆孔可进一步扩大。
(3)2处为连接处,因配合要求,中心形状不变,周边一圈挖除多余材料。
(4)3处有1过渡圆角,经Design Exploration模块参数化分析后可知,圆角几乎不会影响最大等效应力,但会影响最大形变量,随着圆角增大形变趋小。
(5)4处考虑到与轴承的配合,受到尺寸约束,不做车削外径处理。
(6)5处考虑到加工难度和成本,不做镗孔去除处理。
根据以上几点,先在SolidWorks中对该桥形状做修改,随后导入ANSYS中进行静力学分析,经过几十次修改和比较,得到新形状,新形状的最大等效应力和总变形量如图8、9所示。
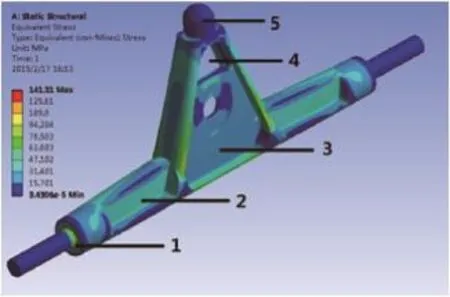
图8 形状优化后最大等效应力云图

图9 形状优化后总变形量云图
图8中,2、3、4处挖除多余材料,1、5处不变,整体应力分布较原结构均匀。应力最大处位于1处截面突变处,为141.31MP,略大于优化前的138.75MP。重量为0.46kg,仅为优化前质量的69.79%。最大变形量0.34mm,虽较优化前小幅提升,但仍然很小,对正常使用没有影响。
四、电动滑板桥尺寸优化设计
1.尺寸优化理论基础
尺寸优化是拓扑和形状固定条件下一种参数化的技术,以几何尺寸为设计变量,寻找最优参数组合的一种方法。优化设计有3要素,即设计变量、目标函数和约束条件。设计变量是发生改变从而提高性能的一组参数;目标函数要求最优的设计性能,是关于设计变量的函数;约束条件是对设计的限制,是对设计变量和其他性能的要求。尺寸优化数学模型如下:

式中,f(x)为目标函数,X为设计变量,fi(x)为约束条件,x2为设计变量约束。
2.四轮电动滑板车轮尺寸优化
根据尺寸优化数学模型,选取图8中2处的挖除深度为变量X,质量为目标函数f(x),等效应力为约束条件fi(x),经过Design Exploration模块求解后,获得参数响应图,如图10、11所示。
图10中,横坐标表示挖除深度,纵坐标表示最大等效应力,最大等效应力随着挖除深度增加而变大。图11中,横坐标表示挖除深度,纵坐标表示桥的质量,质量随着挖除深度增加而减小。
取安全系数2.5,则允许最大等效应力为142MP,取该值为约束条件,优化后的目标质量为0.44kg。滑板桥优化前后最大等效应力、质量对比如表所示。

图10 最大等效应力参数响应图

图11 质量参数响应图
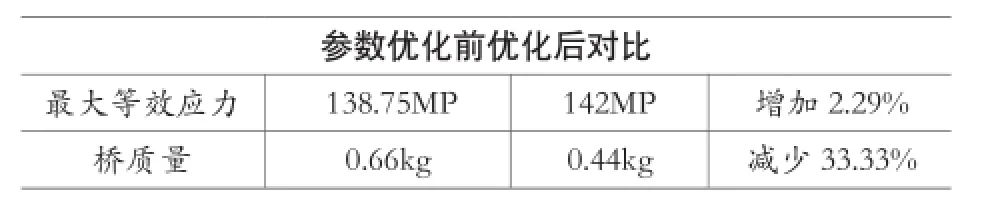
表 优化前后最大等效应力、质量对比情况
由表可知,通过优化设计,在满足强度前提下,将质量减少了33.33%,获得了良好的轻量化效果。
五、结语
根据某电动滑板桥实物,建立有限元模型,通过拓扑优化,将冗余材料去除,设计出新的结构,解决了应力分布不均的问题并进行尺寸优化。优化结果表明,在满足强度的情况下,桥质量减少了33.33%,获得了良好的轻量化效果。通过轻量化优化,减少原滑板桥质量、提高材料利用率、降低生产成本、提高动力性能,使该电动滑板更具市场竞争力。该优化设计为电动滑板桥改进提供借鉴,具有工程实际意义。

