库水位骤降对黏土心墙坝坝坡稳定的影响分析

王资欢　张晓峰

(1.河南省水利第二工程局， 河南 郑州　450016；2.北京国泰节水发展股份有限公司， 北京　100053)



库水位骤降对黏土心墙坝坝坡稳定的影响分析

王资欢1张晓峰2

(1.河南省水利第二工程局， 河南 郑州450016；2.北京国泰节水发展股份有限公司， 北京100053)

坝坡稳定是土石坝设计的重要内容,在极端工况条件下，坝体内孔隙水压力常不能很快消散，较高的孔隙水压力和渗透力会使上游坝坡具有下滑趋势，甚至酿成滑坡事故。鉴于此，应用三维非稳定饱和-非饱和渗流有限元法建立大黑箐水库枢纽区三维有限元模型，对极端工况条件下坝体的非稳定渗流场进行模拟分析。结果表明，1d内库水位自校核洪水位骤降至正常蓄水位，不会对心墙的稳定造成不利影响。

土石坝； 心墙； 非稳定渗流； 有限元法； 渗透坡降

坝坡稳定是土石坝设计的重要内容。当库水位骤降时，坝体内孔隙水压力常常不能很快消散，浸润线高于坡外库水位，较高的孔隙水压力和渗透力会使上游坝坡具有下滑趋势，甚至酿成滑坡事故[1-3]。1979年，湖北省狮子岩土石坝，因发现漏水而决定放空水库，上游坝坡受库水位骤降影响(v=1.60m/d)产生滑坡[4]。因此，在实际工程中进行土石坝上游坝坡稳定分析，以防止因库水位下降过快而导致滑坡事故发生显得尤为重要。鉴于此，本文以大黑箐水库黏土心墙坝为研究对象，应用三维非稳定饱和-非饱和渗流有限元法对该坝在极端工况下(v=4.16m/d)的非稳定渗流场进行模拟分析，探讨水位骤降对该坝上游坝坡稳定的影响。

1　非稳定饱和-非饱和渗流基本原理

假定达西定律同样适用于非饱和渗流情况，则非饱和渗流基本微分方程可以采用与饱和渗流相同的方法推导得到[5]。非稳定饱和-非饱和渗流基本微分方程：

(1)

式中hc——压力水头；

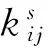
ki3——饱和渗透系数张量中仅和第3坐标轴有关的渗透系数值；

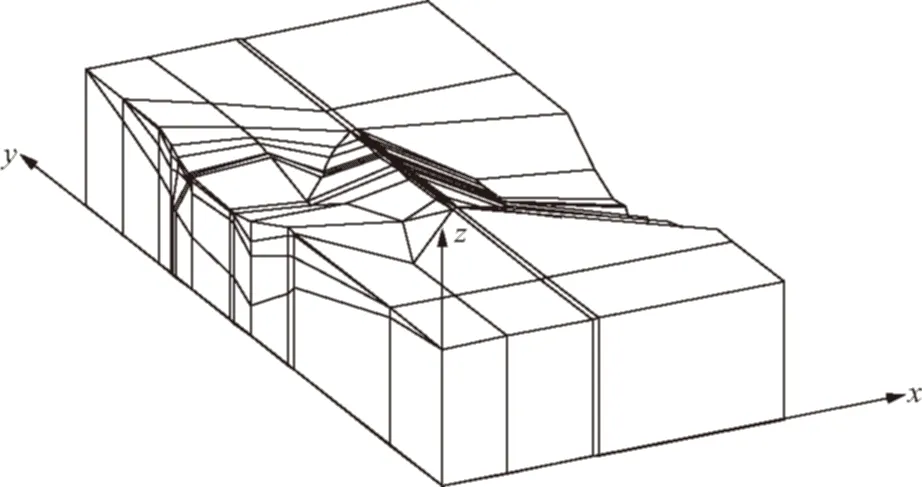
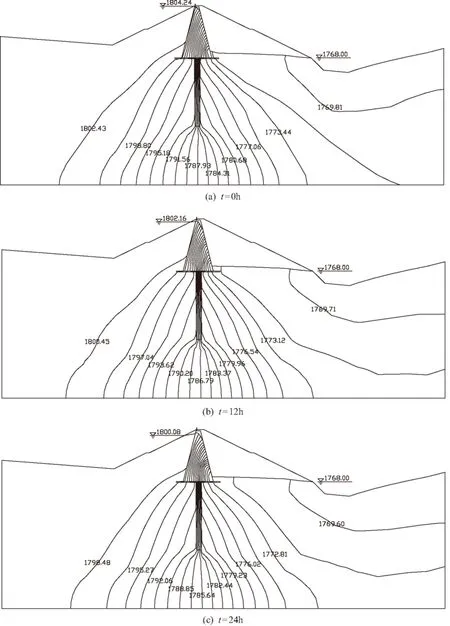
kr——相对透水率，为非饱和土渗透系数与饱和土渗透系数比值，在非饱和区0

β——饱和-非饱和选择常数，在非饱和区等于0，在饱和区等于1；

Ss——弹性贮水率，饱和土体的Ss为一个常数，在非饱和土体中Ss=0，当忽略土体骨架及水的压缩性时对于饱和区也有Ss=0；

Q——源汇项。

(2)

其中带“e”的符号表示相应于单元的量。

单元支配方程：

(3)

(4)

(5)

(6)

其中a、b=1～8， i、 j=1、3；

式中Na,Nb——单元形函数；

hc——压力水头。

将单元支配方程进行集成，可得整体有限元支配方程为：

(7)

(8)

2　工程概况

大黑箐水库位于宜良县竹山镇某村，属珠江流域南盘江左岸二级支流。水库主要功能是以农田灌溉供水及集镇、农村生活供水为主，兼顾保障下游防洪安全。水库总库容110.87万m3，工程规模为小(1)型，工程等别为Ⅳ等，主要建筑物级别为4级，临时建筑物级别为5级。水库设计洪水标准采用30年一遇，相应洪水位1803.76 m，校核洪水标准采用300年一遇，相应洪水位1805.18 m。溢洪道、输水洞消能防冲设计洪水标准采用20年一遇。临时建筑物设计洪水标准采用5年一遇。大坝采用黏土心墙坝，坝轴线长185m，坝顶高程1805.50m，坝顶设高1.2m混凝土防浪墙，墙顶高程1806.70 m，坝顶宽度为5m。

3　三维有限元模型

3.1计算模型范围

以大地坐标(513706.54，2729555.99)为模型坐标原点；该点位于右坝端0+000.00的坝轴线，取X轴为顺河流方向，垂直于坝轴线，上游指向下游为正；Y轴为坝轴线方向，右岸指向左岸为正；Z轴为垂直方向，向上为正，与高程一致。计算模型上游截取坝踵以上70.99m，边界至坝轴线上游约136.08m(X=0m)；下游截取坝趾以下82.00m，边界至坝轴线下游约168.13m(X=168.13m)；左岸截取坝肩山体205.73m，即边界至左坝端约205.73m(Y=395.14m)；右岸截取坝肩山体287.00m，即边界至右坝端约287.00m(Y=-287.00m)；底边界截取坝基帷幕最深处以下37.54m(一倍坝高)，至高程1680.00m；顶边界截至顶高程1840.30m，低于1840.30m的地形按实际高程考虑。该模型上下游方向宽度约304.21m，左右岸方向长度约672.14m，高度约160.30m。有限元网格结点总数为27141个，单元总数为25325个。三维超单元计算模型网格如图1所示。

图1　三维超单元计算模型网格

3.2模型边界条件

计算模型的边界类型主要有已知水头边界、出渗边界、不透水边界三种:ⓐ已知水头边界包括坝址区上、下游水位淹没线以下的给定水头边界，以及给定地下水位的截取边界；ⓑ出渗边界为坝区上、下游水位淹没线以上，左、右岸山坡的迎水面，为所有与大气接触的边界；ⓒ不透水边界包括模型底面以及模型上、下游截取边界。模型两侧截取边界根据计算的地下水位与原地下水位比较确定，可以是不透水边界，也可以给定地下水位边界。

4　计算参数选取

土坝水位骤升或骤降引起的非稳定渗流受较多因素影响，除上游水位上升或下降速度外，坝体材料渗透系数及坝体给水度等也很重要[6]。本文的给水度根据经验和文献资料参考类似工程选取，计算所需材料渗透参数如下表所列。

材料渗透参数表

5　计算成果分析

根据以上计算原理，采用三维非稳定饱和-非饱和渗流有限元计算程序，对水库在极端条件下(水位骤降4.16m/d)的非稳定渗流场进行了计算分析，计算得到的不同时刻典型断面等势线如图2所示。

图2　剖面Y=90m不同时刻位势分布

衡量库水位降落影响的指标一般采用比值K/(μv) (K为渗透系数，μ为介质的给水度，v为库水位下降速度)，该值反映了介质孔隙中水体降落速度与库水位降落速度间的关系，亦可以用于判别库水位降落速度对坝坡稳定性的影响，当K/(μv)<1/10时，自由面下降极缓；当K/(μv)>10时，孔隙水和库水位同步下降，随之泄尽，渗流对稳定性没有影响；当1/10

5.1坝壳渗流性态

从图2可以看出，上游坝壳内堆石区的自由面降落较快，与库水位的下降速度接近。由于坝壳料的渗透性较大，其渗透系数达1.00×10-2cm/s，相应的K/(μv)比值为20.83，比值较大，可认为上游坝壳内堆石区的自由面与库水位同步下降。在库水位降落的过程中，下游风化料坝壳内的自由面水位变化很小，坝壳内的渗透坡降也较小，不会对下游坝坡的稳定造成不利影响。

5.2心墙渗流性态

由于心墙的渗透系数很小，其渗透系数为6.28×10-6cm/s，相应的K/(μv)比值约为1.30×10-3，因此该水库库水位降落速度4.16m/d属于骤降。

从各时段末心墙的自由面位置变化来看，随着库水位不断下降，心墙内的自由面也随之下降，但降落速度较慢，远小于库水位的下降速度。从心墙内的自由面状态看，自由面最高点并不对称，偏向心墙上游侧。心墙内的自由面从最高点起向心墙两侧逐渐下降，在一定高度后出逸，沿心墙上游面和下游面向下，与坝壳内的自由面衔接。

在库水位降落起始时刻(t=0h)，心墙的最大渗透坡降为1.67。随着库水位降落，其值有所减小。当库水位降落到1800.08m时，心墙的最大渗透坡降减小1.31，小于心墙的允许渗透坡降。在库水位降落后，心墙内自由面高于上游坝壳，心墙上游侧渗透力的方向发生改变，由原来的指向下游转为指向心墙上游。

在库水位自校核洪水位1804.24m降落至正常蓄水位1800.08m时，心墙内的自由面最高点高出库水位约2.03m，约占初始时刻总水头的5.60%。在库水位降落后，心墙的最大渗透坡降有所降低，但是变化幅度不大。随着历时增加，心墙内饱和孔隙水逐渐排出，心墙内的自由面将逐渐降低，其渗透坡降亦将进一步减小。因此，不会对心墙的稳定造成不利影响。

6　结　论

a.在极端工况下(v=4.16m/d)，心墙上游坝壳浸润线几乎和水位同步下降，而由于心墙渗透系数较小，水主要滞留在心墙内，心墙内的自由面从最高点向心墙两侧逐渐下降，但心墙内的自由面最高点高出库水位不多，且心墙的最大渗透坡降小于允许坡降，因此满足渗透稳定性要求。

b.尽管在本文模拟分析工况下，心墙满足渗透稳定性要求，但由于浸润线高于库水位，势必存在一定的顺坡向渗流动水压力，而本文模拟工况，水位骤降历时较短，且水位降幅不大，从而忽略了这些因素的影响。

若考虑放空水库，由于水位降幅较大，则需要考虑这些因素的影响，合理地选择泄水速度，以免危及心墙坝坡的稳定。

[1]贾苍琴,黄茂松,王贵和,等.水位骤降对土坡稳定性的影响分析[J].同济大学学报(自然科学版),2008,(3):304-309.

[2]王学武,许尚杰,党发宁,等.水位骤降时的非饱和坝坡稳定分析[J].岩土力学,2010,(9):2760-2764.

[3]刘钊,柴军瑞,陈兴周,等.库水位骤降时坝体渗流场及坝坡稳定性分析[J].西安理工大学学报,2011,(4):466-470.

[4]王冬林,李宗利,张洪泉.库水位骤降对均质土坝坝坡稳定的影响分析[J].人民黄河,2011,(4):147-149.

[5]姜媛媛.饱和-非饱和渗流影响下非连续性岩体边坡稳定分析方法研究[D].南京:河海大学硕士学位论文,2005.

[6]顾慰慈.渗流计算原理及应用[M].北京:中国建材工业出版社,2000.

Analysis on the influence of reservoir water level sharp dropping on the clay core wall dam slope stability

WANG Zihuan1， ZHANG Xiaofeng2

(1.HenanWaterResourcesNo.2Bureau,Zhengzhou450016,China;2.GuotaiWaterSavingCo.,Ltd.,Beijing100053,China)

Dam slope stability is one important content in earth dam design. Pore water pressure cannot dissipate quickly in dam body under extreme conditions. Upstream dam slope has sliding trend due to higher pore water pressure and seepage force, and landslide accident can even be produced. On the basis, three-dimensional unsteady saturated-unsaturated seepage finite element method is applied for establishing 3D finite element model in Daheiqing Reservoir Area. The non-steady seepage field is simulated and analyzed aiming at the dam under extreme conditions. The results show that the reservoir water level is sharply dropped form the maximum flood water lever to normal water storage level within 1d, which cannot produce unbeneficial influence on the stability of core wall.

earth and rock-fill dam; core wall; unsteady seepage; finite element method; seepage slope

10.16616/j.cnki.11- 4446/TV.2016.09.011

TV641

A

1005-4774(2016)09- 0042- 04