模糊聚类方法在黄河流域重点断面水质分类中的应用
蒋红敬, 张振力, 郑喜英
(1.黄河科技学院,信息工程学院,河南 郑州 450063; 2.郑州航空工业管理学院 计算机学院,河南 郑州 450015)
模糊聚类方法在黄河流域重点断面水质分类中的应用
蒋红敬1, 张振力2, 郑喜英1
(1.黄河科技学院,信息工程学院,河南 郑州 450063; 2.郑州航空工业管理学院 计算机学院,河南 郑州 450015)
为评价黄河流域主要断面水质状况,选取4个统计指标,根据2016年第一季度水质状态样本数据,采用模糊聚类分析方法,对10个重点断面水污染状况进行模糊聚类,并对分类结果做了分析,分类结果符合实际情况.
水质分类;聚类分析;模糊聚类分析;等价关系;传递闭包
聚类分析的研究有几十年的历史,因其重要性及与其他学科的交叉应用而得到广泛关注,聚类分析是数理统计中的一种多元分析方法,它是按某种特定规律,依据事物的某些属性,将事物进行分类. 传统的聚类分析算法将每一个被划分对象严格归到某一类. 但现实中很多事物之间的界限不是明确的,并不具备严格的属性,可能介于一类或多类之间,如人的面貌相似程度分类、不同地区空气污染分类、天气预报的分类等.当涉及对带有模糊界限的事物进行聚类时,分类过程中要考虑事物之间的亲疏程度,用模糊数学的方法进行处理更为恰当,需运用模糊聚类分析方法. 模糊聚类分析方法给出的最终结果指明事物在某种程度上属于哪一类[1-2].
本文利用基于模糊等价关系的模糊聚类分析方法,考察黄河流域干流及支流10个观测点断面水质,选取pH值、溶解氧(Do)、高锰酸盐指数(CODMn)、氨氮(NH3-N)等4个统计指标对10个观测点水质状况进行聚类分析,结果表明,模糊聚类方法对水质的分类符合实际、科学合理,对有关部门掌握水质状况并采取相应措施有很大帮助,有广泛的实际应用价值.
1 样本数据
黄河流域干支流10个观测点分别为兰州新城桥、中卫新墩、石嘴山麻黄沟、乌海海勃湾、包头画匠营子、济源小浪底、济南泺口、海东民和桥、天水牛背、渭南潼关吊桥.观测点断面水质状况的好与差没有严格的评定界限,因此解决上述问题可以运用模糊聚类分析法.
以下对10个观测点水质污染状态相关程度分类.
为保证数据的稳定性,数据采用2016年第一季度黄河流域水质状况指标的周平均值,来源于中华人民共和国环境保护部政府网站数据中心. 设10个观测点组成一个分类集合
U=(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10).
每个观测点都采用pH值、溶解氧(Do)、高锰酸盐指数(CODMn)、氨氮(NH3-N) 4个统计指标表示水质状况,xi=(xi1,xi2,xi3,xi4)表示第i个观测点的水质状况,xij(i=1,2,…,10;j=1,2,3,4)表示第i个观测点第j个指标. 各观测点的统计指标值的原始数据见表1.
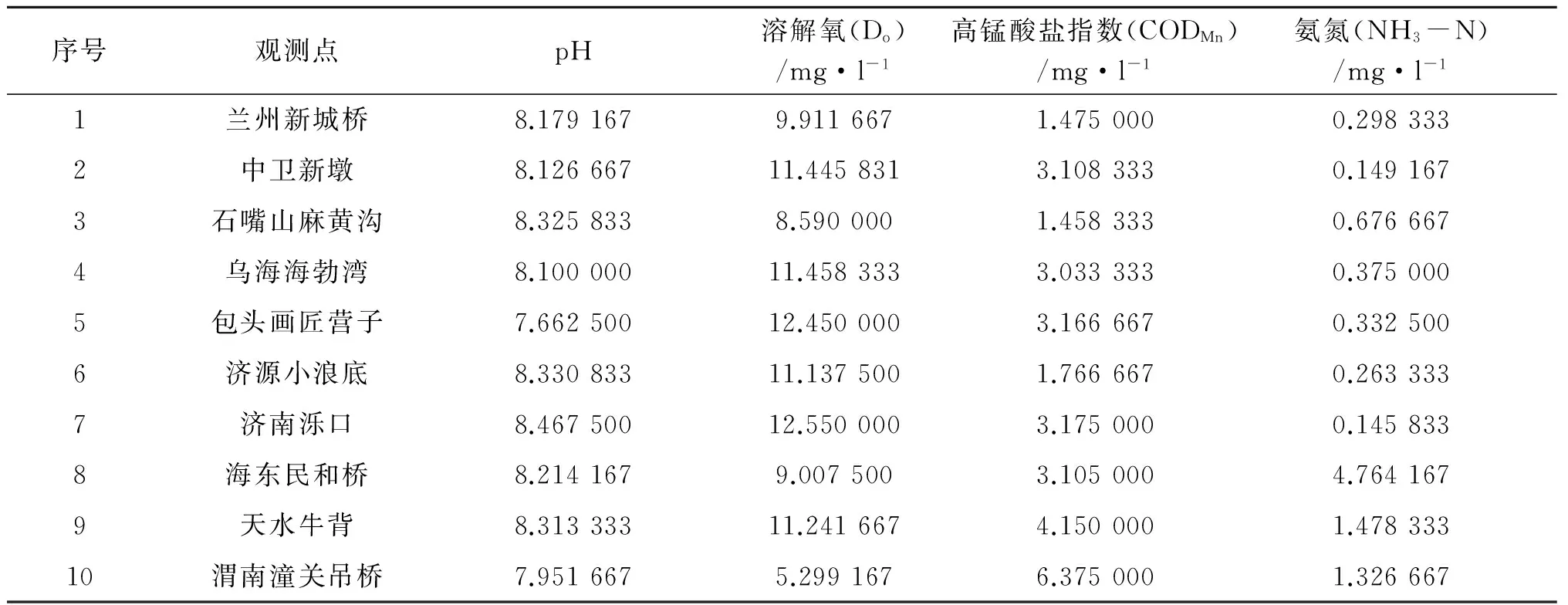
表1 黄河流域10个观测点水质指标的原始数据
2 数据标准化
4个统计指标量纲不同,需要将原始数据标准化,本文采用平移标准差-极差变换做归一化处理,两次处理后的结果分别为
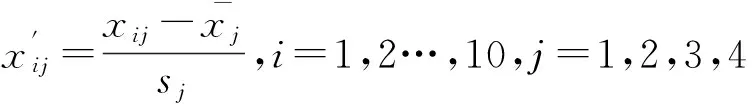
(1)
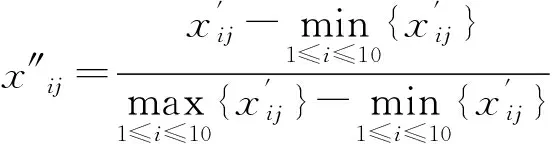
(2)
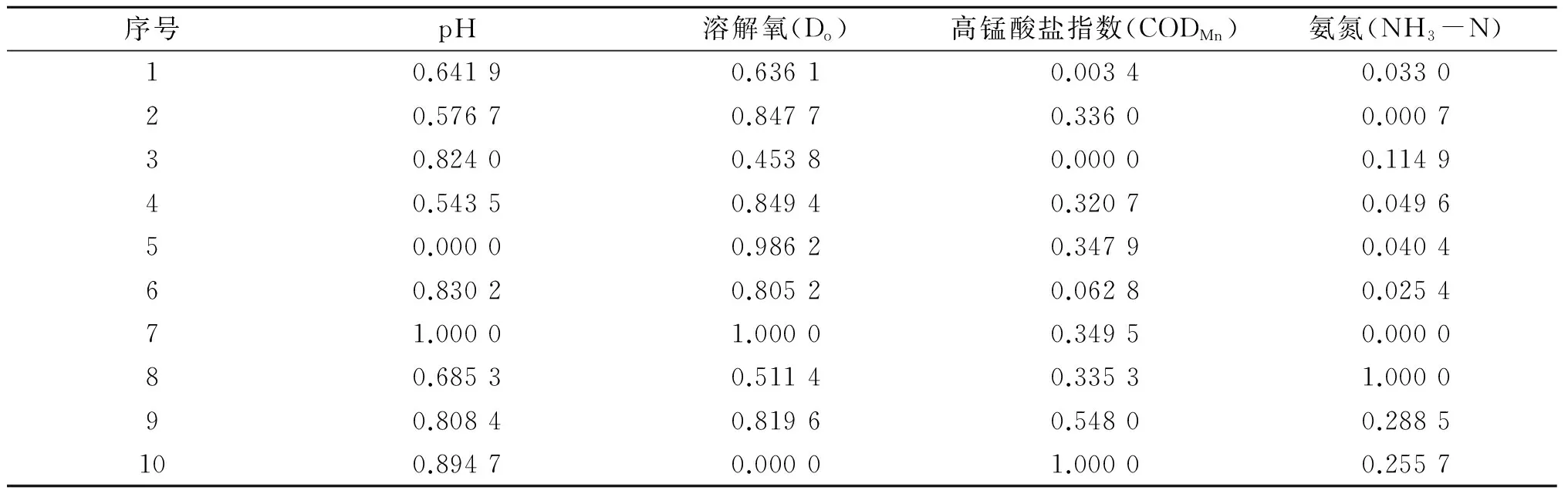
表2 黄河流域10个观测点断面水质状况的标准化数据
3 建立模糊相似矩阵
模糊相似矩阵的建立是模糊聚类分析的基础,本文采用最大最小法确定相似系数
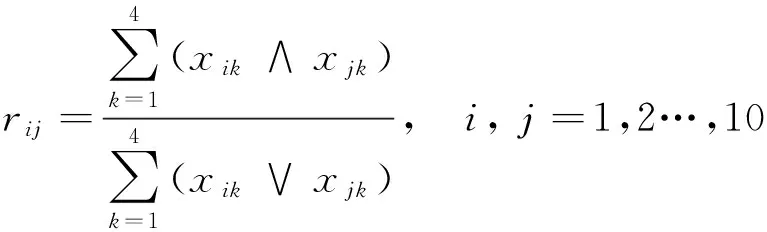
(3)
其中,rij∈[0,1]表示第i个观测点和第j个观测点在4个统计指标上的相似程度[4],将表2中的标准化数据代入公式(3)可求得各个观测点之间4个统计指标的模糊相似矩阵R.
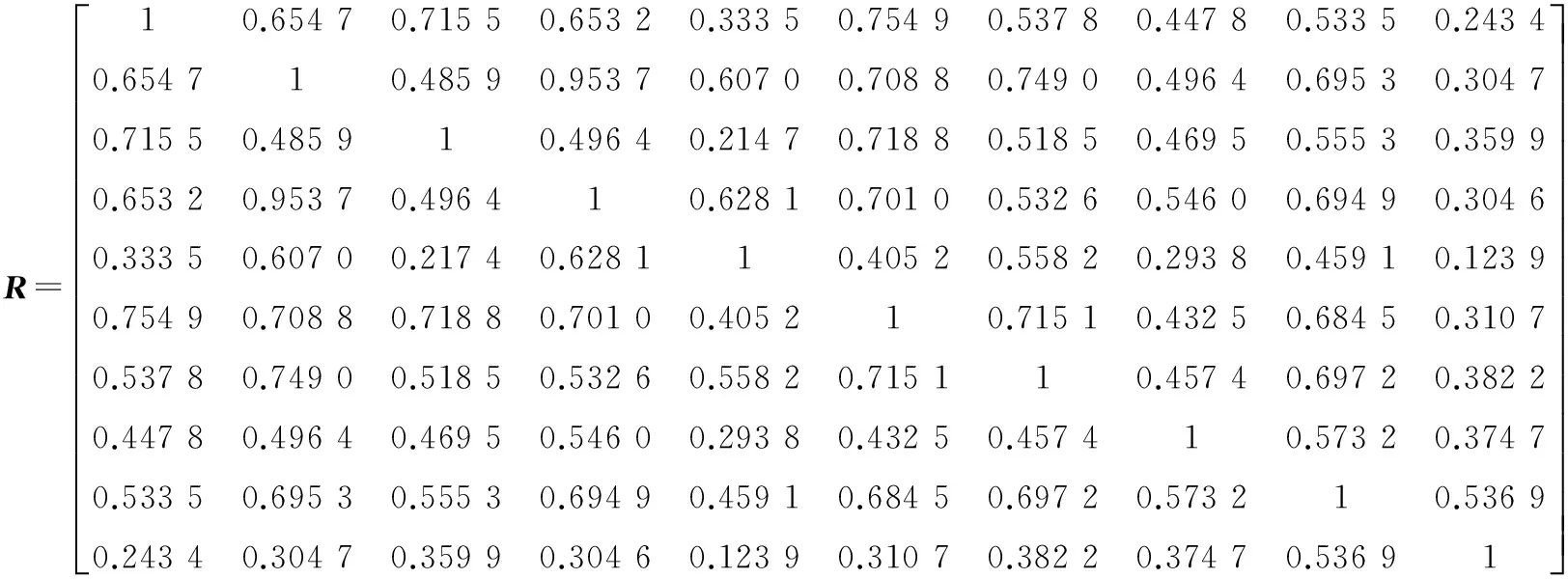
4 求取模糊等价矩阵
以上方法得到的模糊相似关系矩阵R具有自反性和对称性,但一般不满足传递性,而只有模糊等价关系才具有传递性,才有截运算[5]. 本文采用传递闭包法将模糊相似矩阵改造为等价矩阵,即利用相似矩阵的自身合成运算:R2=R∘R,R4=R2∘R2,…,直到出现R2k=Rk,则Rk是一个传递闭包,也即模糊等价矩阵t(R).经过计算,本文中k=4时,R8=R4,因此R4是模糊等价矩阵.
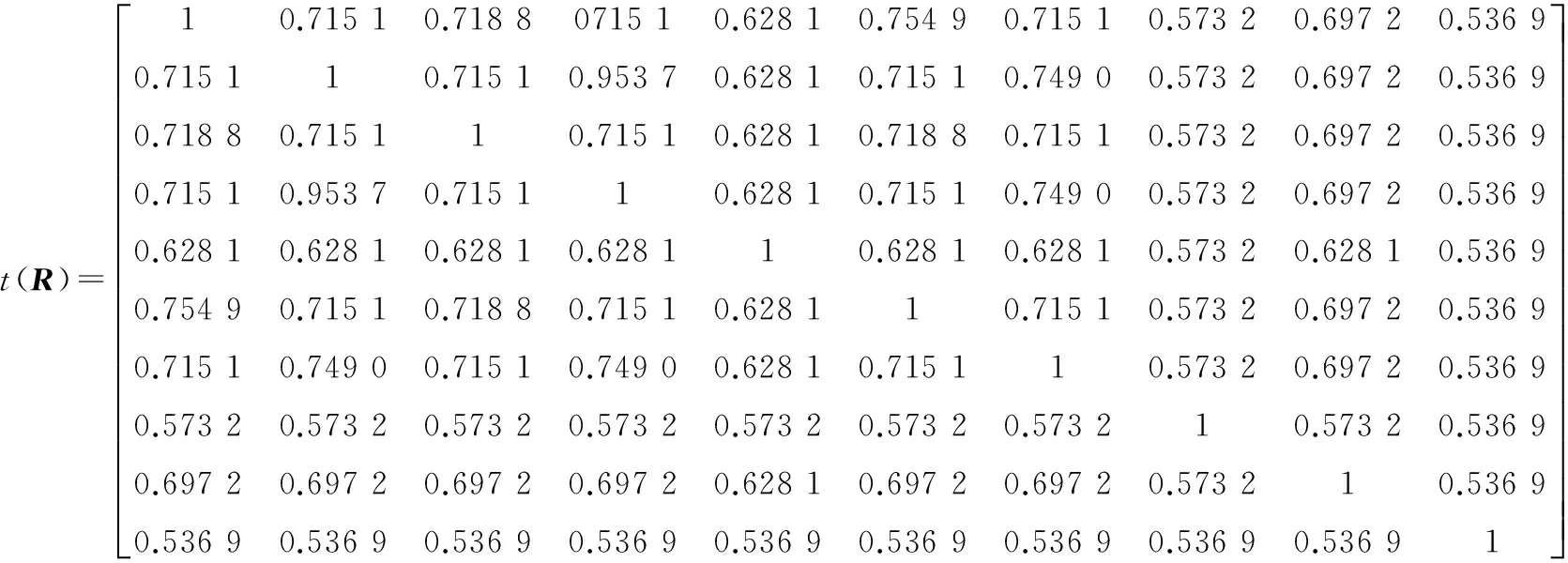
5 取不同阈值进行聚类分析
根据模糊等价矩阵,选取不同的阈值λ(0≤λ≤1),对应不同的截矩阵.当λ=0.697 2时,得到模糊等价矩阵的λ水平截矩阵如下

6 聚类结果分析与结论
从λ水平截矩阵可以看出,当λ=0.697 2时,黄河流域10个观测点水质状况可以分为4类.第一类{1,2,3,4,6,7,9}、第二类{5}、第三类{8}、第4类{10}.对应的观测点分类为{兰州新城桥,中卫新墩,石嘴山麻黄沟,乌海海勃湾,济源小浪底,济南泺口,天水牛背}、{包头画匠营子}、{海东民和桥}、{渭南潼关吊桥}.分类将水质特征不同的观测点区分开,特征相似的观测点归为一类.第一类观测点各指标受污染程度类似,海东民和桥的主要污染指标为氨氮,渭南潼关吊桥的主要污染指标为高锰酸盐指数,从而为黄河流域主要断面水污染治理和重点整治方向提供了依据,更便于因地制宜采取科学有效的措施.
近年来,模糊聚类分析方法广泛应用于工业、林业、农业、气象学等方面,聚类结果令人满意,本文利用模糊聚类分析方法对黄河流域重点断面水质进行分类,聚类结果合理,符合实际,进一步拓宽了该方法的应用领域.
[1]梁保松,曹殿立. 模糊数学及其应用[M]. 北京: 科学出版社, 2007:65-80.
[2]高新波. 模糊聚类分析及其应用[M]. 西安: 西安电子科技大学出版社, 2004:70-83.
[3]石艳,范兴华.长三角地区城市水安全模糊聚类分析[ J] .水电能源科学, 2014,32(4):147-150.
[4]董媛媛,黄琼.模糊聚类分析在高校学生成绩评价中的应用[J] .吉林省教育学院学报, 2015,31(3):46-47.
[5]梁承姬,嘉熲煚,徐德洪,等.两种模型在内陆无水港选址中的综合应用[J] .重庆交通大学学报(自然科学版), 2016,35(1):177-183.
Application of Fuzzy Cluster Method on Water Quality of Main Section of the Yellow River
JIANG Hongjing1, ZHANG Zhenli2, ZHENG Xiying1
(1.Institute of Information Engineering, Huanghe Science and Technology College, Zhengzhou 450063, China;2.DepartmentofComputerScience,ZhengzhouUniversityofAeronauticsManagement,Zhengzhou450015,China)
In order to evaluate the water quality situation in main section of the Yellow River, four statistical indicators are selected. Based on the sample data of water quality situation in the first quarter of 2016, water pollution situation of key sections is clustered by fuzzy clustering analysis method .The classification results which are identical with the actual situation are analyzed.
water quality classification; clustering method; fuzzy clustering analysis; equivalence relation; transitive closure law
2016-05-24
郑州市科技局基金项目(20141374);郑州航空工业管理学院教育科学研究基金项目(ZHJY16-42)
蒋红敬(1984—),女,山东聊城人,黄河科技学院信息工程学院讲师.
10.3969/j.issn.1007-0834.2016.03.004
O29; X824
A
1007-0834(2016)03-0010-04

