基于模型预测和谐振调节器的PMSM电流控制

刘旭东，张承慧，顾欣，李珂

（山东大学控制科学与工程学院，山东 济南 250061）

基于模型预测和谐振调节器的PMSM电流控制

刘旭东，张承慧，顾欣，李珂

（山东大学控制科学与工程学院，山东 济南 250061）

为了提高永磁同步电机（PMSM）的控制性能，提出了一种基于模型预测控制（MPC）和谐振调节器的电流控制方法。首先，通过建立预测模型和滚动优化，设计PMSM电流预测控制器。然后，针对电流谐波造成的电机转矩脉动问题，在模型预测电流控制方法基础上引入了谐振调节器。实验结果表明，所提方法具有良好的电流动态性能和电流跟踪特性，且能有效地改善电流波形，减小转矩脉动。

永磁同步电机；模型预测；谐振调节器

永磁同步电机（PMSM）具有效率高，功率密度大，可靠性强等优势，在电动汽车，机器人，航空航天等领域受到越来越多的关注。然而，永磁同步电机是一个多变量，强耦合的复杂非线性系统，且存在外部扰动和不确定性，要实现电机的高性能控制，必须克服这些因素对电机的影响。

模型预测控制（MPC）作为一种新型的控制方法，该方法利用系统的输入输出，建立预测模型，通过优化成本函数，得到控制律，因具有控制效果好，对模型精确性要求不高，鲁棒性强等特点，备受关注［1］，近年来已在PMSM电流控制［2-4］中得到广泛应用。

尽管模型预测电流控制具有较好的电流响应动态性能，对系统参数变化和外部扰动具有较强的鲁棒性，但是预测控制仍不能消除周期性的扰动。在矢量控制中，当电流测量不准确时，通过坐标变换得到的dq轴电流会存在谐波，不能完全控制为直流，进而造成电流波动和转矩脉动，这在高性能的电机控制场合是不允许存在的。因此在控制器的设计中，需要考虑电流测量误差的影响，抑制转矩脉动。目前，在PMSM控制中电流谐波抑制方法主要包括设计干扰观测器［5］，重复控制［6］以及谐振调节器方法［7-8］。其中，谐振控制是根据内模原理推导而来，具有在谐振频率处增益接近无穷大，可有效抑制谐振频率处谐波，获得良好的稳态性能。

为此，本文结合模型预测控制方法和谐振调节器，设计了永磁同步电机的电流跟踪控制器，使得电机不仅具有良好的动态性能，而且能有效地减小电流波动，抑制转矩脉动，提高稳态性能。最后搭建了基于dSPACE的永磁同步电机双闭环试验平台，通过实验验证了该方法的有效性。

1　永磁同步电机模型

按转子磁场定向理论，PMSM在d-q同步旋转坐标系下的数学模型可表示为

式中：Ld，Lq为d-q同步旋转坐标系下的定子电感；id，iq，ud，uq分别为d-q坐标系下的定子电流和电压；Rs为定子电阻；np为极对数；ω为转子机械角速度；Ψ为永磁体产生的磁链；J为转动惯量；τL为负载转矩；B为摩擦系数；fd，fq为由参数变化引起的扰动量。

定义如下：

其中

式中：Rst,Ldt,Lqt,Ψt为实际的参数值。

本文采用标准级联的PMSM矢量控制方法，外环为转速环，内环为电流环。转速环采用PI控制，本文主要研究电流环的控制问题，将采用模型预测控制方法和谐振调节器的复合控制策略，实现电流的快速跟踪控制，并抑制电流波动。控制系统的结构框图如图1所示。

图1　PMSM控制系统结构框图Fig.1　Block diagram of PMSM control system

2　电流预测控制器设计

电流预测控制器的目标是实现电流环快速跟踪控制，首先对于PMSM模型，不考虑扰动项，由式（1）得：

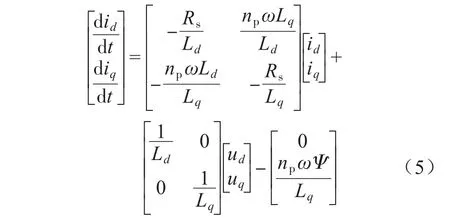
取采样时间为Ts，由式（5）可得离散化后的PMSM模型可表示为

由此可得：

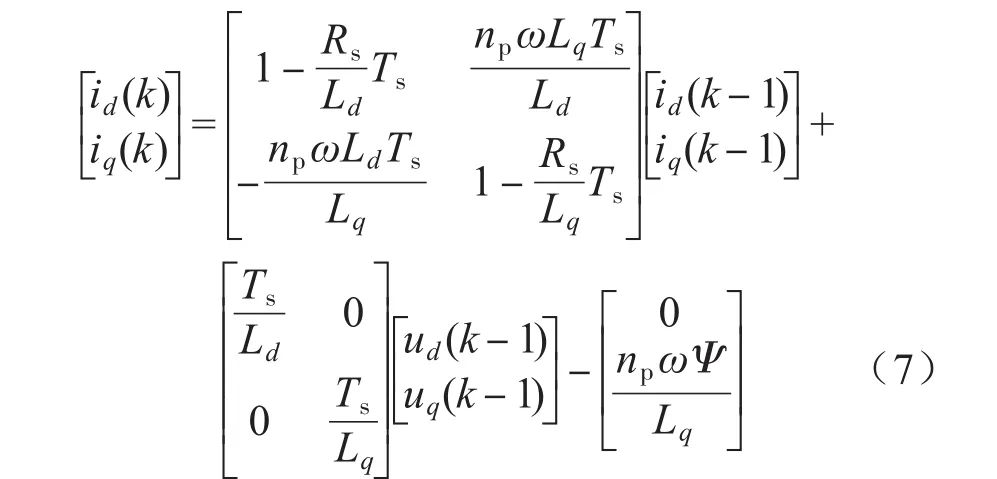
由式（6）和式（7）得：

其中

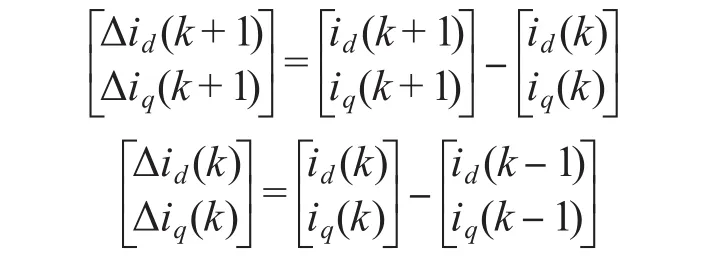
定义状态量

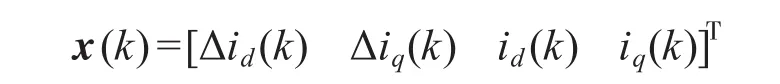
输入量

输出

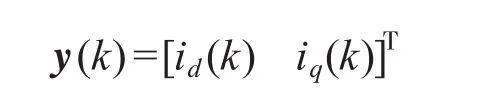
可得

其中

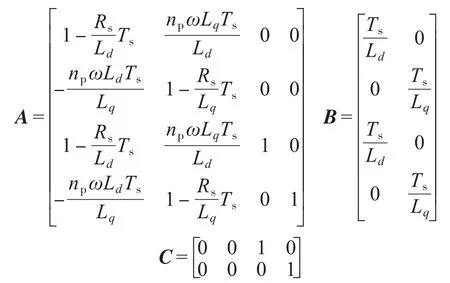
令预测时域和控制时域分别为Np和Nc，并且在采样时刻k，当i＞Nc-1，u（k+i）保持不变，i=0,1,…,Np-1，本文取Nc=1，可得：

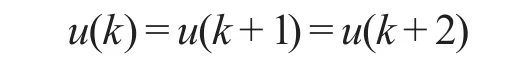
因此

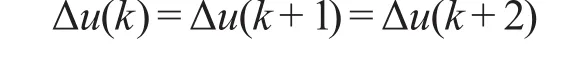
预测的状态量x（k+i+1）为

基于预测状态变量式（11），预测输出量y（k+i+1）可写为

令

则

令 r（k）=［i*d（k）i*q（k）］为参考电流，根据文献［1］的模型预测控制求解方法可得：

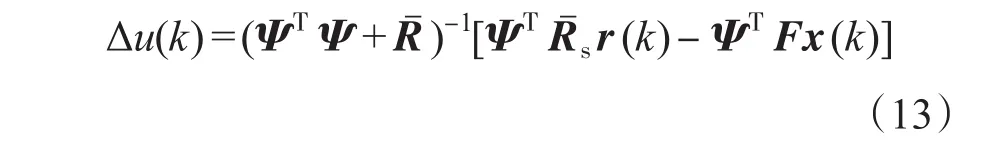
式中：Rˉ为权重矩阵；ΨTRˉs为ΨTF的后两列组成的矩阵。

进而由式（9）可求得u（k），即ud（k），uq（k）。

3　谐振调节器设计

虽然电流预测控制器使电机具有良好的动态响应性能和鲁棒性，但不能消除周期性的扰动。在实际工况中，由于电流测量误差的存在，容易导致电流存在大量谐波，进而引起电流波动和转矩脉动。电流测量误差主要包括电流偏置误差和电流增益误差。

3.1电流偏置误差

电流偏置误差是测量的正弦相电流含有直流分量，可表示为

式中：ia，ib为电机实际的相电流；

为通过电流传感器测得的含有直流分量的相电流。

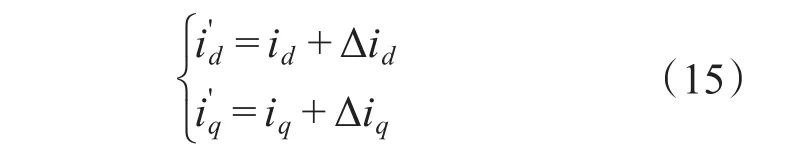
通过坐标变换后，测得的dq轴电流为其中，Δid，Δiq为相电流的直流分量带来的dq轴电流扰动，可以表示为［9］式中：θ为电机转子电角度。

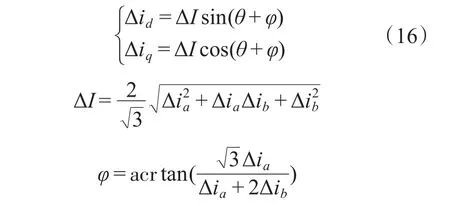
由式（16）看出，Δid，Δiq的频率等于电机的电角频率。

3.2电流增益误差

电流增益误差指测得的相电流为

其中，ka＞0，kb＞0为电流增益。假设经坐标变换后，由于电流增益误差，测得的dq轴电流表示为

求得［9］：

由式（19）看出，Δid1，Δiq1的频率等于电机电角频率的2倍。

3.3谐振调节器

由上可知，在dq轴坐标系下，dq轴电流谐波主要包括1次和2次谐波。为了抑制电流谐波造成的影响，本文引入了谐振调节器的控制方法［7］，谐振调节器的传递函数如下：

式中：ω1为谐振频率；k为比例系数。

谐振调节器在谐振频率处增益接近无穷大，可有效抑制谐振频率处谐波，其结构框图如图2所示。

图2　谐振调节器结构框图Fig.2　Block diagram of resonant controller

由于谐波频率随电机转速的变化而变化，为了抑制电流的1，2次谐波，分别取 ω1=ωe, ω1=2ωe,ωe为电机的电角速度。

通过在模型预测电流控制器基础上分别并联谐振调节器，可有效抑制由电流测量误差引起的电流波动，提高电机的稳态性能。

4　实验验证

为了验证所提方法的电机控制性能，利用dSPACE公司的MicroAutobox作为电机控制器，通过搭建快速控制原型，完成了实验验证。系统包括永磁同步电机、dSPACE控制器、功率变换器、测功机以及控制器，电机参数为：额定转速3 000 r/min,额定转矩2.3 N·m,定子电阻4.8 Ω,d轴电感19.5 mH,q轴电感27.5 mH。在控制器中，采用双闭环的矢量控制结构，转速环采用PI控制，电流环采用本文方法。为了验证该方法的有效性，将含有谐振调节器的模型预测电流控制与不含谐振调节器的电流控制方法对比。

在模型预测电流控制器，取采样时间Ts= 0.001 s，预测时域Np=5。给定电机转速600 r/min，负载转矩0.5 N·m。图3为不含有谐振调节器时的dq轴电流和电磁转矩响应曲线。从图3中看出，设计的模型预测电流控制器具有良好的电流跟踪性能，但当电机稳定之后，dq轴电流波动仍较大，造成的电机输出转矩波动大，稳态性能较差。

图3　无谐振调节器时的模型预测电流控制Fig.3　Model predictive current control without resonant controller

给定相同的转速和负载条件，采用基于模型预测控制和谐振调节器的复合控制方法，取谐振系数k=0.5，图4为对应的dq电流和电磁转矩曲线。从图4看出，该方法不仅具有较好的电流跟踪特性，而且在电机稳定后，电流和转矩波动更小，稳态性能更好。

图4　含有谐振调节器时的模型预测电流控制Fig.4　Model predictive current control with resonant controller

为了验证本文所提方法在控制器和电机参数不一致条件下的电流控制性能，将控制器中的电感参数变为电机实际参数的0.5倍，给定电机转速为600 r/min，负载转矩0.5 N·m，图5为对应的dq轴电流曲线。从图5中看出，虽然电感参数变化，但dq轴输出电流能快速地跟踪给定值，具有良好的电流跟踪性能，对参数的变化具有较强的鲁棒性。

图5　参数变化下的电流控制性能Fig.5　Current control performance when the parameters change

5　结论

本文提出了一种新型的永磁同步电机电流控制方法。首先基于模型预测控制理论，设计了电流预测跟踪控制器，该方法具有良好的动态响应性能；进而针对电流中的谐波引起的电流波动问题，设计了谐振调节器，有效地减小了电流波动，抑制了转矩脉动，提高了电流控制的稳态性能。最后通过实验证明了该方法不仅具有良好的动静态性能，而且具有较强的鲁棒性。

［1］Wang L P.Model Predictive Control System Design and Implementation Using MATLAB［M］.London，Springer Verlag，2009.

［2］Morel F，Lin-Shi X F，Retif J M.A Comparative Study of Predictive Current Control Schemes for a Permanent-magnet Synchronous Machine Drive［J］.IEEE Trans.on Industrial Electronics，2009，56（7）：2715-2728.

［3］Chai S，Wang L P，Rogers E.A Cascade MPC Control Structure for a PMSM with Speed Ripple Minimization［J］.IEEE Trans.on Industrial Electronics，2013，60（8）：2978-2987.

［4］Bolognani S，Bolognani S，Peretti L.Design and Implementation of Model Predictive Control for Electrical Motor Drives ［J］.IEEE Trans.on Industrial Electronics，2009，56（6）：1925-1936.

［5］Yamaguchi T，Tadano Y，Hoshi N.Compensation of the Current Measurement Error with Periodic Disturbance Observer for Motor Drive［C］//the International Power Electronics Conference，2014：1242-1246.

［6］Mattacelli P，Tubiana L，Zigliotto M.Torque-ripple Reduction in PM Synchronous Motor Drives Using Repetitive Current Contro［lJ］.IEEE Trans.on Power Electronics，2005，20（6）：1423-1431.

［7］李毅拓，陆海峰，瞿文龙，等.基于谐振调节器的永磁同步电机电流谐波抑制方法［J］.中国电机工程学报，2014，34 （3）：423-430.

［8］王贺超，夏长亮，阎彦，等.基于谐振控制的表贴式永磁同步电机弱磁区电流谐波抑制［J］.电工技术学报，2014，29 （9）：83-91.

［9］Qian W，Panda S，Xu J X.Torque Ripple Minimization in PM Synchronous Motors Using Iterative Learning Control［J］. IEEE Transactions on Power Electronics，2004，19（2）：272-279.

Current Control Based on Model Predictive and Resonant Controller for PMSM

LIU Xudong，ZHANG Chenghui，GU Xin，LI Ke
（School of Control Science and Engineering，Shandong University，Jinan 250061，Shandong，China）

A current control method based on model predictive control and resonant controller was proposed to improve the control performance of permanent magnet synchronous motor（PMSM）.Firstly，the current predictive controller for PMSM was designed through predictive model and rolling optimization.Then，for the torque-ripple caused by the current harmonic，the resonant controller was introduced to the predictive controller.The experimental results showed that，the proposed method has good dynamic performance and current tracking performance.It can also improve current waveform and reduce the torque-ripple effectively.

permanent magnet synchronous moto（rPMSM）；model predictive；resonant controller

TM341

A

2015-09-15

国家重点基础研究发展计划（973计划）（2013CB035600）；国家自然科学基金重大国际（地区）合作研究项目（61320106011）；国家自然科学基金资助项目（51277116；61304033；61304029；61403236）

刘旭东（1987-），男，博士研究生，Email：xudong19871982@163.com