深吃水半潜式平台参数共振研究

毛 欢，杨和振

(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240)

深吃水半潜式平台参数共振研究

毛 欢，杨和振

(上海交通大学 船舶海洋与建筑工程学院 海洋工程国家重点实验室，上海 200240)

深吃水半潜式平台(deep draft semi-submersible,DDS)作为一种新型海洋结构物，既继承了传统半潜式平台的优点，又改善了传统半潜式平台垂荡运动性能差的不足。但随着吃水的增加，DDS纵摇运动参数共振也成为一个不容忽视的问题。当DDS纵摇运动固有周期和垂荡运动周期满足一定关系时，纵摇运动将发生参数共振,纵摇角度将会显著增大。研究推导了DDS纵摇运动方程，并简化为标准的马修方程，运用希尔无穷行列式法求解马修方程，得到了含阻尼的马修稳定性图谱，并结合具体算例讨论了不同参数对DDS纵摇运动参数共振问题的影响。研究表明：深吃水半潜式平台的参数共振，是设计人员在设计之初必须考虑的问题；通过合理选取平台的系统参数，可以有效避免纵摇运动参数共振现象的发生。

深吃水半潜式平台；参数共振；马修方程 ；动力响应

Abstract:Parametric resonance of a Deep Draft Semi-submersible(DDS) platform is studied.As a new offshore structure,DDS not only inherits the advantages of traditional semi-submersible platform,but also improves its heave performance.But with the draft increasing,parametric resonance of DDS pitch motion cannot be ignored.When DDS pitch motion natural period and heave motion period satisfy a certain relationship,parametric resonance of pitch motion will occur,and the pitch angle will increase significantly.For the present problem,the pitch motion governing equation of DDS is established,then the equation is simplified to Mathieu equation.Mathieu equation is solved by the method of Hill infinite determinant,then Mathieu stability diagram with damping is obtained.Based on specific examples,the effect of different parameters on the DDS pitch motion parametric resonance is studied.The result shows that parametric resonance of a DDS platform must be taken into consideration in its conceptual design stage; meanwhile,parametric resonance can be effectively avoided by choosing the reasonable parameters of DDS.

Keywords:deep draft semi-submersible; parametric resonance; Mathieu equation; dynamic response

半潜式海洋平台自20世纪60年代初出现以来，得到了很大地发展和应用。半潜式海洋平台具有生产成本相对较低、甲板空间和甲板可变载荷大、水动力性能优良和工作水深范围大等优点。但是，半潜式平台垂荡运动较大，干采油树系统不能应用在其上，在一定程度上制约了半潜式平台的进一步发展[1]。近年来，为改善半潜式平台的垂向运动性能，国际上提出了深吃水半潜式平台(deep draft semi-submersible,DDS)概念[2]，如图1所示。但是由于平台吃水的增加，也带来一个新的问题，即深吃水半潜式平台的参数共振问题。

参数共振问题在数学上是由于运动控制方程的参数发生周期性变化，导致方程的时域解发散；在海洋工程领域，是由于系统的参数发生周期性变化，导致海洋结构物某些自由度的运动出现不稳定性现象。目前多种海洋结构物(船舶，顶张力立管TTR，张力腿平台和Spar平台等)，在实际应用或实验中都曾发生了参数不稳定性现象。

1998年APL CHINA号集装箱船在北太平洋海域遭遇强烈风暴，船舶发生大角度横摇，导致大部分集装箱丢失和损坏。事后研究发现：船舶发生大角度横摇运动是由于船舶在迎浪情况下发生了参数横摇[3]。此后多名学者都对船舶参数横摇进行了研究。Spyrou[4]、Neves等[5]、Lu等[6]分别研究了船舶在随浪、迎浪和不规则波中的参数横摇。

1998年Huse等[7]在空旷海域进行了钢制顶张力立管(TTR)模型试验，结果发现，TTR存在大幅的轴向张力波动。此后学者们相继对TTR的参量共振问题进行了研究。在杨和振等[8]研究了参数激励下深海立管的不稳定性问题之后，肖飞等[9]接着研究了TTR在双频激励下的参量不稳定性问题，随后，Yang等[10]研究了TTR在漩涡脱落和多频参数激励联合作用下的不稳定现象。

图1 深吃水半潜式平台Fig.1 Deep Draft Semi-submersible(DDS)

学者们对Spar平台参数不稳定性问题的研究也由来已久，在Haslum[11]使用简化的计算方法研究了Spar平台的参数不稳定性问题，并给出不含阻尼的马修稳定性图谱之后，Rho等[12]和Koo等[13]接着分别研究了阻尼板、系泊设备和立管对Spar平台纵摇稳定性的影响。

2012年王俊荣等[14]对传统半潜式平台的Mathieu不稳定性问题进行了研究。深吃水半潜式平台(DDS)作为一种新型深水浮式平台，目前鲜有学者研究过其参数共振问题。本文针对DDS这一新型海洋结构物，研究了其在规则波中的参数不稳定性问题，建立其理论模型，推导了纵摇运动的马修方程，运用希尔无穷行列式法求解不稳定区域，并结合具体算例讨论了不同参数对DDS参数共振问题的影响。

1 基本理论

1.1深吃水半潜式平台纵摇运动方程

深吃水半潜式平台的垂荡和纵摇运动是相互的耦合运动，垂荡运动会引起平台纵稳性高的变化，纵摇回复力矩会受到垂荡运动的影响，如图2所示。

考虑线性阻尼的影响，平台的纵摇运动方程可以表示为：

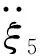
式中：I55为平台纵摇转动惯量；A55为纵摇附加转动惯量；C55为平台纵摇阻尼系数；ρ为海水密度；new为时变的排水体积；为时变的纵稳性高度；ξ5(t)为纵摇角度；Fω5为波浪激励力矩幅值；ω5为纵摇固有频率。

图2 DDS垂荡-纵摇耦合示意Fig.2 Schematic of heave and pitch of DDS

由于平台水线面惯性矩相对排水体积来说，是一个小量，因此稳心半径亦是一个小量，故可以忽略由于垂荡运动而引起的稳心半径的变化，瞬时纵稳性高度可以表示为：

式中：ξ3(t)为垂荡位移；η为波面升高。

为了简化，引入以下两个假设：

1)平台垂荡运动为一阶简谐运动，忽略波浪升高项的影响，垂荡运动可以表示为:

式中：ξ3,ω3分别为垂荡运动幅值和频率。

2)在垂荡共振条件下，垂荡运动能量会向纵摇运动转移，纵摇波浪激励力矩对纵摇运动影响不大，因此忽略纵摇波浪激励力矩的作用。

将式(2)和式(3)代入式(1)可得：

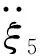
令τ=ω3t，则式(4)可以简化为标准的马修方程：

式中：

1.2希尔无穷行列式法求解马修方程

运用希尔无穷行列式法求解马修方程，边界曲线的解用傅里叶级数表示。根据Floquet理论，具有周期系数的线性微分方程的边界曲线能把α-β平面分成稳定区域和不稳定区域。沿着边界曲线方程(5)至少有一个解是周期性的，将方程以2π为周期的周期解定义为：

对于任意时间τ，式(7)均成立的必要条件是所有的系数为零：

有关{sn}的无限方程组要有非零解，则其无穷系数行列式必须为零，假设α+inc-n2≠0，则：

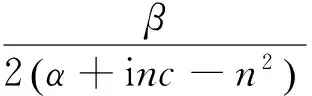
解无穷行列式(9)，取行列式维数为100×100，并取不同的临界阻尼系数，可得图3所示的马修稳定性图谱。当深吃水半潜式平台的参数落入稳定区时，不会发生参数共振；反之，若参数落入不稳定区则会发生参数共振。

深吃水半潜式平台可能发生纵摇参数共振的不稳定区主要集中在第一不稳定区和第二不稳定区。从图3中可以看出，随着阻尼增大，不稳定区的范围变小，第二不稳定区受阻尼的影响更加显著。当α=0.25，即纵摇固有频率是垂荡频率的一半时，不稳定区范围最大，因此设计时应尽量使平台的纵摇固有频率远离垂荡频率的一半。

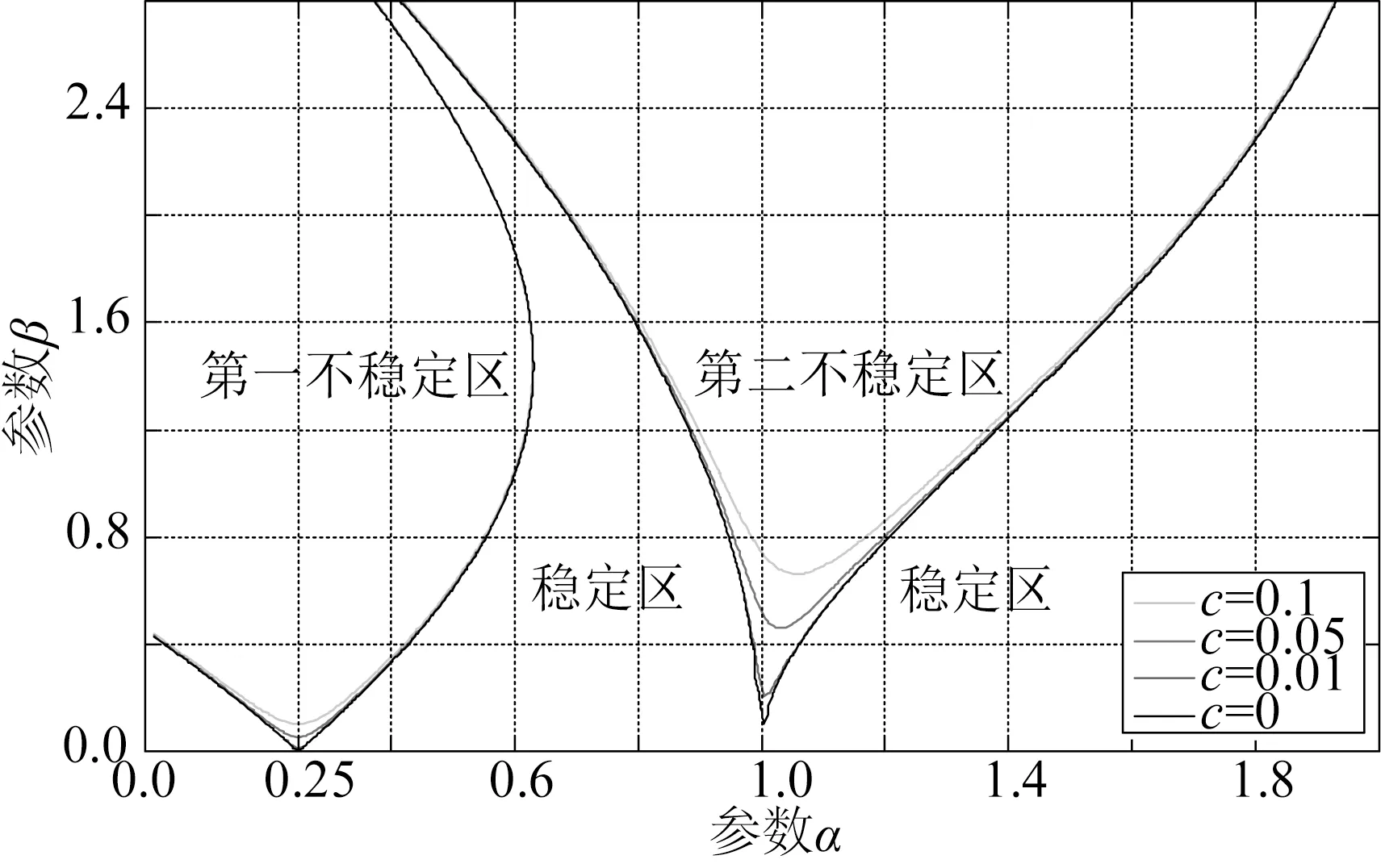
图3 有阻尼的马修稳定性图谱Fig.3 Stability diagram for damped Mathieu's equation

图4 某深吃水半潜式平台示意Fig.4 Schematic diagram of a Deep Draft Semi-submersible platform

2 算例分析

以某石油公司提出的深吃水半潜式平台为例，进行参数稳定性分析。平台示意如图4所示，平台主要参数如表1所示。

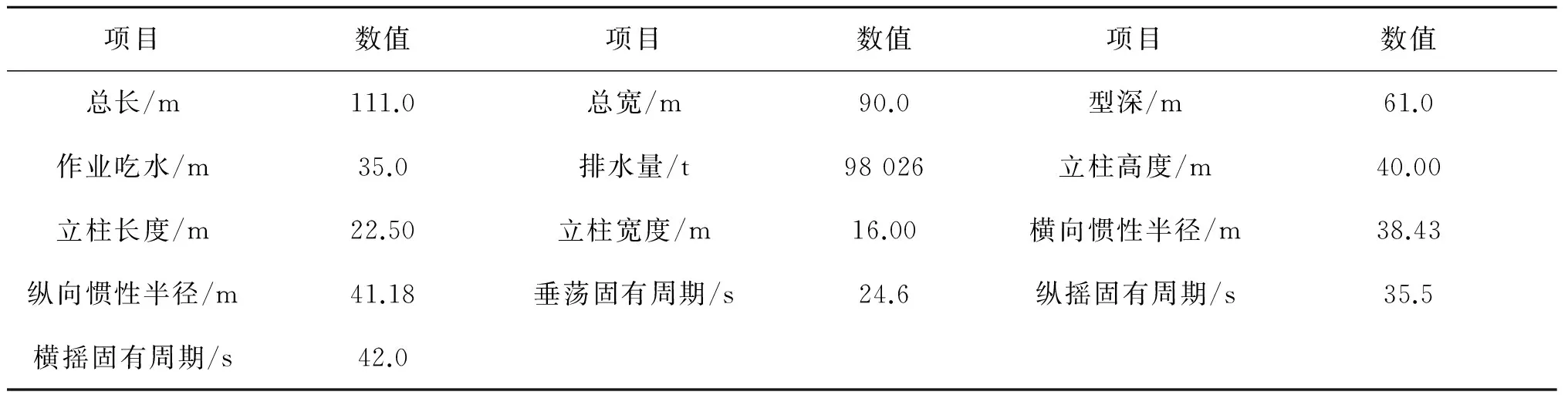
表1 深吃水半潜式平台主要参数Tab.1 Main parameters of the DDS

深吃水半潜式平台的纵摇稳定性与垂荡周期/纵摇固有周期比、垂荡运动的幅值和纵摇阻尼大小密切相关，下面将逐一讨论。

2.1垂荡周期/纵摇固有周期比的影响

表2给出了分析垂荡周期/纵摇固有周期比对平台纵摇稳定性影响的4种工况(表中ξ3为垂荡幅值，T为波浪周期，T5为纵摇固有周期，c为纵摇阻尼)。在规则波中，平台垂荡运动周期等于波浪周期，因此工况A1～A3通过改变波浪周期、工况A4通过改变纵摇固有周期，来改变垂荡周期/纵摇固有周期比，垂荡幅值统一取为2.5 m，纵摇阻尼比取为3%。

表2 工况A1～A4参数Tab.2 Parameters of Cases A1～A4

工况A1情况下，垂荡周期与纵摇固有周期比接近1∶2，假设平台纵摇初始扰动位移为(π/180) rad，初始加速度为0。平台纵摇运动响应情况如图5(a)所示，在200 s之后，纵摇运动幅值开始逐渐增大，纵摇运动出现不稳定性现象。

工况A2和A3情况下，分别减小和增大了波浪周期，从而使垂荡周期/纵摇固有周期比远离1∶2，平台纵摇运动幅值逐渐减小，纵摇运动处于收敛状态，如图5(b)和5(c)所示。

工况A4情况下，将平台的稳性高由2.66 m增加到3.37 m，平台纵摇固有周期由35.5 s减小为31.5 s，其他参数不变，平台纵摇运动响应情况如图5(d)所示。纵摇运动幅值逐渐减小，处于收敛状态。由此可见，改变平台纵摇运动固有周期，使其远离波浪周期的2倍，使马修方程的参数偏离不稳定区域，可以有效避免纵摇运动参数共振现象的发生。

图5 工况A1～A4纵摇运动时程Fig.5 Pitch motion history of Cases A1～A4

2.2垂荡运动幅值的影响

表3给出了分析平台垂荡运动幅值影响的2种工况，纵摇阻尼比统一取为3%，波浪周期为17.5 s，垂荡运动周期与纵摇运动固有周期比接近1∶2。

在工况B1情况下，垂荡运动幅值ξ3=2.0 m，平台纵摇运动响应情况如图6(a)所示。可以看出平台纵摇运动幅值逐渐增大，纵摇运动处于不稳定状态。

在工况B2情况下，减小了平台垂荡运动幅值，平台纵摇运动响应情况如图6(b)所示。平台纵摇运动幅值逐渐减小，纵摇运动处于收敛状态。可见，减小平台垂荡运动幅值能够有效抑制纵摇运动参数共振现象的发生。

表3 工况B1、B2参数Tab.3 Parameters of Cases B1 and B2

2.3纵摇阻尼的影响

表4给出了分析平台纵摇阻尼影响的2种工况，垂荡运动幅值统一取为2.5 m，波浪周期为17.5 s。

工况C1情况下，纵摇阻尼为5%，平台纵摇运动响应情况如图7(a)所示，平台纵摇运动逐渐发散，纵摇运动处于不稳定状态。

工况C2情况下，将纵摇阻尼增大为8%，平台纵摇运动幅值逐渐减小，纵摇运动收敛，如图7(b)所示。可见，增大平台纵摇阻尼可以有效避免纵摇运动参数共振现象的发生。

表4 工况C1、C2参数Tab.4 Parameters of Cases C1 and C2

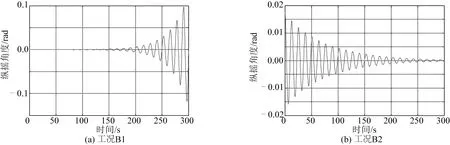
图6 工况B1、B2纵摇运动时程Fig.6 Pitch motion history of Cases B1 and B2

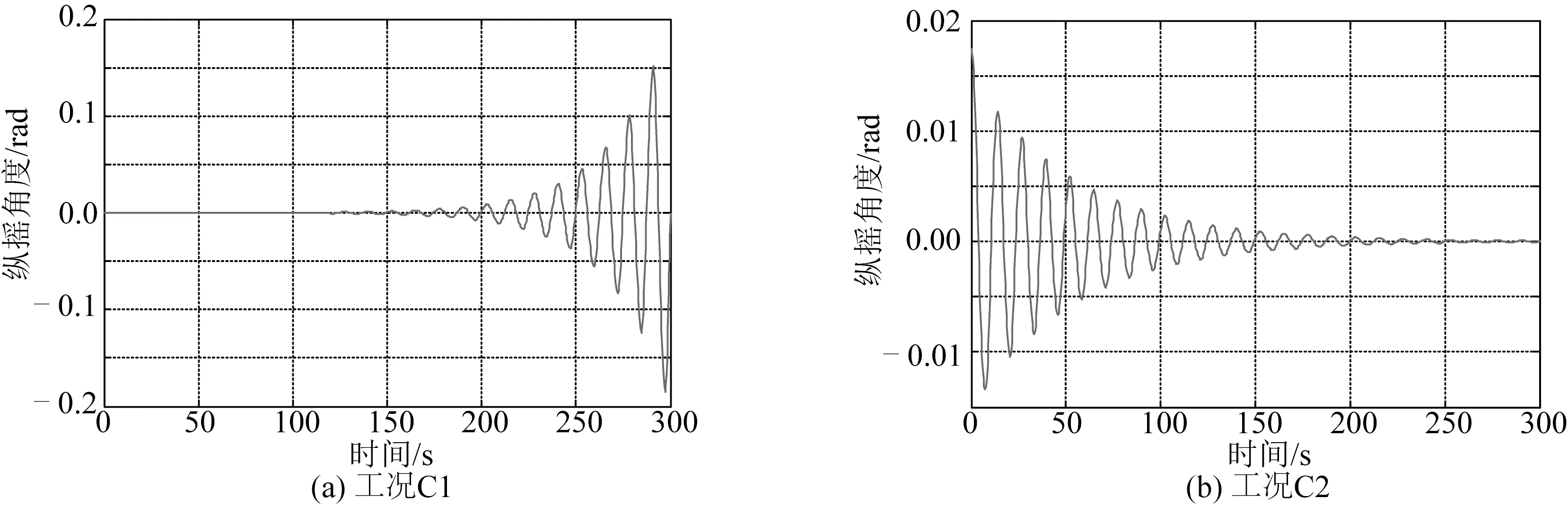
图7 工况C1、C2纵摇运动时程Fig.7 Pitch motion history of Cases C1 and C2

3 结 语

研究了深吃水半潜式平台(DDS)的参数共振问题，推导了DDS纵摇运动方程，运用希尔无穷行列式法求解了马修方程，给出了含阻尼的马修稳定性图谱，并结合具体算例讨论了不同参数对平台纵摇稳定性的影响，得出以下结论：

1)当平台垂荡运动周期接近纵摇运动固有周期一半时，纵摇运动容易发生参数共振现象。因此，在平台设计时，应使纵摇运动固有周期避开垂荡运动周期和波浪周期的2倍，使垂荡运动固有周期避开波浪周期，这样能够有效避免平台纵摇参数共振现象的发生。

2)减小平台垂荡运动幅值，可以有效抑制纵摇运动参数共振现象的发生。因此，在设计时应改善平台的垂荡运动性能，减小平台的垂荡运动。

3)增加系统阻尼可以减小不稳定区范围，从而有效抑制平台纵摇运动参数共振现象。因此，在平台设计时应尽量增加系统阻尼(如在平台底部加垂荡板)来减小参数共振发生的可能性。

[1] 姜哲,谢彬,谢文会.新型深水半潜式生产平台发展综述[J].海洋工程,2011,29(3):132-138.( JIANG Zhe,XIE Bin,XIE Wenhui.A review of novel semisubmersible production platforms[J].The Ocean Engineering,2011,29(3):132-138.( in Chinese ))

[2] Bindingsbo/A U,Bjo/rset A.Deep draft semi submersible[C]//Proceedings of the 21th International Conference on Offshore Mechanics and Arctic Engineering.2002:651-659.

[3] FRANCE W N,LEVADOU M,TREAKLE T W,et al.An investigation of head-sea parametric rolling and its influence on container lashing systems[J].Marine Technology,2003,40(1):1-19.

[4] SPYROU K J.Designing against parametric instability in following seas[J].Ocean Engineering,2000,27(6):625-653.

[5] NEVES M A S,RODRíGUEZ C A.Influence of non-linearities on the limits of stability of ships rolling in head seas[J].Ocean Engineering,2007,34(11-12):1618-1630.

[6] LU J,UUEDA N,MA K.Predicting parametric rolling in irregular head seas with added resistance taken into account[J].Journal of Marine Science and Technology,2011,16(4):462-471.

[7] HUSE E,KLEIVEN G,NIELSEN F G.Large scale model testing of deep sea risers[C]//Proceedings of the Offshore Technology Conference.1998:189-198.

[8] 杨和振,李华军.参数激励下深海立管动力特性研究[J].振动与冲击,2009,28(9):65-69.( YANG Hezhen,LI Huajun.Vibration analysis of deep-sea risers under parametric excitations[J].Journal of Vibration and Shock,2009,28(9):65-69.( in Chinese ))

[9] 肖飞,杨和振,卢其进,等.涡激致顶张力立管双频参量共振研究[J].海洋工程.2013,31(2):28-34.( XIAO Fei,YANG Hezhen,LU Qijin,et al.Vortex-induced parametric resonance of top tensioned riser based on bi-frequency excitation[J].The Ocean Engineering,2013,31(2):28-34.( in Chinese ))

[10] YANG H Z,XIAO F.Instability analyses of a top-tensioned riser under combined vortex and multi-frequency parametric excitations[J].Ocean Engineering,2014,81:12-28.

[11] HASLUM H A.Simplified methods applied to nonlinear motion of spar platforms[D].Trondheim:Norwegian University of Science and Technology,2000.

[12] RHO J B,CHOI H S,LEE W C,et al.Heave and pitch motions of a spar platform with damping plate[C]//Proceedings of the 12th International Offshore and Polar Engineering Conference.2002:198-201.

[13] KOO B J,KIM M H,RANDALL R E.Mathieu instability of a spar platform with mooring and risers[J].Ocean Engineering,2004,31(17-18):2175-2208.

[14] 王俊荣,谢彬.深水半潜式平台Mathieu不稳定问题研究[J].工程力学,2012,29(10):347-353.( WANG Junrong,XIE Bin.Mathieu instability study of a deepwater semi-submersible platform [J].Engineering Mechanics,2012,29(10):347-353.( in Chinese ))

Study on parametric resonance of a deep draft semi-submersible platform

MAO Huan,YANG Hezhen

(State Key Laboratory of Ocean Engineering,School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

P751

A

10.16483/j.issn.1005-9865.2016.01.003

1005-9865(2016)01-0018-07

2014-10-08

国家自然科学重点基金资助项目(50739004)；国家自然科学基金资助项目(51379005)

毛 欢(1989-)，男,研究生，主要从事海洋工程结构分析研究。

杨和振(1977-)，男，副教授，主要从事海洋工程结构分析研究。E-mail：yanghz@sjtu.edu.cn;yanghezhen@hotmail.com