应变软化对深部隧道围岩多层断裂的影响研究

许宇明

(湖南省高速公路管理局，湖南 长沙　410001)



应变软化对深部隧道围岩多层断裂的影响研究

许宇明

(湖南省高速公路管理局，湖南 长沙410001)

基于隧道围岩响应机理建立数值模型，以围岩峰后特征之一的塑性应变软化为目标，通过数值模拟揭示出在一定条件下，围岩中多层断裂现象的产生与其塑性应变阈值相对应。当围岩的塑性应变软化值低于其阈值时，围岩中应力的传递及应变响应与浅部经典围岩破裂规律迥异。然后进一步分析了应变软化值的大小对围岩中断裂层数、断裂总范围的影响，评估了多层断裂发生时围岩中切次生向应力与径向应力的相对关系，为深部岩体地下工程的开挖及支护设计提供了参考依据。

；隧道；围岩；深部；应变软化；多层断裂

0　引言

按围岩损伤程度及二次应力的大小，一般情况下开挖后隧道围岩依临空面由近至远依次出现松动带、塑性强化带、弹性带及原始状态区(如图1所示)。松动带中应力低于原岩应力，岩体裂隙发育，岩体质量劣化，是围岩荷载形成及支护对象的主体。目前岩体地下结构的支护设计思路都是该模式建立起来的。如支护锚杆所需长度、锚固持力层层位及最小围岩压力估算，等等。但随着工程往地层深处发展，在地下工程实践中专家们发现进入到地下一定深度后，围岩对开挖的响应不再遵从图1所示的模式，在有些深部地下工程围岩的断裂存在分层现象(如图2所示)。很显然，这种现象与经典的围岩响应模式(如图1)不同。随着深部地下工程实践的增多，图2所示的破裂现象也逐渐增多，同时也引起了很多著名专家和学者的关注并做进一步的研究。例如，文献[1]搜集了国内外关于分层断裂现象工程及研究的有关资料，总结得出围岩的分层断裂现象是深部地层与浅部地层对开挖反应的标志区别。文献[1～3]把分层断裂作为岩石工程是否进入深部的标准，并认为产生这种现象的重要原因之一是高的地应力转移所造成的劈裂效应。文献[4]以淮南矿区丁集煤矿深部巷道为工程背景，通过相似材料三维地质力学模型试验，再现了深部巷道围岩分区破裂的形成过程。文献[5]报道了利用钻孔电视和电阻率方法在煤矿的深部隧道围岩中监测到分层断裂现象。文献[6]通过有关钻进数据资料的分析，得出在金属矿山的深部隧道围岩中，也存在分层断裂。文献[7]从理论上探讨了分层断裂的力学原理，认为分层断裂主要是由于岩体是一种承受了多次地质历史运动的岩体，在力学上处于峰后阶段，是岩体的峰后特征导致了分层断裂行为的产生。因此，分层断裂的原因是岩体的峰后力学行为。峰后力学包括岩体力学性质软化、残余强度、剪涨性等等。因此，本文试图利用FLAC软件，通过数值方法进一步揭示岩体应变软化对深部隧道围岩分层断裂的影响，为深部隧道围岩压力估算、支护结构设计提供理论和实践参考依据。

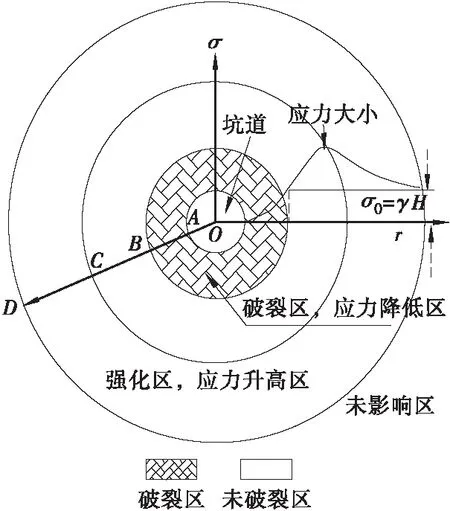
图1　隧道围岩响应典型模式

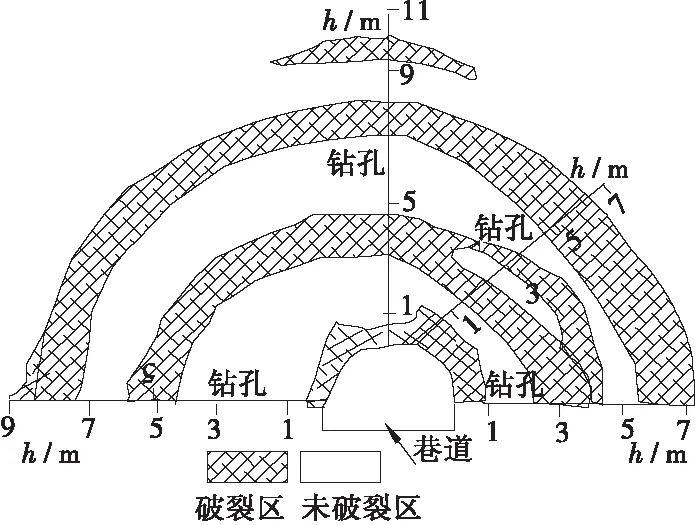
图2　深部地层隧道围岩分层断裂现象[1，2]

1　数值分析模型

1.1应变软化描述参数

应变软化显示岩体峰后力学性能的劣化，反映岩体在原有裂隙的基础上，各种新裂隙的扩展和贯通，是FLAC[8，9]数值模拟程序中表述岩体峰后性质的重要参数。该参数通过如下表达式确定：

(1)

内置的塑性参数eps增量表达式为：

(2)

1.2围岩力学参数及计算范围

围岩类型参照湘西山区武陵源某越岭深埋二级公路隧道选取。坑道围岩力学参数为：峰值粘聚力cp=0.54 MPa，残余粘聚力cr=0.37 MPa，峰值摩擦角φp=33°，残余摩擦角φr=25°，岩石剪切模量G=1.3×103MPa；泊松比v=0.22，天然地应力σ0=5.6 MPa。

为了与图1所示的经典响应破裂模式对照，在本研究中选用直径为4 m的规则圆形坑道，按照围岩响应范围，数值模型大小为隧道直径的3.5倍；根据轴对称原理，取其1/4，如图3所示。由深部地层地应力理论，天然应力设为三向等应力场，弧形外边界施加天然应力，垂直和水平边界法向位移约束。在位于垂直方向(90°)，水平方向(0°)设置了监测点，便于观察其两个方向上的应力传递及应变分布情况。

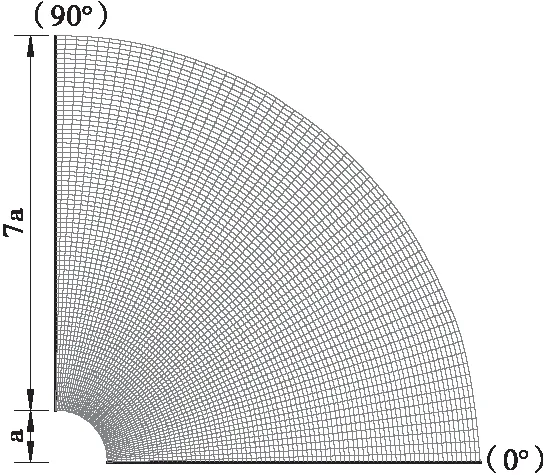
图3　数值计算模型

2　数值模拟过程及结果简析

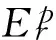
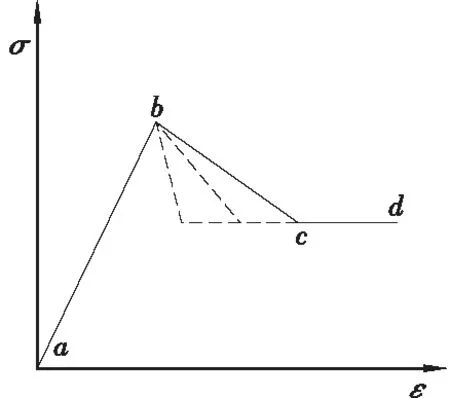
图4　不同峰后脆性示意图

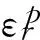
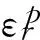
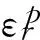
较早时期，有关学者[10]在相似模型试验及隧道监控中发现了类似的现象，如图7、图8是我国著名的深部工程岩石力学专家方祖烈教授于上世纪80年代末至九十年代初在我国西北的金昌镍矿深部地下工程研究中的有关实测及试验资料整理结果，也表明了这一现象的存在。

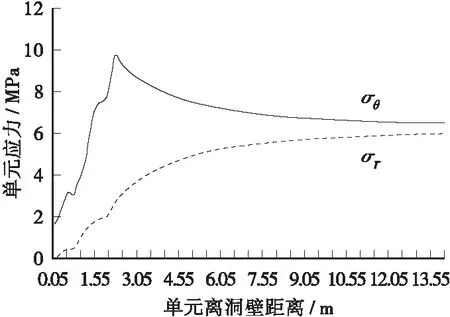
图=0.15，水平方向围岩径向、环向应力分布

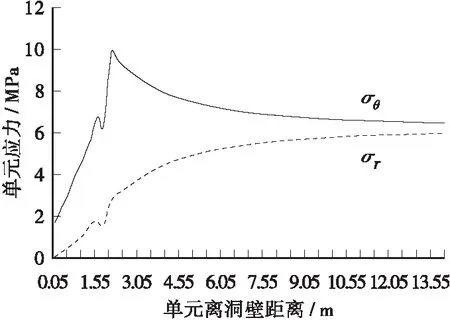
图=0.15，垂直方向围岩径向、环向应力分布

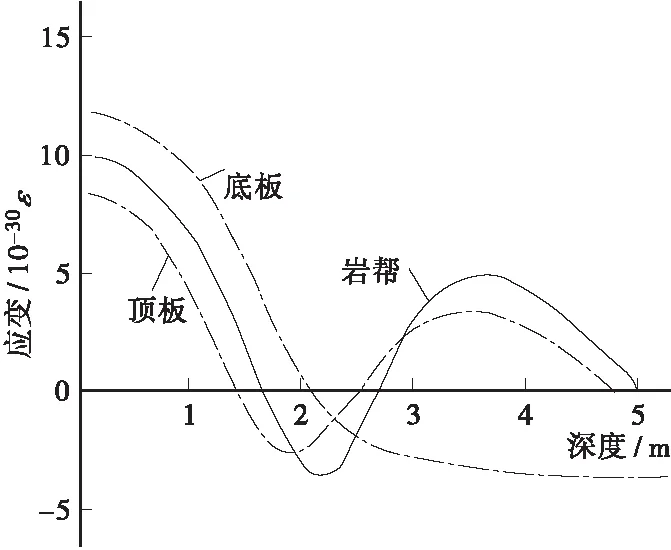
图7　深部巷道围岩变形相似模型实验[10]

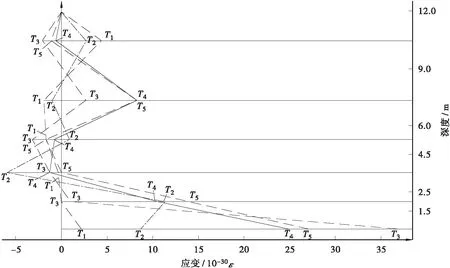
图8　深部巷道围岩拉压变形随时间变化[10]

图，围岩断裂分布情况

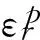
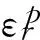
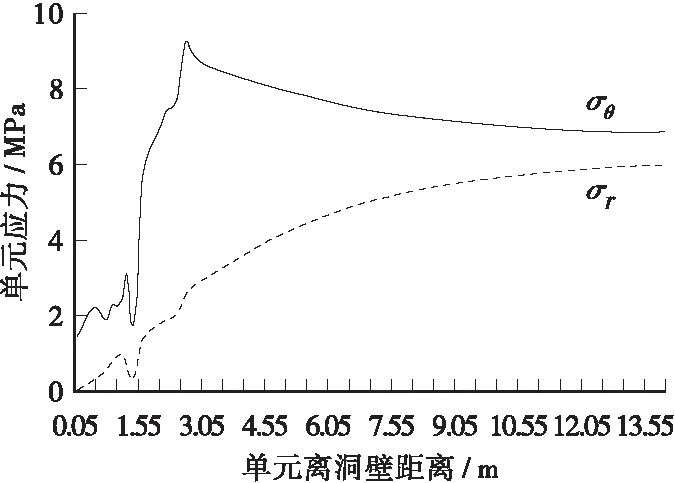
图=0.025，水平方向围岩径向、环向应力分布

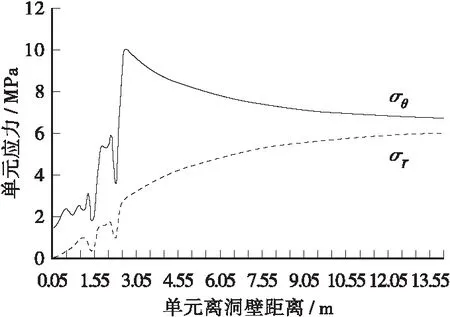
图=0.025，垂直方向围岩径向、环向应力分布

从图11～图14发现，围岩径向应力，切向应力分布曲线表现为：低应力→高应力→低应力→高应力反复交替出现，即在围岩中存在应力急剧变化区域，与经典模式的应力单调增长规律迥异。

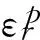
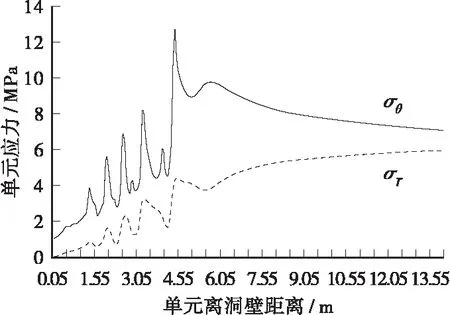
图，水平方向围岩径向、环向应力分布

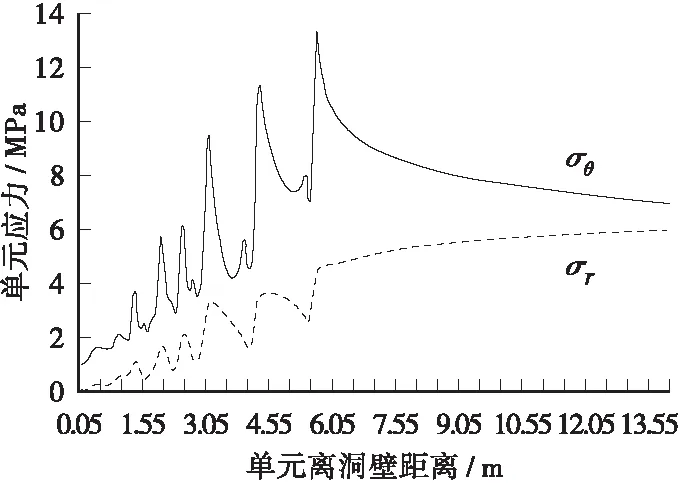
图，垂直方向围岩径向、环向应力分布

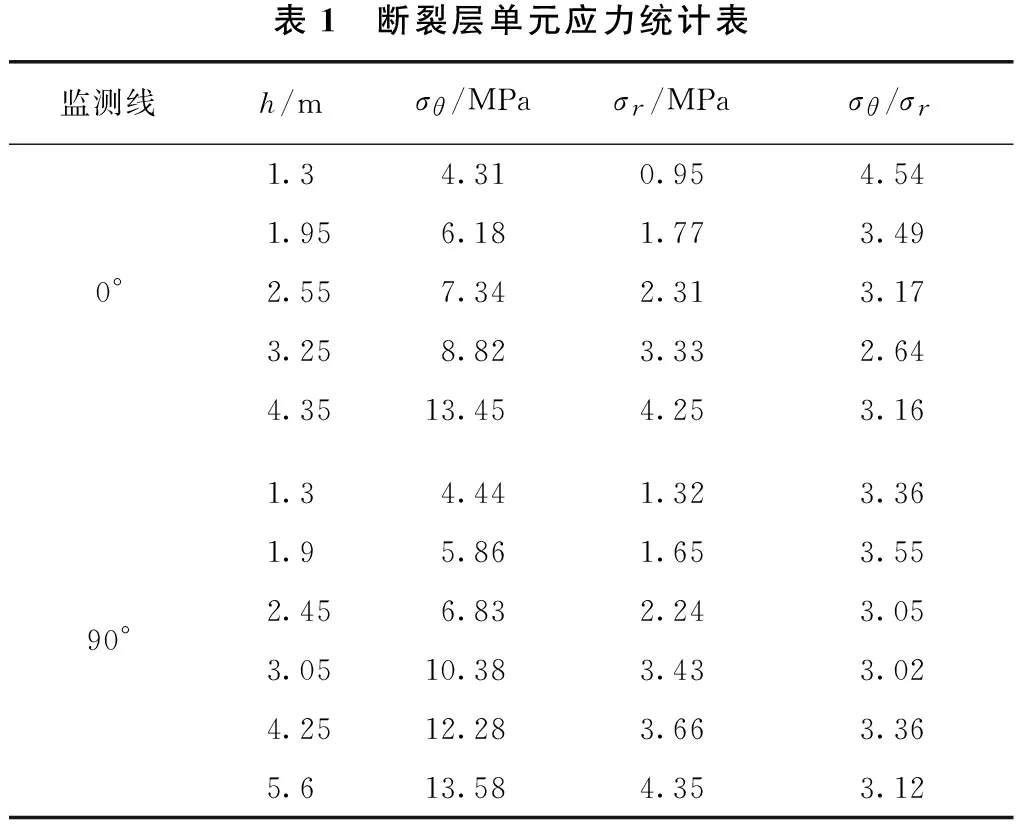
表1 断裂层单元应力统计表监测线h/mσθ/MPaσr/MPaσθ/σr0°1.34.310.954.541.956.181.773.492.557.342.313.173.258.823.332.644.3513.454.253.1690°1.34.441.323.361.95.861.653.552.456.832.243.053.0510.383.433.024.2512.283.663.365.613.584.353.12

3　结论

本文以围岩临界塑性剪切应变值表征围岩峰后软化强弱情况，采用FLAC数值软件，重点研究了应变软化对深部隧道围岩多层断裂的影响，主要结论如下：

1) 隧道围岩峰后软化强弱情况对围岩分层断裂现象具有重要影响，应变软化现象越强，多层断裂越易出现，对应于围岩临界塑性剪切应变值阈值约为0.15。

2) 深部隧道围岩中应力传递、应变分布的剧烈变化现象与岩石的峰后软化程度有关，围岩多层断裂的断裂层数、断裂总范围将随着围岩峰后应变软化现象增强而增加。

3) 随着围岩应变软化现象的增强，当径向应力和切向应力相对关系在3～4的范围内，围岩的多层环状断裂将贯通，因此可将该值作为围岩的多层破裂的判断依据之一。

本文仅研究了围岩软化这一峰后特征的影响，结果仅仅是初步的，深部及岩体的其他特征，如温度、岩体剪涨、膨胀系数等等将是有待进一步需要研究的问题。

[1]钱七虎.深部岩体工程的响应的特征科学现象及“深部”的界定[J].华东理工学院学报，2004，27(1)：1-5.

[2]钱七虎.非线性岩石力学新进展-深部岩体力学的若干关键问题[A].见：中国岩石力学与工程学会编.第八次全国岩石力学与工程学术大会论文集[M].北京：科学出版社，2004.

[3]王明洋，宋华，郑大亮，等.深部巷道围岩分区破裂机制及“深部”界定探讨[J].岩石力学与工程学报，2006，25(9)：1771-1777.

[4]张强勇，陈旭光，林波，等.深部巷道围岩分区破裂三维地质力学模型试验研究[J].岩石力学与工程学报，2009，28(9)：1757-1766.

[5]许宏发，钱七虎，王发军，等.电阻率法在深部巷道分区破裂探测中的应用[J]．岩石力学与工程学报，2009，28(1)：111-120.

[6]潘一山，李英杰，唐鑫，等.岩石分区碎裂化现象研究[J].岩石力学与工程学报，2007，26(S1)：3335-33341.

[7]宋华，汪新红，王明洋.对深部地下坑道围岩分区变形机理的探讨[J].解放军理工大学学报，2007，8(3)：274-279.

[8]刘波，韩彦辉(美).FLAC原理、实例与应用指南[M].北京：人民交通出版社，2005.

[9]陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京：中国水利水电出版社，2013.

[10]方祖烈.软岩巷道维护原理与控制措施[A].见：何满潮.中国煤矿软岩巷道支护理论与实践[M].北京：煤炭工业出版社，1996.

2016-06-07

许宇明(1982-)，男，工程师，主要从事高速公路管理工作。

；1008-844X(2016)03-0172-05

；U 451+.2

；A