套管错断井断口岩体损伤块度分布数学模型

刘国勇

（大庆石油国际工程公司，黑龙江大庆163453）

套管错断井断口岩体损伤块度分布数学模型

刘国勇*

（大庆石油国际工程公司，黑龙江大庆163453）

目前，套管错断井数量逐年增加，套管错断后，错断口岩体发生损伤破碎，并由错断口进入井眼内，影响油田正常生产，因此，错断井的修复工作意义重大。但由于岩体损伤破坏碎块度大小不一，很大程度上影响了修井施工中磨铣冲砂方案的制定，降低了冲砂效率，导致修井周期延长，成本增加。为了对套管错断井断口岩体破碎块度分布规律有一个较为精确的描述，基于概率论原理，从损伤岩体弹性纵波速度入手，运用分形几何理论，建立了新的计算岩块分形维数的方法，丰富了传统研究岩体破碎块度分布的理论，可以更方便快捷地预测岩体损伤块度分布，从而为套管错断井修井施工参数设计提供参考依据，指导现场施工快速高效的进行。

套管错断；岩体损伤；块度；分布；数学模型

近年来，许多专家学者在采矿、钻井工程方面已经对岩体损伤破坏块度分布进行了大量研究，但在套管错断井修井施工中还很少见到这一理论的研究。众所周知，磨铣冲砂作业是套管错断井修井施工中的一个重要环节，在磨铣冲砂作业时，由于对井筒内堆积岩块的块度大小认识不清，导致在冲砂和磨铣时间的制定与冲砂液密度的调配上一直没有理论上的指导，施工方案大多依据经验来制定。本文就是从这一问题入手，在理论上找出描述岩体破坏块度分布的方法，指导修井施工方案准确合理的制定。

1　岩体损伤块度分布函数

岩体破碎后岩块在几何形状和块度分布方法都具有统计自相似性，从分形角度描述岩体破碎过程如下：岩体最初破碎成有限个形状相似的次一级块体，这些次一级块体中的一部分又被破碎成形状相似的更次一级块体，此过程的每一次重复都产生更小的块体。根据岩体破碎概率和相似比以及不同粒级岩块的体积，可以得出：

式中：yk——块度小于或等于Rk的累积体积比；

Db——破碎岩块分形维数［1］。

2　岩体损伤破碎块度分布分形维数计算

以往求解岩体破碎块度分形维数时，多采用筛分的方法，这样会耗费大量的人力物力，本文提出了一种新的计算块度分形维数的方法。

2.1岩体损伤变量计算

岩体破碎后，内部存在着大量裂纹、孔隙等微观结构，超声波在岩体中是绕过裂隙纹、孔隙等传播的，从而延长了传播时间，降低了波速，因此可以根据岩体中纵波速度差异来判断岩体损伤程度，反映岩体内部微裂纹的发展状况，进而研究岩体超声波速度变化与损伤的关系。根据损伤岩体弹性纵波速度、损伤变量和岩体力学参数三者的关系，建立岩体损伤变量与超声波速度之间的定量关系［2］。

式中：cp0、cpi——岩体损伤前后弹性纵波速度，m/s。

岩体损伤前、后的弹性纵波速度可以通过超声波测量得到，因而可根据（2）式实现对岩体损伤度的实验测量。

2.2岩体块度分维数的计算

假设岩体损伤为立体损伤，将损伤岩体看作是由许多体积为δV的微元所构成，微元是岩体破裂的最小单元。以λ表示单位体积上含有损伤体元数目的数学期望，那么在体积为V的范围内出现K个损伤体元的概率可按泊松定律表示如下：

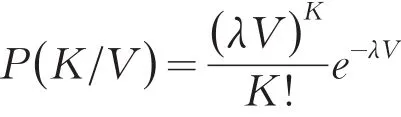
以P（V）表示在体积V内没有损伤的概率，以P1（ΔV）表示在ΔV内出现一个损伤体元的概率，则根据损伤体元概率所满足的泊松定律可得体积V内没有损伤的概率，进而得出体积V内有损伤体元的概率密度：

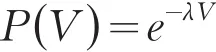
因而，在体积V内有损伤体元的概率为：

将（3）式对体积求导，可得岩体损伤体元的概率密度为：

若用Di来表示岩体的损伤变量（或称损伤因子），有下式成立：

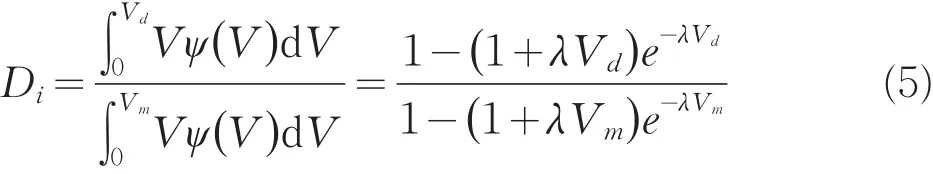
若用Di来表示岩体的损伤变量，如果令λ=1，Va则式（5）可表示为：

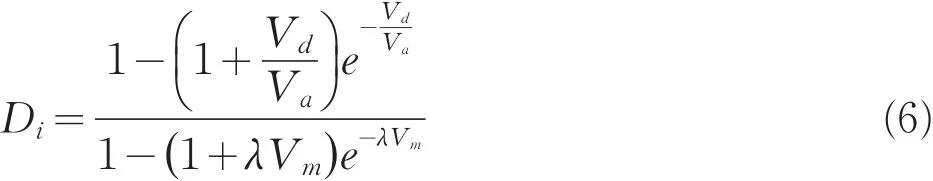
式中：Vm——岩体的总体积，m3；

Vd——岩体中的损伤体积，m3；

Va——岩体破碎后岩块的平均体积，m3；

λ——岩体中节理裂隙的数目［3］。隙密

根度的据关Y a系n g为等：的研究结果，岩体损伤因子与岩体裂

式中：γ——岩体裂隙密度［4］。

由式（7）可知，岩体裂隙密度为：

根据式（8），损伤岩体内裂隙的数目为：

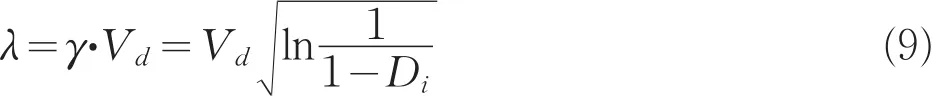
将式（9）代入式（6）可得：

根据岩体破碎块度分布函数，当筛下量y为50%时的块度尺寸为岩体破碎后岩体块度分布均值，记为Ra，则有：

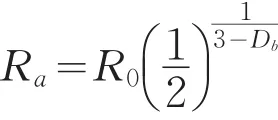
那么岩体破碎后的岩块平均体积为：

将式（11）代入式（10）得：

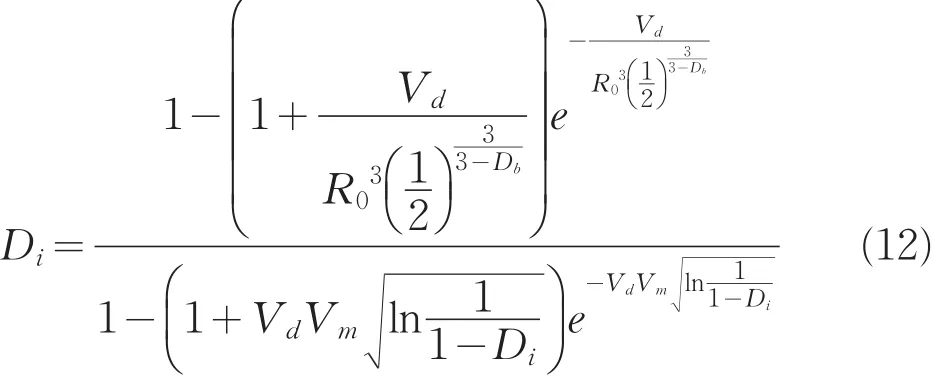
由损伤变量的定义：

代入式（12）整理得：

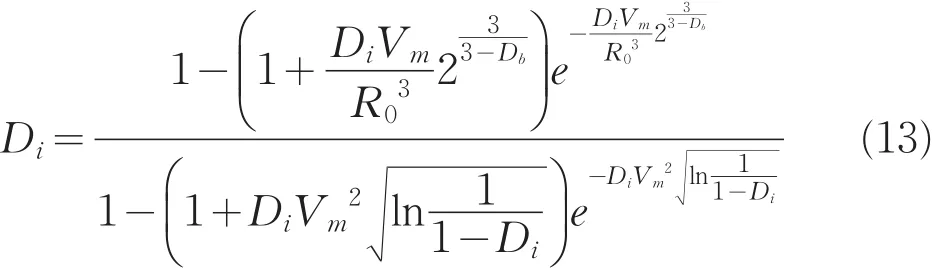
将式（2）代入式（13），整理得：

根据上式即可求出岩体损伤破碎后的块度分形维数［5］。

由式（14）可知，块度分形维数是岩体弹性纵波速度的函数，即：

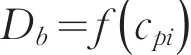
结合式（1），可得岩体破碎块度数学模型为：

3　岩体损伤块度模型的综合应用

3.1岩体损伤破碎块度分维数计算

在块度分布维数计算模型中，岩石在未损伤时弹性纵波速度为4500m，根据岩体损伤破碎块度分维数计算模型，就可以得到不同损伤程度下岩体弹性纵波速度与损伤变量和岩体块度分维数之间的关系，如图1所示。

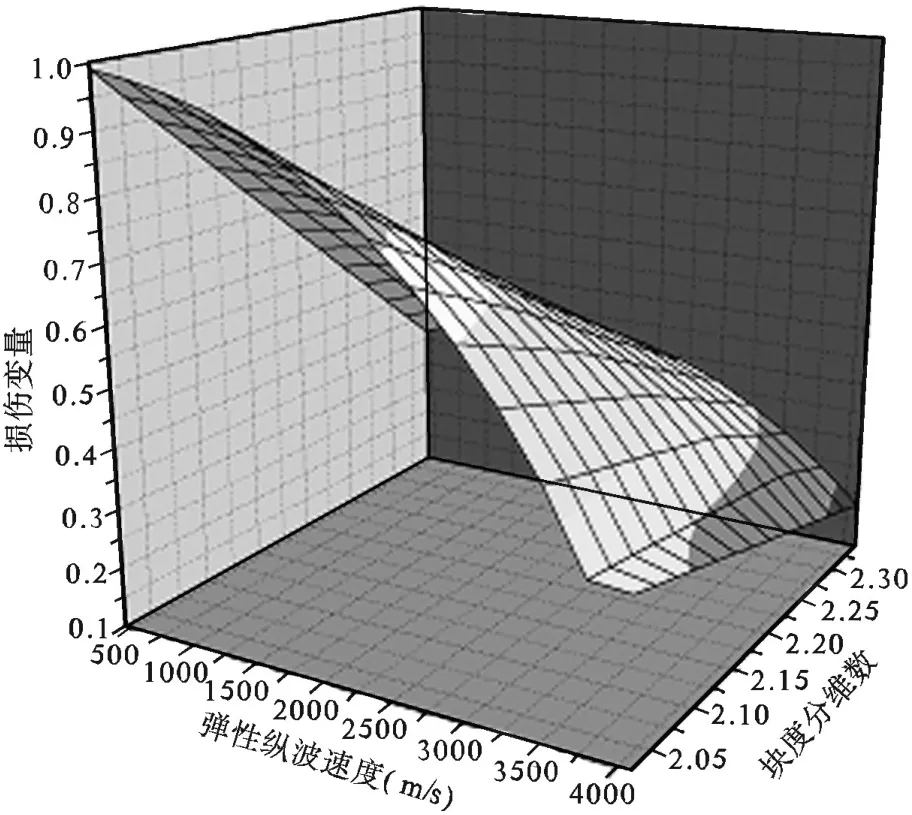
图1　岩体弹性纵波速度与操作变量及块度分维数关系

从图1可以看出，当岩体发生损伤后，岩体的弹性纵波速度与岩体的损伤变量呈非线性关系，弹性纵波速度越大，岩体损伤程度越小；岩体的弹性纵波速度与岩体破碎块度分维数呈非线性关系，岩体弹性纵波速度越大，块度分布维数越大。

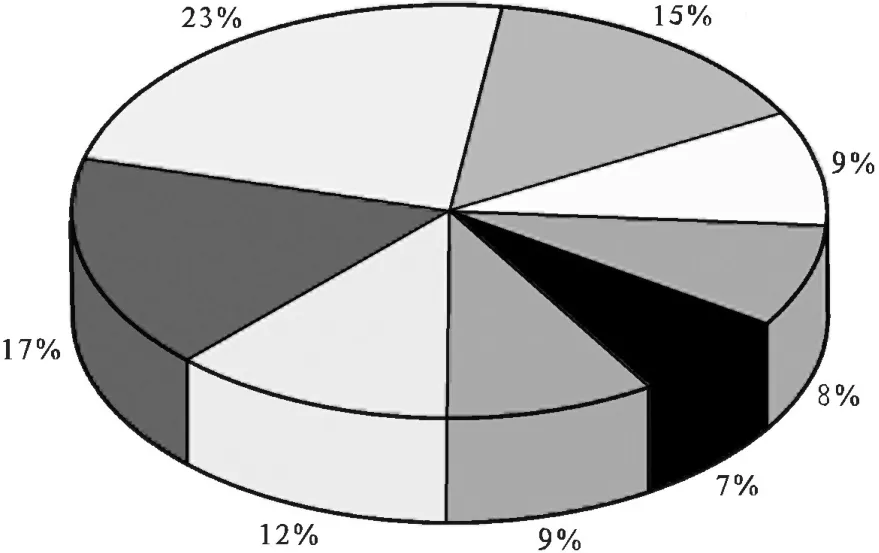
图2　不同尺寸岩块分布示意图

3.2岩体损伤破碎块度分布规律

当套管错断后，错断口岩体在井下巨大的压差作用下，发生失稳破碎，模拟井下条件，以套管错断口处的岩体为基础，进行岩石加载实验，并使用超声波检测技术测量损伤破坏后的岩体的弹性纵波速度，假设岩体破坏后，岩块的大块平均尺寸为60mm，弹性纵波速度为500m/s，代入破碎岩块块度分维数计算模型，可以得出在这种条件下的块度分形维数，结合块度分形维数与岩体破碎块度累积量的关系式，可以得出破碎岩块累积体积百分数曲线与不同块度等级所占的体积百分数。

将损失破碎后的岩块按＜5mm，5～10mm，10～15mm，15～20mm，20～30mm，30～40mm，40～50mm，＞50mm八个尺寸等级进行计算分析，每个尺寸等级所对应的体积百分数不同，分别为7%，9%，12%，17%，23%，15%，9%，8%，如图2所示，破碎块度尺寸在15～30mm之间的体积累积百分数比重较大，说明岩体破碎后粒径大小多在此范围内，岩块尺寸等级分布整体基本呈二次抛物线形式。

4　结论

（1）引入损伤岩体弹性纵波速度，建立岩体块度分维数计算模型，提出一种计算岩体破碎块度分布的方法。

（2）当岩体发生损伤破坏后，岩体的弹性纵波速度与岩体破碎块度分维数呈非线性关系，岩体弹性纵波速度越大，块度分布维数越大。

（3）岩体破坏后，每个尺寸等级所对应的体积百分数不同，中间尺寸等级岩块体积百分数比重较大，整体基本呈二次抛物线形式。

［1］张继春.岩体爆破的块度理论及其应用［M］.西南交通大学出版社，2001：52-54.

［2］Grady D E，Kipp M E.Dynamic Rock Fragmentation.In：Atkinson B K eds，Fracture Mechanics of Rock，San Diego，California：Academic Press，1987：429-475.

［3］赵斌，于亚伦.损伤岩体破碎块度分布的预测［J］.金属矿山，1997（5）：17-19.

［4］Yang R，Bawden W F，Katsabanis P D.A New Constitutive Model for Blast［J］.Int J Mech Min Sci&.Geomech Abstr，1996，33（3）：245-254.

［5］Zhao Zhongyan，et al.Fractal Analysis Applied to Calculastic Rocks［J］.Technoloph-ysics，1990，178：373-377.

TE931

A

1004-5716（2016）10-0024-03

2015-12-03

2015-12-08

国家自然科学基金（水力压裂岩体损伤演化与微裂缝形成机理研究No.50974028）。

刘国勇（1983-），男（汉族），山东东明人，工程师，现从事石油钻掘技术工作。