基于多理论组合决策的矿山安全绩效评价规律分析
田森,陈建宏
基于多理论组合决策的矿山安全绩效评价规律分析
田森1, 2, 3,陈建宏2
(1. 重庆大学煤矿灾害动力学与控制国家重点实验室,重庆,400030;2. 中南大学资源与安全工程学院,湖南长沙,410083;3. 重庆大学资源及环境科学学院,重庆,400030)
以矿山安全绩效评价及其规律为研究对象,将矿山安全指标分为状态指标与绩效指标。通过多种理论组合构建模型对矿山安全绩效做出评价,并对安全绩效评价的内在规律进行分析。综合矿山的5个安全绩效评价指标,考虑指标值为区间数的情况,利用灰色区间关联聚类理论构建模型对20个样本矿山的安全绩效进行聚类分析与评价。将矿山安全绩效评价作为决策属性,安全状态指标作为条件属性,考虑到属性中含有的偏好信息,利用优势关系粗糙集与粗糙近似决策理论对矿山安全绩效评价规律进行分析,将各安全状态指标与安全绩效评价之间的内在关系加以揭示。研究结果表明:多理论组合决策模型能够对矿山安全绩效进行评价并揭示其内在规律,可为矿山安全生产工作提供指导与借鉴。
矿山;安全绩效;灰色关联;粗糙近似;优势关系;粗糙集
为了防治矿山灾害事故的频繁发生,对矿山安全进行评价一直是主要对策之一。安全评价是对矿山生产的各环节或整体做出安全性评估与评价,为矿山采取相应对策提供依据。以往对矿山的安全评价,大多只是对矿山安全状态的评价,而忽视了对安全绩效的评价,实际上,矿山安全状态可视为矿山安全的各类投入的集合,而矿山安全绩效则相当于矿山安全的结果,分析矿山安全状态与安全绩效之间的规律,对矿山安全建设很有意义[1−2]。对于矿山安全的绩效评价而言,其指标因素是随时间而在一个区间内变动的数值,为灰数。而传统的模糊评价、层次分析以及其他一些评价方法又无法对指标因素值为区间数的情况做出处理,因此只能对各指标因素某一个时间段的值取平均值进行处理,虽然简化了过程,但与真实情况不符,其绩效评价结果必然与真实情况存在一定程度的偏差。对于矿山安全绩效评价含有区间数这种灰色不确定性的情况,灰色区间关联聚类分析方法[3−7]可以对数据库中的“贫信息”数据进行分析和挖掘,解决含有区间数这种灰色信息的多指标评价问题,而且该聚类分析方法采用区间数来描述问题并进行聚类分析,可以准确地表示和保存有用信息,避免了聚类过程中的信息失真。而对于矿山安全状态指标与安全绩效评价之间的关系或规律,可用粗糙近似决策[8]及基于优势关系的粗糙集理论进行分析[9]。粗糙近似决策能够对决策对象或决策目标在认知程度有限或认知模糊情况下进行近似分类发现,对象之间的不可分辨关系。而优势关系的粗糙集是用优势关系来代替不可分辨关系的粗糙集理论[10−11]。它不仅综合全面地考虑了各矿山安全状态指标,而且对指标因素中的偏好信息也加以考虑,可用来进行矿山安全状态指标与安全绩效之间的规律分析。
1 系统建模
1.1 系统指标构建
矿山安全评价包含安全状态指标体系和安全绩效指标体系2套指标体系。
1) 安全状态指标体系。矿山安全状态指标可归纳为人的因素1、机械设备因素2、管理制度因素3、环境因素4以及技术因素55个方面,即一级指标,一级指标又可以细分为安全技能1、安全意识2、设备安全性能3等11个二级指标[12]。矿山安全状态指标体系见图1,其中,安全生产投入率为安全投入与项目总造价之比。

图1 矿山安全状态指标
2) 安全绩效指标体系。安全绩效指标可以分为事故损失1和工伤事故率2。事故损失1包括经济损失1和工时损失2,工伤事故率2又包括轻伤事故率3、重伤事故率4以及万人死亡率5等[13−14]。
1.2 矿山安全绩效评价灰色区间关联分析
由个矿山构成的样本矿山集合={1,2,…,},由5个矿山安全绩效指标构成集合={1,2,3,4,5},则矿山的安全绩效指标d为区间数,矿山的安全绩效量化评估向量为
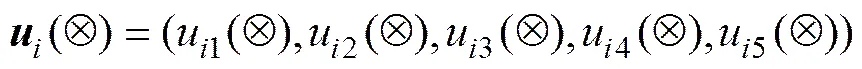
灰色区间关联分析步骤如下:
步骤1) 利用灰色极差变换公式对矿山安全绩效指标d的值进行变换。
效益型指标(值越大绩效评价越好指标)极差变换公式为
成本型指标(值越小绩效评价越好指标)极差变换公式为

步骤2) 根据最优化处理公式



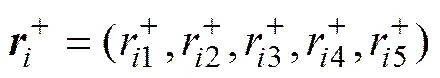
由此生成样本矿山集合对象关于理想对象的灰色区间关联系数矩阵。
步骤4) 根据需要划分个灰类,将样本矿山集合的安全绩效指标d的灰色区间关联系数值范围分为个小区间,并构建安全绩效指标d关于灰类的白化权函数(=1,2,…,)。
步骤5) 确定指标d的指标权重η。为避免在指标权重计算时人为因素的干扰,以各指标的灰色关联系数为基础,由下式计算出指标d的指标权重η。
步骤6) 计算矿山的安全绩效关于灰类的综合聚类系数(=1,2,…,;=1,2,…,):
根据下式判断出矿山的安全绩效各灰类的综合聚类系数的最大值属于灰类*,得到矿山安全绩效综合评价,
步骤7) 对矿山进行粗糙近似决策分析[15]。据此生成矿山安全绩效评价的粗糙近似决策。
1.3 安全绩效评价规律的优势关系粗糙集分析
利用优势关系粗糙集理论对的安全绩效与安全状态指标之间的规律进行分析[16]。
步骤1) 将样本矿山集的安全绩效综合评价作为矿山安全状态与绩效评价规律分析的决策属性,将矿山安全状态指标集合作为条件属性,得到矿山安全状态与绩效评价规律分析知识系统=(,,,)。其中为V的并集,V为属性的值域。
步骤2) 采用合适的数据离散方法对评价决策表进行离散化处理。得到的矿山安全状态与绩效评价规律分析带有偏好信息的偏好决策表。
步骤3) 按照偏好决策表中的决策属性(矿山安全绩效评价),可分为若干偏好顺序类,得到偏好决策类的并集。
步骤4) 应用适当的约简算法搜寻最优约简,利用最优约简对安全绩效进行评价。
步骤5) 根据最优约简属性生成规律分析的最少偏好决策规则集≥与≤[17]。
系统建模流程图见图2。

图2 系统建模流程
2 实证分析
2.1 背景简介
某成矿带上有几十家矿山。一直以来,由于矿山企业不了解对人员意识、机械设备以及管理制度等矿山安全投入等方面对矿山安全绩效的内在影响,造成很多矿山企业的安全投入与安全绩效不成正比。很多企业在投入了大量人力、物力、财力对安全工作进行改进后,安全事故仍然频发,造成工时及经济损失很大,人员伤亡严重。为了有针对性地对矿山安全工作部署与改进,以取得较好的矿山安全效益,亟待科学地对矿山安全投入与绩效进行分析。
选取该区域一批有代表性的矿山企业,统计2000 —2013年各矿山企业历年的安全投入(即安全状态)指标,其中,安全技能1为定性指标,分为高、中、低;安全意识2为定性指标,分为强、一般、差;设备安全性能3为定性指标,分为好、中、差;防护设备装备4为定性指标,按企业配备的数量分为多、中、少;安全生产组织5为定性指标,按严密程度分为严密、一般、松散;安全生产制度6为定性指标,按完备程度分为完善、较完善、欠缺;安全生产投入率7为定量指标;潜在危险源数量8为定性指标,分为大、中、小;可能事故的严重性9为定性指标,分为严重、较严重、轻微;工艺流程安全性10为定性指标,分为安全、较安全、危险;安全技术措施11为定性指标,按照与矿山企业的适应程度,分为合理、较合理、不合理。得到各矿山企业的安全投入即安全状态指标见表1。统计得到各矿山历年安全绩效区间数指标值见表2。
表1 矿山安全状态指标
Table 1 State indexes of mine safety

注:各安全状态指标属性或值为各指标历年的平均综合评价或计算结果。
表2 矿山安全绩效指标
Table 2 Performance state indexes of mine safety

2.2 安全绩效评价分析
对于表2中的各矿山的安全绩效评价指标,统计得到经济损失1的上限为124.1万元,下限为3.2万元;工日损失2的上限为151工日,下限为3工日;轻伤事故率3的上限为283次,下限为7次;重伤事故率4的上限为61次,下限为0次;死亡率5的上限为59.3万−1,下限为0。各指标为成本型指标,故采用式(2)中的极差变换公式进行标准化处理,得到矿山安全绩效指标标准化的灰色信息见表3。
表3 矿山安全绩效指标标准化灰色信息
Table 3 Gray standardized information of mine safety performance indexes

根据表3可知:对于经济损失指标,各矿山上下限差值为0.14~0.55万元;对于工时损失指标,各矿山上下限差值为0.14~0.55工日;对于轻伤事故率指标,各矿山上下限差值为0.28~0.88次;对于重伤事故率指标,各矿山上下限差值为0.28~0.92次;对于死亡率指标,各矿山上下限差值为0.15~1.00万−1。这说明对于某些矿山的历年安全绩效指标而言,不同年份间的差距有时还是很大的。
利用式(3),得到理想矿山安全绩效的评估向量为

按照表3中的各矿山安全绩效指标的标准化灰色信息,利用式(4)计算得到关于理想矿山安全绩效的灰色区间关联系数见表4(参照常例,分辨系数取为0.5)。
表4 灰色区间关联系数
Table 4 Gray interval correlation coefficient table

根据表4可知:经济损失的灰色区间关联系数为0.34~1.00;工时损失的灰色区间关联系数为0.43~0.94;轻伤事故率的灰色区间关联系数为0.52~0.96;重伤事故率的灰色区间关联系数为0.48~1.00;死亡率的灰色区间关联系数为0.42~1.00。这说明对于某一安全绩效指标,各矿山的差距还是很大的,各矿山的安全工作所取得的成效还是有较大差异的。
根据各矿山安全绩效指标的灰色区间关联系数,按照等距离区分原则,构建安全绩效评价为差、较差、一般、较好、好5个灰类的白化权函数如下:
差:
较差:
一般:
较好:
好:
根据白化权函数计算得到各矿山的各类安全绩效指标的各灰类权数。
以表4中的数据为基础,参照式(5)得到经济损失1、工时损失2、轻伤事故率3、重伤事故率4和死亡率5各指标权重分别为0.136 8,0.198 6,0.254 6,0.225 6和0.184 4。
以各矿山的各类安全绩效指标的各灰类权数以及各指标权重为基础,参照式(6)得到各矿山安全绩效相对于各灰类的综合聚类系数及最大综合聚类系数及其相应的灰类属性见表5。
表5 矿山安全绩效综合聚类系数
Table 5 Integrated clustering coefficient of mine safety performance

根据表5得到3个灰类集合:一般类集合1={2号,3号,6号,9号,11号,16号,17号};较好类集合2={7号,8号,10号,12号,14号,18号,19号,20号};好类集合3={1号,4号,5号,13号,15号}。集合{1,2,3}构成矿山安全绩效上的一个划分,对应生成等价关系,满足/={1,2,3}。
选取矿山安全生产投入率7作为粗糙近似决策分类背景,按照等宽度区间法进行离散,宽度为[0.68%,2.26%)的为低安全投入率1;宽度为[2.26%,3.84%)的为中安全投入率2;宽度为[3.84%,5.42%]的为高安全投入率3。1,2和3相当于安全生产投入率7的取值范围[0.68%,5.42%]的3个子集。
得到相应的粗糙近似决策规则如下:

,
,,

,,
,
式中:egR为负区;nR为边界区;为下近似;为上近似。
由粗糙近似决策可以看出:安全绩效好的安全生产投入率都高;而安全生产投入率高的安全绩效有可能好,也有可能较好,不会为一般;安全生产投入率中或低的安全绩效为一般或较好,不可能为好。
2.3 优势关系粗糙集分析
对表1中的矿山安全生产投入率指标按照前文所述的等宽度区间法进行离散,以表1中的矿山安全状态指标作为条件属性,以矿山安全绩效评价的灰类属性作为决策属性,构建出矿山安全绩效分析的评价决策表。
按照矿山安全绩效评价的决策属性,可分为3个偏好顺序类:l,1={一般},l,2={较好},l,3={好}。根据偏好顺序类划分论域,得到如下决策类的并集:
应用遗传算法对条件属性进行约简,可搜寻到5个最优约简:{1,6,7,8,10},{1,2,6,7,8},{1,4,6,7,8},{1,6,7,8,9}及{1,6,7,8,11},可由以上约简生成偏好规则。其中{1,6,7,8}为各约简的共有属性,即为约简的核。
选择一种最优约简,生成偏好规则。选取最优约简{安全技能1,安全生产制度6,安全生产投入率7,潜在危险源数量8,工艺流程安全性10}生成至少偏好规则≥见表6,生成至多偏好规则≤见表7。
表6≥概率决策规则集
Table 6≥probability decision rules

表7≤概率决策规则集
Table 7≤probability decision rules

由表6和表7可以看出:至少决策规则集≥生成的规则覆盖率100%,且没有出现规则之间的矛盾,分类全部正确,分类质量很高;而至多决策规则集≤的规则支持数高于对象数,说明某些对象至少从属于2种规则,分类质量不高。故选取表6的至少决策规则集≥作为决策分析,选取支持数为5及以上的规则作为安全绩效评价分析规则。
表6中的规则解释如下:
规则1):当安全技能高、安全生产制度至少较完善、安全生产投入率高、潜在危险源数量小以及工艺流程安全性安全时,矿山安全绩效评价为好;
规则2):当安全技能为中以上、安全生产制度至少较完善以及安全生产投入率为中以上时,矿山安全绩效评价至少为较好;
规则3):当安全生产投入率为中以下,且工艺流程安全性为危险时,矿山安全绩效评价为一般。
2.4 结果分析
根据分析结果可知:编号为1号,4号,5号,13号,15号的矿山安全绩效评价为好;编号为7号,8号,10号,12号,14号,18号,19号,20号的矿山安全绩效评价为较好;编号为2号,3号,6号,9号,11号,16号,17号的矿山安全绩效评价为一般。在安全状态指标体系中,安全技能、安全生产制度、安全生产投入率以及潜在危险源数量是影响矿山安全绩效评价的最重要的指标因素。矿山安全绩效分析的至少决策规则集≥,生成规则集中,支持数大,覆盖率高,且分类正确,可选取支持数大的规则作为规律使用,矿山企业在以后的实践中可参照相应规律进行有重点及针对性地部署安全生产工作。
针对安全评价为一般的矿山,对其部署安全生产工作时,重点对安全技能、安全生产制度、安全生产投入率、潜在危险源数量以及工艺流程安全性指标进行改进之后,这些矿山发生的安全生产事故大为减少,安全生产事故所造成的后果的严重程度也大为降低。
3 结论
1) 针对选取的20个样本矿山的5个安全绩效评价指标的区间灰数值,利用灰色区间关联聚类分析理论对矿山的安全绩效进行了聚类分析,得到了“一般”、“较好”及“好”3个综合灰类,克服了一般的聚类分析理论无法对灰色区间数指标体系进行聚类分析的缺点。得到综合评价为“好”的矿山有5个,综合评价为“较好”的矿山有8个,综合评价为“一般”的矿山有7个。
2) 安全技能1、安全生产制度6、安全生产投入率7和潜在危险源数量8等4项指标是评价矿山安全绩效的核心因素。在进行矿山安全绩效投入时,应将这4项因素作为重点。
3) 利用优势关系粗糙集理论生成的至少决策规则集≥,选取了支持数为5,8,5的3条规则作为矿山安全绩效评价的规律。相对于传统的不可分辨关系粗糙集生成的决策规则集而言,其规则支持数大、分类质量高,可靠性与准确性均相对较高。
[1] 张舒, 史秀志, 古德生, 等. 基于 ISM 和 AHP 以及模糊评判的矿山安全管理能力分析与评价[J]. 中南大学学报(自然科学版), 2011, 42(8): 2406−2415. ZHANG Shu, SHI Xiuzhi, GU Desheng, et al. Analysis and evaluation of safety management capability in mine based on ISM and AHP and fuzzy evaluation method[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2406−2415.
[2] 罗云, 程五一. 现代安全管理[M]. 北京: 化学工业出版社, 2009: 7−20. LUO Yun, CHENG Wuyi. Modern safety management[M]. Beijing: Chemical Industry Press, 2009: 7−20.
[3] 董卓宁, 卢俊言, 肖霄. 基于灰色区间关联的UCAV 自主决策方法[J]. 北京航空航天大学学报, 2013, 39(11): 1536−1541. DONG Zhuoning LU Junyan XIAO Xiao. Decision-making approach to UCAV based on gray interval relative theory[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(11): 1536−1541.
[4] ZHANG Wenxiu. Incomplete information system and its optimal selection[J]. Computer and Mathematics with Application, 2010, 48(5/6): 691−698.
[5] YANG Xibei, XIE Jun, SONG Xiaoning, et al. Credible rules in incomplete decision system based on descriptor[J]. Knowledge based Systems, 2009, 22(1): 8−17.
[6] 骆文辉, 刘少伟, 杨建军. 基于灰色区间关联决策的目标威胁评估[J]. 空军工程大学学报(自然科学版), 2008, 9(3): 37−41. LUO Wenhui, LIU Shaowei, YANG Jianjun. Threat evaluation technology based on grey interval-number for grey decision-making[J]. Journal of Air Force Engineering University (Natural Science Edition), 2008, 9(3): 37−41.
[7] GU Hui, SONG Bifeng. Study on effectiveness evaluation of weapon systems based on grey relational analysis and TOPSIS[J]. Journal of Systems Engineering and Electronics, 2009, 20(1): 106−111.
[8] 吴顺详. 灰色粗糙集模型及其应用[M]. 北京: 科学出版社, 2009: 113−119. WU Shunxiang. Gray rough set model and its application[M]. Beijing: Science Press, 2009: 113−119.
[9] 菅利荣. 面向不确定性决策的杂合粗糙集方法及其应用[M]. 北京: 科学出版社, 2008: 57−81.JIAN Lirong.Facing the heterozygous uncertainty decision-making rough set method and its application[M]. Beijing: Science Press, 2008: 57−81.
[10] 罗凯, 吴超, 阳富强. 基于优势关系粗糙集与灰靶决策的矿石自燃管理应对体系[J]. 中南大学学报(自然科学版), 2014, 45(1): 224−230. LUO Kai, WU Chao, YANG Fuqiang. Management response system to ores spontaneous combustion based on dominance based rough sets and grey target[J]. Journal of Central South University (Science and Technology), 2014, 45(1): 224−230.
[11] 周献中, 黄兵, 李华雄, 等. 不完备信息系统知识获取的粗糙集理论与方法[M]. 南京: 南京大学出版社, 2010: 121−144.ZHOU Xianzhong, HUANG Bing, LI Huaxiong, et al. Rough set theory and method of incomplete information systems knowledge acquisition[M]. Nanjing: Nanjing University Press, 2010: 121−144.
[12] 刘素霞, 梅强, 沈斌, 等. 安全绩效研究综述[J]. 中国安全科学学报, 2010, 20(5): 131−138. LIU Suxia, MEI Qiang, SHEN Bin, et al. Literature review on safety performance[J]. China Safety Science Journal, 2010, 20(5): 131−138.
[13] 张杰. 金属非金属地下矿山安全绩效考评研究[D]. 武汉: 武汉理工大学资源与环境工程学院, 2013: 10−40. ZHANG Jie. The research on safety performance evaluation in metal and nonmetal underground mines[D]. Wuhan: Wuhan University of Technology. School of Resources and Environment Engineering, 2013: 10−40.
[14] 齐蕊. 地下金属矿山企业安全绩效评估研究[D]. 北京:中国地质大学(北京)工程技术学院, 2009: 10−40. QI Rui.Study on safety performance evaluation of underground gold mine enterprise[D]. Beijing: China University of Geosciences (Beijing). School of Engineering and Technology, 2009: 10−40.
[15] 衣晓, 张怀巍. 极坐标系下的航迹灰色区间关联算法[J]. 舰船电子工程, 2012, 32(8): 45−47. YI Xiao, ZHANG Huaiwei. Gray track correlation algorithm based on the polar coordinate interval numbers[J]. Ship Electronic Engineering, 2012, 32(8): 45−47.
[16] 张文修, 仇国芳. 基于粗糙集的不确定决策[M]. 北京: 清华大学出版社, 2005: 3−25. ZHANG Wenxiu, QIU Guofang.Based on rough sets of uncertain decision[M]. Beijing: Tsinghua University Press, 2005: 3−25.
[17] 程温鸣, 彭令, 牛瑞卿. 基于粗糙集理论的滑坡易发性评价: 以三峡库区秭归县境内为例[J]. 中南大学学报(自然科学版), 2013, 44(3): 1083−1090. CHENG Wenming, PENG Ling, NIU Ruiqing. Landslide susceptibility assessment based on rough set theory: taking Zigui County territory in Three Gorges Reservoir for example[J]. Journal of Central South University (Science and Technology), 2013, 44(3): 1083−1090.
(编辑 赵俊)
Law analysis of performance evaluation for mine safety based on combinatorial decision by multiple theories
TIAN Sen1, 2, 3, CHEN Jianhong2
(1. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400030, China;2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;2. School of Resources and Erosion Mental Science, Chongqing University, Chongqing 400030, China)
Taking mine safety performance evaluation and laws for the study, the indexes of mine safety were divided into state indexes and performance indexes. Multiple theories were combined to build a model to evaluate mine safety performance, and analyze the inherent law of mine safety performance evaluation. Five indexes which evaluate mine safety performance were integrated, the situation that the values of indexes were interval numbers was taken into account, gray interval associated cluster was applied to build the model for clustering analysis and evaluating safety performance of 20 sample mines. Mine safety performance evaluation was taken as decision attribute, state indexes were taken as condition attributes, and the preference information contained in attributes was also taken into account, dominance-based rough set and rough approximation were applied to analyze the law of performance evaluation for mine safety, and intrinsic relationship between each safety state indexes and performance evaluation was revealed. The results show that decision model combined by multiple theories can evaluate the performance of the mine safety and reveal its inherent laws, and can provide guidance and reference for the safety of mine production.
mine; safety performance; gray relational; rough approximation; dominance relation; rough set
10.11817/j.issn.1672-7207.2016.06.035
TD05
A
1672−7207(2016)06−2073−10
2015−06−09;
2015−09−20
国家自然科学基金资助项目(51374242);全国优秀博士学位论文专项资金资助项目(200449);中南大学自由探索计划项目(2012QNZT028)(Project(51374242) supported by the National Natural Science Foundation of China; Project(200449) supported by the National Outstanding Doctoral Dissertations Special Fund of China; Project(2012QNZT028) supported by the Free Exploration Fund of Central South University)
田森,博士,从事矿山安全技术方面的研究;E-mail:115501019@csu.edu.cn

