自由下落抛锚时锚的运动数学模型
于 洋, 房家胜, 姜海波, 2
(1. 大连海事大学 航海学院, 辽宁 大连 116026; 2. 中海客轮有限公司 安全管理部, 辽宁 大连 116003)
YU Yang1, FANG Jiasheng1, JIANG Haibo1, 2
自由下落抛锚时锚的运动数学模型
于 洋1, 房家胜1, 姜海波1, 2
(1. 大连海事大学 航海学院, 辽宁 大连 116026; 2. 中海客轮有限公司 安全管理部, 辽宁 大连 116003)
为研究锚下落速度的变化规律,求取最大下落速度,在对锚和锚链进行受力分析的基础上,推导出锚下落运动微分方程,并给出定解条件。通过模拟计算,直观显示锚下落速度的变化规律。进一步分析表明,锚机链轮的惯性阻力、锚入水冲击力及锚与锚链在水中的附加惯性阻力等仅延长锚到达最大速度的时间,对最大下落速度值的影响极小。锚的最大下落速度主要与锚和锚链的质量、二者在水中的阻力及锚链与锚链筒之间的摩擦阻力有关。
航海技术; 锚泊; 自由下落; 变质量; 数学模型
YUYang1,FANGJiasheng1,JIANGHaibo1, 2
Abstract: In order to know the variation and the maximum value of the dropping speed, the differential equation reflecting the anchor movement is built, and the definite conditions is defined based on the force analysis of the anchor and the chain. The anchor dropping is simulated based on the differential equation. The analysis reveals that the inertial resistance of chain grub wheel, water impact force and the additional inertial resistance of anchor and chain decrease the acceleration but have little effect on the maximum value of the dropping speed. The maximum dropping speed is primarily affected by the weights of the anchor and the chain, the resistances of those in water, the frictional resistance between the chain and the hawse pipe and the force from brake band, if exerted.
Keywords: navigation technology; anchoring; dropping by its weight; variable mass; mathematical model
船舶采用自由下落法抛锚时,锚的下落速度关系到锚泊安全。船舶在锚地抛锚时,通常根据锚地水深的不同采用自由下落式抛锚和锚机送锚式抛锚2种方法,其中:自由下落式抛锚又称重力式抛锚,适用于一般水深的锚地,锚触底时间短,易于控制船位;锚机送锚式抛锚适用于深水锚地,锚触底速度小,但操作复杂,用时较长,落锚点不易控制。这2种抛锚方法虽然在操作上有所差别,但都要控制锚的下落速度以保证安全。
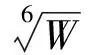
鉴于上述情况,对锚自由下落时与锚链的受力情况进行分析,给出变质量、变加速度的锚下落运动模型,以便揭示锚下落运动规律,并作为开展相关研究的基础。
1 变质量质点运动方程一般表达式
一个质点在运动过程中连续地减少或增加质量时,由动量定理可推导出变质量质点运动矢量方程[7]为
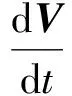
(1)
式(1)中:m为变质量质点质量,m=m(t),即质量为时间t的单值连续函数;V为质点运动速度;F为质点所受外力的合力;Vr为微质量在加入或离开质点时与质点的相对速度;dm为加入或放出的微质量。
以上物理量均采用标准国际单位。当dm/dt>0时,表示不断有质量加入;当dm/dt<0时,表示不断有质量放出。
2 锚自由下落运动方程
在锚下落过程中,不断有锚链从锚链舱加入到锚与锚链的运动中来。在t时刻,运动系统包括锚的质量和锚链的质量,加入运动的微质量是单位时间内锚链舱中从静止状态到运动状态的那一段锚链的质量。因此,系统的质量可写成
m(t)=ma+mc(t)
(2)
式(2)中:ma为锚的质量(固定值,不随时间变化);mc为锚链的质量,是时间t的函数。
图1为锚设备布置示意,其中锚已备妥,悬挂在水面之上。
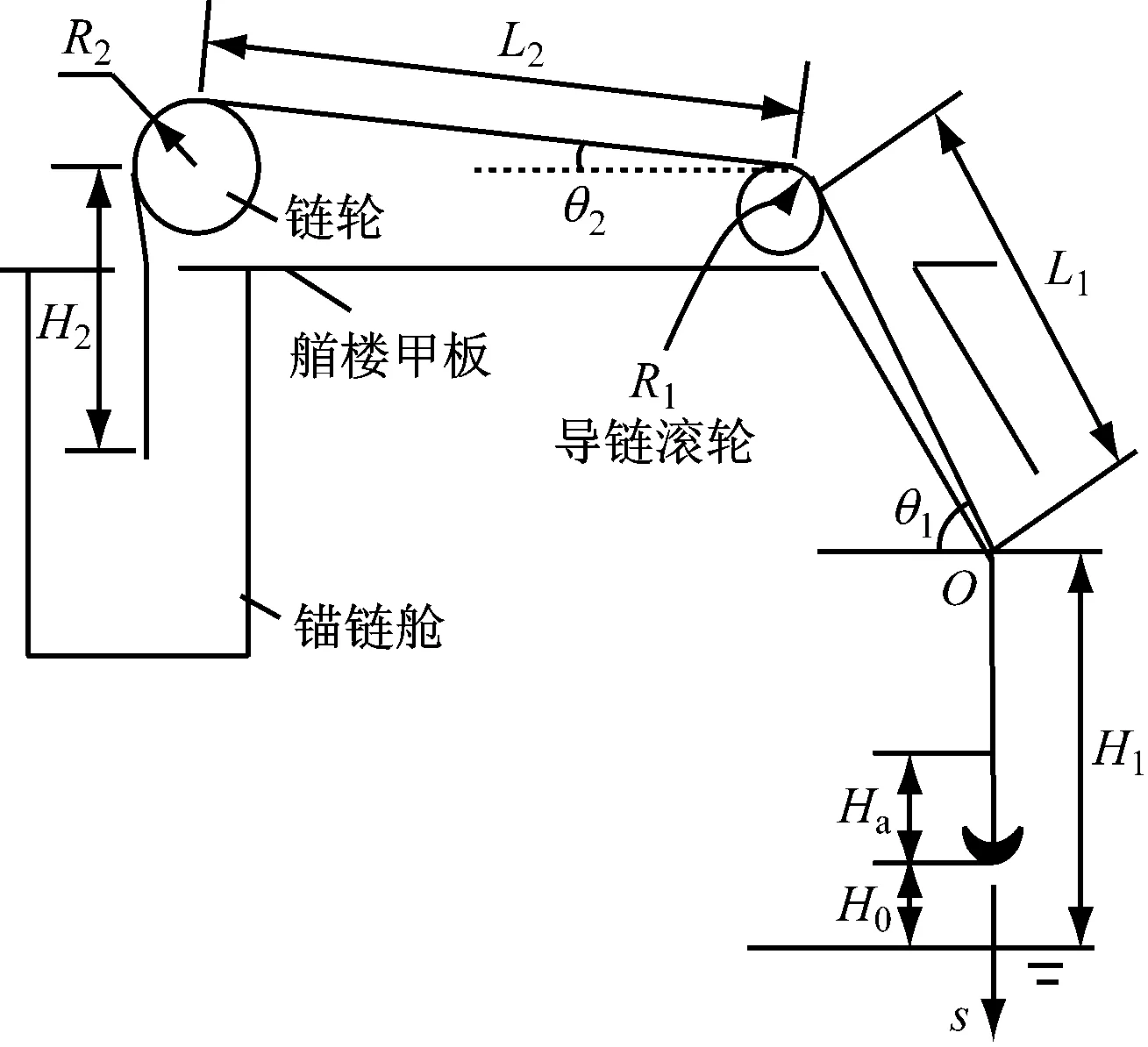
图1 锚设备布置示意
现取曲线坐标s,与锚链线重合,其原点O设在舷外垂直段锚链上的端点处。运动中的锚链长度S(t)为
S(t)≈s(t)+L1+L2+0.5π(R1+R2)+H2
(3)
式(3)中:s(t)为锚卸扣至锚链筒下端口(即坐标原点)的垂直距离;H2为锚机链轮至锚链舱的垂直段锚链长度,随锚链的不断放出而逐渐增大,但考虑到锚链舱直径较大,其增加量比锚链的放出长度小很多,故在放出锚链不多的情况下假定H2为常量。
运动部分的锚链质量可表示为
mc(t)=γS(t)
(4)
式(4)中:γ为单位长度锚链质量。
由式(2)~式(4)可得
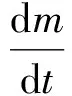
(5)
锚链舱内加入运动的微质量锚链在运动前的速度为0,运动后的速度为v,因此加入运动时的相对速度为-v,即vr=-v。将其与式(2)~式(5)一同代入到式(1)中,可得锚下落运动方程为

(6)
现在问题的关键是对锚和锚链系统进行受力分析,给出合外力∑F的具体表达式。
3 锚与锚链受力分析
船舶抛锚过程中锚与锚链所受的外力包括:锚与锚链的重力,锚入水时所受的冲击力,锚与锚链在水中所受的浮力、阻力和附加惯性阻力,锚链与锚链筒、锚链管的摩擦力,锚机链轮与导链滚轮的惯性阻力,锚机链轮、导链滚轮与转轴之间的摩擦阻力及刹车阻力等。在这些外力中,锚链与锚链管的摩擦阻力,锚机链轮、导链滚轮与转轴的摩擦阻力及导链滚轮的惯性阻力忽略不计。
3.1锚入水所受冲击力
锚入水时的冲击力F3的计算较为困难,这里采用卡门模型[8]近似计算为
F3=c3ρwv2AH1-Ha≤s (7) 式(7)中:ρw为水的密度;A为锚入水时锚体的水平投影面积;Ha为锚体高度;Δs为锚从击水开始至结束的垂直距离;c3为无因次系数,根据文献[8]可推得其值为 (8) 式(8)中:ρs为钢的密度;α为锚入水时锚的底升角,亦即锚冠底面与水平面的夹角。 3.2锚与锚链重力(含浮力) 锚与锚链的重力在入水前为其空气中的重力;入水后,其水上部分为空气中的重力,水下部分为水中的重力。 1) 锚的重力F1为 (9) 2) 锚链的重力F2为 (10) 式(10)中:Hd为锚链筒下端口至锚机链轮轴心的垂直高度。 Hd≈L1sinθ1+L2sinθ2+R1-R2 (11) 3.3锚与锚链在水中的阻力 锚与锚链在水中的阻力一般假定与运动速度的平方成正比,分别表示为 (12) (13) 式(12)和式(13)中:d为锚链直径,m;c4和c5分别为锚与锚链水阻力无因次系数,c4=0.6,c5=0.2。 3.4锚与锚链在水中的附加惯性阻力 锚与锚链在水中作加速运动时会带动周围水体一起加速运动,即锚与锚链要对周围水体施加一个作用力来推动该水体作加速运动。根据理论力学中的达朗贝尔原理,水体对锚与锚链的反作用力可用惯性阻力的形式计入外力系中。锚的附加惯性阻力F6及锚链的附加惯性阻力F7分别表示为 (14) (15) 式(14)和式(15)中:maa和mca分别为锚与锚链的附加质量;maa需通过试验确定;mca由式(36)给出。 3.5锚链与锚链筒的摩擦力 锚链与锚链筒的摩擦力记为F8,可表示为 F8=fcT (16) 式(16)中:fc为锚链与锚链筒摩擦阻力系数,比钢与钢的摩擦因数大一些,具体数值需通过试验确定;T为锚链筒舷外孔处锚链张力,可根据舷外垂直段锚链(s≥0)及锚的运动方程来建立T与其他变量间的关系。该方程也是一个变质量物体运动方程。由于从s=0点上方加入的锚链微质量速度与垂直段锚链速度相同(即vr=0),因此可推得 (17) 3.6锚机链轮的惯性阻力 锚在加速下落过程中,锚机链轮以相应的角加速度转动而产生惯性阻力,根据达朗贝尔原理,将该阻力F9计入外力系中,有 (18) 式(18)中:ε为链轮角加速度;I为锚机链轮包括与链轮固定在一起的刹车带轮的转动惯量。 3.7锚机刹车力 锚下落过程中锚机刹车带施加到锚链上的阻力记为F10,随刹车手轮的旋紧而逐渐增大。 备锚阶段,刹车带为刹紧状态;抛锚时,刹车带在逐渐旋松过程中虽然尚未完全松开,但只要刹车力小于锚及部分锚链的重力,锚就开始下落。锚下落的临界刹车力为F0≈(1-fc)[Ma+γ(s+Hd-H2)]g,其中fc为锚链与锚链筒之间的静摩擦因数。随着刹车带继续旋松,刹车力迅速减小。假定刹车力的下降规律为F10=F0e-5t,即 F10=(1-fc)[Ma+γ(s+Hd-H2)]ge-5t (19) 锚开始移动后,fc取动摩擦因数。 至此,锚与锚链运动系统所受的主要外力均已得到,合外力可表示为 ∑F=(F1+F2)-(F3+F4+F5+F6+F7+F8+F9+F10) (20) 联立式(6)~式(15)及式(17)~式(20),得到锚下落运动方程为 (21) 式(21)中:M(s),W(s)和Γ(s)根据锚下落阶段的不同而有不同写法。 1) 锚冠入水之前(s (22) W(s)=(1-fc)[ma+γ(s+Hd-H2)]g-F10 (23) Γ(s)=γ (24) 2) 锚击水阶段(H1-Ha≤s Γ(s)=(1-fc)c3ρwA+γ (25) M(s)和W(s)仍为式(22)及式(23)。 3) 锚击水阶段结束、锚链入水之前(H1-Ha+Δs≤s (26) W(s)=(1-fc)[0.87ma+γ(s+Hd-H2)]g-F10 (27) Γ(s)=(1-fc)c4ρwA+γ (28) 4) 锚链入水后(s≥H1) (29) W(s)=(1-fc) [0.87ma+γ(H1+Hd-H2)+ 0.87γ(s-H1)]g-F10 (30) Γ(s)=(1-fc)ρw[c4A+c5d(s-H1)]+γ (31) 再补充一个方程 (32) 及初始条件 (33) 式(33)中:H0为备锚后锚冠至水面的距离。式(21)~式(33)就是锚下落运动的微分方程和定解条件。采用数值方法求解上述方程较为方便。将式(21)和式(32)中的微分用差分代替,则有 (34) si+1=si+0.5(vi+1+vi)Δt (35) 式(22)~式(31)中的S和s换成Si和si即可,与式(34)及式(35)组成差分求解格式,其中Δt为时间步长,自行设定。 具体计算步骤: (1) 利用初始条件式(33),将t=0时刻的s1=H1-Ha-H0代入到式(22)和式(23)中,求出M(s1)和W(s1); (2) 将其与Γ(s1)=r和v1=0一起代入到式(34)中求出v2,然后用式(35)求出s2; (3) 得到v2和s2后,重复上述步骤求出v3和s3,以此类推,第1阶段的计算结果作为第2阶段计算的初始条件,直到第4阶段即可将锚下落过程中的速度和位置及随时间变化的情况计算出来。 此外,在第4阶段,随着锚链入水长度越来越大,锚链的附加质量mca也越来越大,可将其表示为 (36) 式(36)中:c7为无因次系数;3.6d为有挡链环宽度。文献[9]给出c7=0.1。 为直观地了解数学模型,进行模拟计算,其中锚链与锚链筒的摩擦因数、锚在水中加速下落时的附加质量在算例中取近似值。 某船配备霍尔锚,单锚质量ma=6 000 kg,锚体高度Ha=3.285 m,锚头投影面积A=1.881 m2,配2级锚链,锚链直径d=0.068 m。锚机链轮半径R2=0.45 m,转动惯量I=270 kg·m2,导链滚轮半径R1=0.2 m。锚链筒长L1=4 m,与水平面夹角θ1=50°,筒体下端距水面高H1=8 m;导链滚轮与锚机链轮间距L2=3 m,θ2=15°。锚机链轮下方至锚链舱内悬垂锚链长度H2=4 m。备锚后,锚距水面高H0=1.5 m。假设锚的附加质量为锚排开同体积水的质量的1.6倍,即maa=1.6maρw/ρs;锚链与锚链筒静摩擦因数fc=0.25,动摩擦因数为0.2。在计算系数c3时,将霍尔锚锚冠至助抓突角的倾斜角α近似取为30°,则得c3=4.5。锚击水进程取Δs=1.1 m。海水密度为1 025 kg/m3,钢密度为7 850 kg/m3。时间步长Δt=0.02 s。当|vi+1-vi|/vi<0.001时,计算停止。计算出的锚下落速度与位置的关系见图2。 图2 锚下落速度与其位置关系 从图2中可看出,锚下落的基本规律为:从备锚位置到入水前的速度随下落距离的增大而逐渐增大,入水时受击水反作用力的影响而又渐渐减小;击水阶段之后,速度持续增大,直至趋于稳定值。NAKAYAMA[10]所进行的实船投锚试验结果表明,质量为6.84 t的霍尔锚从水面之上3.4 m处抛下,落到水下17 m时的速度是6.8 m/s。算例中锚的质量及抛锚高度虽与其存在差别,但结果大体上吻合。 运用变质量质点运动方程建立锚下落运动数学模型,推导出变质量、变加速度的锚运动微分方程,并给出定解条件。从模拟算例结果看,该模型描述的锚下落运动规律基本上符合实际情况。锚机链轮的惯性阻力、锚入水冲击力及锚与锚链在水中的附加惯性阻力影响着锚下落速度变化过程,使锚达到最大速度的时间延长,但对最大下落速度值的影响极小。锚的最大下落速度取决于锚与锚链的质量、二者在水中的阻力及锚链与锚链筒之间的摩擦力和刹车力等。在模拟计算中,锚链与锚链筒的摩擦因数、锚入水冲击力及锚在水中的附加质量等是估算的,还需要试验测定和验证。下一步将开展相关研究以完善该模型,并通过实船抛锚试验来验证。 [1] 龚少军,尤庆华. 船舶深水抛锚方法分析[J]. 中国航海,2008,31(2): 193-196. [2] 王迎松. 锚泊贯入量的研究[D]. 大连:大连海事大学,2014. [3] 龚少军,尤庆华. 船舶抛锚作业锚机刹车最小临界水深计算[J]. 中国航海,2009, 32(4): 69-71. [4] 本田启之辅. 操船通论[M]. 东京:成山堂书店,2008:119-120. [5] 姚化利. 自由抛锚控制技术研究方向的看法[J]. 船舶,2009(5): 44-46. [6] Japan P & I Club. Preventing an Anchor from Dragging[J]. P & I Loss Prevention Bulletin, 2013, 25: 1-32. [7] 程勉. 变质量力学基础[M]. 北京:人民教育出版社,1982:1-7. [8] ZHAO L Y. Analytical Solution of the Problem of Two Dimensional Wedge Entering Water[D]. Harbin: Harbin Engineering University, 2012. [9] GOBAT J I. The Dynamics of Geometrically Compliant Mooring Systems[D]. Massachusetts Institute of Technology, 2000. [10] NAKAYAMA S, KIYOMIYA O. Depth of Penetration of Anchors into Seabottom Through Anchoring Tests[R]. Technical Note of the Port and Harbour Research Institute, Ministry of Transport, 1975. MathematicalModelofAnchorDroppingbyitsWeight (1.Navigation College, Dalian Maritime University, Dalian 116026, China; 2.Safety Management Department, China Shipping Passenger Liner Co., Ltd., Dalian 116003,China) U675.922 A 2016-04-11 国家自然科学基金(51379026) 于 洋(1963—),男,辽宁大连人,教授,博士,主要研究方向为船舶流体力学与航海技术。E-mail: ekship@aliyun.com 1000-4653(2016)02-0071-05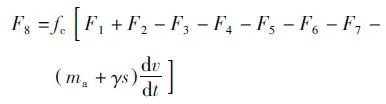
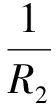
4 锚下落运动数学模型建立




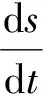
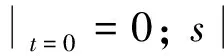
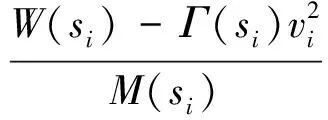

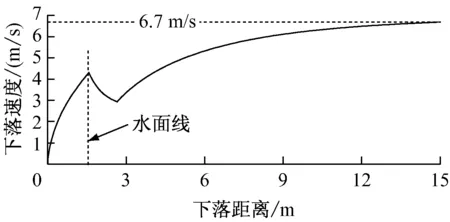
5 模拟算例
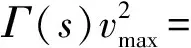
6 结束语

