去滑动均值趋势的De Wijs模型多重分形特征分析
赖佳境,万丽,2,熊绪沅
(1. 广州大学 数学与信息科学学院,广东 广州,510006; 2. 广州大学 数学与交叉科学广东普通高校重点实验室,广东 广州,510006)
去滑动均值趋势的De Wijs模型多重分形特征分析
赖佳境1,万丽1,2,熊绪沅1
(1. 广州大学 数学与信息科学学院,广东 广州,510006; 2. 广州大学 数学与交叉科学广东普通高校重点实验室,广东 广州,510006)
运用去滑动均值算法,探讨了De Wijs模型的多重分形特征。结果显示,趋势波动函数Fq(s)与尺度s具有较好幂律关系,Hurst指数h(q)与标度函数τ(q)都是随q变化的非线性函数,且随着富集参数d的增大,多重分形谱f(α)曲线跨度越大,指示多重分形特征越明显。这表明去滑动均值算法是识别De Wijs模型的多重分形特征及区分其分形强度的有效方法,可为进一步应用于实验数据的非线性特征分析提供理论指导。
去滑动均值算法; De Wijs模型; 多重分形; Hurst指数; 标度函数
分形是非线性理论的重要分支,是研究自然界和非线性系统中存在的不光滑与不规则的具有相似性且没有特征长度的形状和现象的科学,它广泛应用于生物医学、地质学、计算机科学等领域[1-3]。多重分形也称为多标度分形或多标度分形测度,可以用来描述具有无穷自相似层次结构系统的自相似、自仿射的特性,刻画动力学系统的长期演化和自相似行为[4]。一般使用多重分形的奇异强度 α对应的Hausdorf维数f(α)或者q阶矩广义维参数Dq来量化多重分形的统计属性。目前,主要方法有R/S分析法、统计矩法、多重分形去趋势波动分析、熵分析、小波模极大值分析等[5-7]。这些方法各有其优缺点,分别适合不同特征数据研究。
近年来,基于去趋势波动分析的系列方法在描述多重分形特征方面有广泛的应用。利用滑动均值作为趋势,Alessio提出了去趋势滑动均值算法(DMA)用于估计时间序列的Hurst值,由于DMA可以在无任何假设条件下处理非平稳信号的长相关性,可以较好地控制波动函数和标度之间的幂律关系,DMA已广泛地应用于实际时间序列中。然而,仅用一个Hurst值很难描述时间序列的多标度和复杂性,因此,Gu[8]和 Zhou[9]将去趋势滑动均值算法(DMA)推广到多重分形上,发现多重分形去趋势滑动均值算法(MFDMA)在对数据的处理上比多重分形去趋势波动分析(MF-DFA)具有更加精确的估计,因为MFD-FA会由于多项式拟合在分割点处的不连续性而引入新的波动,从而导致标度指数的估计错误。而多重分形去趋势滑动均值算法(MFDMA)是在去趋势滑动均值(DMA)的基础上提出来的,它是通过计算每一个滑动窗口的平均值来代替MF-DFA的多项式拟合,使MFDMA能够更加精确地估计序列的Hurst指数,显示出更好的幂律关系以及更加精确的多重分形标度指数和多重分形谱[10-12]。
本文将以De Wijs模型为研究对象,运用多重分形去趋势滑动均值算法研究不同聚集参数的多重分形特征,验证 MFDMA方法对分形强度识别的有效性,为进一步应用于实验数据的非线性特征研究提供新的方法。
1 多重分形去趋势滑动均值分析
对于非平稳的时间序列x(t),t = 1,2,3,…,N,N代表时间序列的长度[13]。
第1步,构造一个由原始时间序列产生的累积和

第2步,在滑动窗口的基础上计算时间序列累积和式(1)的滑动均值函数


第3步,通过累积和y(t)减去式(3)来消除序列的趋势,然后得到残差序列

第6步,根据不同的划分长度s,有波动函数

其中,h(q)就是所指的广义Hurst指数。
第7步,计算单个广义Hurst指数h(q),s取某定值,q取不同值,重复上述步骤,并对式(5)取对数,拟合曲线斜率,由

得到广义h(q)值,其中k为常数。
第8步,求多重分形奇异指数α以及多重分形光谱函数f(α)。

根据勒让德变化,得到多重分形奇异指数α以及多重分形光谱函数f(α):

然后把式(7)代入式(8),可得

由式(9)可以绘制多重分形光谱,即重分形奇异指数α以及多重分形光谱函数f(α)的关系图。若f(α)是固定值,则原始时间序列是一个单分形; 若f(α)是随α变化的曲线,则原始时间序列是一个多重分形的情况[14-16]。
2 实证分析
2.1De Wijs模型(矿化富集模型)

图1是通过Matlab编程产生的De Wijs模型序列,其中富集指数d从0.1到0.9取值。由图1可知,随着参数d取值的增大,数据的差值逐渐增大,序列的波动性越来越强[17]。

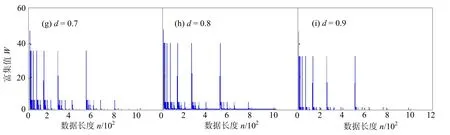
图1 不同参数的De Wijs模型序列
2.2计算结果与分析
根据式(1)~(6),计算波动函数Fq(s),然后绘制其双对数坐标lnFq(s)—ln(s),结果见图2。其中选取-10 ≤ q ≤ 10,步长1。为了更准确地估计标度指数h(q),区间长度s取值需适中,因为其取值太小没有实际意义,若过大,则分割的区间数Ns太少。本文取5 ≤ s ≤ N/4,这样既排除了小尺度带来的偏差,也避免了大尺度可能存在的斜率变化所带来的影响。
图2为q = -10,-1 ,…,1,2时,Fq(s)与s的双对数函数图,最下边的曲线为q = -10,最上的曲线为q = 10,按照间隔为1往上取值,共有21条曲线。
根据式(7)~(8),计算出Hurst指数h(q)和标度函数τ(q),结果见图3和图4。

图2 不同参数的lns—lnFq(s)曲线

图3 不同参数的q—h(q)曲线
图3为广义Hurst指数h(q)随q的变化曲线,它能反映序列是否存在多重分形行为。当变化曲线为水平直线时,即广义Hurst指数h(q)与q无关,表明{xi}是单分形,否则为多重分形。从图3中不同参数的q—h(q)图像可知,当q从-10到10变化时,h(q)不为常数,而是随着q的增大而减小,说明这个序列存在多重分形特征。

图4 不同参数的q—τ(q)曲线
图4是不同参数d下的q—τ(q)曲线。从图4可知,τ(q)和q之间都存在非线性关系,当d = 0.1时,q—τ(q)图像趋于一条直线,也就是说其多重分形特征很弱,已经将近趋于一个单分形序列了,但是随着参数d的不断增大,非线性特征越来越明显,可以说它的多重分形特征越来越明显。
固定参数d,根据Matlab环境下输出的数据,统计出不同参数d下Hurst指数h(q)的最小值h(q)min和最大值h(q)max,以及标度函数τ(q)的最小值τ(q)min和最大值τ(q)max,再分别计算h(q)的最大值与最小值之差Δh(q),以及τ(q)的最大值与最小值之差Δτ(q),结果见表1。

表1 不同参数下的Hurst指数h(q)与标度函数τ(q)的值
表1显示了不同参数下的Hurst指数与标度函数τ(q)计算结果。由表 1可知,随着参数d的不断增大,h(q)的极差 Δh(q)也越来越大,说明它的多重分形特征也越来越明显。当τ(q)和q之间存在线性关系时,序列是一个单分形的序列; 当 τ(q)和 q之间存在非线性关系时,序列是一个多重分形的序列,而且越强的非线性,它的多重分形特征就越强。因此,参数越大的标度函数 τ(q)的极差越大,曲线更趋于非线性,而参数小的则趋于线性关系。也就是说,随着参数的不断增大,标度函数并不具有线性特征,它的多重分形特征越明显。
由式(9)可得奇异性指数α与多重分形光谱f(α),并得到奇异性指数α与多重分形光谱f(α)两者之间的关系,结果见图5。由图5可知,f(α)随着奇异指数α的变化而不断变化。若多重分形谱α—f(α)是一条曲线,说明不同的奇异指数对应的分形谱不同,即奇异性程度不同的部分有不同的分形维数,所以序列为多重分形。而且由于参数d的不同取值,造成其多重分形谱的强度各不相同,奇异指数随d的增大而增大,此时,多重分形强度也越大。较大的多重分形谱宽度和较好的对称性说明,实验序列具有较强的多重分形性。

图5 不同参数的多重分形谱α—f(α)曲线
为了进一步验证实验结果,统计出Matlab环境下输出的奇异性指数α的最大值αmax和最小值 αmin,以及多重分形强度 f(α)的最大值 f(α)max和最小值 f(α)min,并计算α 与f(α)的最大值和最小值之间的极差Δα与Δf(α),结果见表2。
由表 2可知,随着参数 d的不断增大,奇异性指数α的最小值不断减小,而α的最大值反而不断增大,这样就使多重分形谱的宽度Δα随着参数d的不断增大而增大,而且它的多重分形强度Δf(α)也越来越大。由图5和表2可知,随着参数d的不断增大,它对应的多重分形强度也越来越大。

表2 不同参数的α与 f(α)值
3 结论
De Wijs模型是模拟成矿元素或矿物富集分布的经典模型,本文运用去滑动均值算法对不同富集参数的De Wijs模型的多重分形特征进行了分析,研究发现:在去除滑动均值后,其趋势波动函数Fq(s)与尺度s之间具有较好的幂律关系,且随着富集参数d的增大,广义Hurst指数h(q)和标度函数τ(q)均是随q的变化越明显,多重谱曲线f(α)跨度也越大,指示多重分形特征越明显。这说明去滑动均值算法可以有效识别De Wijs模型的多重分形特征以及区分其分形强度,可为进一步应用于实验数据的非线性特征分析及提供理论指导。
[1] 谢和平,薛秀谦. 分形应用的数学基础与方法[M]. 北京:科学出版社,1997.
[2] Ihlen E A F. Introduction to multifractal detrended fluctuation analysis in matlab [J]. Front Physion,2012,3:1-18.
[3] 万丽,邓小成,王庆飞,等. MF-DFA方法与成矿元素分布特征——以大尹格庄金矿为例[J]. 中国矿业大学学报,2012,41(1):133-139.
[4] 朱华,姬翠翠. 分形理论及其应用[M]. 北京:科学出版社,2011:207-221.
[5] Ihlen E A F. Multifractal analyses of response time series:a comparative study [J]. Psy Soc,2013,45:928-945.
[6] 燕爱玲. 河川径流时间序列的分形特征研究[D]. 西安:西安理工大学,2007.
[7] Murguia J S,Rosu H C. Multifractal analyes of row sum signals of elementary cellular automata [J]. Physica A,2012,391:3 638-3 649.
[8] Gu G F,Zhou W X. Detrending moving average algorithm for multifractals [J]. Phys Rev,2010,82(1):1 859-1 860.
[9] Zhou W J,Dang Y G,Gu R B. Efficiency and multifractality analysis of CSI 300 based on multifractal detrending moving average [J]. Physica A,2013,392:1 429-1 438.
[10] Wang Y D. Wu C F. Efficiency of crude oil futures markets:new evidence from multifractal detrending moving average analysis [J]. Comput Econ,2013,42:393-414.
[11] 袁晓辉,齐习文,田昊,等. 基于改进型MF-DFA的月径流序列多重分形分析[J]. 水力发电,2011(9):21-24.
[12] 熊杰,陈绍宽,韦伟,等. 基于多重分形去趋势波动分析法的交通流多重分形无标度区间自动识别方法[J]. 物理学报,2014,63(20):200504-1-8.
[13] 曹广喜,史安娜. 上海股市收益的多重分形分析——滑动窗 MFDFA方法的应用[J]. 数理统计与管理,2007,26:875-880.
[14] Wang Y D,Wu C F,Pan Z Y. Multifractal detrending moving average analysis on the US dollar [J]. Physica A,2011,390:3 512-3 523.
[15] Shi W,Zou R B,Wang F A,et al. New image segmentation method based on multifractal detrended moving average analysis [J]. Physica A,2015,395:197-205.
[16] 林近山,陈前. 基于多重分形去趋势波动分析的齿轮箱故障特征提取方法[J]. 振动与冲击,2013,32(2):97-101.
[17] 杨光华,谢小良. 基于加权超网络的区域物流网络模型及特征分析[J]. 湖南文理学院学报(自然科学版),2008,20(3):53-57.
(责任编校:刘刚毅)
Multifractality analysis of De Wijs model based on multifractal detrending moving average analysis
Lai Jiajing1,Wan Li1,2,Xiong Xuyuan1
(1. School of Mathematics and Information Sciences,Guangzhou University,Guangzhou 510006,China; 2. Interdisciplinary Sciences of Guangdong Higher Education Institutes,Guangzhou University,Guangzhou 510006,China)
Multifractal detrending moving average analysis(MFDMA)is used to study the multifractal characteristics of the De Wijs model and identify the degree of enrichment d. The results show that fluctuation function Fq(s)and window size s have a better scaling law after detrending moving average (DMA). At the same time,Hurst exponent h(q)and scaling exponent τ(q)are non-linear function along with the change of q-order. As the increase of the degree of enrichment,the span of multifractal spectrum curve get more huge,showing the multifractal characteristics will be more clear. The results make us better to understand multifractal detrending moving average analysis is a good method to identify the multifractal characteristics of De Wijs model and distinct the multifractal strength,and further theoretical guidances can be provided to the nonlinear characteristic of the experimental data analysis.
MFDMA; De Wijs model; multifractal; Hurst exponent; scaling exponent
P 612
1672-6146(2016)02-0004-07
10.3969/j.issn.1672-6146.2016.02.002
赖佳境,345045301@qq.com。
2016-03-02
国家自然科学基金(41172295)。

