一种可变空气孔的光子晶体光纤

殷爱菡，陈 冬，付方博，熊 磊

（华东交通大学信息工程学院，南昌 330013）

光纤光缆技术与应用

一种可变空气孔的光子晶体光纤

殷爱菡，陈 冬，付方博，熊 磊

（华东交通大学信息工程学院，南昌 330013）

针对PCF（光子晶体光纤）很难同时获得平坦色散和低限制损耗的问题，设计了一种新的可变空气孔的PCF，通过改变包层中空气孔的大小来获得平坦色散和低限制损耗。采用FVFEM（全矢量有限元法）和APML（各向异性完美匹配层）的边界条件对该光纤的结构进行分析，在设定1.55μm处空气孔的有效折射率为1、石英的有效折射率为1.45的条件下进行了仿真计算，结果表明，该光纤在1.25～1.78μm波长范围内具有超平坦色散，并且色散值在0±0.68ps/（nm·km）范围内变化，其限制损耗低于10-3dB/m。

光子晶体光纤；色散；限制损耗；椭圆孔

0 引 言

自第一根PCF（光子晶体光纤）问世以来，PCF便凭借其无截止单模特性、超平坦色散、高双折射率以及可控的非线性等特性受到了广泛的关注［1-4］。PCF的纤芯和包层由空气孔组成，并且其结构参数可调，因此PCF的色散特性能够满足光纤通信、色散补偿和非线性光学等应用的要求［5-7］。最近，ISSA等人成功制作出了椭圆空气孔，证明了可以通过压缩圆形空气孔的PCF来获得椭圆空气孔的PCF，并能保证空气孔的大小一致［8］。基于此，本文设计了一种新型PCF，通过在光纤的纤芯区域引入椭圆形空气孔来获得高双折射率，同时，该PCF有着超平坦色散、低限制损耗以及最优的设计参数。采用FVFEM（全矢量有限元法）和APML（各向异性完美匹配层）的边界条件对该光纤的结构进行分析，并且在设定1.55μm处空气孔的有效折射率n0=1、石英的有效折射率为1.45的条件下进行实验分析。

1 理论方法

为了研究本文设计的PCF的模间双折射率、色散和有效模场面积，采用FVFEM和APML的边界条件求解麦克斯韦本征方程得到有效折射率neff，将APML作为边界条件，也能准确地求出色散等传输特性［9］。PCF的色散D计算公式如下：

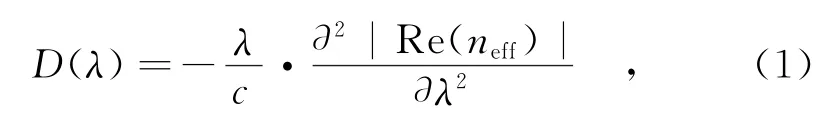
式中，c为真空中的光速，Re（neff）为neff的实部，λ为传输波长。光纤的总色散由材料色散Dm（也称几何色散）和波导色散Dw构成，即D（λ）≈Dw（λ）+Γ（λ）Dm（λ），式中，Γ为石英的限制因素，对于大部分折射率引导型PCF来说，Γ=1。Dm可直接由三阶迈耶尔公式求得，Dw则可由公式（1）求得。

PCF的有效模场面积Aeff与纤芯面积有关，其计算公式如下：

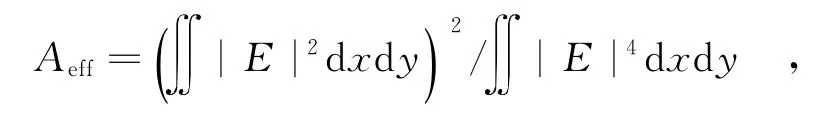
式中，E为介质的电场。低的Aeff可提供高密度的电场，这对于非线性效应来说是至关重要的。Aeff还与光斑尺寸有关：Aeff=π·ω2，式中，ω为光斑半径；此外，Aeff在限制损耗、微弯曲损耗、熔接损耗以及数值孔径方面有着重要的应用，Aeff越小，光纤的限制损耗、微弯曲损耗和熔接损耗也越小。

PCF的非线性系数γ的计算公式如下：

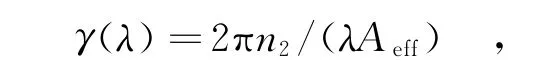
式中，n2为非线性系数的折射率，n2/Aeff表示非线性常数。

当光信号在纤芯区域传播时，由于空气孔层数有限，光信号会不可避免地从纤芯泄露到外层空气孔，从而产生损耗，称之为限制损耗。限制损耗Lc的计算公式如下：

式中，Im（neff）为neff的虚部，k0=2π/λ为自由空间的波数。

2 设计模型

本文设计的PCF的横截面如图1所示。其包层由6层圆形空气孔构成；在纤芯区域引入两个椭圆形空气孔来获得更高的双折射率。两个相邻圆形空气孔的间距为Λ，两个椭圆形空气孔的间距为Λ1，且有Λ1=Λ/2；dx和dy分别为椭圆的长轴和短轴，椭圆率η=dy/dx。包层中有3种大小不同的空气孔，我们设第1层空气孔的直径为d1，第2层空气孔的直径为d2，第3～6层空气孔的直径为d。空气孔的有效折射率n0=1，石英的有效折射率为1.45（在1.55μm波长处）。

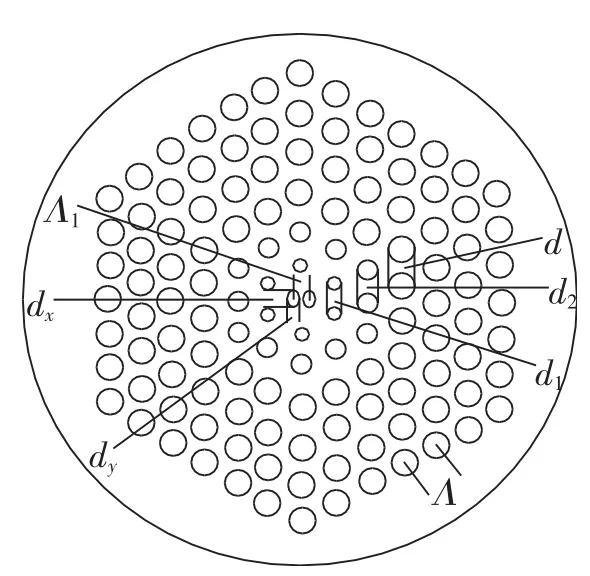
图1 PCF横截面示意图

3 仿真结果

3.1 优化特性

图2为本文设计的光纤在d1/Λ=0.3、d2/Λ= 0.6、d/Λ=0.75和Λ=0.6μm时的双折射率与波长的关系曲线。由图中可知，双折射率随波长的增大而增大，当η=0.4时，在1.55μm波长处双折射率达到了0.004 7；比较η=0.4、0.5和0.6这3种情形可知，η=0.4时可获得最高的双折射。

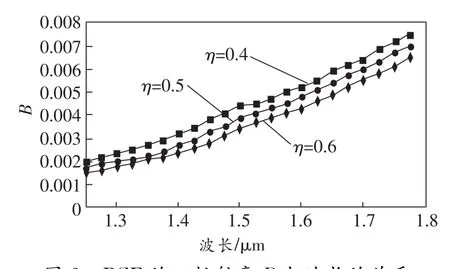
图2 PCF的双折射率B与波长的关系

图3、图4和图5分别给出了d1/Λ=0.3、d2/Λ=0.6、d/Λ=0.75、Λ=0.6μm和η=0.4时，PCF的限制损耗Lc、色散D和有效模场面积Aeff与波长的关系。由图可以看出，在1.25～1.78μm波长段（530 nm波段），Lc＜10-3dB/m（见图3）；且色散平坦，色散变化值为0±0.68 ps/（nm·km）（见图4）；在1.55μm波长处Aeff仅为2.2μm2（见图5），对应的γ＞45 W-1km-1。

图3 PCF的限制损耗Lc与波长的关系

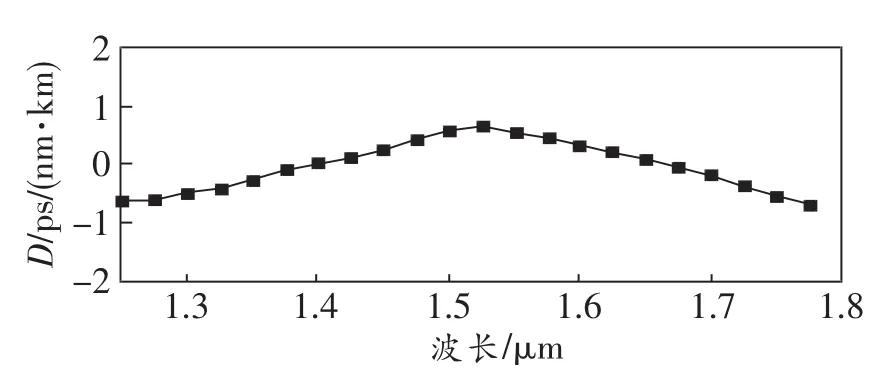
图4 PCF的色散D与波长的关系

图5 PCF的有效模场面积Aeff与波长的关系

3.2 PCF空气孔直径的影响

为了研究空气孔直径对PCF色散特性的影响，我们做了如下仿真：

（1）保持其他参数不变，将d1由之前的0.18μm变为0.20μm，得到如图6所示的色散曲线图。对比图4可以发现，色散曲线变化较大，因此我们得出以下结论：第1层空气孔的直径d1对色散平坦有着很大的影响。

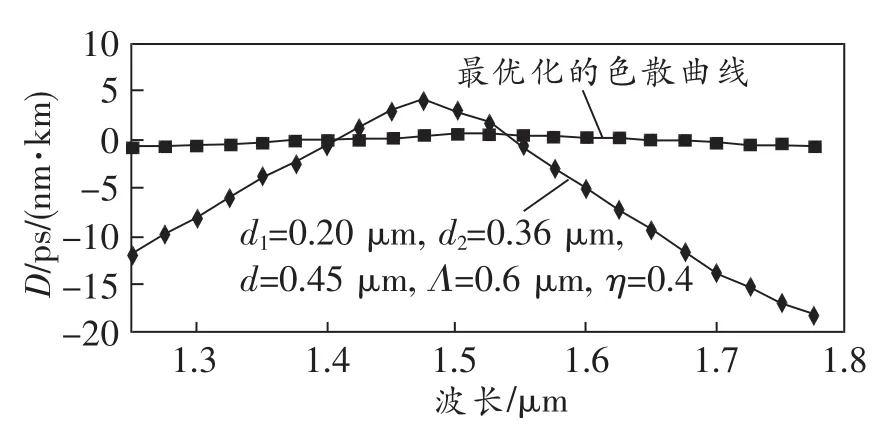
图6 改变d1后的色散曲线图

（2）保持其他参数不变，将d2由之前的0.36μm变为0.4μm，得到如图7所示的色散曲线图。对比图4、图6可以发现，虽然改变d2对色散也有一定的影响，但是色散变化不如改变d1时敏感，因此我们得出结论：第1层空气孔的直径对色散平坦的影响最大。

图7 改变d2后的色散曲线图

（3）保持其他参数不变，将d由之前的0.45μm变为0.5μm，得到如图8所示的色散曲线图。由图可见，改变d对色散几乎没有影响，表明色散对外层空气孔的变化不敏感。

图8 改变d后的色散曲线图

4 结束语

本文利用FVFEM和APML边界条件设计了一种纤芯为椭圆孔、包层为大小不同的空气孔的PCF。仿真结果表明：当d1/Λ=0.3、d2/Λ=0.6、d/Λ=0.75、Λ=0.6μm和η=0.4时，所设计的PCF 在1.25～1.78μm波段内色散变化只有0± 0.68 ps/（nm·km），高双折射率在1.55μm波长处达到了0.004 7，且限制损耗低于10-3dB/m。有效模场面积在1.55μm波长处只有2.2μm2，对应的非线性系数＞45 W-1km-1。这种新型PCF在光参数放大、全光信号处理和超连续谱产生等方面有着重要作用。

［1］ HAXHA S，ADEMGIL H.Novel design of photonic crystal fibres with low confinement losses，nearly zero ultra-flatted chromatic dispersion，negative chromatic dispersion and improved effective mode area［J］.Optics Communications，2008，281（2）：278-286.

［2］ KUNIMASA S，KOSHIBA M，HASEGAWA T，et al.Chromatic dispersion control in photonic crystal fibers：application to ultra-flattened dispersion［J］.Optics Express，2003，11（8）：843-852.

［3］ 陈静，谭晓玲.八角格子光子晶体光纤模式和色散特性研究［J］.光通信研究，2009，（2）：46-49.

［4］ VILLATORO J，MINKOVICH V P，ZUBIA J.Locally pressed photonic crystal fiber interferometer for multiparameter sensing［J］.Optics Letters，2014，39 （9）：2580-2583.

［5］ YAMAMOTO T，KUROKAWA K.160 Gbit/s OTDM signal transmission over 26 km photonic crystal fibre［J］.Electronics Letters，2008，44（18）：1080-1081.

［6］ 李政颖，孙文丰，李子墨，等.基于色散补偿光纤的高速光纤光栅解调方法［J］.物理学报，2015，64 （23）：234207-1-234207-4.

［7］ TRAVERS J C，TANI F，ABDOLVAND A，et al. Spatiotemporal Nonlinear Dynamics in Gas-Filled Photonic-Crystal Fibers［C］//Nonlinear Photonics. Washington，D.C.，US：OSA，2014：NW1A.1.

［8］ ISSA N A，VAN EIJKELENBORG M A，FELLEW M，et al.Fabrication and study of microstructured optical fibers with elliptical holes［J］.Optics Letters，2004，29（12）：1336-1338.

［9］ KAJLA A，GUPTA S，FALAH N，et al.Hexagonal Lattice Photonic Crystal Fiber with Low Confinement Loss and Low Chromatic Dispersion［J］.Journal of E-lectrical and Electronics Engineering，2014，9（1）：01-05.

A Vary Air Hole Photonic Crystal Fiber

YIN Ai-han，CHEN Dong，FU Fang-bo，XIONG Lei
（School of Information Engineering，East China Jiaotong University，Nanchang 330013，China）

A new Photonic Crystal Fiber（PCF）with flattened chromatic dispersion and low confinement losses is proposed by varying the size of air hole.By employing a Full Vector Finite-Element Method（FVFEM）and Anisotropic Perfectly Matched Layers（APML），the structure and optical properties of the proposed PCF are analyzed.The simulation is conducted under the conditions that the effective refractive index of air hole at 1.55μm is n0=1 and the effective refractive index of quartz is 1.45. The results show that the proposed PCF has ultra-flattened dispersion of 0±0.68 ps/（nm·km）from 1.25μm to 1.78μm wavelength range with confinement losses lower than 10-3dB/m across all the wavelength range.

PCF；dispersion；confinement losses；elliptical hole

TN818

A

1005-8788（2016）03-0026-03

10.13756/j.gtxyj.2016.03.009

2015-12-30

国家自然科学基金资助项目（61262079）

殷爱菡（1963-），女，江西南昌人。教授，博士，主要研究方向为光通信技术。

陈冬，硕士研究生。E-mail：ecjtu5102@126.com