道路放样中具有卵形曲线的缓和曲线计算方法研究
■刘国光
(广州南方测绘仪器有限公司广东广州510665)
道路放样中具有卵形曲线的缓和曲线计算方法研究
■刘国光
(广州南方测绘仪器有限公司广东广州510665)
在道路放样中,经常会遇到不完整缓和曲线-卵形曲线的测设,对于卵形曲线要素计算过程在相关教材讲述较少,本文通过补充完整缓和曲线的方法,以规则缓和曲线数学模型为基础,由特殊曲线到一般曲线进行数据推导,并结合实际卵形曲线实例进行模型的验证工作。
缓各曲线 卵形曲线 曲线要素
1 前言
卵形曲线是指用一条回旋线连接两个同向曲线的组合曲线。卵形曲线的大圆必须把小圆完全包含在内。若大圆半径无限大,即直线,其即属于基本型。卵形曲线的回旋线不是从起点开始的完整回旋线,而是只使用曲率从到这一段的不完整回旋线。
在高等级公路与市政道路的匝道路线设计中,经常会遇到这种类型的曲线。由于其复杂性,在测量教材中,主要针对缓和曲线的两种基本型:∞→R及R→∞,对卵形曲线缺少相应的描述。本文试图通过补充完整曲线的方法计算卵形曲线要素,最后用实例进行验证,编写工具软件进行算法验证。
2 卵形曲线要素及坐标要素的推导
在测量学材中,我们常见的两种缓和曲线形式为直线-缓和曲线-圆曲线-缓和曲线-直线形式,缓和曲线无非就两种基本型:半径从无穷大到R(从直线到圆)和从R到无穷大(从圆到直线),中线坐标计算公式如下,其中数学坐标系计算公式为:

测量坐标系坐标转换公式为:
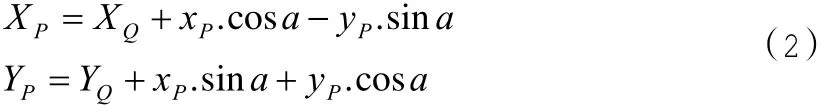
至此常规缓和曲线计算完毕。
在卵形曲线的计算中,经常会遇到圆曲线-缓和曲线-圆曲线的形式,即不完整缓和曲线,也是我们常说的卵形曲线,他是从一个半径R1过渡到另外一个半径R2,可分为从大半径到小半径,从小半径到大半径两种形式,两种形式均以向大半径补充完整为原则,
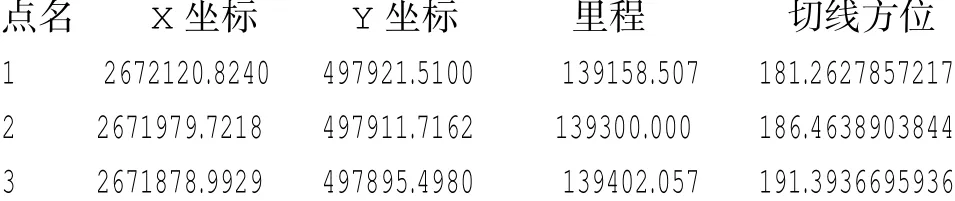
第一种情况:当R1→R2(R1 向R2端补充完整缓和曲线,设补充段缓曲长为LX,由于 LR=A2,即缓和曲线长与半径的乘积是一个常值,由此可知: 由此可得: 计算公式为:lI为任意点的缓曲长度,l0为完整级各曲线长度将lI和l0代入到(1)计算出XP、YP 坐标转换公式为: 其中: 将xP、yP和α代入(2)可计算出P点的坐标。 第二种情况:当R1→R2(R1>R2)时: 向R1端补充完整缓和曲线,设补充段缓曲长为LX,由于LR=A2,即缓和曲线长与半径的乘积是一个常值,由此可知: 由此可得: 计算公式为: 将lI和l0代入到(1)计算出xP、yP 坐标转换公式: 将xP、yP和α代入(2)可计算出P点的坐标。 实 例 : 第 一 缓 和 曲 线 起 点 ZH:K137+864.087(2673320.152,497509.476)起始方位角143°48′13.1″ ,第一缓和曲线长224.01,第一圆曲线弧长1070.41半径1800,第二缓和曲线长243.55,圆曲线弧长337.88半径1100,第三缓和曲线长227.27 由数据分析可知: 第一段曲线为完整的标准缓和曲线∞→R,第二段为圆曲线,第三段即为本文研究的缓和曲线,属于R1>R2类型,第四段也是圆曲线,第五段为也为标准的缓和曲线,为R→∞,本文主要研究第三段卵形曲线。 计算: 1、计算第一缓和曲线各点坐标,利用公式∞→R: 利用公式(1)计算各点在曲线坐标系中的坐标及利用坐标转换计算出在测量坐标系中的坐标,起算方位角为143°48′13.1″ 2、计算第一圆曲线中各点的坐标,圆曲线有两种计算方法,一种是利用综合曲线中缓和曲线的计算方法,一种是直接用圆曲线计算,注意两种曲线的起算方位与起算点具有差异性。 3、计算第二缓和曲线各点的坐标,利用R1→R2(R1>R2)中的公式 由于该缓和曲线是从大半径到小半径的变化,所以可利用公式(7)计算缓和曲线长,坐标转换中坐标原点的计算利用公式(8),再利用坐标转换计算公式计算,转换角利用公式(9)计算,最终计算坐标转换角175°20′59.56″ 坐标转换中坐标原点的计算: 将代入下式中 利用公式计算出各桩号在曲线坐标系中的弧长,再利用公式(1)计算出各点在曲线坐标系中的坐标,然后利用公式(2)计算出该桩号在测量坐标系中的坐标。 4、计算第二圆曲线各点的坐标,方法同二。 5、计算第三缓和曲线各点的坐标,方法同一。 本文卵形曲线相关算法经过编写工具软件GPSTOOL验证通过,软件结果表明,用补全法计算卵形曲线中线坐标回归完整曲线,然后利用一般的缓和曲线算法:从直线到圆和从圆到直径的两种缓和曲线形式进行计算,由特殊到一般,易于理解的同时,精度也能达到保证,易于编程实现,在实践验证中取得比较好的效果。 [1]张正辉,李海鹏,何方海.卵形曲线的坐标计算 [J].交通标准化,2007,3(2):129-130. [2]张家平,崔旭光,赵德龙.卵形曲线测设与计算要点解析 [J].黑龙江工程学报,2008,22(3):29-31. [3]钟孝顺,聂让.测量学 [M].北京:人民交通出版社,2001. [4]吕会军 龙晓荣.关于卵形曲线的平面坐标计算探讨 [J].中国水运,2007,5(6): P2[文献码]B 1000-405X(2016)-5-304-2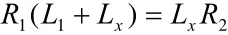








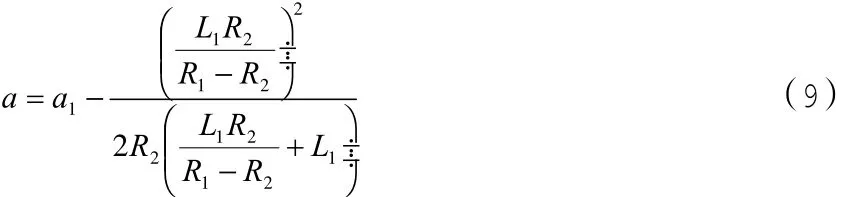
3 卵形曲线实例
4 结论
——奇妙的蛋

