基于时间序列分析的港口集装箱吞吐量预测分析

孔琳琳，刘　澜，许文秀，吴金卓*

(1.东北林业大学 工程技术学院 哈尔滨 150040；2.湖南工学院，湖南 衡阳 421002)



基于时间序列分析的港口集装箱吞吐量预测分析

孔琳琳1，刘澜2，许文秀1，吴金卓1*

(1.东北林业大学 工程技术学院 哈尔滨 150040；2.湖南工学院，湖南 衡阳 421002)

集装箱运输是现今国际运输的主要方式之一，长期监测港口集装箱吞吐量并对未来趋势进行相关的预测研究，对于港口基础设施建设、区域经济发展以及国家战略发展方面都有着非常深远的意义。本文针对影响港口集装箱吞吐量复杂性因素的非线性特点，以中国某港口2001年1月至2014年12月共14 a的集装箱吞吐量数据为例，利用统计分析软件R对该港口集装箱吞吐量数据进行时间序列分析，提出了一个合理的ARIMA模型来描述集装箱吞吐量的变化，并对模型进行检验优化，应用该模型预测十个月后的集装箱吞吐量数据。结果表明，利用统计分析软件R对港口集装箱吞吐量数据进行时间序列分析后得到的预测模型可以很好的描述港口集装箱吞吐量变化情况，据此可以为港口在不同时期制定最优措施提供参考。

集装箱吞吐量；时间序列分析；预测；模型

0　引　言

港口作为一个重要的交通枢纽，是各种交通工具的转换中心，大量货物聚集在此，不仅能促进当地经济的发展，而且也能拉动港口周边地区的工业发展，在一个国家的经济发展中发挥着至关重要的作用[1-2]。港口吞吐量这一指标就是反映一定时间内(一般为1 a)港口生产经营活动规模以及国家和地区经济发展状况的参考指标，对港口的建设和管理具有重大的影响。

港口吞吐量分为衡量旅客流动情况的旅客吞吐量和衡量货物流动情况的集装箱吞吐量两种。长期监测港口集装箱吞吐量并对未来趋势进行相关的预测研究，对于港口基础设施建设、区域经济发展以及国家战略发展方面都有着非常深远的意义[3-4]。翟希东[5]采用灰色理论模型和改进的神经网络模型结合的方法建立港口集装箱吞吐量预测模型，并以大连港集装箱吞吐量的实际发生数据为实验样本，验证了提出的集装箱吞吐量预测模型的有效性和实用性。黄维忠[6]为避免以往研究中吞吐量的预测值与实测值之间差距较大的情况，突破性地提出了一种动态预测方法对吞吐量进行预测，并以上海港为实例验证了此方法的可行性。江舰等[7]以大连港为例对集装箱吞吐量的影响因素以及其产生的经济影响进行计量分析，并建立了港口城市GDP与进出口商品总值对集装箱吞吐量影响的二元线性回归模型，从而很好地解释了其中的关系，也对国内其他港口城市起到了很好的借鉴意义。

市场经济、自然条件、国家政策等因素都是影响集装箱吞吐量的重要因素。由于这些因素具有极强的复杂性而不能用精确的语言来描述其作用机制，属于非线性系统问题，因此这些因素最终都会反馈在其时间序列上[8-9]。由此可见，对港口集装箱吞吐量建立时间序列进行分析不仅有利于了解集装箱吞吐量随季节变化的趋势，而且对其建模和预测有一定的指导意义。

本文采用统计分析软件R对国内某港口2001年1月～2014年12月的集装箱吞吐量进行时间序列分析，通过分析其季节性数据，确定吞吐量与季节变化之间的关系。通过建立ARIMA模型预测该港口十个月后的集装箱吞吐量数据，结合预测结果分析未来一段时间内港口吞吐量随季节变化的规律，对港口在不同时期制定最优措施提供参考。

1　研究方法

1.1时间序列分析

时间序列是指将一组数据按照时间推移的顺序进行排列。这些长时间的数据反映出来的整体向上或向下的趋势、在一年内随季节变化的情况、一段时间内呈现出的涨落相同的循环波动和无规律的随机波动4种变化情况构成了时间序列的4要素[10-12]。应用数理统计方法可以对具有时序性和相关性的时间序列进行分析，通过建模还可以预测事件未来的发展趋势及走向[13-15]。

本文利用R软件中的时间序列分析对某港口集装箱吞吐量进行分析。R软件是一个具有相关统计分析和作图功能的综合软件，其编程语言简单实用，作图功能强大，统计分析能力突出，可移植性强，同时还具有强大的数据存储和处理系统以及数组运算工具。其完整而连贯的统计分析工具非常适合用来做时间序列图来分析。根据R软件作出的时间序列图，分析数据的周期性变化，并对时间序列进行分解。对数据进行季节性修正，把季节性部分从原始时间序列中去除，可以得到仅包含趋势部分和不规则部分的季节性修正时间序列图。

1.2时间序列建模与预测

本文选用自回归积分滑动平均模型ARIMA(p，d，q)来建立港口集装箱吞吐量的时间序列模型，通过时间序列的差分，得到一个合适的ARIMA的模型，以此来预测2015年前十个月的港口集装箱吞吐量[16]。ARIMA(p，d，q)模型是为平稳的时间序列定义的，对于非平稳时间序列，需要进行差分，变为差分平稳序列后才能应用该模型。差分平稳序列可以用ARIMA(p，d，q)模型进行拟合。该模型的结构表示为：

(1)

对d阶齐次非平稳序列{Xt}而言，{▽dXt}是一个平稳序列，设其适合ARIMA(p,d,q)模型，即

φ(B)▽dXt=θ(B)εt。

(2)

或者

φ(B)(1-B)dXt=θ(B)εt。

(3)

其中

φ(B)=1-φ1B-φ2B2-…-φpBp。

(4)

为消除季节性影响和长期趋势影响，对该序列作一阶12步差分，检验序列是否平稳。如果时间序列平稳，就可以使用ARIMA(p,d,q)模型，其中d=1。

2　实例分析

2.1某港口集装箱吞吐量的时间序列分析

本文收集并整理了中国十大港口之一的某港口2001年1月至2014年12月集装箱吐吞量的数据，利用统计分析软件R对数据进行统计分析。首先，将数据读入到R中，绘制时间序列图，得到该港集装箱吞吐量时间序列图如图1所示。

由图1可知，该港口集装箱吞吐量时间序列总体呈现上升趋势，并且存在着一定的周期性变化。这个季节性时间序列由趋势部分、季节性部分和不规则部分3部分组成。

图1　某港口集装箱吞吐量时间序列图Fig.1 Time sequence chart of the handling capacity in a port

通过对时间序列的趋势的、季节性和不规则部分进行分析，得到了每年 1～12 月的季节性因素。季节性因素最大值在十月，最小值在二月，一、二、三、四、五、十二月集装箱吞吐量较少，标志着每年的峰值在十月，低谷在二月份。绘制出时间序列中估计的趋势、季节性和不规则的部分，时间序列的分解结果如图2所示。图2共分为4个部分，由上至下分别为：原始的时间序列图以及估计的趋势图、季节性图和不规则图。由图2可知，估计出的趋势部分从2001年开始逐年稳步上升，在2009年前后有下降的趋势，但随后又持续稳步上升。图2估计出的季节性部分图像稳定，说明该港口集装箱吞吐量存在一定的季节性规律，与前文分析相符。

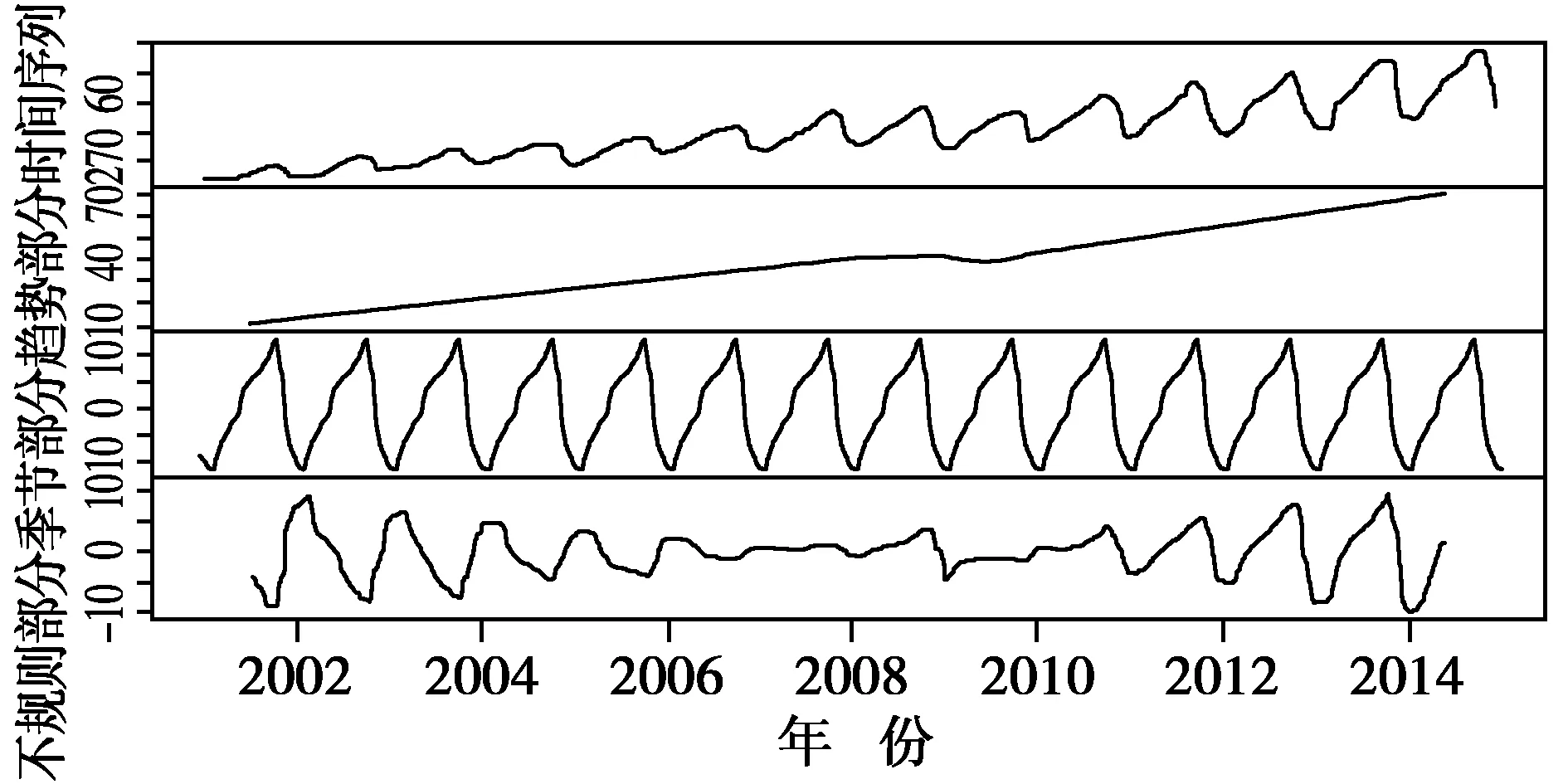
图2　时间序列的分解Fig.2 Decomposition of time sequence

对数据进行季节性修正，把季节性部分从原始时间序列中去除，得到仅包含趋势部分和不规则部分的季节性修正时间序列图如图3所示。由于剔除了季节性因素的影响，因此根据图3可知：2001年～2006年，该港口集装箱吞吐量呈现缓慢上升趋势，但吞吐量的增长情况并不稳定。2006年至2008年集装箱吞吐量增长速度呈直线上升，在2009年集装箱吞吐量下降，随后至2014年又呈现出缓慢上升的趋势，这主要是由于2008年全球金融危机全面爆发，沿海港口吞吐量下降所致[17]。

图3　季节性修正时间序列图Fig.3 Time sequence after seasonal adjustment

2.2港口集装箱吞吐量时间序列建模与预测

为消除季节性和长期趋势的影响，对时间序列作一阶12步差分，最终得到的时间序列如图4所示。差分后序列基本平稳。由于对原始时间序列数据做1阶差分获得了一个平稳时间序列，所以可以对时间序列使用ARIMA(p,d,q)模型，其中：p为自回归模型的阶数；d为差分阶数，由上述内容可知，本文中d=1；q为滑动平均模型的阶数。

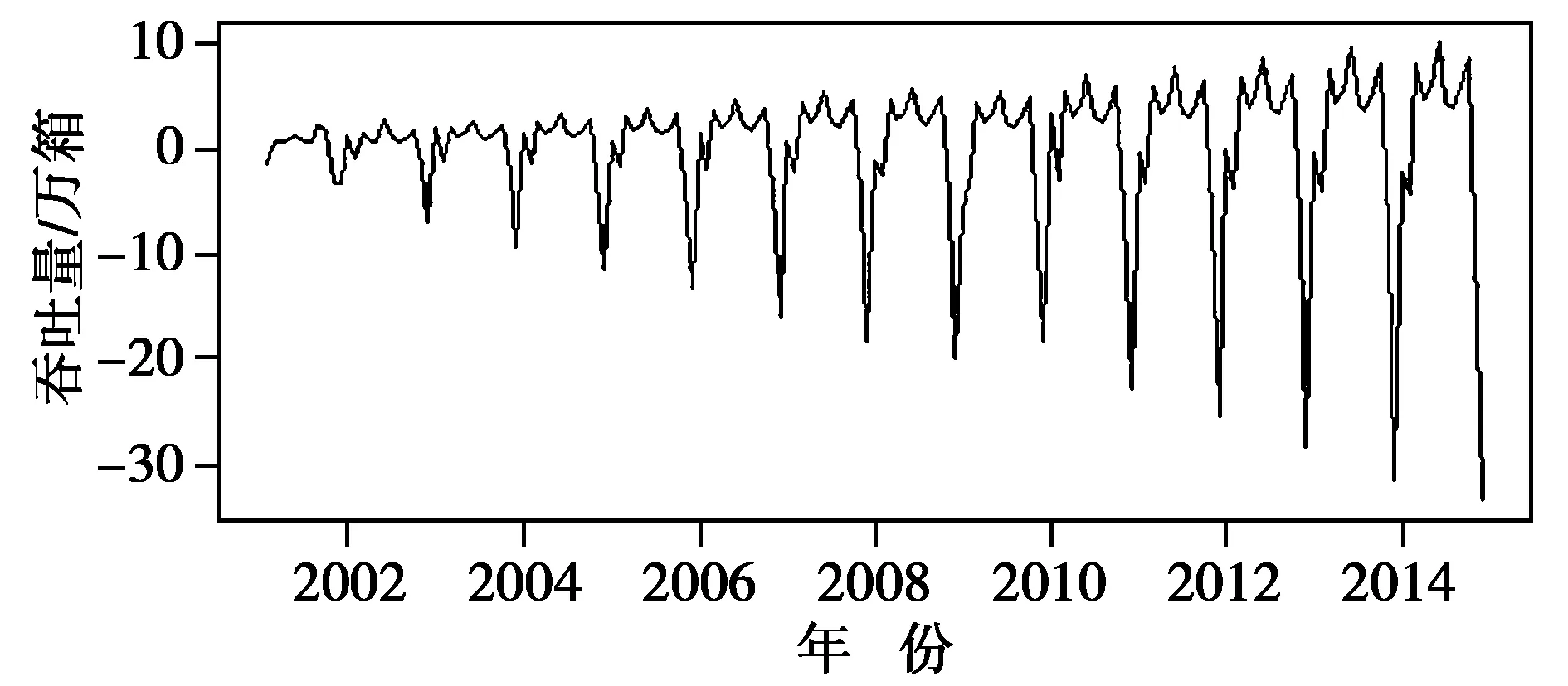
图4　差分后的时间序列图Fig.4 Time sequence after differential treatment

利用R软件的程辑包‘forecast’中的arima函数，自动对非平稳时间序列进行适当差分，分析求解出适合时间序列分析的模型。输入auto.arima()进行自动求解，最终输出结果说明该模型适合采用ARIMA(2,1,1)模型，通过分析得出模型为：

(1-1.1559B+0.4945B2)(1-B)Xt=(1+0.8978B)εt。

(5)

应用该模型来预测未来十个月该港口集装箱吞吐量的数据，得到结果见表1。表1反映了2015年1月～10月该港口集装箱吞吐量预测值，并显示了置信度为80%和95%时的置信区间。根据预测，2015年前十个月的吞吐量预计分别为：1月份44.087万箱，2月份45.301万箱，3月份53.267万箱，4月份61.875万箱，5月份67.885万箱，6月份70.575万箱，7月份70.713万箱，8月份69.542万箱，9月份68.120万箱，10月份67.056万箱。

表1　2015年1月～10月预测值(万箱)以及置信区间

预测值图像如图5所示，浅灰色阴影部分为80%预测区间，深灰色阴影部分为95%预测区间，阴影部分的线条表示预测值。

图5　港口集装箱吞吐量预测值图像Fig.5 Predicted handling capacity of the port

对该港口吞吐量数据使用ARIMA(2，1，1)模型后所产生的预测误差做自相关图如图6所示。由图6可以看出，相关图显示出之后1～20阶(lag1-20)中样本自相关值都没有超出置信边界，而且Ljung-Box检验p-value < 2.2e-16，所以得到的模型可以提供非常合适的预测。

图6　某港口集装箱吞吐量预测误差相关图Fig.6 Correlation diagram of prediction error

2015年1月～10月该港口集装箱吞吐量分别为46.721、47.014、56.335、60.982、68.452、73.146、75.178、70.015、69.574、68.739万箱，与预测结果44.087、45.301、53.267、61.875、67.885、70.575、70.713、69.542、68.120、67.056万箱相差甚微，在5%左右浮动，说明本模型对港口集装箱吞吐量可以提供较准确的预测。

3　结束语

本文分析了2001～2014年某港口集装箱吞吐量数据，通过时间序列分析，建立了集装箱吞吐量的ARIMA预测模型，并且预测分析了2015年该港口前十个月集装箱吞吐量，得到了以下结论：

(1)该港口集装箱吞吐量总体呈现上升趋势，2001～2003年这种趋势不明显，2003年以后随着中国加入世贸组织，上升趋势较为明显。2009年前后该港口集装箱吞吐量受金融危机的影响有下降趋势，一段时间后随着经济的回暖逐渐恢复正常，至2014年又呈现出上升趋势。

(2)该港口集装箱吞吐量呈现一定的季节性变化，季节性因素最大值在十月，最小值在二月，一、二、三、四、五、十二月集装箱吞吐量较少，标志着每年集装箱吞吐量的峰值在十月，低谷在二月份。

(3)利用R软件得到预测该港口2001年至2014年集装箱吞吐量的预测模型ARIMA(2，1，1)模型为(1-1.1559b+0.4945b2)(1-B)Xt=(1+0.8978B)εt，并对模型进行检验，结果证明得到的模型可以很好的描述港口集装箱吞吐量，从理论上证明了该港口集装箱吞吐量的增长趋势。

[1]叶峰，吴迎学.基于实现我国港口物流联盟的探索[J].森林工程，2009，25(5)：89-91.

[2]Huang A，Qiao H，Wang S.Forecasting container throughputs with domain knowledge[J].Procedia Computer Science，2014，31：648-655.

[3]Huang A，Lai K K，Qiao H，et.al.An interval knowledge based forecasting paradigm for container throughput prediction[J].Procedia Computer Science，2015，55：1381-1389.

[4]Chen S H，Chen J.Forecasting container throughputs at ports using genetic programming[J].Expert Systems with Applications，2010，37(3)：2054-2058.

[5]翟希东.港口集装箱吞吐量预测模型研究[D].大连：大连理工大学，2006.

[6]黄维忠.集装箱吞吐量的动态预测研究[J].上海海运学院学报，2001，22(1)：45-48.

[7]江舰，王海燕，杨赞.集装箱吞吐量及主要影响因素的计量经济分析[J].大连海事大学学报，2007，33(1)：83-86.

[8]陈涛焘，高琴.港口集装箱吞吐量影响因素研究[J].武汉理工大学学报，2008，30(6)：991-994.

[9]刘志杰，季令，叶玉玲，等.基于径向基神经网络的集装箱吞吐量的组合预测[J].同济大学学报，2007，35(6)：739-744.

[10]侯成琪，徐绪松.计量经济学方法之时间序列分析[J].技术经济，2010，29(8)：51-57.

[11]潘迪夫，刘辉，李燕飞.基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J].电网技术，2008，32(7)：82-86.

[12]罗芳琼，吴春梅.时间序列分析的理论与应用综述[J].柳州师专学报，2009，24(3)：113-117.

[13]韩忠明，陈妮，乐嘉锦，等.面向热点话题时间序列的有效聚类算法研究[J].计算机学报，2012，35(11)：2337-2347.

[14]钱爱玲，瞿彬彬，卢炎生，等.多时间序列关联规则分析的论坛舆情趋势预测[J].南京航空航天大学学报，2012，44(6)：904-910.

[15]杨娟丽，徐梅，王福林，等.基于BP神经网络的时间序列预测问题研究[J].数学的实践与认识，2013，43(4)：158-164.

[16]Aslanargun A，Mammadov M，Yazici B，et.al.Comparison of ARIMA，neural networks and hybrid models in time series：tourist arrival forecasting[J].Journal of Statistical Computation and Simulation，2006，77(1)：29-53.

[17]贾大山.金融危机对港口集装箱发展的影响[A].全球经济形势变化与我国集装箱运输发展对策研讨会论文集[C]，北京，2009：39-42.

Prediction of the Container Throughput in a PortBased on Time Sequence Analysis

Kong Linlin1，Liu Lan2，Xu Wenxiu1，Wu Jinzhuo1*

(1.College of Engineering and Technology，Northeast Forestry University，Harbin 150040；2.Hunan Institute of Technology，Hengyang 421002，Hunan Province)

Container transportation is one of the main modes of international transportation.Long-term monitoring port container throughput and predicting future trends are of importance to the port infrastructure construction，regional economic development and national strategy development.In this paper，aiming at the nonlinear characteristics of the factors affecting the complexity of port container throughput，the container throughput data in a port in China between January 2001 and December 2014 were investigated and statistical analysis software R was used to conduct time series analysis on the data.A reasonable model was put forward to describe the change of container throughput data，which was tested and optimized.The container throughput data after ten months was forecasted by using the model.Results showed that the prediction model after time series analysis can well describe the change of the port container throughput，therefore can provide reference for the optimal measures in different periods.

container throughput；time series analysis；forecast；model

2016-03-31

国家留学回国人员科技活动资助项目(人社厅函[2012]258号)

孔琳琳，硕士研究生。研究方向：森林工程。

吴金卓，博士，副教授。研究方向：森林工程，物流工程。E-mail：wujinzhuo1980@163.com

孔琳琳，刘澜，许文秀，等.基于时间序列分析的港口集装箱吞吐量预测分析[J].森林工程，2016，32(5)：106-110.

F 552

A

1001-005X(2016)05-0106-05