关于幂零矩阵的Kronecker积的探讨

武惠俊

（长治学院数学系，山西长治046011）



关于幂零矩阵的Kronecker积的探讨

武惠俊

（长治学院数学系，山西长治046011）

幂零矩阵是一类特殊的矩阵，具有良好的性质.文章主要利用矩阵的特征值，给出了矩阵的Kronecker积仍是幂零矩阵的一个充分必要条件，并且得到了关于幂零矩阵的Kronecker积的幂零指数的两个结论。

幂零矩阵；Kronecker积；特征值

1　引言

幂零矩阵是一类特殊的矩阵,具有很多优良的性质。考虑两个幂零矩阵的Kronecker积何时仍是幂零矩阵是一个重要而有趣的问题。文章主要利用矩阵的特征值概念,给出了矩阵的Kronecker积是幂零矩阵的一个充分必要条件,并且讨论了关于幂零矩阵的Kronecker积的幂零指数。

为了方便，文章在一个固定的数域P中讨论，记Pn×n为数域P上的全体n阶矩阵组成的集合。

2　预备知识

定义1[1]设A∈Pn×n，且A≠0,如果存在正整数k，使得Ak=0，则称A为一个幂零矩阵，使得Ak=0成立的最小的正整数k称为A的幂零指数。

定义2设A=（aij）m×n是m×n矩阵，B=（bij）p×q是p×q矩阵，则称mp×nq矩阵。

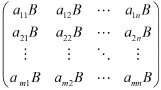
为矩阵A和B的克罗内克（Kronecker）积，记为AUB。

引理1[2]矩阵的Kronecker积有下列运算性质：

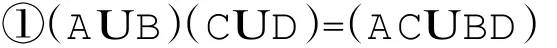
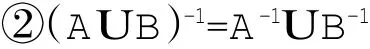
由定义,不难得出：

引理2设A=（aij）m×n是m×n矩阵，B=（bij）p×q是 p×q矩阵,则或B=0。

证明：充分性：显然。

必要性：反证法。若A≠0且B≠0,则A与B中至少都有一个元素不为零,于是AUB≠0，矛盾。

3　主要定理

定理1[3]设A，B分别为m阶和n阶矩阵，它们分别具有特征值λ1，…，λm和μ1，…，μn,则Kronecker积AUB的特征值是λiμj（i=1，…m；j=1，…n）。

证明：由矩阵性质可知，对任意矩阵A，B，都存在可逆矩阵P及Q，使得

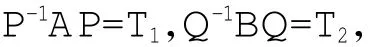
其中T1，T2都是上三角矩阵，其主对角线上的元素分别为矩阵A和B的特征值λ1，…，λm和μ1，…，μn。

由定义可知，上三角矩阵的Kronecker积还是上三角矩阵，即T1UT2为上三角矩阵，并且T1UT2的主对角线上的元素恰为λiμj（i=1，…m；j=1，…n）。由引理1可知，PUQ可逆，且（PUQ）-1=P-1UQ-1于是（PUQ）-1（AUB）（PUQ）=（P-1UQ-1）（AUB）（PUQ）= （P-1APUQ-1BQ）=T1UT2，

故AUB与T1UT2相似，从而有相同的特征值，而T1UT2的特征值就是主对角线上的元素，所以AUB的全部特征值为λiμj（i=1，…m；j=1，…n）。

定理2设A∈Pn×n,则A是幂零矩阵的充要条件是A的特征值皆为0。

证明：先证必要性。设Am=0，由Schur定理,存在可逆矩阵P，使得

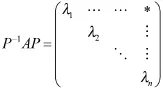
其中λ1，λ2…λn为A的特征值。于是

再证充分性。设A的特征值皆为0，则A的Jordan标准形J的Jordan块只能为

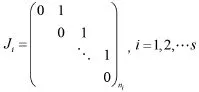
定理3设A，B∈Pn×n,则AUB是幂零矩阵的充要条件是A，B中至少有一个是幂零矩阵。

证明：设A，B的特征值分别为λ1，…，λn和μ1，…μn。

先证条件的充分性。设A，B中至少有一个是幂零矩阵，不妨设A是幂零矩阵，则由定理1，A的特征值λ1，…，λn皆为0。再由定理2，AUB的特征值也全为零，所以AUB是幂零矩阵。

再证条件的必要性。反证法，若A，B都不是幂零矩阵，则A至少有一个特征值不为零，设为λs，1≤s≤n，B至少有一个特征值不为零，设为μt，1≤t≤n，于是AUB至少有一个特征值λsμt不为零，从而AUB不是幂零矩阵，与AUB是幂零矩阵矛盾。

由此定理可得，两个幂零矩阵的Kronecker积仍是幂零矩阵。

推论1有限多个矩阵A1，A2…As的Kronecker积是幂零矩阵的充要条件是A1，A2…As中至少有一个是幂零矩阵。

推论2设A是n阶幂零矩阵,幂零指数为m, B是m阶方阵，且B≠0。则AUB也是幂零矩阵,且幂零指数不超过m。

证明：由引理1，（AUB）m=AmUBm=0UBm=0，于是结论成立。

推论3设A1，A2…As为幂零指数分别为n1，n2…ns的幂零矩阵，则A1UA2U…UAs的幂零指数为n1，n2…ns中的最小者。

证明：令nk=min{n1，n2…ns}，则

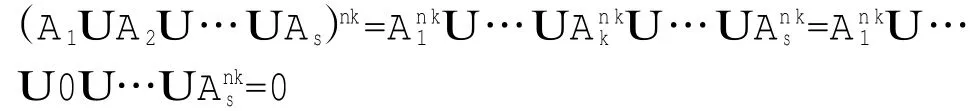
由引理2，nk为使得上式成立的最小的正整数,于是结论成立。

［1］邱森，朱林生.高等代数探究性课题精编［M］.武汉:武汉大学出版社，出版年：2012，172-173.

［2］北京大学数学系前代数小组.高等代数［M］.北京:高等教育出版社，出版年：2013.

［3］晏林.矩阵的kronecker乘积的几个性质[J].云南师范大学学报.2000，（6）：34-35.

（责任编辑赵巨涛）

Wu Hui-jun
（Department of Mathematics Changzhi University,changzhi Shanxi 046011）

O152

A

1673-2014（2016）02-0078-02

2015—11—06

武惠俊（1981—）,女，山西祁县人，讲师，硕士，主要从事有限群表示研究。