饱和分散性土变形特性试验研究

史　祥，樊恒辉，刘　刚，李　普

(1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌　712100；2.中冶南方工程技术有限公司，武汉　430223)



饱和分散性土变形特性试验研究

史祥1,2，樊恒辉1，刘刚1，李普1

(1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌712100；2.中冶南方工程技术有限公司，武汉430223)

目前，人们对于分散性土的研究主要集中在分散性土的鉴定、抗渗和改性等方面，而对其变形特性方面的研究很少。针对此现状，采用单向压缩试验研究了不同压实度下饱和分散性土的变形特性。试验结果表明：饱和分散性土的变形既与应力有关，也与时间有关，且具有明显的非线性特征；压实度对饱和分散性土的变形有显著的影响。试验数据的统计分析表明，饱和分散性土的应力-应变、应变-时间关系均可用幂函数的形式来表述；据此，建立了饱和分散性土的加荷本构模型和蠕变本构模型。通过对模型预测值与实测值的对比分析，发现该模型能够较合理地预测饱和分散性土的变形特性。

饱和分散性土；变形特性；单向压缩试验；幂函数；本构模型

1　研究背景

从渗透稳定和抗水冲蚀破坏的角度，可将黏性土分为分散性土和非分散性土。分散性土是一种在低含盐量水中由于土颗粒间的排斥力大于吸引力而导致土颗粒分散成原级颗粒的土，其工程特性是抗冲蚀性低、抗渗性能差，容易造成堤坝管涌、路堤失稳等工程事故。尽管如此，工程实践证明，只要采取科学合理的措施，就能有效防止分散性土的破坏[1-2]。国内外均有采用分散性土修筑水利工程成功的经验，如：美国墨西哥州LosEsteros大坝、新疆北部额尔齐斯河水利枢纽工程、青岛官路水库、海南岭落水库及宁夏马家树水库等。坝体在运行过程中，其浸润线以下土体常处于饱和状态，而土体的变形特征与其经历的有效应力的变化方式密切相关，当土体处于饱和状态时，其变形特性与非饱和状态时差别较大。因此，研究分散性土在饱和条件下的变形特性具有重要的工程实践价值。

目前，国内外很多学者对饱和土的变形特性进行了研究，并且取得了较多成果。王盛源[3]从理论上分析了饱和黏性土的主固结和次固结变形，并以工程实例验证了饱和软黏土的排水固结沉降。张云等[4-5]用单向固结仪研究了饱和黏性土和饱和砂性土的蠕变特性及蠕变规律，在分析蠕变试验结果的基础上建立了蠕变模型。白冰[6]基于饱和土体的非线性固结变形方程，建立了描述饱和土体非线性固结变形特征的实用理论模型，并通过定义固定参量来描述不同厚度土层固结形态的差异性。秦鹏飞等[7]通过模拟施工过程中扰动土体不同位置的变形和应力状态，探讨了饱和粉土在不同应力路径下的变形特性。蔡袁强等[8]、黄茂松等[9]、王军等[10]、刘添俊等[11]先后从不同角度研究了饱和软黏土在循环荷载作用下的变形特性，并分别探讨了饱和软黏土的变形机理。

对分散性土的研究尚处于探索阶段，因为分散性土在颗粒组成、黏粒含量、孔隙水运移规律等方面均有别于普通黏性土，其固结与变形特性非常复杂，与应力、时间及压实度等密切相关。采用室内单向压缩试验可以对不同压实度的饱和分散性土在自重应力作用下产生的变形沉降量进行预测，而且更接近于工程实际。本文以宁木特水利枢纽工程黏土心墙的分散性土为研究对象，研究饱和分散性土的变形特性及其影响因素，构造侧限条件下垂直压应力与垂直压应变的关系，并将试验结果用于饱和分散性土的变形预测，为实际工程提供一定的理论参考。

2　试验概况

2.1土样性质

试验所用土样取自宁木特水利枢纽工程大坝坝料场地。试验前，采用针孔试验、碎块试验、双比重计试验、孔隙水可溶性阳离子试验以及交换性钠离子百分比试验5种方法综合判定试验土样的分散性。试验表明，该土样具有分散性土的典型特征，属于分散性土。土样的基本物理化学性质指标见表1。试验仪器采用的YS系列高压固结仪见图1，该仪器为单杠杆式加荷系统，加载方式为砝码加载，测量精度为0.001mm。仪器所配备的砝码及百分表均经过国家计量认证。

图1　YS-I型高压固结仪Fig.1　YS-I high-pressure consolidation apparatus

2.2试验方案

试验在室内常温条件下进行，土样面积为50cm2，高度为20mm。所有土样均采用重塑土，取土深度为2.00～4.00m。试验前，对试样进行真空抽气饱和。本次试验按压实度分别为K=90%，92%，94%，96%和98%制样，研究不同压实度条件下饱和分散性土的压缩变形量与变形特性。所有试样采用逐级加载的方式，加载等级分别为50，100，200，400，800kPa，共5级。每级荷载下读数时间为：加载开始起24h内，按照土工试验规程[12]常规固结试验读数频率进行，后期每隔24h观测一次。加载下级荷载是以本级荷载的竖向变形速率在连续24h内的累积压缩变形量小于0.005mm为标准。

3　 试验结果与分析

3.1压缩曲线分析

图2为不同压实度下饱和分散性土的压缩曲线。分析图2(a)可知，轴向应力相同时，孔隙比随压实度的增加而减小，且e-p曲线切线的斜率也随压实度的增大而减小，说明土的压实度越高，压缩系数越小；从图2(b)可以看出，e-lgp曲线切线斜率随轴向应力的增加而增大，随压实度的增加而减小，说明压实度越高，土体的压缩指数越小。

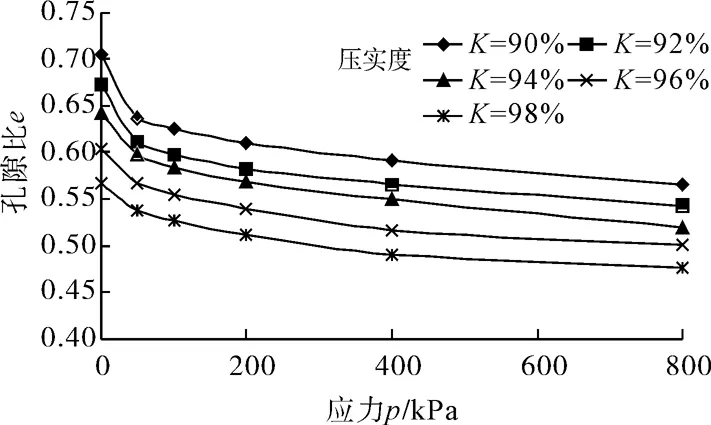
(a)e-p曲线

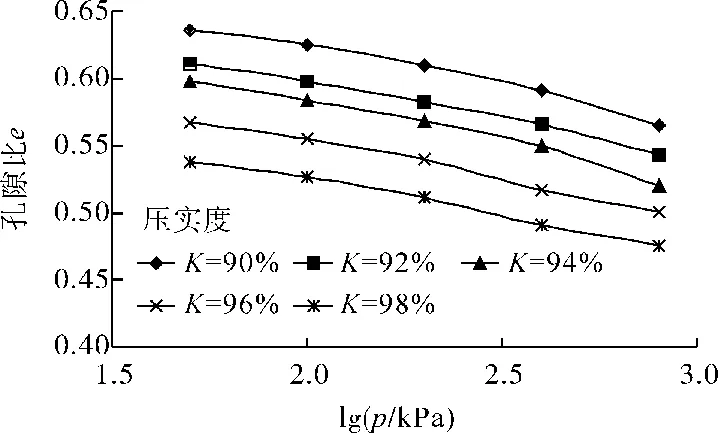
(b)e-lgp曲线图2　不同压实度下e-p曲线与e-lgp曲线Fig.2　Relationships between void ratio and verticalpressure under different degrees of compaction

3.2压缩模量分析

图3为压缩模量随法向应力的变化规律曲线。由图3可以看出，压实度相同时，压缩模量随法向应力的增加而增大；压实度不同时，压实度愈大，压缩模量越大，尤其是在压实度较大，法向应力较大的情况下，压缩模量显著增大。因此，为了减小饱和分散性土体的工后沉降，提高压实度是一种比较有效的方法。

表1　土样的物理化学性质指标Table 1　Physical and chemical indexes of soil samples

注：砂粒粒径为(0.075，2]mm;粉粒粒径为(0.005，0.075]mm;黏粒粒径为<0.005mm。

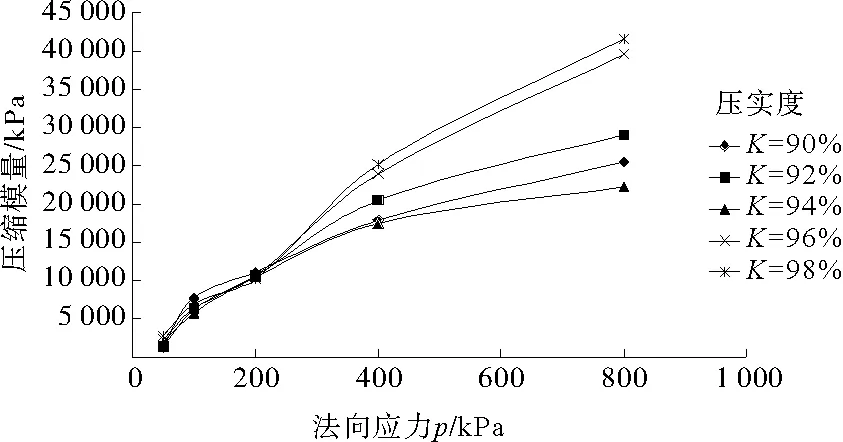
图3　压缩模量与法向应力关系曲线Fig.3　Curves of compression modulus vs.normal stress

3.3蠕变曲线分析

图4是不同压实度试样初次加载时不同荷载作用下变形随时间的变化曲线。由图4可知，在各级荷载作用下，土体的蠕变曲线非常相似，且具有明显的阶段性，主要分为瞬时弹塑性变形、衰减蠕变变形和稳定蠕变变形3个阶段。荷载较小时，土体变形量小且在较短时间内蠕变达到稳定；荷载较大时，土体变形速率增大，蠕变现象较为明显且试样达到变形稳定的时间增长；荷载越大，土体达到变形稳定的时间越长。压实度对饱和分散性土变形影响较为显著，随压实度增加，土体的变形逐渐减小，如压实度为90%时，轴向应力800kPa下的应变为5.02%；压实度为98%时，轴向应力800kPa下的应变为3.695%，应变减小了26%。说明在工程中应尽可能增加土体的压实度，以减弱蠕变带来的危害，提高结构物或构筑物的稳定性。

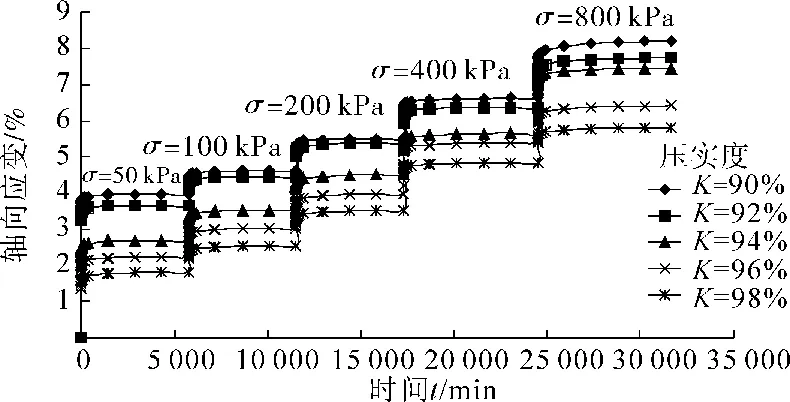
图4　不同压实度蠕变试验曲线Fig.4　Creep curves under different degrees of compaction

3.4等时曲线分析

以90%的压实度为例，土样的应力-应变等时曲线如图5所示。由图5可知，在不同的时刻，其应力-应变曲线都呈现显著的非线性特征，且随应力增大，等时曲线的非线性程度增大，说明非线性程度随应力的增加而增大。

以上的试验结果表明，分散性土的应力-应变、应变-时间关系是非线性的。

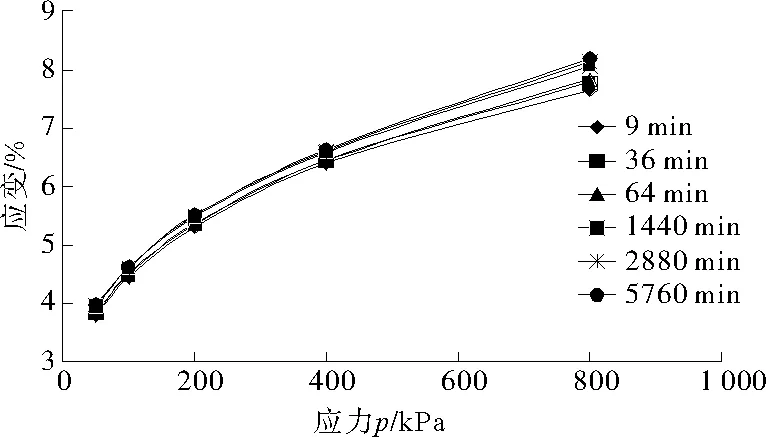
图5　蠕变等时曲线(压实度90%)Fig.5　Isochronous curves of creep(compactiondegree K=90%)

4　饱和分散性土本构模型

4.1应力-应变本构模型

本文在大量室内试验的基础上，分别采用双曲函数和幂函数拟合饱和分散性土的应力-应变关系，试验数据和拟合曲线如图6、表2所示。

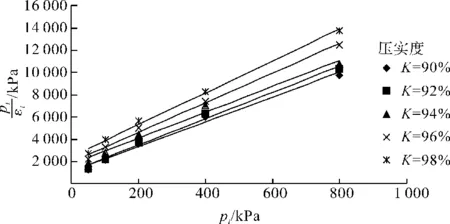
(a)pi/εi-pi关系曲线

(b)ln(pi/εi)-lnpi双对数关系曲线图6　饱和分散性土应力-应变关系Fig.6　Stress-strain curves of saturated dispersive clay表2　饱和分散性土应力-应变关系拟合曲线Table 2　Stress-strain fitting curves of saturated dispersive clay

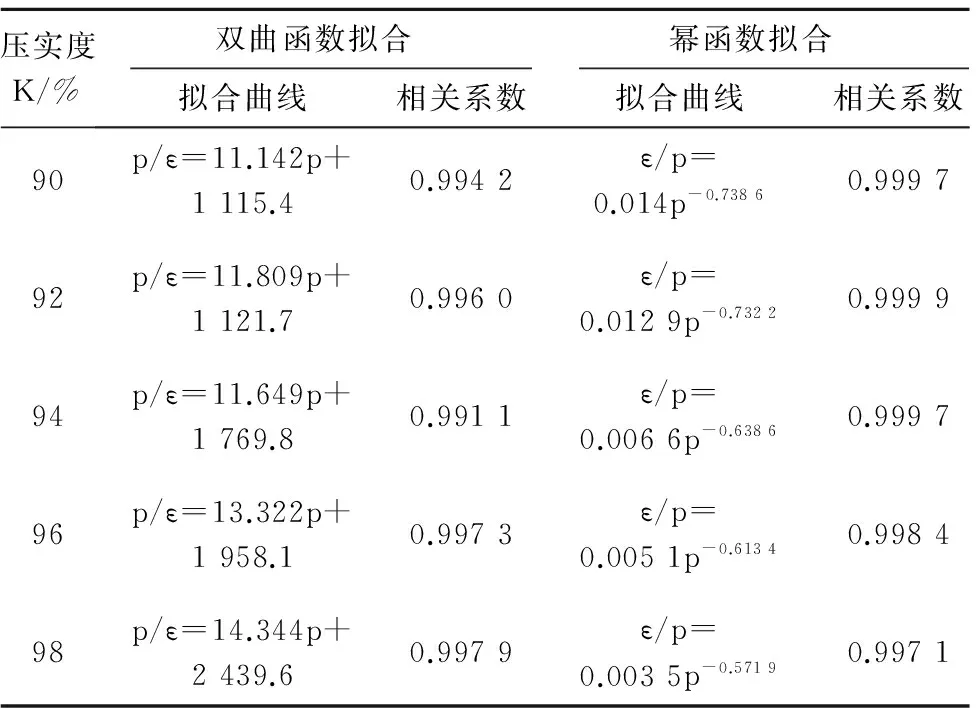
压实度K/%双曲函数拟合幂函数拟合拟合曲线相关系数拟合曲线相关系数90p/ε=11.142p+1115.40.9942ε/p=0.014p-0.73860.999792p/ε=11.809p+1121.70.9960ε/p=0.0129p-0.73220.999994p/ε=11.649p+1769.80.9911ε/p=0.0066p-0.63860.999796p/ε=13.322p+1958.10.9973ε/p=0.0051p-0.61340.998498p/ε=14.344p+2439.60.9979ε/p=0.0035p-0.57190.9971

由表2可知，采用幂函数拟合饱和分散性土的应力-应变关系，其相关系数更接近于1，说明幂函数在一定程度上更能反映饱和分散性土的应力-应变特性。

4.2蠕变本构模型

张云等[4-5]在对饱和黏性土、饱和砂性土的蠕变研究中拟合了应变与应力、时间的关系式，本文以类似的方法着重拟合饱和分散性土应变随应力及时间的变化关系。图7为应变-时间双对数关系曲线。

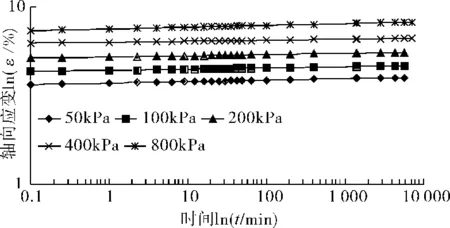
图7　双对数坐标中的蠕变曲线(压实度90%)Fig.7　Creep curves in log-log coordinates(K=90%)

以90%的压实度为例，由图7可知，在相同压实度、不同荷载作用下的试验曲线近似为直线，且直线斜率的绝对值近似相等。因此，在某一时刻、不同应力作用下，应变-时间的关系曲线可以表示为

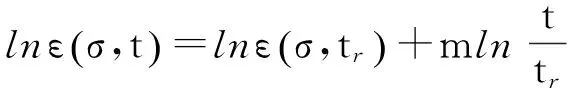
(1)

由式(1)可得

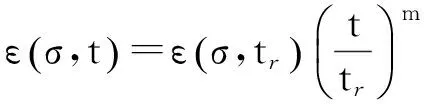
(2)

图8为应力-应变双对数关系曲线，即将等时曲线分别表示在双对数坐标系中。

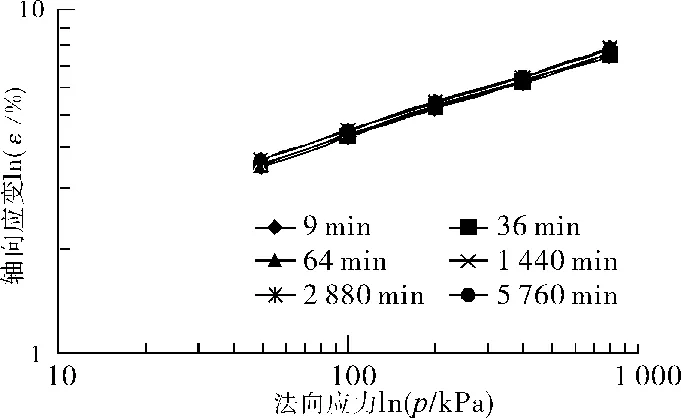
图8　双对数坐标中的等时曲线(压实度92%)Fig.8　Isochronous curves in log-log coordinates(K=92%)

以92%的压实度为例，由图8可知，在相同压实度、不同时刻的应力-应变等时曲线近似为直线。因此，在不同时刻、某一应力作用下，应力-应变的关系曲线可以表示为

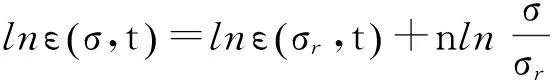
我姨妈和同学们扮成染了传染病的男孩，在金陵医学院的病号房藏了两天，又被偷偷地送到南京附近的乡下，再从那里乘船到芜湖，而后转船去了汉口。法比·阿多那多一路护送，身份从神甫变成了监护“医生”。谁也没想到，那次临时的职业伪装永久地改变了法比的身份。半年后他回到南京，辞去了教堂的职务，在威尔逊教会学校教世界历史和宗教史，在其他大学零散兼课，那十三个被秦淮河女人顶替下来的女孩中，唯有我姨妈孟书娟一直和他通信，因为她和他都存在一份侥幸，万一能找到十三个女人中的某一个，或两个，即便都找不到，得到个下落也好，别让他们的牵记成为永远的悬疑。

(3)

由式(3)可得

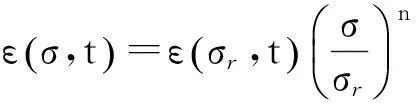
(4)

由式(4)可得

(5)

将式(5)代入式(2)，可得

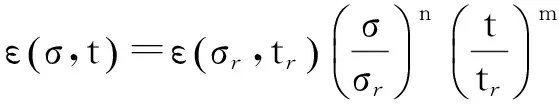
(6)

当t=0时，式(6)为

(7)

由以上可知，饱和分散性土蠕变方程可表示为

(8)

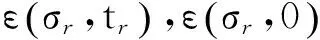
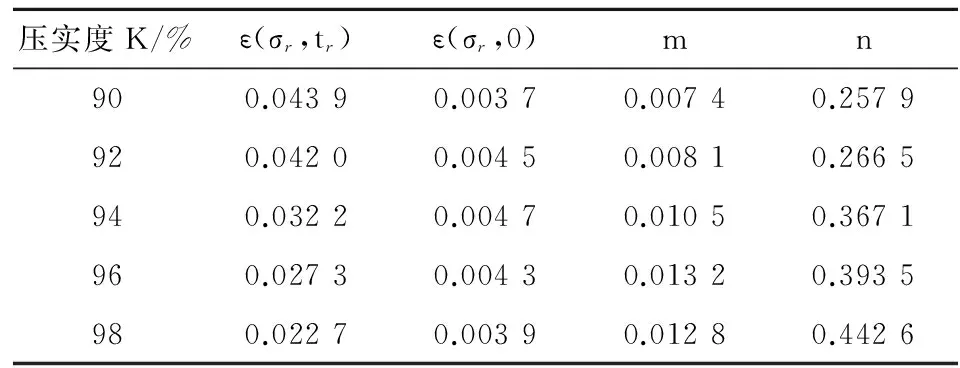
表3　饱和分散性土蠕变参数Table 3　Creep parameters of saturated dispersive clay

将表3蠕变参数代入蠕变方程并与试验结果进行拟合，以92%和94%的压实度为例，结果如图9所示。

(a)压实度92%

(b)压实度94%图9　饱和分散性土蠕变模型计算结果与试验数据对比Fig.9　Comparison between calculated values from creepmodel and testing data of saturated dispersive clay

分析图9可知，轴向应力较小时，模型预测值与实测值基本一致；轴向应力较大时，随蠕变时间的延长，预测值比实测值有所升高，但升高的幅度不大，从工程角度讲是偏于安全的。总体来说，模型的预测值与实测值吻合较好，该模型可以准确地描述饱和分散性土的蠕变特性。

5　结　论

通过对宁木特水利枢纽工程黏土心墙的分散性土在饱和条件下的变形特性分析，得到以下结论：

(1)饱和分散性土的蠕变具有明显的阶段性，其变形分为瞬时弹塑性变形、衰减蠕变变形和稳定蠕变变性3个阶段；应力-应变等时曲线表明，饱和分散性土的应力-应变关系具有明显的非线性特征。

(2)单向压缩试验表明，侧限条件下的应力-应变关系可以用幂函数进行拟合，其相关系数更接近于1且稳定性较好，可以用来描述饱和分散性土的应力应变特性。

(3)饱和分散性土的应变与时间、应力与应变关系均可以用幂函数描述，且建立的蠕变本构模型用于预测土体后期的变形是偏于安全的，可以作为饱和分散性土的蠕变预测模型。

研究成果可供分散性土防渗心墙及防渗渠土体的工后变形预测、安全性评价和参考，具有一定的实际应用价值。

[1]钱家欢.分散性土作为坝料的一些问题[J].岩土工程学报,1981,3(1):94-100.

[2]陈劲松,顾缬琴,盛小涛,等.大坝心墙料分散性及处理措施试验研究[J].长江科学院院报,2016,33(4):144-150.

[3]王盛源.饱和粘性土主固结与次固结变形分析[J].岩土工程学报,1992,14(5):70-75.

[4]张云,薛禹群,吴吉春,等.饱和黏性土蠕变变形试验研究[J].岩土力学,2011,32(3):672-683.

[5]张云,薛禹群,施小清,等.饱和砂性土非线性蠕变模型试验研究[J].岩土力学,2005,26(12):1869-1873.

[6]白冰.饱和土体固结变形特征的一种非线性描述[J].岩石力学与工程学报,2005,24(11):1966-1971.

[7]秦鹏飞,谢晓杰,马玉林.不同应力路径下饱和粉土强度与变形特性试验研究[J].长江科学院院报,2016,33(4):78-80.

[8]蔡袁强,王军,海钧.双向激振循环荷载作用下饱和软黏土强度和变形特性研究[J].岩石力学与工程学报,2008,27(3):495-504.

[9]黄茂松,李进军,李兴照.饱和软粘土的不排水循环累积变形特性[J].岩土工程学报,2006,28(7):891-895.

[10]王军,蔡袁强.循环荷载作用下饱和软黏土应变累积模型研究[J].岩石力学与工程学报,2008,27(2):331-338.

[11]刘添俊,葛修润,安关峰.单向循环荷载作用下饱和软黏土的性状研究[J].岩石力学与工程学报,2012,31(增1):3345-3351.

[12]GB/T50123—1999,土工试验方法标准[S].北京:中国计划出版社,1999.

[13]魏汝龙.直剪固快试验结果的整理和分析[J].地基处理,1999,10(4):15-18.

[14]黄雪峰,孔洋,李旭东,等.压实黄土变形特性研究与应用[J].岩土力学,2014,35(增2):37-44.

[15]陈开圣,沙爱民.压实黄土变形特性[J].岩土力学,2010,31(4):1023-1029.

[16]刘保健,谢定义,郭增玉.黄土地基增湿变形的实用算法[J].岩土力学,2004,25(2):270-274.

[17]刘保健,张军丽.土工压缩试验成果分析方法与应用[J].

中国公路学报,1999,12(1):37-41.

(编辑：刘运飞)

Deformation Properties of Saturated Dispersive Clay

SHI Xiang1,2,FAN Heng-hui1,LIU Gang1,LI Pu1

(1.CollegeofWaterResourcesandArchitecturalEngineering，NorthwestA&FUniversity，Yangling712100，China； 2.WISDRIEngineering&ResearchIncorporationLimited，Wuhan430223，China)

Dispersiveclayisoflowerosionresistanceandimpermeability,andseverelyendangersthesafetyofwaterconservancyconstructionasithashighdispersioninlowsalinitywater.Atpresent,researchofdispersiveclaymainlyfocusesontheidentification,impermeabilityandmodification;however,studiesonthedeformationpropertiesarerare.Inthispaper,thedeformationbehaviorofsaturateddispersiveclayunderdifferentdegreesofcompactionwasstudiedthroughuniaxialcompressiontests.Thetestresultsshowthatthedeformationofdispersiveclaydependsnotonlyonthestressesexertedonthembutalsothetimeelapsed,andhasobviousnonlinearcharacteristics.Theresultsalsoindicatethatthedegreeofcompactionhassignificanteffectonthedeformationofsaturateddispersiveclay.Accordingtothetestresults,thestress-strainandstrain-timecurvesofsaturateddispersiveclaycanbeexpressedwiththepowerfunction.Theloadingconstitutivemodelandcreepconstitutivemodelwereestablished,andthecomparisonbetweenmodelpredictedresultandmeasuredresultindicatesthatthepredictedresultusingthemodelareinreasonableagreementwiththetestdata.

saturateddispersiveclay;deformationproperties;uniaxialcompressiontests；powerfunction;constitutivemodel

2015-08-05;

2015-10-06

国家自然科学基金项目(51379177，51579215);中央高校基本科研业务费专项资金项目(ZD2013013)

史祥(1988-)，男，湖北襄阳人，硕士研究生，主要从事特殊土的工程性质等方面的研究，(电话)13689244595(电子信箱)shixiang0618@163.com。

樊恒辉(1973-)，男，山西夏县人，研究员，博士，博士生导师，主要从事特殊土的工程性质、土质化学加固原理与技术、环境岩土工程等方面的研究，(电话)029-87082884(电子信箱)yt07@nwsuaf.edu.cn。

10.11988/ckyyb.20150630

2016,33(09):87-92

TU411

A

1001-5485(2016)09-0087-06