基于IDDQ测试的VLSI门内电阻式桥接故障仿真

许爱强，唐小峰，2，牛双诚，杨智勇，3

（1.海军航空工程学院科研部，烟台 264001；2.中国人民解放军92514部队，烟台 264007；3.中国人民解放军91370部队，福州 350015）

基于IDDQ测试的VLSI门内电阻式桥接故障仿真

许爱强1，唐小峰1，2，牛双诚1，杨智勇1，3

（1.海军航空工程学院科研部，烟台 264001；2.中国人民解放军92514部队，烟台 264007；3.中国人民解放军91370部队，福州 350015）

为真实模拟集成电路中的桥接故障并评价测试集质量，提出一种基于静态电源电流（IDDQ）测试的逻辑电路门内电阻式桥接故障仿真算法.首先，针对该故障类型，提出一种覆盖率评价标准；其次，利用电路级故障注入与仿真方法构造基本逻辑门单元的故障字典；最后，通过在逻辑电路功能仿真中查询故障信息实现门级的故障仿真.仿真实验表明：相比于传统方法，所提方法能更好地反映测试集对真实桥接故障的覆盖效果，并具备良好的仿真效能.

超大规模集成电路（VLSI）测试；电阻式桥接故障；静态电源电流（IDDQ）测试；故障仿真；故障覆盖率

应用真实的故障模型来评价超大规模集成电路（very large scale integration，VLSI）测试集质量一直以来都是VLSI测试领域的重要研究目标.桥接故障（bridging fault，BF）是VLSI中最常见的故障之一，尤其是随着电路集成密度的不断增加，其重要性越发凸显.许多相关研究假定桥接阻值为0 Ω［1］或者为某一固定值［2］.然而，理论上实际桥接阻值可能分布于0到无穷大的动态区间上，是一个随机变量.这给VLSI的测试带来了新的挑战.针对这一问题，电阻式桥接故障（resistive bridging fault，RBF）在近年来得到广泛研究［3-5］.按RBF发生位置的不同，可以将其分为门间（inter-gate）RBF和门内（intra-gate）RBF两类.许多研究关注门间RBF，鲜有对门内RBF的研究报道.然而，考虑到：1）门内RBF是一种局部故障模型，桥接故障点之间距离相近，在实际电路中发生的可能性较高；2）由于被测电路（circuit under test，CUT）的最终布局实现往往难以获得，门间RBF通常需要考虑所有的连线组合，其计算复杂度为O（m2），其中m为CUT中连线的数量［6］，而门内RBF的计算复杂度要小得多，为O（n），其中n为CUT中逻辑门的数量；3）门内RBF可达逻辑门电路中的内部节点（internal nodes）［6］，而门间RBF则不能.因此，研究VLSI的门内RBF具有现实意义.目前，研究VLSI桥接故障的方法主要有电压测试法（逻辑测试）和供电电流测试法2 类.前者需将故障的影响传播到CUT的原始输出端；而后者需在CUT中设置额外的电流监控器.有研究表明，静态电源电流（IDDQ）测试对桥接故障的覆盖效果通常要好于逻辑测试［7］.因此，本文基于IDDQ测试研究VLSI中的门内RBF仿真问题.

1　门内RBF及其覆盖率模型

这里研究门内RBF（以下简称RBF）的目的是考察这类故障如何在单个逻辑门的局部范围内对整个被测电路（circuit under test，CUT）的IDDQ特征产生影响.在两点间桥接假设下，一个RBF可被定义为f=〈n1，n2，R〉，其中n1和n2是被短接的电路节点，它们既可以是外部连线也可以是内部节点；R为桥接阻值随机变量.特别地，当R=0时，即为理想桥接故障；当R=C（C为固定常数）时，则为固定阻值桥接故障.

以图1（a）所示的两输入CMOS与非门为例，一个RBF：f=〈LA，LC，RB〉发生在连线LA和内部节点NC之间，桥接阻值R=RB.假设给定测试激励t= “11”（LA=‘1'，LB=‘1'），正常状态下PMOS管M1和M2截止，NMOS管M3和M4导通.由于晶体管截止电阻通常很大，以至于IDDQ值非常小（≤nA数量级）.然而，由于桥接故障f的影响，输入线LA上的电平被拉低，这可能致使以其作为输入控制端的晶体管M2和M3工作于非稳定的可变电阻区.图1（b）显示了该与非门电路在f存在时的一个等效电路，其中RUP是前级驱动门的上拉网络等效电阻；RON是晶体管的导通电阻；而晶体管的截止电阻则被忽略.这样，电路中就形成了导通VDD和地的通路，使得IDDQ急剧增大，以至达到可检测的水平.根据电路方程不难得到

图2中所示为对该与非门电路的桥接阻值执行参数扫描分析得到的关系曲线IDDQ（r）.可见，IDDQ与桥接阻值r成反比关系.值得注意的是，对不同的RBF，上述IDDQ的表达式也不相同，并由于晶体管的阻值非线性且与桥接阻值耦合，难以用解析的方法求解RBF存在时的IDDQ.因此，本文采用电路仿真的方案解决该问题.

假设IDDQ监控器的检测门限为ITH，其对应的临界桥接阻值为RTH，如图2所示，则当≥ITH时，监控器将产生告警，表明故障被检测到.因此，对任意一个电阻式桥接故障f，忽略系统噪声和测量误差的影响，它被检测到的概率为

式中η（r）为桥接阻值分布的概率密度函数.覆盖率FCf，t表示在当前测试激励t下，以ITH为门限，通过测量IDDQ覆盖f全部阻值区间的概率.进一步，对于测试集T=｛t1，t2，…，tn｝，其对故障f的覆盖率定义为

式（4）表示如果测试集中有多个测试覆盖f，则选取覆盖率最大的一个代表整体的故障检测能力.

最后，定义测试集 T对 RBF故障集 F=｛f1，f2，…，fm｝的覆盖率为

式中m为CUT中RBF的数量.

2　RBF仿真算法

RBF仿真算法包括2个阶段：电路级仿真和门级仿真.电路级仿真的任务是基于RBF模型为基本逻辑门生成故障字典；门级仿真则是通过在功能仿真过程中引入字典中记录的故障信息实现对测试集故障覆盖率的评估.

2.1电路级仿真

电路级仿真的自动实现流程如图3所示.给定目标门电路的描述，首先将其解析为一种易于实现RBF注入的内部模型［8］，随后故障注入模块根据给定的桥接节点和阻值生成原电路的故障版本.仿真器调用PSpice仿真程序将故障电路置于不同的测试输入组合下进行仿真，得到电路的IDDQ测量值.分析器将 IDDQ与 ITH进行比较，若刚好满足 IDDQ= ITH，则令RTH=R，否则调整R的值并继续搜索RTH.最后，将得到的RTH保存在故障字典中.

后来真相大白，镯子是被怡红院的坠儿偷了去。但那句“本来又穷”已经把人赤裸裸地定在了道德的耻辱柱上，动弹不得、翻身不得。

电路级仿真的关键步骤是搜索RTH，考虑到阻值搜索空间无上界（下界为0），这里采用动态边界折半搜索算法查找临界阻值RTH，算法流程如下.

算法1 动态边界折半搜索算法

2）令R=RINI（初始值RINI＞0），RL=RH=0，执行一次RBF仿真.若|-ITH|≤ε，0＜ε≪1，终止算法并返回RTH=R，否则继续.

值得注意的是，在构建故障字典时，应首先仿真一次无故障电路，获取当前桥接节点n1和n2上的电压值，只有当两节点电压值不等时才有必要启动故障仿真.

2.2门级仿真

门级RBF仿真的实现过程如图4所示，其输入为CUT的门级网表描述，经过解析后转换为一种内部表示（包含构成CUT的逻辑门列表及其连接关系等信息）.仿真器利用测试生成器输出随机测试序列，同时结合故障字典中记录的故障信息，执行CUT的功能仿真和故障仿真.最后按式（5）计算测试集T对RBF故障集F的覆盖率.

门级的故障仿真以正常的逻辑电路功能仿真为基础.为此，首先实现了一种事件驱动的组合逻辑电路功能仿真算法.其主要思想是以CUT中信号值的变化为事件，当一个门的输入信号上有事件发生时便调度这个门，并利用其输出信号的变化产生新的事件，以驱动后续仿真的运行，直到CUT中不再产生新的事件为止.每步仿真时刻被划分为若干无限小的δ-周期，每个δ-周期处理当前的事件并调度相应的门，并为下一个δ-周期产生事件.这样就能有效模拟实际逻辑电路中的器件并发行为［9］.具体实现见算法2.

算法2 逻辑电路功能仿真

1）根据当前CUT原始输入端上的测试序列t，生成初始事件并赋给事件集E.令即将被调度执行的门的集合P=⊘.

2）若E=⊘，则终止当步仿真，否则根据E确定P中的元素.设e∈E，且与e关联的信号为s，则将以s为输入信号的门作为P元素的候选，再从中选择输入级数最小的门添加至P中.连线的输入级数算法参见文献［10］，越靠近原始输入端的连线输入级数越小，而门的输入级数则等于其输出连线的输入级数.

3）令E=⊘，调度执行P中所有的门，并将由于其输出信号改变而产生的新事件添加至事件集E，转到步骤2）.

与基于逻辑测试的故障仿真算法不同，基于IDDQ测试的算法无需向CUT中实际注入逻辑故障，而只需仿真一次无故障情形，然后基于连线上的逻辑值查询故障字典得到RTH，再通过式（3）（4）确定测试集对当前故障的覆盖率.最终的测试集对由所有RBF构成的故障集的覆盖率由式（5）算得.

3　仿真实验及结果分析

首先为若干CMOS基本逻辑门构建了故障字典，包括反相器，缓存器，两输入与门、或门、与非门、或非门和异或门.表1中为给定ITH=100 μA时两输入与非门（如图1（a）所示）的故障字典实例.其中第1列为该门电路中所有可能的14个RBF；第2～5列为某一RBF分别在不同测试下对应的临界阻值RTH.晶体管仿真计算模型来自Cadence公司OrCAD 16.3设计软件中提供的器件模型库，NMOS 和PMOS管分别使用其默认的MBreakN和MBreakP模型.

表1　两输入CMOS与非门的故障字典Table 1 Fault dictionary of CMOS nand-2 gate kΩ

注意到覆盖率与RTH成正比，因此要获得最大的故障覆盖率，测试集应使逻辑门的输入对应故障字典中的最大临界阻值.例如，对于节点对〈LZ，LA〉，测试“00”的覆盖率高于其他测试的覆盖率，因此，应尽量使与非门的输入端出现“00”以使得〈LZ，LA〉上的RBF能够获得最大的覆盖率.然而，若要得到关于表1中所有RBF的最大覆盖率，显然要求测试集能够遍历该与非门的所有输入组合.若测试生成技术难以满足上述要求，则应首先满足平均临界阻值最大的输入测试.如表1中的“01”，其平均覆盖率好于其他测试.

由于实际电路中的桥接阻值R是分布于（0，+∞）上的随机变量，因此，一种比较合理的假设是R服从对数正态分布

式中：σ＞0；μ为实数.在这一假设下式（3）可简化为

实际应用中，应根据历史故障信息或经验对桥接阻值的分布参数进行估计.而作为仿真实验，这里取μ=9，σ=1，由此可得桥接阻值的期望值为exp（μ+σ2/2）=13.36 kΩ.

表2给出了针对ISCAS'85组合逻辑基准电路开展RBF仿真实验的结果.其中，第1列为CUT的名称；第2列为CUT的规模，即包含的基本逻辑门数量；第3列为CUT中所有被仿真RBF的数量；第4列为假定R=0 Ω时，所有可能被IDDQ测试检测到的RBF的数量；第5列为基于传统BF覆盖率计算方法得到的覆盖率［6］，BF-FC的值等于第4列数据与第3列的比；第6列为假设桥接阻值取对数正态分布并根据本文所提方法计算得到的RBF覆盖率.故障仿真实验中，c17的测试集规模为V=32（已穷举其所有输入组合），其余基准电路采用随机生成的测试序列，测试集规模均为V=105（详见表3）.

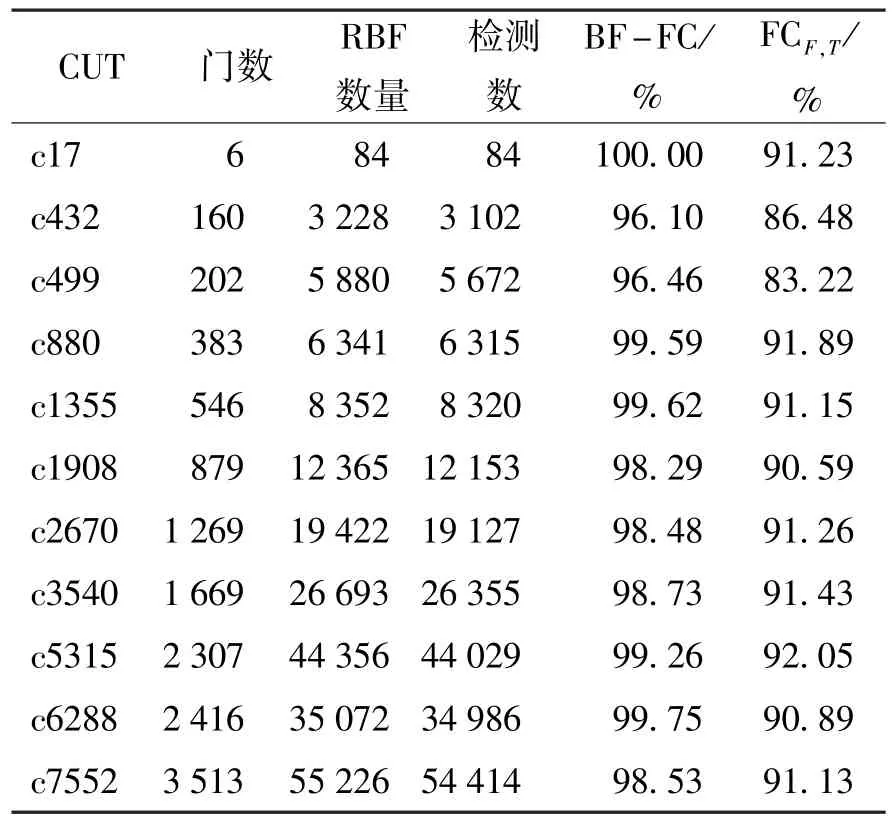
表2　组合基准电路RBF仿真结果（ITH=100 μA）Table 2 RBF simulation results of the benchmarks （ITH=100 μA）

由表2可见，相比于传统的基于IDDQ的理想BF测试，相同测试集对RBF的覆盖率明显偏小.这说明传统方法存在覆盖率虚高的情况，而基于此生成的测试集将难以保证CUT中的真实桥接故障被有效地检测到，继而影响最终产品的可靠性.

表3中所列数据为将本文所提方法的仿真效能与文献［3］相比较所得结果.其中，第1列为CUT名称；第2～5列为文献［3］中的数据；第6～9列为本文所得数据.符号V、B、K分别表示测试用例数量、被仿真的RBF数量和仿真时间消耗.K/（BV）是归一化的仿真效能衡量指标，其值越小效能越高.文献［3］的仿真实验环境为Linux操作系统、2.8 GHz AMD Opteron CPU及16 GB RAM.本文中仿真实验的硬件配置为Windows 7操作系统、3.4 GHz Intel Core CPU和4 GB RAM，算法实现的软件环境为Visual Studio 2010 C#4.0.通过比较可见，本文所提算法效能与文献［3］总体相当，两者效能指标相对起伏的主要原因是目标故障类型不同：文献［3］中主要研究门间RBF，而本文针对门内RBF，因此在故障仿真算法上存在差异.另外值得注意的是，由于门间RBF需考虑全局节点的各种组合，其故障规模成几何级数增长，故对于较复杂电路，文献［3］中将故障数量限定为104（如表3中第3列的3～10行所示），而本文所研究的门内RBF规模与CUT中逻辑门数量成线性递增关系，因此通常情况下能够遍历所有故障.

表3　故障仿真效能比较Table 3 Comparison with previous work

由式（3）可知，影响最终覆盖率指标的因素有2个：桥接阻值分布η（r）和临界阻值RTH.图5所示为满足对数正态分布（μ=9）的桥接阻值在不同的均方差σ下，故障覆盖率的变化情况，其中目标电路为c432基准电路.可见，随着σ的增加覆盖率逐渐降低.这是由于σ越小概率密度曲线收缩得越紧，通过积分求得的FCf，t就越大（假设RTH足够大），最终求得的平均覆盖率也就越高.然而，无论桥接阻值分布如何，RBF覆盖率都不会超过传统的BF.这再次说明，传统方法过于理想化，结果偏乐观.

图6所示为覆盖率在不同的ITH设定下的变化趋势（目标CUT仍为c432）.显然，ITH越小（RTH越大）覆盖率越高.并且基于RBF的覆盖率随着ITH的变小逐渐趋于理想值BF-FC.然而，实际应用中并非ITH越小越好.首先，要综合考虑高精度电流测量的实现难度和成本；其次，电流门限过小将使系统抗噪能力下降，造成虚警率增高，适得其反.本文所提方法为集成电路IDDQ测试方案中ITH的选取提供了参考.就本次仿真实验所采用的CMOS工艺、桥接阻值分布和目标电路c432而言，取ITH=50 μA即可获得较好的故障覆盖效果.

4　结论

1）在面向故障的集成电路测试中测试覆盖率受桥接阻值分布影响明显，传统的方法假设桥接阻值趋于零，得到的结果过于乐观.

2）IDDQ测试中门限电流的设定十分关键，需综合权衡虚警、成本和故障覆盖率等要素，本文所提方法可为解决此问题提供一种参考.

3）采用层次化的电路级和门级2级故障仿真算法，可显著提高仿真效能，增强了处理大规模的故障样本的能力，有助于提升测试集的质量.此外，门级的故障仿真结果又可作为更高电路设计抽象层次（如寄存器传输级等）故障仿真的基础，从而进一步扩展方法的应用前景.

［1］POLIAN I，ENGELKE P，BECKER B.Efficient bridging fault simulation of sequential circuits based on multi-valued logics［C］∥Proceedings of IEEE International Symposium on Multiple-Valued Logic.Boston：IEEE，2002：216-222.

［2］马岚，王厚军.基于输出电压和电源电流协同分析的故障诊断方法［J］.仪器仪表学报，2013，34（8）：1872-1878. MA L，WANG H J.Fault diagnosis method based on output voltage and supply current collaborative analysis ［J］.Chinese Journal of Scientific Instrument，2013，34 （8）：1872-1878.（in Chinese）

［3］ENGELKE P，BECKER B，RENOVELL M，et al. SUPERB：simulator utilizing parallel evaluation of resistive bridges［J］.ACM Transactions on Design Automation of Electronic Systems，2009，14（4）：56.

［4］ZHONG S，KHURSHEED S，AL-HASHIMI B M.A fast and accurate process variation-aware modeling technique for resistive bridge defects［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2011，30（11）：1719-1730.

［5］AZEVEDO J，VIRAZEL A，BOSIO A，et al.Impact of resistive-bridge defects in TAS-MRAM architectures［C］∥Proceedings of IEEE Asian Test Symposium（ATS）. Niigata：IEEE，2012：125-130.

［6］CHAKRAVARTY S，THADIKARAN P J.Simulation and generationofIDDQtestsforbridgingfaultsin combinationalcircuits［J］.IEEETransactionson Computers，1996，45（10）：1131-1140.

［7］RAJSUMAN R.Iddq testing for CMOS VLSI［J］. Proceedings of the IEEE，2000，88（4）：544-568.

［8］XU A Q，TANG X F，YANG Z Y.Mutant generation for analog circuitdesigns［C］∥ ProceedingsofIEEE International ConferenceonSoftwareEngineeringand Service Sciences.Beijing：IEEE，2014：916-920.

［9］李晓维，吕涛，李华伟，等.数字集成电路设计验证——量化评估、激励生成、形式化验证［M］.北京：科学出版社，2010：12-18.

［10］王新安，蒋安平，宋春殚，等.数字系统测试［M］.北京：电子工业出版社，2007：48-49.

（责任编辑 吕小红）

Simulation of Intra-gate Resistive Bridging Faults in VLSI Based on IDDQ Testing

XU Aiqiang1，TANG Xiaofeng1，2，NIU Shuangcheng1，YANG Zhiyong1，3
（1.Department of Scientific Research，Naval Aeronautical and Astronautical University，Yantai 264001，China；2.Unit 92514 of the PLA，Yantai 264007，China；3.Unit 91370 of the PLA，Fuzhou 350015，China）

To realistically simulate the bridging faults in VLSI and to evaluate the quality of the test set，an intra-gate non-zero resistance bridging fault simulation algorithm based on IDDQ testing was proposed. First，a fault coverage criteria was proposed for this type of fault.Second，the fault dictionary for every type of the primitive logic gate cells was constructed by using the circuit-level fault injection and simulation method.Lastly，the gate-level fault simulation was accomplished by querying the fault dictionary when performing the functional simulation of the target logic circuit.Experimental results show that，comparing with the traditional approach，the proposed method in this paper can better reflect the fault covering ability of the test set against the realistic bridging faults and the simulation is efficient.

VLSI testing；resistive bridging fault；IDDQ testing；fault simulation； fault coverage

TP 391

A

0254-0037（2016）01-0128-06

10.11936/bjutxb2015040078

2015-04-25

“泰山学者”建设工程专项经费资助项目；中国博士后科学基金资助项目（2013M542535）

许爱强（1963—），男，教授，主要从事电子信息系统测试与诊断技术方面的研究，E-mail：vivorimage@126.com