某型舰船危险部位结构可靠性分析

黄金娥，刘隆波（海军装备研究院，北京 100073）

某型舰船危险部位结构可靠性分析

黄金娥，刘隆波
（海军装备研究院，北京 100073）

在响应面随机有限元法和结构可靠性理论的基础上，利用有限元软件 Ansys 建立某型舰船开口结构的梁板模型，采用改进的一次二阶矩法与分枝限界法、概率网络评估技术分析了开口结构在组合载荷作用下的可靠性。以结构的最危险点应力为输出变量，通过敏度分析忽略最大应力不敏感的变量拟和响应面方程。利用随机有限元和 CAE 软件结合开展结构系统的可靠性研究，避免了大型结构寻找失效模式的困难，使可靠性分析的效率得到极大提高。

开口结构；随机有限元；响应面；结构可靠性

0　引 言

舰船结构系统日趋复杂，可靠性要求越来越高，对舰船结构进行随机分析并评价其可靠性就显得非常必要。由于舰船结构体系庞大，影响其可靠性的随机变量多，从而使结构失效模式的判别及失效概率的计算效率十分低下，因此系统可靠性分析在船舶结构中非常困难。利用随机有限元方法和现有的大型 CAE 软件结合对结构系统开展可靠性研究可以大幅节省时间和经费，是一种很有应用前景的方法［1］。

本文基于响应面随机有限元法和结构可靠性理论，采用改进的一次二阶矩法与分枝限界法、概率网络评估技术分析某开口结构的可靠性，并利用有限元软件 Ansys 建立了某型舰船开口结构的梁板模型，分析了开口结构在组合载荷作用下的可靠性。

1　开口结构可靠性模型

某舰根据功能需要，在舰尾部位#241 肋位～#220肋位的一甲板、二甲板处开设了一个矩形口。开口周围为了增强结构的整体性增加甲板的厚度、增设了加强梁。舰底部采用部分双层底结构。舰主体采用纵骨架结构，开口处 4个角点有集中载荷，均值为 0.425 × 106 N。

为了验证该型舰的结构可靠性是否满足规定要求，建立#250 肋位～#211 肋位舱段的随机有限元和可靠性分析模型。

舰体局部结构模型，使用 SHELL 63 板壳元和BEAM 188 梁元，将舰体局部结构几何模型划分有限元模型。SHELL 63 单元是具有弯曲刚度的板壳单元，能够较好模拟舱段的各种板壳元件。BEAM 188 单元能定义梁元的截面形状，如工字梁、球扁钢等，所以能够用来模拟舱段中的各种梁元件。BEAM 188 适用于分析细长的梁［2］。

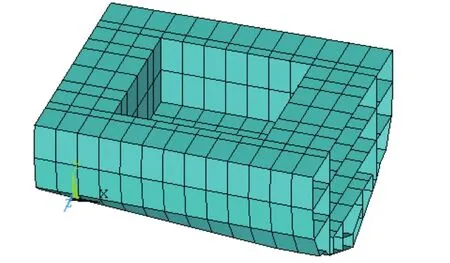
图1　开口部分的计算模型Fig.1　Computing model of opening structure

2　可靠性功能函数

对于该船体局部结构，其功能函数可写成

式中：｛X｝为基本随机变量向量；N为基本随机变量个数。

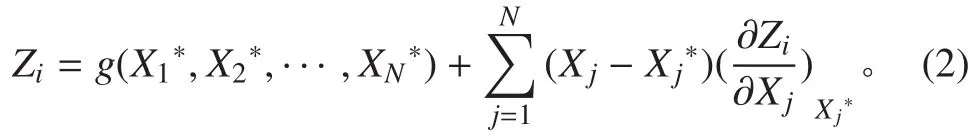
Zi不能写为基本随机变量 ｛X｝的显示表达式，因此对每个变量进行敏度分析很难得到。利用响应面法，通过拟合解析表达式代替真实曲面从而将其应用到可靠性分析中［3］。对n个随机变量的情况，可写成

式中：a，bi，ci为表达式的待定系数。

从响应面的表达式看，如果有 n个基本随机变量，则有m=2n+1个待定系数［4-5］。

2.1梁元端面对轴弯曲失效

式中：Ri为第i个梁元对轴的弯曲抗力为局部坐标系下节点力向量为第i个梁元对于轴的塑性剖面模数。

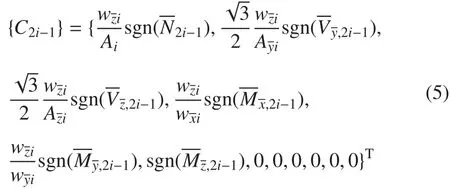
式中：sgn为符号函数；Ai为梁元截面积；为节点力；为第i个梁元沿方向的抗剪面积为第i个梁元绕轴的塑性扭转系数为第i个梁元对轴的塑性剖面模数

2.2板元屈服失效的功能函数

板元考虑屈服失效时的功能函数为

3　结构可靠度计算

对于舰体局部结构的第i个元件（梁或是板），其功能函数可写为［6-9］

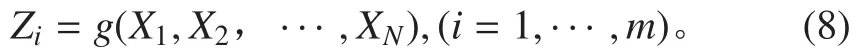
式中：｛X｝为基本随机变量向量，主要有外载荷，板元厚度；N为基本随机变量个数。

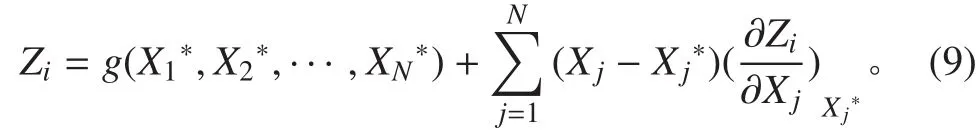
Zi并不能完全写为基本随机变量 ｛X｝的显示表达式，因此对每个变量的很难得到。然而，Zi可以写成部分基本随机变量（如强度和位移向量 ｛D｝的显示表达式，而 ｛D｝ 通过有限控制方程与基本随机变量相联系。

式（10）对 Xj求导，可得

对于系统可靠性，则采用分枝限界法寻找结构的失效模式，采用 PNET 法计算整个系统的可靠性［5］。

4　开口结构的可靠性计算结果

4.1结构元件可靠指标计算结果

根据上述理论编制的三维梁板元件结构可靠度FORTRAN 计算程序，计算了#211 肋位～#250 肋位舱段模型分别在中拱工况下的元可靠指标。

中拱工况下，元件可靠指标最低的5个梁单元和 5个板单元见表1和表2。

表1　中拱工况梁元可靠度列表Tab.1 Probability of girder element in hogging operating mode

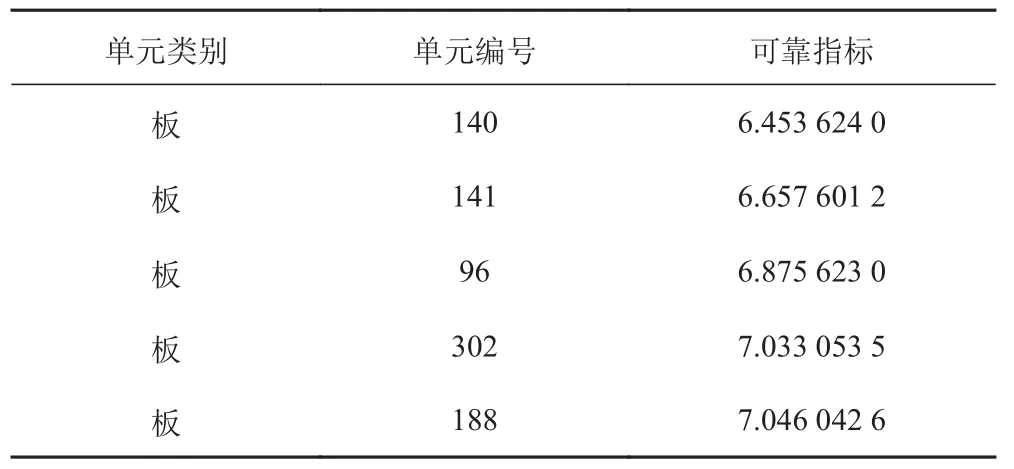
表2　中拱工况板元可靠度列表Tab.2 Probability of panel element in hogging operating mode

从表中可以看出，在梁板单元中，梁元的可靠指标要普遍低于板元的可靠指标。可靠指标较低的梁单元，均位于#241 肋位甲板大开口附近。

4.2结构系统可靠指标计算结果

利用结构系统可靠性的FORTRAN 程序，计算了中拱工况下#211 肋位～#250 肋位舱段结构系统的可靠性［9-11］。

通过分枝限界 Fortran 程序，在中拱工况下，找到了10个结构系统的主失效模式，失效模式和失效模式对应的失效路径见表3。

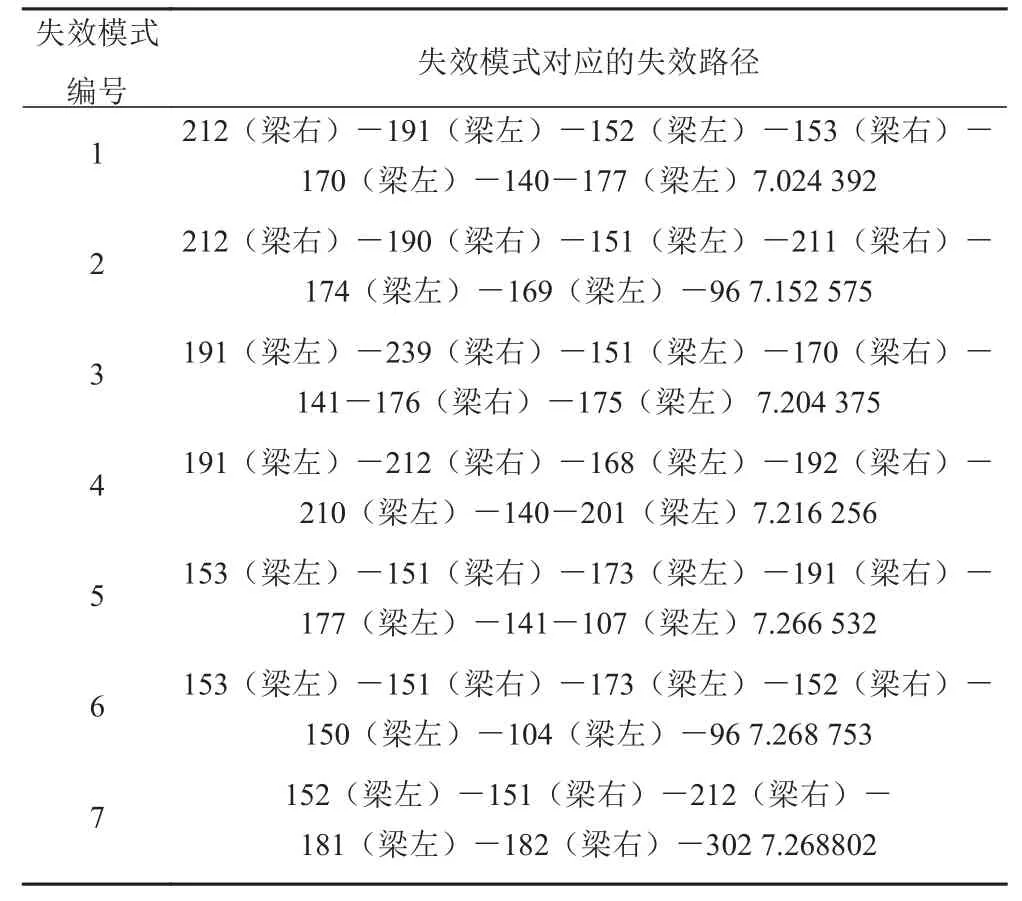
表3　中拱工况失效模式表Tab.3 The main damage path of panel element in hogging operating mode

根据表3中的结构系统主失效模式，由 PNET 法计算程序可计算得到中拱工况下，#211 肋位～#250 肋位局部结构系统的可靠指标及其失效概率，列于表4。

表4　＃211 肋位～＃250 肋位局部结构系统可靠指标Tab.4 211～250 rib local structure system reliability index

5　Ansys 可靠性分析结果

可靠性分析中，以载荷、材料的杨氏模量、材料的极限屈服强度为随机变量，均假定服从正态分布，集中载荷的变异系数为 0.2，舱段两端承受弯矩的变异系数为 0.2。材料的极限屈服强度取 440 MPa，变异系数0.08，杨氏模量的变异系数为 0.03。

通过敏度分析可以看出，最大应力对杨氏模量和材料的极限屈服强度不敏感。因此在响应面方程中只包含了与载荷有关的项，如图3所示。

从最危险点的取样历史（见图4）可以看出，应力最大值为 244.54 MPa，小于材料的极限屈服强度。开口结构的最大应力小于材料的极限屈服强度的概率pr约为 0.999 99（见图5），可靠性指标 β ＞ 4。

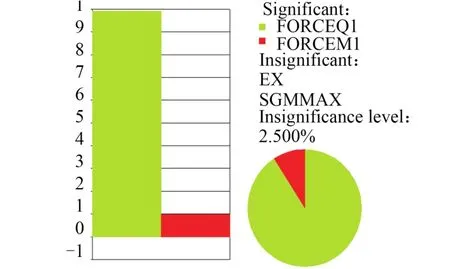
图2　最大应力对各随机变量的敏度分析Fig.2　Sensitivity analysis of the maximum stress to random variables

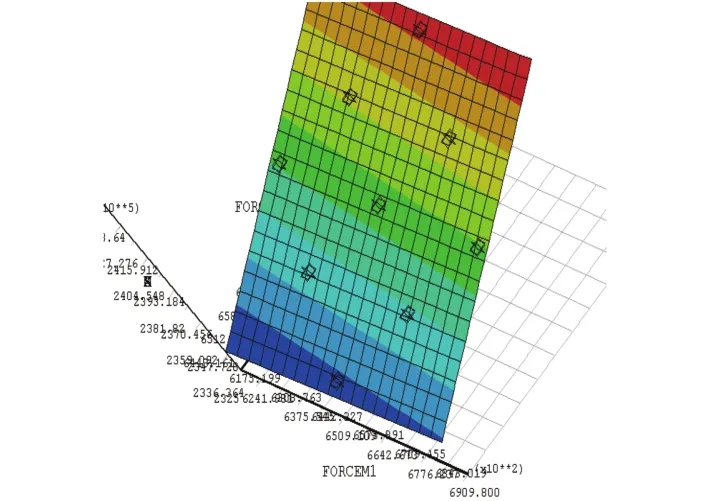
图3　最大应力对变量的响应面Fig.3　Response surface of maximum stress

图4　最危险点的取样历程Fig.4　sampling history of the most to random variables

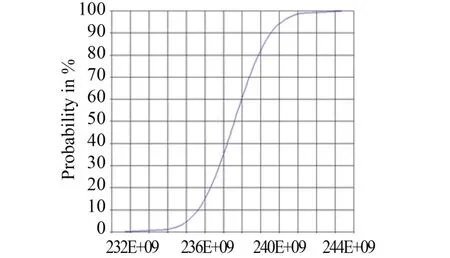
图5　最危险点的累积分布函数Fig.5　Cumulative distribution functions of the most dangerous point

6　结 语

本文分析了某型舰局部结构的梁元和板元在中拱工况下的元件的可靠指标，找到了局部结构中的薄弱位置。找到了局部结构系统在中拱工况下 10个主失效模式，并求得系统可靠指标及其失效概率。通过计算结果可以发现，主失效路径主要位于开口附近，说明开口对局部结构系统可靠度的影响比较大。数值计算表明，开口部位的可靠性指标较高，对舰的影响不大。在极限状态方程中，由于位移是随机量，并且不能用显式表达，故将一次二阶矩的可靠性指标迭代与随机有限元结合，给出了含有隐式变量的功能函数的求解方法，解决了杂交梁元和加筋板的可靠性问题。

利用大型有限元计算软件 Ansys中对某型舰船的开口结构进行可靠性分析。使用响应面法作为分析结构可靠性的基本方法，研究了结构的可靠性指标。通过分析可以看出，船体开口部位结构可靠指标较高，满足结构可靠性要求。利用随机有限元方法和 CAE 软件结合开展结构系统开展可靠性研究，避免了大型结构寻找实效模式的困难，使可靠性分析的效率得到极大提高。

［1］凌纯，周清华，杜留法.舰用减摇鳍加强结构的CAD/CAE一体化设计［J］.舰船科学与技术，2012，34（8）：60-63.LING Chun，ZHOU Qing-hua，DU Liu-fa.The CAD/CAE integrated design and analysis of naval ship fin stabilizer reinforced structure［J］.Ship Science and Technology，2012，34（8）：60-63.

［2］BUCHER C G，BOURGUND U.A fast and efficient response surface approach for structural reliability problems［J］.Structural Safety，1990，7（1）：57-66.

［3］武清玺，卓家寿.结构可靠度分析的变f序列响应面法及其应用［J］.河海大学学报，2001，29（2）：75-78.WU Qing-xi，ZHUO Jia-shou.A sequential response surface method with various f and its application to structural reliability analysis［J］.Journal of Hehai University，2001，29（2）：75-78.

［4］杨成永，张弥，白小亮.用于结构可靠度分析的多响应面法［J］.北方交通大学学报，2001，25（1）：1-4.YANG Cheng-yong，ZHANG Mi，BAI Xiao-liang.Multiple response surface method in analysis of structural reliability［J］.Journal of Northern Jiaotong University，2001，25（1）：1-4.

［5］谢永和，吴剑国，李俊来.船舶结构设计［M］.上海：上海交通大学出版社，2011.

［6］胡云昌，郭振邦.结构系统可靠性分析原理及应用［M］.天津：天津大学出版社，1992：6-7.

［7］严心池，华渊.基于随机有限元法的结构系统可靠性分析［J］.武汉理工大学学报，2010，32（9）：69-71，75.YAN Xin-chi，HUA Yuan.Structural system reliability analysis based on stochastic finite element method［J］.Journal of Wuhan University of Technology，2010，32（9）：69-71，75.

［8］安伟光.结构系统可靠性和基于可靠性的优化设计［M］.北京：国防工业出版社，1997.

［9］龙兵，安伟光，蔡荫林.基于随机有限元船舶空间结构系统可靠性分析［J］.哈尔滨工程大学学报，2002，23（3）：8-11.LONG Bing，AN Wei-guang，CAI Yin-lin.Reliability analysis for ship spatial structure based on SFEM［J］.Journal of Harbin Engineering University，2002，23（3）：8-11.

Probability simulation of opening structure in a naval ship

HUANG Jin-e，LIU Long-bo
（Naval Academy of Armament，Beijing 100073，China）

The girder and plane model of a naval ship is established based on the stochastic finite element of response surface and the theory of structure reliability.Adapted first-order second-moment methodadvanced branch-and-bound method and PNET method are used to do reliability analysis for the opening structure system.The reliability of the opening structure in the ship is analyzed on the combined loads.This method can avoid difficulty of looking for significant failure modes by using the stochastic finite element method and CAE software.

opening structure；stochastic finite element method；response surface；structural reliability

TB114.3

A

1672-7619（2016）07-0149-04

10.3404/j.issn.1672-7619.2016.07.033

2015-11-18；

2015-12-20

黄金娥（ 1975- ），女，硕士，工程师，主要从事舰船防护的研究。