堰塞体浸润线的Monte Carlo模拟

刘德伟 ，李连侠 ，廖华胜 ，罗树

（1.水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.Michigan State University, East Lansing,USA；3.西南电力设计院有限公司，四川 成都 610021）

堰塞体浸润线的Monte Carlo模拟

刘德伟1，李连侠1，廖华胜2，罗树火昆3

（1.水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.Michigan State University, East Lansing,USA；3.西南电力设计院有限公司，四川 成都 610021）

浸润线的高低对堰塞体的渗透稳定至关重要，而堰塞体材料渗透系数往往具有很强的随机性，如果采用确定性模型则不能准确地模拟实际的渗流场及浸润线位置。本文利用Monte Carlo方法在堰塞体材料渗透系数满足对数正态分布的条件下，对唐家山堰塞体渗流场进行了300次二维随机模拟。结果表明，受材料随机性的影响，水头场、浸润线分布及渗透坡降场等均呈现随机特性，但和渗透系数场的随机性并非简单的线性关系，水头方差空间变化特性较为明显，越往下游其值越大；对比确定性模型，随机性模型中出逸点的计算结果更具统计意义，对工程防护中有一定指导意义；由于受边界条件影响较小，堰体中间部位渗流特性基本满足正态分布；浸润线逸出点处受边界条件影响较大，逸出位置分布集中，不服从正态分布，其余部位浸润线位置高程随机过程基本服从正态分布。

渗流；堰塞体；Monte Carlo方法；浸润线；渗透系数

1 研究背景

2008年5月12 日，汶川大地震引发了34座大型堰塞湖和数以百计的小型堰塞湖，对下游地区人民的生命财产将构成巨大的威胁。堰塞体有不同于人工堆筑坝体的地方：堰塞体是由新鲜的、不均匀的、欠固结的滑坡土体堆积而成，级配较广，土体组成粒径从黏性颗粒到块石不等[1]。透水性强和弱的材料相互掺，造成渗透系数分布的非均质性。这种非均质性使得应用确定性方法处理非确定的堰塞湖渗流问题具有很大的局限性，很难客观地反映实际的渗流特性。

刘海峰等[2]以汶川地震中绵远河堰塞湖群排险工程为例，定性分析堰塞湖群溃决的风险影响因素；严祖文等[3]就根据既往的研究成果，主要阐述了堰塞湖天然坝坝体安全应急评估的基本方法和原则，基于唐家山堰塞体的岩体结构稳定性分析、宏观现象监控与地表位移监测，研究堰塞体的整体稳定性；崔银祥等[4]通过三维渗流计算评价堰塞体渗透稳定性，在进行稳定性评价时先评价坝体内水力坡度最大方向上格点的渗流稳定性，进而评价整个坝体的渗透稳定性。

从前人的研究成果来看，大多采用确定性模型进行模拟，对堰塞湖的材料特性对渗流影响的研究很少；很少考虑到堰塞体材料渗透系数具有随机性这一特点；对堰塞湖浸润线模拟较少，而浸润线的高低直接影响到堰塞湖的渗流稳定。而随机地下水模拟方法则考虑了介质的空间变异性和由此引起的因变量的不确定性，能够较为客观地反映现实规律[5]。Monte-Carlo方法就是一种使用随机样本技术，通过计算机随机模拟而获得问题的近似解的方法，它特别适用于解具有一定概率分布的问题。本文依据现有堰塞湖资料，建立适当的概化模型，采用自编的饱和-非饱和渗流计算程序[6]，并引入Monte Carlo模拟进行二维立面渗流数值模拟。

2 计算模型及参数的确定

目前，已经有许多随机数值方法用于分析地下水输运问题方法，包括Monte-Carlo方法、扰动方法及基于Taylor展开的一次二阶矩法等[7]。其中，Monte-Carlo方法使用最为广泛。

2.1 随机地下水模型的建立

二维饱和/非饱和渗流的基本方程[8]如下：

式中：kmh m为渗透系数，是压力水头h的函数，h= H-y；H为水头；x为水平方向坐标；y为垂向坐标；n为土体孔隙度；c′mh m为相对饱和度；λ是饱和度，λ=兹/n，θ为体积含水率；SS为贮水率。

本文模拟堰塞体内稳定渗流的浸润线，此时方程（1）的右边项为零，求解时只需要给定k-h的关系即土水特征曲线，堰塞体两种材料土水特征曲线采用Van Genuchten模型。

国内外学者对于含水层的渗透系数做出了大量研究[5，6，9]，发现无论是在微观颗粒还是宏观区域来讲k值都具有随机性。Freeze[10]统计了大量饱和渗透系数资料，结果表明，饱和渗透系数可以用对数正态分布来描述，其概率密度分布如下：

式中：滋为饱和渗透系数均值；滓为饱和渗透系数标准差。

2.2 模型尺寸边界条件的确定

如图1所示，坝体底宽为堰塞坝顺河向长度为803.4 m，坝顶高程为759.55 m，坝底高程为669.55 m。坝体主体为厚度90 m的碎裂岩。坝基为苦竹坝库区沉积的8 m厚度含泥粉细砂，下伏风化基岩。上游坝坡被滑坡挤压隆起的含泥粉细砂覆盖，其坝顶高程为735 m。上游坝坡坡度为20°。下游坝坡分为三段：上部坡比为 1∶0.7，坡高为50 m；下部坡比为 1∶0.5，坡高为 20 m；中部为缓坡，坡比为 1∶2.5。

由于模型底部粉细砂下卧风化基岩，边界作为不透水设置。顺河向两侧为自由临空面，上游为定水头边界（第一类边界），下游自由面边界，堰塞体脚处为定水头边界。据堰塞体工程地质评价以及坝体组成物质和经验判断，模型中粉细砂和碎裂岩饱和渗透系数均值分别取8.64×10-2m/d和 8.64 m/d，Van Genuchten模型（式（2））中参数m均取1.58，参数α取0.001 7 m-1，其相应的允许坡降分别为0.1和0.6。

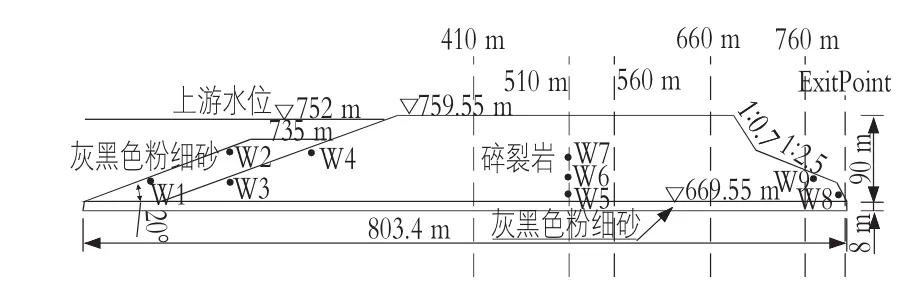
图1 唐家山堰塞体二维模型

在对比不同尺度的计算结果的情况下，取均值K1区域的相关尺度为2 000，取均值K2区域的相关尺度为1 000。Freeze曾系统地分析过一些含水量，认为砂砾石含水层方差滓=0.92；淤泥层方差滓=2.14。本文在比较分析后，取方差为滓=3。为了对Monte-Carlo方法随机计算过程进行检验，在堰塞体内部加入监测井（见图1）。监测井不为源汇项，不影响计算结果，仅为结果输出设立。

3 Monte-Carlo模拟结果分析

3.1 随机过程检验

为检验Monte-Carlo方法样本个数的统计代表性，共进行了300次样本模拟计算。图2和图3为不同监测井不同样本容量统计计算得到的对数渗透系数和水头的样本均值。由图2，3可见，随着样本容量的增加，样本均值快速趋近于定值。说明样本容量300可到统计所需样本容量的要求。

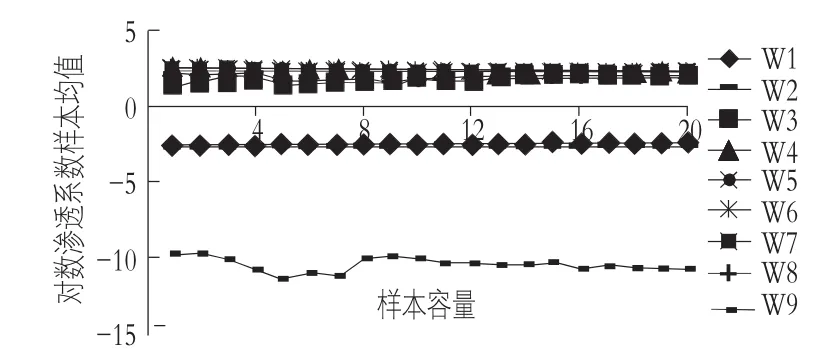
图2 不同井监测的对数渗透系数的样本均值

图3 各监测井水头均值

本文视饱和渗透系数随机场为标准对数正态分布场，计算是否能保持应有的统计特性直接影响到随机场模拟结果的质量。下面选取编号为W5，W6，W7，横坐标都为510 m，纵坐标差值为20 m的3个监测井考察统计性质。

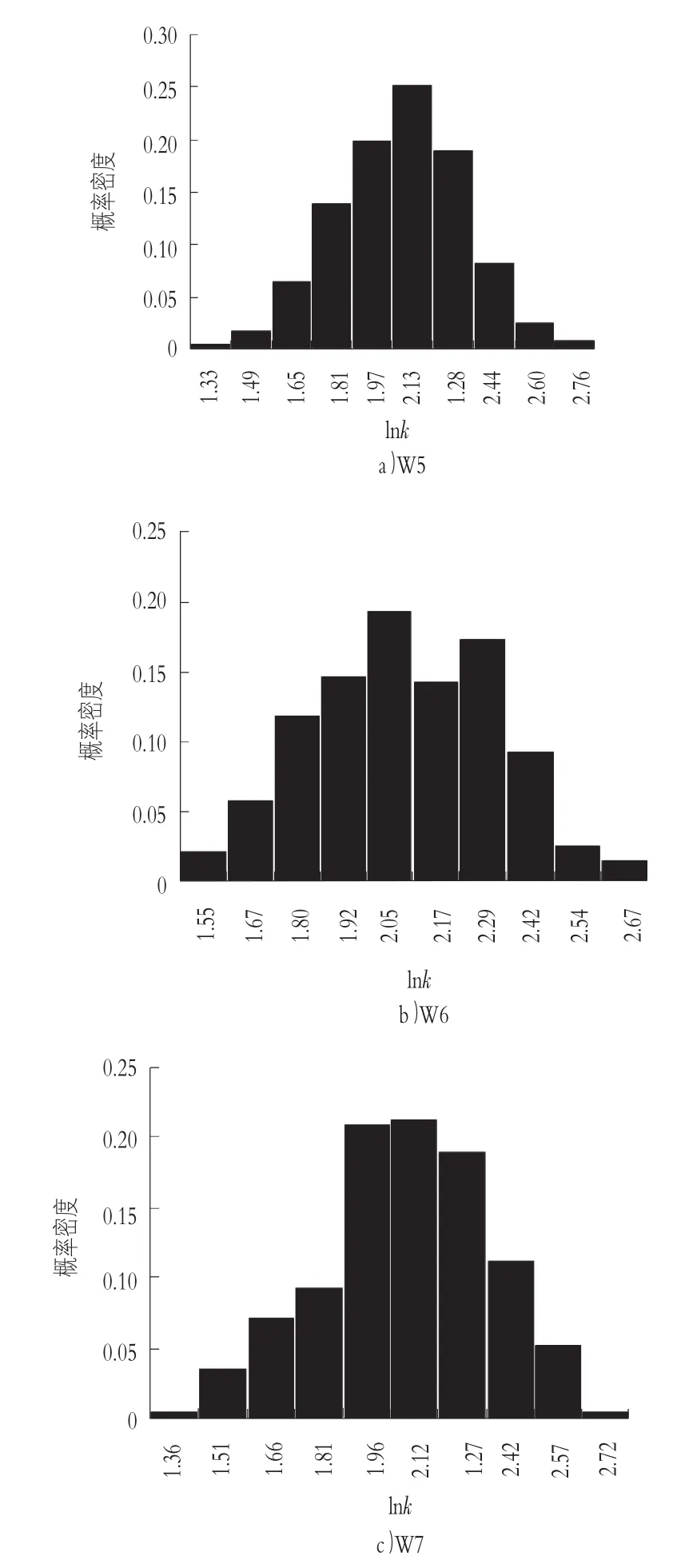
图4 对数饱和渗透系数概率密度分布直方图

从图4对数饱和渗透系数概率密度分布直方图看出，编号为W5，W6，W7等3个井的对数饱和渗透系数概率密度基本上关于lnk1=2.15，lnk2= 2.4，lnk3=2.16对称分布，符合正态分布特征。

从图5水头概率分布直方图看出，水头概率密度基本上关于H水头=730.6 m对称分布，符合正态分布特征。

3.2 典型样本计算结果分析

由饱和渗透系数KS的随机性，可以推断计算结果的随机性，选取样本号为50和250的两个不同随机样本计算所得的水头等值线分布、渗流速度分布、渗透坡降进行结果分析。

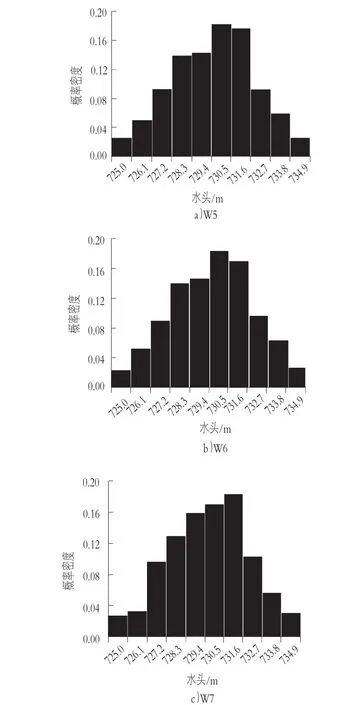
图5 水头概率密度分布直方图

图6对比不同随机场的计算结果，发现水头分布沿程降低，降低幅度基本相同。受材料随机性的影响，各个样本之间等水头线分布不尽相同，等水头线在垂直方向有扭曲现象。

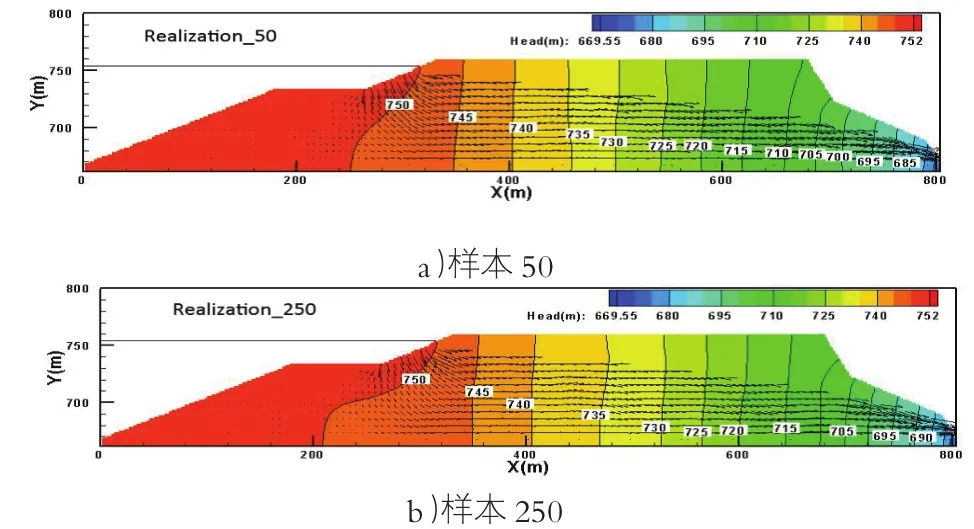
图6 不同随机场的水头等值线及渗透速度分布图

图7 不同随机场的渗透坡降等值线计算结果

图8 确定性模型渗透坡降等值线图

由图7堰塞体内渗透坡降等值线分布可以更明显地看出材料随机性对渗流的影响。各个随机场计算的渗透坡降分布范围大致相同，但是等值线几乎不同，渗透坡降等值线破碎，不连续，随机特性明显，堰塞体内最大渗透坡降均未超过允许坡降。对比图8确定性模型渗透坡降等值线图，可以看出随机性模型中渗透坡降大于0.2的区域相对较大，不利于堰体的渗流稳定。

3.3 浸润线计算结果分析

为了研究分布规律，在本文的Monte Carlo数值模型中选取 X=410，510，560，660，760 m 等 5 个断面及逸出点的浸润线位置作为分析对象。各个断面的统计结果如表1所示。

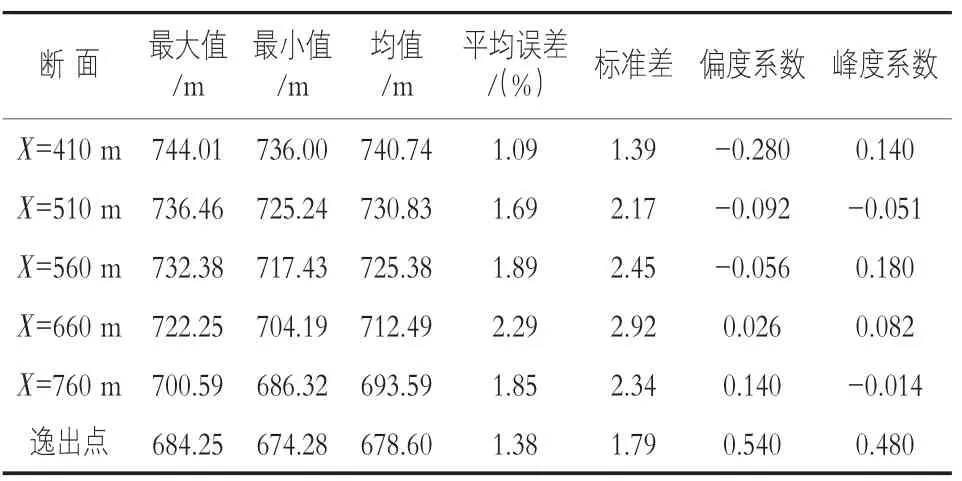
表1 不同断面浸润线高程统计规律计算表

图9为300个样本的浸润线分布，图中粗实线为采用确定性模型（渗透系数取均值）得到的浸润线。

由图9可以看出，受材料随机性影响，浸润线分布随样本不同而不同，随位置向下游移动浸润线分布逐渐分散，大约在X=650 m断面处分散程度达到最大，由于受下游坝坡边界影响，再往下游浸润线出现聚拢现象。

图9 浸润线分布图

现对300个样本的逸出点高程做出统计结果见图10。

图10 逸出点高程分布直方图

逸出点高程分布在674.28~684.25 m之间。其中有85.7%的逸出点高程分布在676.04~680.15 m之间。图9黑色线为采用确定性模型计算的浸润线，其出逸点高程为680.8 m，高于随机性模型的浸润线的平均高程678.603 m。说明采用均值的K进行计算得到的结果与采用随机K场进行多样本模拟后得到的结果的均值并非一致，随机性模型中出逸点的计算结果更具统计意义，对在工程防护中拟订防护措施和范围具有明确的指导意义，减少盲目性。

4 结 论

1）Monte-Carlo模拟结果表明，受材料随机性的影响，水头场、浸润线分布及渗透坡降场等均呈现随机特性，不同样本之间水头分布不尽相同，水头均值场与确定性模型计算结果非常接近；水头方差场与渗透系数K的方差场的关系并非简单的线性关系：水头方差空间变化特性较为明显，越往下游其值越大，说明最大的不确定性发生在堰塞体下游部位，其变化程度更为激烈。

2）采用均值的渗透系数K进行计算得到的结果与采用随机渗透系数场进行多样本模拟后得到的结果的均值并非一致，随机性模型中出逸点的计算结果更具统计意义，对在工程防护中拟订防护措施和范围具有更明确的指导意义，减少盲目性。

3）典型采样位置的模拟结果表明，水头标准差在上游侧均较小，随位置向下游移动，由于下游逸出点的非线性，其值进一步增大，使得逸出点附近水头的不确定性程度增加，位于堰体中部的监测点的概率密度分布更接近正态分布，其余各处由于受边界条件影响其分布均不同程度偏离正态分布。说明输入参数的正态特性并不能保证输出结果的正态分布特性，输入和输出之间的非线性关系和边界条件的影响会破坏这种概率分布的线性传递。

［1］刘海峰，周宏伟.地震堰塞湖风险影响评价定性分析［J］.东北水利水电，2013（2）55—57.

［2］李守定，李晓，张军，赫建明，李世海，汪阳春.唐家山滑坡成因机制与堰塞坝整体稳定性研究［J］.岩石力学与工程学报，2010，29（S1）：2908—2915.

［3］严祖文，魏迎奇，蔡红.堰塞坝渗透稳定性评估［J］.长江科学院院报，2009，6（10）：122—125.

［4］崔银祥,聂德新，等.通过三维渗流计算评价某滑坡坝渗透稳定性［J］.水土保持研究，2005，12（2）：97—100.

［5］王亚军，张我华，陈合龙.长江堤防三维随机渗流场研究［J］.岩石力学与工程学报，2007，26（09）：1824—1824.

［6］廖华胜，李连侠，LI Shu-guang.地下水非平稳随机模型及空间变异性与非均匀性相互关系研究的展望［J］.水利学报，2004，35（10）：13—21.

［7］孙莹洁，等.滑坡体渗流场与库水位波动响应关系研究［J］.人民长江，2014，45（7）：66—69.

［8］ SUDICKY E A.A natural gradient experiment on solute transport in a sand aquifer:spatial variability of hydraulic conductivity and its role in the dispersion process［J］.Water Research，1986，22（13）：2017—2029.

［9］ K.Binder,D.W.Heerman.MonteCarloSimulationinStatistical Physics An Introduction［M］.New York:Springer verlag, Berlin Heideberg，2010，5th ed.

［10］ R.A.Freeze.A stochastic-conceptual analysis of onedimensional groundwater flow in nonuniform homogeneous media.Water Resource Research，1975，11（5）：725—741.

TV131.61；P315.9

A

1002－0624（2016）04－0043－05

国家自然科学青年基金（51209154）。

李连侠，博士，副教授，主要从事工程水力学和地下水研究。

2015-10-10