基于核回归修正的上采样相位相关精确运动估计算法
余应淮 谢仕义 梅其祥


摘要:针对亚像素运动矢量的精确估计问题,提出一种基于核回归修正的上采样相位相关精确运动估计算法。首先,使用矩阵相乘离散傅里叶变换方法快速计算上采样相位相关曲面,并通过检测其峰值坐标实现运动矢量的亚像素级初始估计;其次,在上采样相位相关曲面上,采用核回归方法对以初始估计值为中心的邻域进行拟合;最后,检测核回归拟合函数的峰值坐标,并以此坐标对初始估计值进行修正,从而实现任意精度级别的精确运动估计。与二次函数拟合(QuadFit)、线性拟合(LinFit)、Sinc拟合(SincFit)、局部质心(LCM)、频域上采样(Upsamp)等算法进行仿真对比,在无噪声污染的情况下,所提算法的平均估计误差为0.0070,运动估计的准确度提高了64%以上;而在有噪声污染的情况下,所提出的算法的平均估计误差为0.0204,运动估计的准确度提高了47%以上。实验结果表明,所提算法不仅能够有效地提高运动估计的精确性,而且具有良好的抗噪性。
关键词:运动估计;相位相关;上采样;矩阵相乘;核回归
中图分类号:TP391.41
文献标志码:A
0引言
相位相关法作为一种传统的频域运动估计技术,最早由Kuglin[1]在1975年提出。该方法通过在频域空间计算相位相关曲面的单一脉冲的位置直接得到图像之间的运动矢量,具有较低的时空复杂度;同时,该方法只利用了运动图像之间互功率谱的相位信息,降低了对图像内容的依赖性,且对光照变化相对不敏感,具有较高鲁棒性和抗噪性,因此被广泛应用于图像配准与超分辨率重建[2-4]、图像拼接[5-6]、指纹与虹膜识别[7-8]、目标检测[9-10]、立体视觉与视频编码[11-15]等。另一方面,基本的相位相关算法仅能实现整像素级别的运动估计,其估计结果的精度直接影响着运动补偿误差,是上述应用需要解决的关键问题。为了实现亚像素级别的精确运动估计,众多研究人员对上述的基本相位相关算法进行了扩展,其具有代表性的改进方法主要有以下几类:二次函数拟合(Quadratic function Fitting,QuadFit)、线性拟合(Linear Fitting,LinFit)、Sinc拟合(Sinc Fitting,SincFit)、局部质心(Local Center of Mass,LCM)、频域上采样(Upsampling in the frequency domain,Upsamp)。
其中,QuadFit方法[16-18]作为一种常规的改进方法,其核心思想是应用基本的相位相关算法获得运动矢量的整像素级初始估计,并采用二次多项式对以初始估计值为中心的邻域进行拟合,最后通过检测拟合函数的峰值坐标得到初始估计的亚像素级修正值;尽管该方法实现了亚像素级的运动估计,且具备良好的抗噪性,但估计结果对于邻域点的选择较为敏感。LinFit方法[19-20]则通过对运动图像间的归一化互功率谱的相位进行解缠,并采用一个线性函数对解缠结果进行拟合,从而实现亚像素级的运动估计;在理想的情况下,该方法能够得到较好的估计结果,但对噪声影响的鲁棒性较低,且解缠过程中所引入的误差容易对估计结果的准确性造成影响。而SincFit方法[21]采用基于泰勒级数展开式的sinc函数近似地表示运动图像间的相位相关函数,在一定程度上提高了运动估计结果的精确度,但仍然受限于sinc函数与相位相关函数之间的残差。LCM方法[22-23]应用了亚像素级的运动将导致相位相关函数的主峰能量在一定程度上分散于邻近点的思想,在相位相关曲面上计算以主峰值为中心的邻域的质心值,并以此值对主峰值坐标进行修正,最终得到亚像素级的运动矢量估计值;和上述其他方法一样,由于其主峰值坐标为整像素级,容易导致后续的亚像素级修正值的计算发生较大偏差,即估计结果可能存在整像素级误差。Upsamp方法[24]尽管可以避免整像素级初始估计所产生的误差影响,但该方法仅能实现上采样因子所限定的估计精度,即运动矢量估计值的精度为1/n像素,仍然无法解决任意精度级别的亚像素运动估计问题,且算法的时空复杂度与估计精度成正比。
为实现任意精度亚像素运动矢量的估计,本文探讨一种基于核回归修正的相位相关精确运动估计算法。首先,引入矩阵相乘离散傅里叶变换快速计算运动图像间的上采样相位相关函数,通过检测其峰值坐标获得运动矢量的亚像素级初始估计,以此将估计误差缩小在1/n像素级的范围内,同时降低算法的时空复杂度;其次,在上采样相位相关曲面上,采用核回归方法对以初始估计值为中心的3×3邻域进行拟合;最后,以核回归拟合函数的峰值坐标对亚像素级的初始估计值进行修正,从而实现任意精度级别的精确运动估计。实验结果表明,所提出的算法不仅具有良好的抗噪性,而且能够有效地提高运动估计的精确性。
1整像素级运动估计的基本相位相关法
运用基本的相位相关法进行运动估计,其核心思想是傅里叶变换的平移性质,即图像在空域中的相对运动只引起频域中相位的线性变化,且频谱的幅值不发生变化。算法的基本步骤是在频域中计算发生相对运动的两幅图像之间的归一化互功率谱,并对其执行傅里叶逆变换得到相位相关函数,最后通过检测相位相关函数的峰值坐标得到整像素级的运动矢量估计值,具体如下:
由式(5)可见,运动图像间的相位相关函数由一个脉冲函数构成,通过检测其峰值坐标即可得到运动矢量的整像素级估计值。
2基于核回归修正的上采样相位相关法
在实际的应用场景中,由于图像之间的相对运动是连续的,而采用第1章介绍的基本相位相关法进行运动估计,仅能得到运动矢量的整像素级估计值,这并不符合真实的运动情况。为了实现任意精度的亚像素运动精确估计,本章首先采用矩阵相乘离散傅里叶变换方法快速计算运动图像间的n倍上采样相位相关函数,以此实现亚像素级的初始运动估计;然后应用核回归方法对初始估计进行精确修正,从而得到任意精度的运动矢量精确估计值。
2.1运动矢量的亚像素初始估计值的快速计算
为了得到运动图像间的n倍上采样相位相关函数cn(x,y),常规的实现方法是在频域中采用n倍零填充对式(1)所示的归一化互功率谱进行2维对称扩展,得到n倍上采样的归一化互功率谱Cn(u,v),然后对其执行傅里叶逆变换。其中,上采样因子n的取值不仅决定了运动估计的精确度,同时也直接影响着算法的时空复杂度。例如,对于大小为1024×1024的运动图像序列,若要实现精度为1/10像素的亚像素运动估计,则采用零填充方法计算10倍上采样的相位相关函数,需要执行10240×10240次逆傅里叶变换的计算量以及相应的存储空间。因此,为了提高算法的执行效率,本文应用矩阵相乘离散傅里叶变换方法[24-26]快速计算上述精度为1/n像素的亚像素初始估计值。
由式(2)可得到运动图像f(x,y)与参考图像g(x,y)之间的相位相关函数的共轭形式c*(x,y),如式(6)所示:
2.2初始估计值的核回归精确修正
由于上采样方法仅能获得上采样因子所限定的1/n像素级的估计结果,且上采样因子选取也可能使相位相关函数的峰值坐标产生偏移,会直接影响着运动估计的精确性。核回归作为一种非线性方法,已经在图像处理的多个领域得到了应用[27-29]。为实现任意精度的运动矢量精确估计,本节引入核回归拟合方法对2.1节所得到的初始估计值(dxn,dyn)进行精确修正。其基本思想是:在n倍上采样相位相关曲面上,采用核回归函数拟合以初始估计值为中心的3×3邻域,然后以拟合曲面的峰值坐标对初始估计值进行精确修正。
假设由上述3×3邻域内的相关值拟合的函数r(x)所属空间为再生核Hilbert空间。定义rm为该邻域内各相关值所构成的列向量,m为相关值的个数,且第i个相关值对应的核函数如下:
3实验与结果分析
通过三组实验将本文算法与新近相关文献的代表性算法进行比较分析,包括文献[18]的QuadFit算法、文献[20]的LinFit算法、文献[21]的SincFit算法、文献[23]的LCM算法和文献[24]的Upsamp算法,以此检验本文算法的精确性、抗噪性以及有效性。其中,实验图像包括人工生成相对运动的无噪图像序列和相应的加噪图像序列,以及实际拍摄的视频分区
图像序列。实验环境配置如下:Intel CPU(i5-2430M,2.40GHz)、8.0GB内存、64位的Windows7操作系统。
在实验中,为获得高精度的运动估计结果,将Upsamp算法的上采样因子n取值为10000,而本文算法的上采样因子则取值为10;同时,为便于估计结果的比较,将本文算法以及QuadFit、LinFit、SincFit、LCM等算法的估计结果经四舍五入仅保留4位小数。对于估计结果的准确性,本文采用估计结果(dx,dy)与实际运动矢量(Dx,Dy)之间的均方根误差(Root Mean Square Error,RMSE)作为衡量指标,其计算方法如式(21)所示:
3.1无噪声影响的运动估计性能比较
本节实验采用1组人工生成亚像素级相对运动的无噪图像序列Einstein作为实验图像,如图1所示。其中包含1帧参考图像和7帧运动图像,图像大小为40×40;各帧运动图像的运动方向随机生成,相应的运动矢量为正负10之间的任意随机数,如表1所示。
各对比算法的运动估计结果如表2、图2所示。通过对比可知,表2所示的各种算法的运动矢量估计值均比较接近表1的各项实际运动矢量,但各种算法的估计结果的精确性有所不同;其中,本文算法的估计结果的平均RMSE为0.0070,而QuadFit、LinFit、SincFit、LCM、Upsamp等算法的平均RMSE则分别为0.0333、0.0195、0.0279、0.0616、0.0399,本文算法的运动估计精确性明显高于上述所比较算法,其估计结果更加接近实际的运动矢量。在算法的执行效率方面,Upsamp算法由于本身固有的缺陷,其运行时间最长,是其他
算法的100倍左右;而本文算法由于采用低倍数上采样因子,同时引入矩阵相乘离散傅里叶变换方法快速计算上采样相位相关函数,有效地减少了算法的执行时间,尽管稍高于QuadFit、LinFit、SincFit、LCM等算法,但仍然与后者保持相同的数量级,具有较高的执行效率。
3.2噪声影响下的运动估计性能比较
本节对3.1节实验所用的实验图像分别叠加信噪比为10dB的随机噪声,并进行实验对比,以此检验本文算法在噪声影响下的运动估计性能,实验结果如表3、图3所示。
分析表3所示的运动矢量估计结果可知,在噪声污染的影响下,本文算法以及QuadFit、SincFit、LCM、Upsamp等算法的估计结果的准确性虽有一定程度的降低,但都表现出良好的抗噪性能,其运动矢量的估计值仍然接近表1所示的实际运动矢量;而LinFit算法对噪声影响则较为敏感,其估计结果较明显地偏离实际的运动矢量。
同时,由图3所示的运动估计误差比较可知,相对于无噪声污染的图像序列而言,本文算法以及上述所比较算法的估计误差RMSE都有一定程度的提高。其中,本文算法对第4帧运动图像的估计误差RMSE为0.0289,稍高于Upsamp算法的0.0244;除此之外,本文算法对其余各帧运动图像的估计误差RMSE均明显低于QuadFit、LinFit、SincFit、LCM、Upsamp等算法。本文算法及上述所比较算法的估计结果的平均RMSE分别为0.0204、0.0579、0.0943、0.0461、0.0775、0.0388,由此可知在噪声影响下,本文算法对运动矢量的估计精确度仍然高于上述所比较算法。
3.3真实应用场景下的运动估计性能比较
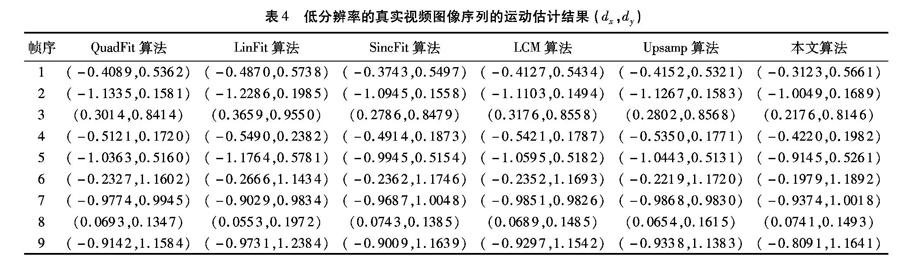
图像超分辨率重建技术利用图像序列中帧与帧之间的微小差异,利用一系列质量较差、分辨率较低的图像重建质量更好、空间分辨率更高的图像,而精确的运动估计则是成功实现超分辨率重建的关键步骤。本节实验采用一段真实的低分辨率视频的车牌区域截图作为实验图像序列,包含1帧参考图像和9帧运动图像,图像大小为29×27,如图4所示。通过本文所提出的算法对其进行运动估计,并使用估计结果进行图像配准,最后采用双三次插值方法实现图像的超分辨率重建,以此进一步检验本文算法的有效性。其中,各种算法的运动估计结果如表4所示,相应的3倍超分辨率重建结果则如图5所示。
分析表4所示的运动矢量估计结果可知,尽管无法比较估计结果与真实运动矢量的接近程度,但本文算法及所比较算法的估计结果的方向与实验图像序列中各帧运动图像的实际运动方向相符合。同时,通过对比图5所示的超分辨率重建结果可知,采用表4所示的运动矢量估计结果对低分辨率实验图像序列进行配准,并在此基础上采用双三次插值进行超分辨率重建均能够有效地改善原图像的质量,从视觉上较好地识别出图中的车牌号码。其中,采用本文算法进行运动估计的超分辨率重建结果图像的质量与SincFit算法相当,且明显优于其他算法;QuadFit、LCM、Upsamp等算法相应的超分辨率重建结果图像均存在轻微的锯齿效应和模糊,而LinFit算法相应的超分辨率重建结果图像的锯齿效应则较为明显。可见,本文算法能够有效地应用于亚像素级的精确运动估计。
4结语
针对亚像素级的精确运动估计问题,本文提出了一种基于核回归修正的上采样相位相关算法。首先,采用了矩阵相乘离散傅里叶变换快速计算上采样相位相关函数,通过检测该上采样函数的峰值坐标获得运动矢量的亚像素级初始估计值,有效地降低了整像素级初始估计所产生的误差影响,同时避免了传统上采样算法的高时空复杂度问题,提高了算法的执行效率。其次,引入了核回归拟合方法计算亚像素级初始估计的精确修正值,实现了任意精度级别的精确运动估计。实验结果表明,所提算法不仅能够有效地提高运动估计的精确性,而且对噪声影响具有良好的鲁棒性;但本文算法仍未解决缩放尺度、旋转角度等运动参数的估计问题,如何将仿射变换模型与本文算法相结合,进一步提高算法适用性是后续研究的重点。
参考文献:
[1]KUGLIN C D. The phase correlation image alignment method [C]// Proceedings of the 1975 IEEE International Conference on Cybernetics and Society. Piscataway, NJ: IEEE, 1975: 163-165.
[2]ITO K, NIKAIDO A, AOKI T, et al. A dental radiograph recognition system using phase-only correlation for human identification [J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2008, E91-A(1): 298-305.
[3]LEPRINCE S, BARBOT S, AYOUB F, et al. Automatic and precise orthorectification, coregistration, and subpixel correlation of satellite images, application to ground deformation measurements [J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(6): 1529-1558.
[4]LI X. An improved two-stage image registration algorithm for super-resolution [J]. IEEJ Transactions on Electrical and Electronic Engineering, 2014, 9(4): 415-420.
[5]KIM D-H, YOON Y-I, CHOI J-S. An efficient method to build panoramic image mosaics [J]. Pattern Recognition Letters, 2003, 24(14): 2421-2429.
[6]ZHANG J, WANG C-S, LIAO W-L. An image mosaics algorithm based on improved phase correlation [C]// ESIAT 09: Proceedings of the 2009 International Conference on Environmental Science and Information Application Technology. Washington, DC: IEEE Computer Society, 2009: 383-386.
[7]ITO K, NAKAJIMA H, KOBAYASHI K, et al. A fingerprint matching algorithm using phase-only correlation [J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2004, E87-A(3): 682-691.
[8]MIYAZAWA K, ITO K, AOKI T, et al. An effective approach for iris recognition using phase-based image matching [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(10): 1741-1756.
[9]YOKOYA N, MIYAMURA N, IWASAKI A. Detection and correction of spectral and spatial misregistrations for hyperspectral data using phase correlation method [J]. Applied Optics, 2010, 49(24): 4568-4575.
[10]MAY K, KROUGLICOF N. Moving target detection for sense and avoid using regional phase correlation [C]// ICRA 2013: Proceedings of the 2013 IEEE International Conference on Robotics and Automation. Piscataway, NJ: IEEE, 2013: 4767-4772.
[11]TAKITA K, MUQUIT M, AOKI T, et al. A sub-pixel correspondence search technique for computer vision applications [J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2004, E87-A (8): 1913-1923.
[12]OGURI T, IKEHARA M, NGUYEN T. 3D cube video coding using phase correlation motion estimation [J]. Electronics and Communications in Japan (Part Ⅲ: Fundamental Electronic Science), 2006, 89(5): 32-38.
[13]PAUL M, LIN W, LAU C T, et al. Direct intermode selection for H.264 video coding using phase correlation [J]. IEEE Transactions on Image Processing, 2011, 20(2): 461-473.
[14]ALBA A, ARCE-SANTANA E, AGUILAR-PONCE R M, et al. Phase-correlation guided area matching for realtime vision and video encoding [J]. Journal of Real-Time Image Processing, 2012, 9(4): 621-633.
[15]PODDER P K, PAUL M, MURSHED M, et al. Fast intermode selection for HEVC video coding using phase correlation [C]// DICTA 2014: Proceedings of the 2014 International Conference on Digital Image Computing: Techniques and Applications. Piscataway, NJ: IEEE, 2015: 1-8.
[16]ABDOU I E. Practical approach to the registration of multiple frames of video images [C]// Proceedings of the Visual Communications and Image Processing 99, SPIE 3563. Bellingham, WA: SPIE, 1999: 371-382.
[17]SHIMIZU M, OKUTOMI M. Sub-pixel estimation error cancellation on area-based matching [J]. International Journal of Computer Vision, 2005, 63(3): 207-224.
[18]ARGYRIOU V, VLACHOS T. A study of sub-pixel motion estimation using phase correlation [C]// BMVC 2006: Proceedings of the 2006 17th British Machine Vision Conference. Edinburgh: British Machine Vision Association, 2006: 387-396.
[19]HOGE W S. A subspace identification extension to the phase correlation method [J]. IEEE Transactions on Medical Imaging, 2003, 22(2): 277-280.
[20]TONG X, YE Z, XU Y, et al. A novel subpixel phase correlation method using singular value decomposition and unified random sample consensus [J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(8): 4143-4156.
[21]YU H, CHEN F-S, ZHANG Z-J, et al. A subpixel motion estimation approach based on the phase correlation [C]// OIMT II: Proceedings of the 2012 Optoelectronic Imaging and Multimedia Technology Ⅱ, SPIE 8558. Bellingham, WA: SPIE, 2012: 85580Y.
[22]FOROOSH H, ZERUBIA J B, BERTHOD M. Extension of phase correlation to subpixel registration [J]. IEEE Transactions on Image Processing, 2002, 11(3): 188-200.
[23]OUSGUINE S, ESSANOUNI F, ESSANOUNI L, et al. Motion estimation of aliased images using the phase correlation [C]// INTECH 2012: Proceedings of the 2nd International Conference on Innovative Computing Technology. Washington, DC: IEEE Computer Society, 2012: 170-173.
[24]GUIZAR-SICAIROS M, THURMAN S T, FIENUP J R. Efficient subpixel image registration algorithms [J]. Optics Letters, 2008, 33(2): 156-158.
[25]SOUMMER R, PUEYO L, SIVARAMAKRISHNAN A, et al. Fast computation of Lyot-style coronagraph propagation [J]. Optics Express, 2007, 15(24): 15935-15951.
[26]余应淮,王锦荣.高精度亚像素全局运动估计的上采样梯度互相关算法[J].中国图象图形学报,2012,17(12):1492-1499.(YU Y H, WANG J R. High accuracy sub-pixel global motion estimation based on upsampled gradient cross-correlation algorithm[J]. Journal of Image and Graphics, 2012, 17(12): 1492-1499.)
[27]TAKEDA H, FARSIU S, MILANFAR P. Kernel regression for image processing and reconstruction [J]. IEEE Transactions on Image Processing, 2007, 16(2): 349-366.
[28]LIU B, LIAO X. Image denoising and magnification via kernel fitting and modified SVD [C]// IAS 2009: Proceedings of the 5th International Conference on Information Assurance and Security. Washington, DC: IEEE Computer Society, 2009: 521-524.
[29]LIU B-Y, WU W-Y, CHEN X-W. Kernel fitting for image segmentation [C]// ICMLC 2008: Proceedings of the 7th International Conference on Machine Learning and Cybernetics. Washington, DC: IEEE Computer Society, 2008, 5: 2914-2917.
[30]LIU B, ZHANG J. An adaptively trained kernel-based nonlinear representor for handwritten digit classification [J]. Journal of Electronics (China), 2006, 23(3): 379-383.

