基于智能跳频的短波无线接入网动态频谱分配算法

段瑞杰　姚富强　李永贵　郭鹏程

摘要：针对现有短波无线接入网的固定式频谱分配方法难以满足使用智能跳频技术新要求的问题，分析智能跳频短波无线接入网的通信需求，提出智能跳频短波无线接入网的动态频谱分配策略及算法。首先将各机动用户和接入基站看作一子网；然后将对各子网的频谱分配建模为基于图着色理论的智能跳频短波无线接入网频谱分配模型；最后结合通信需求提出分配策略和算法，完成频谱分配并进行了仿真分析。结果表明，这些频谱分配策略及算法以不同的目标进行频谱分配，能够有效支撑智能跳频技术在短波无线接入网中的应用，与固定式频谱分配方法的定频通信相比，在网络效益、子网满意度、网络公平性、网络支持用户数和频谱利用率等方面均有明显提升，同时能有效降低互扰率。

关键词：短波无线接入网；智能跳频；非对称频谱配置；固定式频谱分配方法；图着色理论；动态频谱分配

中图分类号：TN915

文献标志码：A

0引言

短波通信组网运用将有效提高短波用户业务传输的有效性，增加业务传输种类，提高业务传输能力以及网络抗干扰能力，能组成不同层次的指挥网；能与固定干线网相连，多点接入；能与短波频谱检测系统实时交互信息[1]。由于短波通信组网的复杂性和特殊性要求，短波无线接入网成为了人们关注的重点。

无线接入网指用无线传播手段实现接入功能的网络[2]，其具体表现为用无线传输设备部分或完全地取代传统接入网中的馈线、配线和引入线。使用短波通信链路实现接入功能则是短波无线接入网的基本要求之一，由固定的接入基站、机动用户、探测系统及网络管理系统组成，各接入基站之间通过有线网络互联，各机动用户与接入基站通过短波链路链接，其具有机固一体、自适应接入、可通率高等优势。

然而，现有短波无线接入网抗人为干扰能力仍然存在不足，需要进一步提高。为此文献[3-4]提出了将智能跳频技术应用于短波无线接入网从而提高其链路抗干扰能力的思路。智能跳频技术的一个突出优点是非对称频谱配置，即：以本地可用频谱为优先对端发送频谱，两端的本地可用频谱未必相同。

若使用智能跳频的短波无线接入网仍采用固定式频谱分配方法对子网（短波无线接入网内的一个基站及其服务的机动用户组成一跳频子网）的可用频谱进行分配，可能与频谱利用率、频谱和用户实时调整等相矛盾，需要一种动态、快速、高效的频谱分配方法来适应短波无线接入网使用智能跳频技术的新需求。

智能跳频短波无线接入网基本通信需求主要体现在网路效益、网络支撑用户数、瓶颈用户吞吐量、频谱利用率、各子网满意度以及频谱分配公平性等方面。在实际使用中由于保障任务的轻重缓急各不相同，在有限的频谱资源环境下，要对其划分优先级次序，按照优先级高低优先保障特殊、紧急、重大任务，同时要求一种或两种以上的需求达到最充分满足。因此，要结合网络需求实现智能跳频短波无线接入网频谱的动态实时分配。

动态频谱管理及分配和用户动态用频之间紧密相关，动态频谱分配重点是制定相应的政策和频谱指配策略，用户用频是在分配政策下，一定范围内科学地动态用频[5]。目前动态频谱分配的模型主要有图论着色模型、拍卖竞价模型、博弈论模型和干扰温度模型等，如：文献[6]分析了可用频谱不满足需求时的频谱分配过程，提出一种公平性效用分配算法，可最大化满足用户需求；文献[7]提出的算法考虑了频谱和用户的优先级，可满足用户需求并提高分配效率；文献[8]提出了一种基于Markov排队理论的频谱分配算法，可有效提高吞吐量；文献[9]提出了一种频谱聚合机制，聚合不连续的频段来满足用户需求，将频谱抽象成很小的频谱单元，优先选择需求大的用户分配频谱；文献[10]针对图论频谱分配模型下最优频谱分配策略搜索解困难、耗时长的问题，提出一种采用多策略离散人工蜂群的频谱分配算法，可有效提高其搜索速率。这些频谱分配方法虽然能够完成可用频谱的分配，但是其研究领域都是频谱可以方便复用的认知无线电，对于短波通信的频谱分配研究还较少。

本文根据使用智能跳频的短波无线接入网的特殊要求，与认知无线电中的动态频谱分配区别主要如下：

1）分配目标不同。本文的分配模型是为各智能跳频子网分配短波频段，支撑子网内部的智能跳频通信，只要分配到了频段，子网内的接入基站和机动用户就可以完成智能跳频交互，实时进行非对称跳频，进而实现通信；而认知无线电网络频谱分配模型是通过伺机接入临时空闲频谱，为次级用户分配空闲频谱，实现对空闲频谱的再利用，提高频谱利用率。

2）实际要求不同。本文要分配频谱的对象——各子网之间地位平等，一个子网一旦接入，就会保证其通信直到结束；而认知无线电系统分配频谱过程中，主用户和次级用户相比具有更高的优先级，主用户一旦使用此频谱，次级用户立刻就要退出。

3）应用环境不同。本文分配模型是建立在短波无线接入网网络构架上的，其具有完整的探测感知、评估判决、信令交互和数据储存库机制，可以保障分配模型的动态实时性；而认知无线电分配模型是在实时感知外部频谱使用情况，发现并利用闲置的授权频段（频谱空穴）进行业务传输，实现频谱资源的动态共享，可认知环境的次用户只是伺机占用主用户未使用的授权频段进行通信。

本文采用基于图着色理论的动态频谱分配模型，总结提出动态频谱分配策略和算法，实验结果表明，使用此算法的智能跳频短波无线接入网，可明显提高网络效益、子网满意度和频谱利用率，并降低互扰率。

1系统模型

依据已有短波无线接入网的网络模型[3]，本文提出智能跳频技术应用于短波无线接入网的网络拓扑结构如图1所示。机动用户和接入基站都使用智能跳频技术，机动用户可以选择最优频率的基站接入通信。

对于可看作一个整体子网的某一基站及其服务的若干机动用户的频谱分配即是对各子网的分配。假设智能跳频短波无线接入网中有N个子网，所有的可用频带数为M，不同子网的需求不同。对各子网的频谱分配即是：在满足各子网需求的前提下，动态的M段频谱对N个子网进行分配。假设分配过程中的信息交互时间足够短，其时延对系统的影响可忽略不计；频谱感知、频谱分配以及业务传输的整个过程为一个周期，在一个周期内，网络拓扑结构不发生变化。

本文的动态频谱分配采用图论着色模型，分别由需求矩阵、可用频谱矩阵、互扰约束矩阵、频谱分配矩阵和效益矩阵描述，其频谱动态分配思路可表述如下：

2频谱分配策略

针对智能跳频短波无线接入网的不同通信需求，总结出五种频谱分配策略，这些策略以不同的目标实现频谱分配，并且都能够有效支撑智能跳频在短波无线接入网中的应用。

2.1最大化网络效益策略

最大化网络效益策略是指：智能跳频短波无线接入网的可用频谱分配给各子网时，以整体的频谱效益最大化为目标，同时最大化满足各子网的频谱需求，综合运用图着色理论完成可用频谱的分配。其可以定义为如下优化问题：

2.2最大化瓶颈用户的频谱效益策略

瓶颈用户的频谱效益是短波无线接入网服务质量的体现之一，因此，总结出对于智能跳频短波无线接入网的最大化瓶颈用户的频谱效益策略：在频谱分配过程中充分考虑瓶颈用户的频谱效益，使得瓶颈用户的频谱效益不会太小，从而提高网络的服务质量。

为提高瓶颈用户的频谱效益，引入以最大化瓶颈用户的频谱效益为目标的最优分配准则MMB （Max-Min-Bandwidth）[14]，其可表述为如下优化问题：

2.3最大化网络支持用户数策略

短波无线接入网支持用户数是衡量其服务能力的重要体现，也是人们对其承载能力的要求之一。最大化网络支持用户数策略是指：在分配的频谱满足用户需求的前提下，以网络支持用户数最大化为目标，对可用频谱进行分配。令Num表示网络支持的子网数，则最大化网络支持子网数的优化问题可表示为：

其中式（7）是优化问题的约束条件，保证分配给子网n的频带所带来的效益和能满足子网的需求。

2.4最大化网络公平性策略

网络公平性体现了将频谱分配给子网的均衡程度，减小了用户未分配到频谱的概率，保证所有用户分配到的频谱效益相当[15]。最大化网络公平性策略是指：以分配公平性最大化为目标，对可用频谱进行分配。

2.5最大化频谱利用率策略

频谱利用率体现了所有子网使用的频谱带宽占可用频谱总带宽的比重[17]。比重越大表示频谱利用率越高，比重越小频谱利用率越低。最大化频谱利用率策略是指：在频谱分配过程中，以频谱利用率最大化为目标，对可用频谱进行分配。

频谱利用率可以表示为子网使用的频谱分配矩阵之和与可用频谱之和的比值，可表示为如下优化问题：

3频谱分配算法

在智能跳频短波无线接入网的频谱分配中，将子网组成的网络映射成一个无向图G。图G中的每一个节点代表一个子网；每一条边连接某两个节点，表示这两个节点所对应的子网不能同时使用同一频带。此外，每个节点使用不同频带所带来的效益集合B（n）；每个节点关联着一个可选颜色集，即可用频谱集L（n），不同的节点关联不同的可用频谱集；与某一节点通过边相连的节点数为互扰连接度数Rn。根据以上定义，下面描述两种不同目标和约束的频谱分配算法。

3.1最大化网络效益频谱分配算法

步骤1初始化网络及无向图G。

步骤2根据各节点的效益集B（n）、可用频谱集L（n）以及需求矩阵，计算各节点使用各频带所带来效益及对应的可用频谱集，搜索拥有最大效益的节点n（子网n），按照最大效益对各节点分配频带；若出现几个节点具有相同的最大效益，则已分配的效益小的节点具有更高的优先级。

步骤3若此节点n的最大效益满足其频谱需求，则对节点n分配相应的频带m，更新节点信息，删除该节点及与其相连接的边，并且其邻接节点从对应的频谱集中去除已分配的频带；否则删除该节点及与其相连接的边。

步骤4计算互扰约束矩阵C，搜索与节点n同时使用频带m时无互扰的节点，若此节点之间也无互扰，则把频带m继续分配给此节点，同时更新节点信息。

步骤5若所有节点的可用频谱集为空，则分配结束；若所有节点的可用频谱集不为空，则根据上一阶段的分配计算节点满意度，得出各节点频谱分配优先级Z。

步骤6依据优先级高低对拥有最高优先级的节点n1分配相应的频带m1，更新节点信息；若有多个子网拥有相同的优先级，随机选取一个节点进行分配。

步骤7计算互扰约束矩阵C，搜索与节点n1同时使用频带m1时不产生互扰的节点，若这些节点之间也不产生互扰，把频带m1继续分配给这些节点，同时更新节点信息；若所有节点的可用频谱集为空，分配结束；否则返回步骤6。

步骤8依据优先级高低对拥有最高优先级的节点n1分配相应的频带m1，更新节点信息；若有多个子网拥有相同的优先级，随机选取一个节点进行分配。

步骤9计算互扰约束矩阵C，搜索与节点n1同时使用频带m1时不产生互扰的节点，若这些节点之间也不产生互扰，把频带m1继续分配给这些节点，同时更新节点信息；若所有节点的可用频谱集为空，分配结束；否则返回步骤6。

算法综合考虑了频谱分配所带来的网络效益、子网满意度以及对相邻节点的影响，同时增加了频谱可以空间复用的特殊要求。若一个节点n分配频带m，由于与该节点相邻的Rn个节点也无法使用频带m，而其他n-Rn节点可以使用频带m，所以这次分配对整个系统总效益的贡献值为bn，m/（Rn+1）。算法通过多轮运算逐步实现网络效益和子网满意度最大化为目标的频谱分配。

3.2最大化网络支持用户数频谱分配算法

步骤1初始化网络及无向图G。

步骤2根据各节点的效益集B（n）、可用频谱集L（n）以及需求矩阵计算各节点使用各频带所带来的效益及对应的可用频谱集。

步骤3按照需求矩阵由小到大的顺序，选择分配的节点n，计算节点n的可用频谱的效益和是否满足需求；若不满足，则删除图G的该节点及与其相连接的边，返回步骤2。

步骤4对节点n按照L（n）值从大到小依次分配频带{m，m+1，…}，直到节点n的效益需求得到满足，若此节点使用多个频带有相同的最大效益，则随机选取一个频带分配。

步骤5节点n频谱分配完成，退出分配，更新节点信息，删除该节点以及与其相连接的边，并且其邻接节点从对应的频谱集中去除已分配的频带。

步骤6计算互扰约束矩阵C，搜索与节点n同时使用频带{m，m+1，…}时无互扰的节点，若此节点之间也无互扰，把频带m继续分配给此节点，同时计算其带来的频谱效益是否满足需求，若满足，则更新节点信息；若不满足，则返回步骤2；直到所有节点的可用频谱集L（n）为空，分配结束。

算法在满足子网需求的基础上以最大化网络支持用户数为目标进行频谱选择及分配，同时考虑了频谱空间复用的情况。

4仿真分析

应用所提两个不同目标的动态频谱分配算法对智能跳频短波无线接入网各子网的可用频谱进行分配仿真，并且与传统的固定式频谱分配方法[18]及不考虑频谱空间复用情况下的频谱分配进行对比。仿真参数如表1所示。

模型设计过程中充分考虑短波通信频谱资源紧缺、面临使用用户多的特征，设置子网数多于频带数，当不考虑频谱空间复用时，就有用户不能满足通信需求，频谱空间复用时，则有望都能满足；结合短波通信覆盖范围广的特征设置网络覆盖范围为2000km×2000km，子网覆盖半径至少达到400km、至多达到1000km是合适的；精确起见，频谱恶化率 p在[0，1]区间每隔0.05取值一次；效益矩阵B设置为一个子网使用一段频谱得到的效益是1个单位到10个单位不等。

本文只考虑电磁频谱环境变化带来的可用频谱恶化的情形，并且假设短波无线接入网各子网的可用频点全部为智能跳频频率表的频点。频谱恶化会导致可用频谱的频点数减少。假设未恶化的频点误码率为10-4，发生恶化的频点误码率为0.98。电磁频谱恶化率p（0≤p≤1）定义为：误码率由10-4变为0.98的频点数与频率表总频点数的比值。

为表述方便，将仿真对比的算法及使用环境作如下说明，如表2所示。

4.1频谱分配仿真

对预分配的频谱依次编号1～20，如表3所示。表3中一个数据是指此子网只分配到了1个频带，两个数据是指分配到了2个频带，数字大小是指频带的编号。

由表3可知，当电磁频谱环境较好，其恶化率p=0，子网数n=10时，固定式频谱分配方法可以满足各子网频谱需求；当电磁频谱恶化率p=0.5时，固定式谱分配方法无法满足各子网的需求；而频谱可以空间复用时，最大化网络效益分配算法及最大化网络支持用户数分配算法可使各子网都分配到自身可用的频带，而且分配的频带数显然更多；表3最后一行是不考虑频谱空间复用的分配结果，各子网也都分配到自身可用的频带，但其频带数显然少于频谱可空间复用的情形。

4.2网络效益仿真分析

网络效益的仿真，如图2所示。由图2可知：当电磁频谱发生恶化时，使用智能跳频明显高于采用定频通信所带来的网络效益；使用最大化网络效益算法和最大化支持用户数算法所带来的网络效益明显高于不考虑空间复用分配算法及固定式频谱分配方法；频谱可以空间复用显著高于不可空间复用所带来的网络效益。其中图2（a）表示根据最大化网络效益分配算法，随着仿真次数的增加，网络效益迅速达到最大，而固定式频谱分配方法所带来的网络效益基本不变。

4.3子网满意度仿真分析

采用最大化网络效益频谱分配算法和最大化支持用户数频谱分配算法对智能跳频短波无线接入网的可用频谱进行分配过程中，各子网的平均满意度如图3所示。由图3可知：最大化网络效益算法和最大化支持用户数算法都可以保证分配到频谱的子网的满意度大于1。

4.4网络支持用户数仿真分析

最大化支持用户数频谱分配算法随着电磁频谱恶化率变化所支持的最大子网数量如图4所示，其中：n2、n3分别表示最大化网络支持用户数算法和使用固定式频谱分配方法的子网数量。由图4可知：相同的子网数量条件下，最大化网络支持用户数算法所能支撑的子网数量比固定式频谱分配方法所能支撑的子网数量更多；同时，随着电磁频谱恶化率的增大，两种算法所支撑的子网数量随之减少。

4.5频谱利用率仿真分析

频谱利用率的仿真，如图5所示。由图5可知：当电磁频谱发生恶化时，智能跳频明显高于定频通信所带来的频谱利用率；最大化网络效益分配算法所带来的频谱利用率高于其他算法；固定式频谱分配方法所带来的频谱利用率最低；可以空间复用相对于不可复用所带来的频谱利用率更高。其中图5（a）显示根据最大化网络效益分配算法，随着仿真次数的增加，频谱利用率迅速达到最大值，而固定式频谱分配方法所带来的频谱利用率基本不变。

4.6互扰率仿真分析

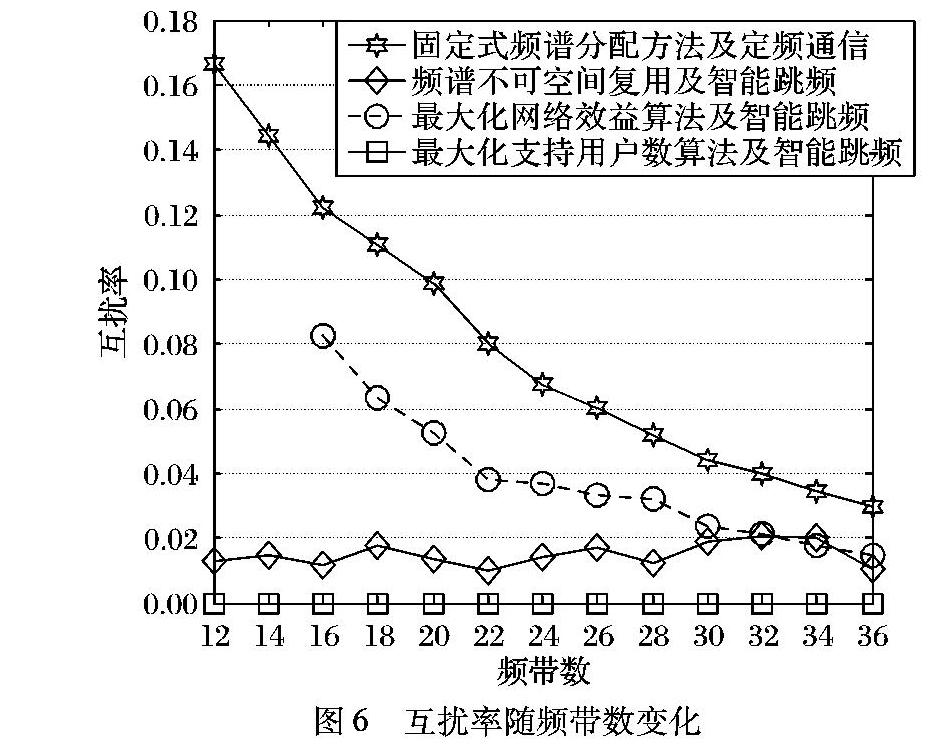
若智能跳频短波无线接入网未使用本文所提动态频谱分配算法分配频谱，智能跳频的非对称频谱配置会在所有可用频谱上进行，各子网之间就会产生严重的互扰。互扰率是指：各子网内的基站与机动用户通信过程中子网相互之间产生互扰的概率。子网1与其他子网的互扰率仿真，如图6所示。由图6可知：本文所提动态频谱分配算法所带来的互扰率明显小于固定式频谱分配；并且子网1与其他子网的互扰率平均值随着频带数的增加逐渐降低，且都维持在较低水平。

5结语

本文针对现有短波无线接入网采用固定式频谱分配方法，难以适应频谱动态变化及使用智能跳频技术新要求的问题，分析智能跳频短波无线接入网的通信需求，结合图着色理论模型，总结提出不同目标的频谱分配策略和主要的频谱分配算法。该算法能够快速、高效、准确地完成频谱动态分配，有效支撑智能跳频技术在短波无线接入网中的应用，提高短波无线接入网抗动态干扰能力。仿真结果表明，在相同的互扰约束下，与使用固定式频谱分配方法的定频通信相比，其可带来网络效益、子网满意度、网络公平性、网络支持用户数和频谱利用率等方面的显著提升，同时互扰率有效降低。

参考文献：

[1]姚富强.通信抗干扰工程与实践[M].2版.北京：电子工业出版社，2012：312-313. （YAO F Q. Communication Anti-jamming Engineering and Practice [M]. 2nd ed. Beijing： Publishing House of Electronics Industry， 2012： 312-313.）

[2]张冬辰，周吉.军事通信——信息化战争的神经系统[M].2版.北京：国防工业出版社，2008：472-473. （ZHANG D C， ZHOU J. Military Communication [M]. 2nd ed. Beijing： National Defence Industry Press， 2008： 472-473.）

[3]段瑞杰，姚富强，李永贵，等.基于智能跳频的短波无线接入网抗干扰性能分析[J].通信技术，2016，49（2）：153-158. （DUAN R J， YAO F Q， LI Y G， et al. Anti-jamming performance of HF radio access network based on intelligent frequency hopping [J]. Communications Technology， 2016， 49（2）： 153-158.）

[4]段瑞杰，李永贵，惠显杨.短波无线接入网抗干扰需求分析[J].通信技术，2015，48（7）：818-824. （DUAN R J， LI Y G， HUI X Y. The need analysis of anti-jamming for HF radio access network [J]. Communications Technology， 2015， 48（7）： 818-824.）

[5]姚富强，张建照，柳永祥，等.动态频谱管理的发展现状及应对策略分析[J].电波科学学报，2013，28（4）：192-201. （YAO F Q， ZHANG J Z， LIU Y X， et al. Review of the development of dynamic spectrum management and the resolving strategies analysis [J]. Chinese Journal of Radio Science， 2013， 28（4）： 192-201.）

[6]PAUL A， MAITRA M， MANDAL S， et al. A metaheuristic based fair dynamic spectrum allocation policy [C]// ANTS 2011： Proceedings of the 2011 Fifth IEEE International Conference on Advanced Networks and Telecommunication Systems. Washington， DC： IEEE Communications Society， 2011： 1-6.

[7]ZHANG X-C， HE S-B， SUN J. A game algorithm of dynamic spectrum allocation based on spectrum difference [C]// WOCC 2010： Proceedings of the 2010 19th Annual Wireless and Optical Communications Conference. Washington， DC： IEEE Communications Society， 2010： 1-4.

[8]WANG B， JI Z， LIU K J R， et al. Primary-prioritized Markov approach for dynamic spectrum allocation [J]. IEEE Transactions on Wireless Communications， 2009， 8（4）： 1854-1865.

[9]张华晶，徐少毅，乔晓瑜.认知无线电网络中基于用户需求和频谱聚合的动态频谱分配[J].电信科学，2010，26（12）：63-67.） （ZHANG H J， XU S Y， QI X Y. Dynamic spectrum allocation algorithm based on user demands and spectrum aggregation in cognitive radio networks [J]. Telecommunication Science， 2010， 26（12）： 63-67.

[10]朱冰莲，朱方方，段青言，等.采用多策略离散人工蜂群的改进频谱分配算法[J].西安交通大学学报，2016，50（2）：20-25. （ZHU B L， ZHU F F， DUAN Q Y， et al. An improved spectrum allocation algorithm using multi-strategy discrete artificial bee colony technology [J]. Journal of Xian Jiaotong University， 2016， 50（2）： 20-25.）

[11]李小强，周琦，芮茂海，等.频谱异构认知无线电中基于吞吐量降的空时频谱机会感知[J].电子与信息学报，2014，36（11）：2762-2768. （LI X Q， ZHOU Q， RUI M H， et al. Spatial-temporal opportunity sensing based on throughput loss in spectrum-heterogeneous cognitive radio [J]. Journal of Electronics and Information Technology， 2014， 36（11）： 2762-2768.）

[12]蒋梦雄.基于图论的认知无线电频谱分配研究[D].哈尔滨：哈尔滨工业大学，2010：2-4. （JIANG M X. Spectrum allocation based on graph theory in cognitive radio network [D]. Harbin： Harbin Institute of Technology， 2010： 2-4.）

[13]杜文峰，刘亚涛，明仲，等.基于干扰消减的认知无线电频谱分配算法[J].通信学报，2012，33（5）：106-115. （DU W F， LIU Y T， MING Z， et al. Interference elimination based spectrum allocation algorithm for cognitive radio [J]. Journal on Communications， 2012， 33（5）： 106-115.）

[14]席志红，晋野，李娅.认知无线电的频谱分配算法[J].应用科技，2010，37（2）：10-13. （XI Z H， JIN Y， LI Y. Spectrum allocation algorithm in cognitive radio [J]. Applied Science and Technology， 2010， 37（2）： 10-13.）

[15]胡庆，常迪，海力群.认知无线电中基于频谱聚合的需求改进型频谱分配算法[J].重庆邮电大学学报（自然科学版），2014，26（1）：8-12. （HU Q， CHANG D， HAI L Q. Spectrum allocation algorithm based on spectrum aggregation and user demands in cognitive radio [J]. Journal of Chongqing University of Posts and Telecommunications （Natural Science Edition）. 2014， 26（1）： 8-12.）

[16]瞿越，鲜永菊，徐昌彪.基于用户需求的图着色论频谱分配算法[J].计算机应用，2011，31（3）：602-605. （QU Y， XIAN Y J， XU C B. Spectrum allocation algorithm of graph coloring theory based on user requirement [J]. Journal of Computer Applications， 2011， 31（3）： 602-605.）

[17]YANG L， XIE X， ZHANG Y. A historical-information-based algorithm in dynamic spectrum allocation [C]// ICCSN 2009： Proceedings of the 2009 International Conference on Communication Software and Networks. Washington， DC： IEEE Computer Society， 2009： 731-736.

[18]刘勤，李红霞，李钊，等.基于认知的LTE系统动态频谱分配[J].电子与信息学报，2015，37（1）：175-182. （LIU Q， LI H X， LI Z， et al. Dynamic spectrum allocation for LTE system by exploiting cognitive capability [J]. Journal of Electronics and Information Technology， 2015， 37（1）： 175-182.）