基于三层集成多标记学习的蛋白质多亚细胞定位预测
乔善平 闫宝强
摘要:针对多标记学习和集成学习在解决蛋白质多亚细胞定位预测问题上应用还不成熟的状况,研究基于集成多标记学习的蛋白质多亚细胞定位预测方法。首先,从多标记学习和集成学习相结合的角度提出了一种三层的集成多标记学习系统框架结构,该框架将学习算法和分类器进行了层次性分类,并把二分类学习、多分类学习、多标记学习和集成学习进行有效整合,形成一个通用型的三层集成多标记学习模型;其次,基于面向对象技术和统一建模语言(UML)对系统模型进行了设计,使系统具备良好的可扩展性,通过扩展手段增强系统的功能和提高系统的性能;最后,使用Java编程技术对模型进行扩展,实现了一个学习系统软件,并成功应用于蛋白质多亚细胞定位预测问题上。通过在革兰氏阳性细菌数据集上进行测试,验证了系统功能的可操作性和较好的预测性能,该系统可以作为解决蛋白质多亚细胞定位预测问题的一个有效工具。
关键词:蛋白质多亚细胞定位预测;多标记学习;集成学习;面向对象技术;Java
中图分类号:TP391
文献标志码:A
0引言
蛋白质亚细胞定位对于确定蛋白质功能、阐明蛋白质相互作用机制和新药物开发等都具有重要意义。蛋白质亚细胞定位的传统方法是通过生物化学实验进行测定,如荧光检测法[1]和谱分析法[2]等。虽然实验方法准确度高,但费时耗力、代价昂贵,实验中还会出现偶然因素的干扰,致使测定工作冗长且不稳定。DBMLoc数据库[3]的统计结果表明,具有多个亚细胞位置的蛋白质数量不断增长且功能特殊,如何对这类蛋白质进行亚细胞定位是一个非常值得研究的问题。然而,相对于单亚细胞定位而言,不论是采用实验方法,还是基于计算技术的预测方法,蛋白质多亚细胞定位问题都具有更大的挑战性[4]。在过去的20多年中,针对蛋白质的单亚细胞定位预测,利用统计学习和监督学习已取得了较大的成功[5-6]。但对于蛋白质的多亚细胞定位预测,自2005年Chou等[7]和Gardy等[8]分别开始研究以来,目前还远未达到人们所期待的水平,需要进行更深入的探索[9]。
从机器学习的角度来看,蛋白质多亚细胞定位预测问题属于多标记学习的范畴。在多标记学习框架中,每个对象由一个示例描述,该示例具有多个而不再是唯一的类别标记,学习的目标是将所有合适的类别标记(即标记集)赋予待测示例。近年来,虽然多标记学习技术得到了较快的发展[10],但在解决蛋白质多亚细胞定位预测问题上的应用却不太成熟,特别是能够将集成学习与多标记学习相结合的研究还很少,尚有很多内容需要研究:第一,针对蛋白质数据的海量、关联性和不完整等复杂特征,需要设计更加适合于解决蛋白质多亚细胞定位问题的学习算法,或者引入更多现有的多标记学习方法,以扩展多标记学习技术在该领域的应用;第二,需要将多标记学习和集成学习更好地结合来构建学习系统,以充分发挥集成学习的优势;第三,需要设计扩展性好、易于使用且具有一定通用性的学习系统平台,为相关研究人员提供良好的技术和服务支持。
基于上述思路,本文提出了一种三层集成多标记学习框架,通过将学习算法和分类器进行层次性分类,并把多种学习模型合理地综合在一起,形成了一种通用型的集成多标记学习模型;在该模型基础上,使用面向对象技术并结合统一建模语言(Unified Modeling Language, UML)设计了一个可扩展的多层集成多标记学习系统;最后构建了一套基于Java技术的集成多标记学习软件,为基于机器学习的蛋白质多亚细胞定位预测提供了一条有效途径。
1学习系统的框架结构
为了能更清晰地对系统进行描述和便于理解,这里将“学习算法”和“分类器”这两个概念进行了必要的区分:学习算法是指解决某个一般性学习问题的一种方法,如K最近邻(K Nearest Neighbor, KNN)和支持向量机(Support Vector Machine, SVM)等;而分类器则是一个学习算法针对某个特定的分类问题(如癌症分类、蛋白质亚细胞定位等)在给定的基准训练数据集(如基因表达数据集、蛋白质序列数据集等)上的一个具体实现,是解决某个一般性分类问题的实例,它通常是由某个学习算法通过优化算法结构或优化其中的某些参数而产生出来的。
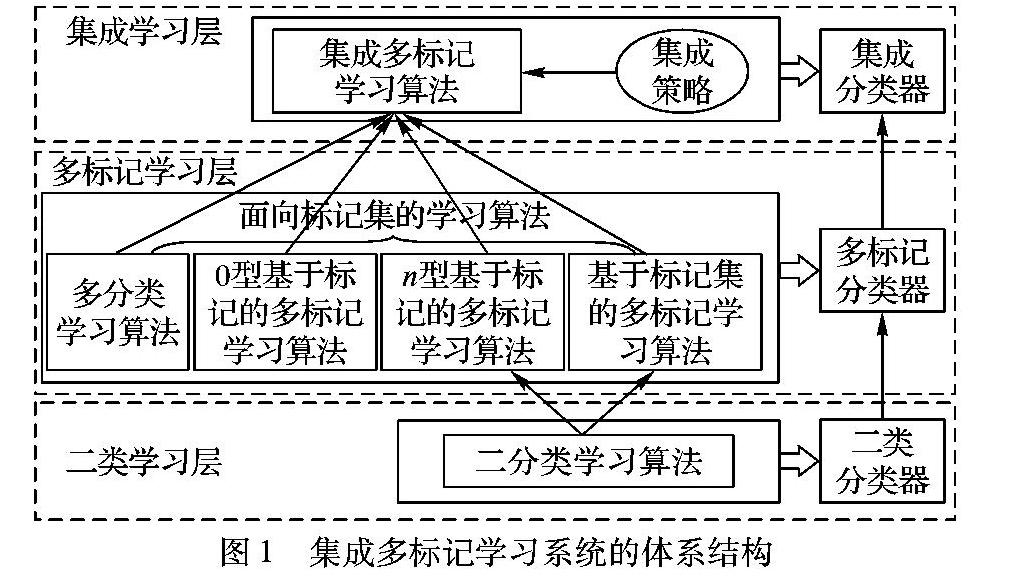
在集成多标记学习框架下,本文把学习算法分为二分类学习算法、面向标记集的学习算法和集成多标记学习算法三大类;相应地,分类器分为二分类器、多标记分类器和集成分类器三大类。图1所示是本文所建立的集成多标记学习系统的框架体系结构以及各部分之间的依赖关系。该结构共包括三层:二分类学习层、多标记学习层和集成学习层。二分类学习层针对二分类学习算法和二分类器,多标记学习层针对面向标记集的学习算法和多标记分类器,集成学习层针对集成多标记学习算法、集成策略和集成分类器。值得注意的是,属于同一层的分类器可以由位于同层但不同种类的学习算法产生出来,例如:对于一个二类分类器,既可以使用KNN算法生成,也可以通过SVM算法获得。
1.1二分类学习层
二分类学习层是三层中最为简单的一层,任何能够解决二分类问题的算法(如KNN和SVM等)都可以归到这一层。一个二分类算法用来在给定的二类训练数据集上产生一个二分类器。一个二分类器被成功构建出来后便可用于二分类问题的求解。对于给定的待测示例,一个二分类器能够返回两个可能标记(一般使用正例和负例表示)中的一个。为了具有更一般的表达形式,假设一个二分类器总是可以为待测示例计算出一个位于区间[-1,+1]的实数,该实数用来度量所预测出的标记(若为正数则表示正例标记,否则为负例标记)隶属于待测示例的程度,在后期的处理中可再将这个实数值转换为相应的类别标记。
二分类学习层中的二分类算法通常会由其上层即多标记学习层中的某些学习算法在训练阶段所利用,这类算法需要使用若干二分类算法来辅助完成它们自己的学习任务。不同的二分类算法可以同时被多标记学习层中的某个算法所雇用,即可以是异构的。然而,一般来说,由于从不同类型的二分类算法产生出来的二分类器所采用的计算准则可能并不一样,造成它们返回的度量值有着不同的含义,尽管它们的取值区间相同。例如:对于分别从KNN和SVM产生出来的两个二分类器,即使它们返回的度量值都是0.5,但正例标记隶属于待测示例的程度可能不同,这与它们所产生的实际度量区间有较大的关系,这是多标记学习层中的某些算法在进行集成时所面临的一个问题。因此,在二分类器异构情况下,一个重要问题是建立一种统一的度量标准,使得这些度量值具有较好的可比性,本文尚未对这种度量标准进行深入的研究。
1.2多标记学习层
多标记学习层用来在面向标记集的学习算法基础上生成多标记分类器。面向标记集的学习算法划分为四种类型:多分类学习算法、0型基于标记的多标记学习算法、n型基于标记的多标记学习算法和基于标记集的多标记学习算法。之所以把这些算法归到这一层,是因为它们都可以直接或经过某些修改后用来解决多标记学习问题,并且都可以为待测示例预测出一个标记集。因此,它们统称为“面向标记集的学习算法”。类似地,本层为其上层即集成学习层提供支持。
1.2.1多分类学习算法
多分类学习算法是用来对含有两个以上类别标记的分类问题进行学习的一种算法,如KNN、神经网络、决策树等都可以归为这一类。经过一定的变换,一个多标记学习问题可以转换为一个多分类问题,由此就可以使用这样的多分类学习算法来解决多标记学习问题,所以在这种意义上本文将多分类学习算法作为一种面向标记集的学习算法看待。
1.2.2基于标记的多标记学习算法
基于标记的多标记学习算法分别考虑单个标记来执行学习任务,然而为了提高学习系统的泛化能力,标记之间的关联性是需要给予考虑的一个重要方面。形式上,令X=Rd表示d维示例空间,L={l1,l2,…,lq}表示含有q个标记的标记空间,则基于标记的多标记学习算法的学习任务可以通过两个实值函数来辅助完成。第一个函数是f(x,lj),用来表示示例x拥有标记lj的可信度;第二个函数是一个阈值函数t(x),用来度量第一个函数的返回值,由此来确定与示例x相关联的标记集。由此,预测待测示例x的标记集可以用函数h(x)={lj|f(x,lj)>t(x),x∈X,lj∈L,1≤j≤q}实现。
依据学习算法是否需要利用二分类学习层中的二分类学习算法来辅助完成其学习任务,可以进一步把这类算法分为两个子类型,即0型基于标记的多标记学习算法和n型基于标记的多标记学习算法。0型算法可以独立地执行学习任务而不需要利用二分类学习层中的任何二分类算法。相反地,n型算法在学习过程中则需要使用若干二分类学习算法来支持学习任务的执行,最后再按照某种策略将每个二分类器的分类结果进行综合来产生一个标记集作为最终的分类结果。至于需要多少个二分类器(即n的取值)的支持,这取决于所设计的策略。例如,在最为简单的一对其余策略中,如果数据集中含有q个标记,则需要q个二分类器;而在一对一策略中,需要的分类器数量则是q(q-1)/2。
1.2.3基于标记集的多标记学习算法
基于标记集的多标记学习算法是从训练数据集中学得一个函数,使用该函数可以为待测示例直接预测一个与之相关联的标记集。由于标记集的数目会随着标记数目的增长而呈指数增长,所以问题的复杂度也会快速增长。一般情况下,限于样本搜集的繁琐性和数据整理的困难性,在所构建的训练数据集中,标记集的数量往往并不是很多,通常只包括所有可能标记集的一部分,这实际上可以在一定程度上降低问题的复杂度。然而,这种学习方式中一个明显的缺点就是对于那些未出现在训练集中的标记集很难预测出来。
多分类算法和0型基于标记的多标记学习算法都可以独立地执行学习任务而不需要任何二分类算法的支持。二者的区别在于前者可以直接产生一个标记集作为预测结果,而后者则需要先在每个标记上进行预测,最后再组合成一个标记集,其优势在于可以产生包含在训练集以外的标记集。相反地,对于n型基于标记的多标记学习算法和基于标记集的多标记学习算法,它们都必须利用若干二分类算法来辅助完成学习任务。二者的区别在于前者是在单个标记上进行学习,而后者则是在标记集上进行学习。
1.3集成学习层
集成学习层通过解决两个紧密相关的问题来产生最终的集成分类器:一是如何控制来自下层(包括多标记学习层和二分类学习层)的各学习算法的执行过程以产生个体分类器;二是如何利用个体分类器所提供的结果来确定在集成中所包含的标记信息,为此需要进行集成策略和集成算法的设计。
1.3.1集成策略
当所有的个体分类器完成学习任务后,还需要利用集成策略来决定集成结果中需包含的标记信息,以及如何生成最终的集成分类器。一个集成策略的主要任务是从所有的个体分类器中选出一组同时具有一定准确性和多样性的个体分类器,根据每个分类器的性能和类型为它们分别设定一个合适的权值,然后为每个待测示例产生一个最终的标记集。最常见的集成方式是在个体分类器的输出结果上进行,集成策略决定如何利用个体分类器中包含的结果信息来构造标记集,如采用投票、集合运算、计算概率等策略。另外,集成也可以在使用不同特征的分类器上进行。对于多义性对象而言,将不同的特征向量与不同的算法相关联,以反映不同的语义表示,这样得到的分类结果往往比一个算法使用所有的特征融合所产生的分类结果要好。然而,自动特征选择,特别是在多标记学习中依然具有很大的挑战性。
1.3.2集成算法
一个集成算法的主要任务是引导所有来自二分类学习层和多标记学习层的学习算法在给定的数据集上完成训练和测试过程,以便生成个体分类器并度量它们的性能,由此建立一个集成模型供集成策略使用。要完成集成多标记学习的过程并生成一个最终的集成分类器,需要以下基本步骤:
1)提交:选择特征表示法、学习算法、数据集、度量指标、训练阶段的验证方法及其参数、测试阶段的验证方法及其参数,进行提交以生成个体分类器和集成模型。
2)集成:选择需要集成的个体分类器、使用的集成策略、集成方式,进行集成以生成集成分类器。
3)提升:通过对集成分类器执行优化和过滤等操作进一步提升集成分类器的性能。
在上面三个步骤中,前两步是必需的,这两步执行完毕后即可生成一个集成分类器。第三步是为了进一步提升集成分类器的性能而提供的基于智能计算技术的包括优化和过滤等手段在内的一个可选步骤。在这个步骤中,目前尚存在很多待解决的关键问题,如优化算法的选择和执行效率、对标记进行过滤的标准设定等。
另外,为了使学习过程可视化和便于操作,集成算法的执行过程应与用户界面相结合,将学习过程直观地在界面上实时展示出来。整个学习过程有时需要经过若干次的迭代,通过设定不同的参数和多次优化操作,一个性能良好的集成多标记学习分类器才能被成功产生出来。
2学习系统的设计与实现
可扩展性对一个学习系统来说非常重要,其原因有:首先,现实中存在很多的特征表示法、学习算法和集成策略,理论上它们都可以被引入到系统中,但在一个系统中却很难把它们都实现出来。更为重要的是,很多新的特征提取方法、算法和集成策略也会不断地被提出来,这些都关系到系统的扩展。所以,如果系统具有良好的可扩展性,就使得引入这些算法和策略成为可能。再者,可扩展性同时也带来了灵活性,使得用户可以按照自己的特定需求对系统进行定制。
2.1学习系统的类体系结构设计
本文通过对特征、算法及其数据模型、集成策略等实体进行分析和设计,使用面向对象技术和UML建模工具对系统进行了详细设计,为系统扩展建立了良好的接口。形成了以Algorithm和Classifier两个抽象类为扩展学习算法和分类器的基础,以LabelApplicable和LabelsetApplicable两个接口为定义基于标记和基于标记集学习算法的标志,以EnsembleAlgorithm类控制从数据提交到实现集成、优化和过滤的整个过程。以此为基础,在实现新的学习算法、集成策略和特征表示法方面,建立了以下几个扩展点:
1)BinaryClassAlgorithm:用于扩展二分类学习算法。
2)MultiClassAlgorithm:用于扩展多分类学习算法。
3)LabelBasedAlgorithm0:用于扩展0型基于标记的多标记学习算法。
4)LabelBasedAlgorithmN:用于扩展n型基于标记的多标记学习算法。
5)LabelsetBasedAlgorithm:用于扩展基于标记集的多标记学习算法。
6)Model:用于扩展与学习算法相对应的数据模型。
7)EnsembleStrategy:用于扩展新的集成策略。
8)Feature:用于扩展新的特征提取和表示方法。
在上述这些类和接口的基础上,构建一个集成多标记学习系统的主要任务就是从上述扩展点进行扩展,为系统添加新的学习算法及其数据模型、集成策略和特征提取方法等相关内容,并结合系统配置文件灵活地将这些扩展部分添加到系统中,从而增强系统的功能和提高系统的性能。因此,本文中所设计的集成多标记学习系统具有良好的可扩展性和开放性。从广义上说,它是一个通用型的学习系统,不仅可以用于蛋白质亚细胞定位问题的研究,还能够适应于更多分类问题的求解。
2.2学习系统的扩展实现
针对蛋白质多亚细胞定位预测问题,本文使用支持面向对象技术的Java语言,在特征表示、学习算法和集成策略等方面进行了扩展和实现。
1) 特征表示:实现了氨基酸组成(Amino Acid Composition, AAC)[11]、伪氨基酸组成(Pseudo Amino Acid Composition, PseAAC)[12]、两性伪氨基酸组成(Amphiphilic Pseudo Amino Acid Composition, AmPseAAC)[13]、类模式频率(Class Pattern Frequency, CPF)和蛋白质相似性度量(Protein Similarity Measure, PSM)[14]等蛋白质特征提取和表示方法。
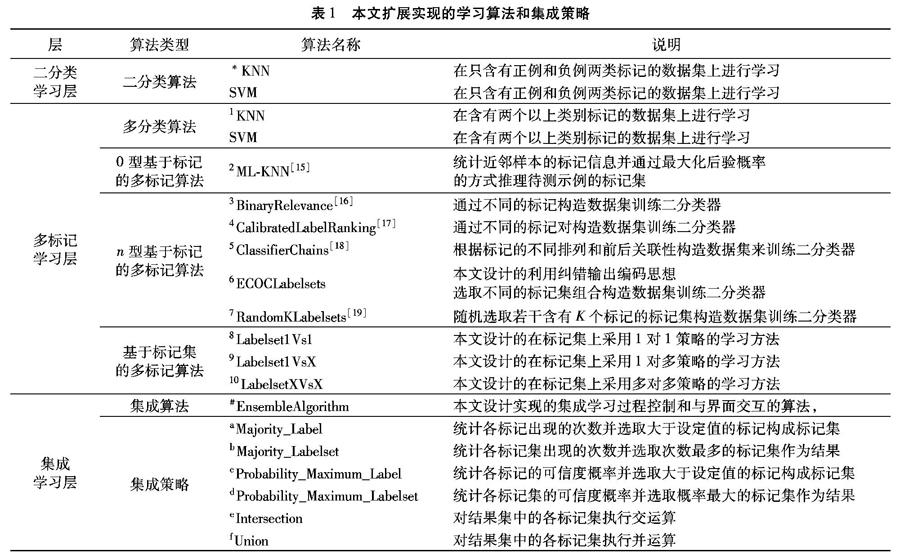
2) 学习算法和集成策略:本文实现的学习算法和集成策略如表1所示。
3学习系统的应用与结果分析
3.1数据集
本文采用由Shen等[20]于2009年构建的革兰氏阳性细菌蛋白质数据集,该数据集共包含519条蛋白质序列数据,并且任意两条蛋白质之间的序列同源性都不超过25%,有效避免了序列同源性对预测结果的影响。数据集中共涉及到4种不同的亚细胞位置和7种不同的亚细胞位置集合。在这519条蛋白质序列中,长度最长的含有2334个氨基酸,最短的含有55个氨基酸,平均氨基酸个数约为424。
在PseAAC和AmPseAAC中都有两个待优化的参数w和λ,本文使用网格法对两种特征提取方法分别在选择的训练数据集上进行搜索以寻找最优值。设定w的取值区间为[0,1],步长为0.01;λ的取值区间为[1,10],步长为1。通过搜索,对于PseAAC,得到了两个参数的取值分别为w=0.01和λ=7,而AmPseAAC对应的两个参数的取值分别为w=0.2和λ=6。由此,使用这两种特征表示法时每条蛋白质序列分别表示为长度为27和32的两个实向量。
3.3学习过程
本文以表1中标注为*的KNN作为二分类学习层中的学习算法,以标注为1~10的10种算法作为多标记学习层的学习算法,使用标注为#的集成算法和标注为a~f的6种集成策略进行实验。在训练阶段,对于KNN和ML-KNN算法设定K的搜索区间为[1,50],对于ClassifierChians和RandomKLabelset算法则采用随机的方式,然后使用10次交叉验证来训练各个个体分类器;在测试阶段,采用Jackknife测试对个体分类器的性能进行度量,并生成一个包含20个个体分类器信息的集成模型。最后,使用粒子群优化(Particle Swarm Optimization, PSO)算法[21]优化算法在20个分类器上进行选择,产生出一组分类器组合,通过在这组分类器上分别应用6种不同的集成策略后,得到最终的集成分类器。
3.4性能度量指标
对于一个样本空间大小为m、标记空间大小为q的测试数据集,令Yi和Y*i分别表示测试集中第i个样本的真实标记集和预测标记集,则有式(10)所示的5个常用的度量指标:
在上述指标中,Absolute-True是最为严格的一个指标,在多标记学习框架下,它用来度量被完全正确预测的样本数量占测试集样本总数量的比例,其值越大越好。在训练阶段即采用该指标作为目标值进行参数的优化。Hamming-Loss(又称为Absolute-False)则是用来度量被错误预测的标记情况,其值越小越好。Recall、Precision和Accuracy分别表示正确预测出的标记占真实标记、预测标记和整体标记(包括真实标记和预测标记)的比例,它们的值都是越大越好。
3.5结果分析
训练后生成的20个个体分类器的性能指标如表3所示,其中指标1~5分别表示Absolute-True、Hamming_Loss、Recall、Precision和Accuracy;A1~A10分别表示10种学习算法;F1和F2分别表示PseAAC和AmPseAAC两种特征表示法;下划线表示使用PSO算法选择出的分类器组合(后续表格中采用相同的表示方法,不再重复说明)。
从表3可以看出,在20个个体分类器中,Absolute-True的最大值为0.7611,最小值为0.6840,并可以计算出平均值为0.7330。得到的分类器组合中共包含了3个个体分类器,分别是ML-KNN+PseAAC、ML-KNN+AmPseAAC和Labelset1VSX+AmPseAAC,它们对应的Absolute-True的值分别为0.7148、0.7572和0.7476。直观地看,这组分类器具有合适的规模、较高的准确性和较好的多样性,为进行集成操作提供了有利条件。通过应用不同的集成策略,最后得到使用Probability_Maximum_Label集成策略的结果最好,如表4所示。
从表3和表4可以看出,集成分类器的Absolute-True指标值为0.7765,高于3个分类器中的任何一个,而Hamming-Loss指标值为0.1113,低于3个分类器中的任何一个,这些结果从不同方面都验证了集成方法的有效性。
为了进一步验证本文所设计方法的性能,将有关结果与文献[22]进行了比较。文献[22]使用了N端信号肽、PseAAC、氨基酸指数分布(Amino Acid Index Distribution,AAID)、理化特性模型和立体化学属性共5种特征表示方法,并将它们以不同的方式进行融合,使用ML-KNN算法,在与本文所使用的相同训练数据集上完成了分类器的训练,得到了一个最好的分类器,其性能指标也列于表4中。该分类器的Absolute-True指标值和Hamming-Loss指标值分别为0.6673和0.1440。显然,本文的结果在这两个指标上都更好,其中Absolute-True指标值高出近11个百分点,而Hamming-Loss指标值则低3个多百分点。
为了验证多特征集成方法与多特征融合方法的优劣,首先将PseAAC和AmPseAAC两种特征进行了融合,产生出长度为27+32=57的特征向量(用F1+F2表示),然后分别对10种学习算法在相同的数据集上进行训练,得到10个个体分类器,它们的性能指标如表5所示。
接下来,对每种学习算法在PseAAC和AmPseAAC特征上产生的两个分类器进行集成(用F1^F2表示特征),同样得到10个个体分类器,它们的性能指标如表6所示。
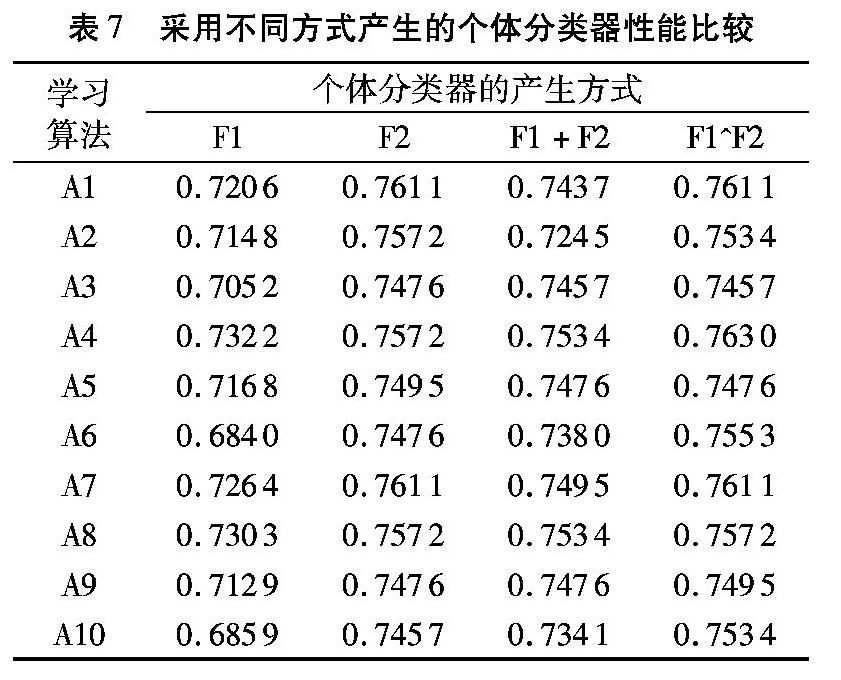
最后,以Absolute-True为主要度量指标,将10种学习算法分别在特征F1、F2、F1+F2、F1^F2上所产生的个体分类器进行了性能比较,结果如表7所示。
分析表7中的数据可以看出,采用特征集成所产生的分类器性能总是不次于采用特征融合产生的分类器,这说明在多个特征上进行集成的方法要好于特征融合所产生的效果。分析原因,初步认为在集成过程中个体分类器之间具有一定的互补性,提高了集成分类器的性能。
4结语
本文结合多标记学习和集成学习两方面的内容设计了一种多层的集成多标记学习系统,并在蛋白质多亚细胞定位预测问题上进行了应用。测试表明,系统能够正常运行,验证了系统的可执行性;系统提供了对数据集、特征、算法和集成策略等方面的配置方式,体现了系统的灵活性;更重要的是,利用面向对象技术设计了良好的接口基础,形成一个通用型的集成多标记学习系统框架,反映了系统的可扩展性,可以通过进行二次开发来增强系统功能和提高系统性能,使系统不仅可用于蛋白质亚细胞定位预测问题的求解,还可以用于其他一些多标记学习问题,具有较高的适用性;在给定数据集上得到了较好的实验结果,证明了系统的有效性。在解决诸如蛋白质多亚细胞定位预测等多标记学习问题上,该系统有望成为一个有用的工具并提供一定的参考价值。但系统中还存在着很多需要进一步深入研究的内容,如数据集中样本不平衡问题、蛋白质各亚细胞之间的关联网络和集成策略的设计等。限于未找到在相同数据集上使用其他集成方法的相关文献,目前尚不能把本文的集成方法与其他集成方法进行比较。下一步的主要工作是在更多的特征和数据集上进行实验,与其他集成方法进行比较,进一步验证本文方法的有效性;同时改进现有的学习算法和集成策略,并设计新的学习算法和集成策略,以扩大系统的应用范围。
参考文献:
[1]HANSON M R, KHLER R H. GFP imaging: methodology and application to investigate cellular compartmentation in plants [J]. Journal of Experimental Botany, 2001, 52(356): 529-539.
[2]DREGER M. Proteome analysis at the level of subcellular structures [J]. European Journal of Biochemistry, 2003, 270(4): 589-599.
[3]ZHANG S, XIA X, SHEN J, et al. DBMLoc: a database of proteins with multiple subcellular localizations [J]. BMC Bioinformatics, 2008, 9(1): 127.
[4]CHOU K-C. Some remarks on predicting multi-label attributes in molecular biosystems [J]. Molecular BioSystems, 2013, 9(6): 1092-1100.
[5]CHOU K-C, SHEN H-B. Recent progress in protein subcellular location prediction [J]. Analytical Biochemistry, 2007, 370(1): 1-16.
[6]DU P, LI T, WANG X. Recent progress in predicting protein sub-subcellular locations [J]. Expert Review of Proteomics, 2011, 8(3): 391-404.
[7]CHOU K-C, CAI Y-D. Predicting protein localization in budding yeast [J]. Bioinformatics, 2005, 21(7): 944-950.
[8]GARDY J L, LAIRD M R, CHEN F, et al. PSORTb v.2.0: expanded prediction of bacterial protein subcellular localization and insights gained from comparative proteome analysis [J]. Bioinformatics, 2005, 21(5): 617-623.
[9]DU P, XU C. Predicting multisite protein subcellular locations: progress and challenges [J]. Expert Review of Proteomics, 2013, 10(3): 227-237.
[10]ZHANG M-L, ZHOU Z-H. A review on multi-label learning algorithms [J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819-1837.
[11]NAKASHIMA H, NISHIKAWA K, OOI T. The folding type of a protein is relevant to the amino acid composition [J]. Journal of Biochemistry, 1986, 99(1): 153-162.
[12]CHOU K-C. Prediction of protein cellular attributes using pseudo-amino acid composition [J]. Proteins, 2001, 43(3): 246-255.
[13]CHOU K-C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes [J]. Bioinformatics, 2005, 21(1): 10-19.
[14]SARAVANAN V, LAKSHMI P T V. APSLAP: an adaptive boosting technique for predicting subcellular localization of apoptosis protein [J]. Acta Biotheoretica, 2013, 61(4): 481-497.
[15]ZHANG M-L, ZHOU Z-H. ML-KNN: a lazy learning approach to multi-label learning [J]. Pattern Recognition, 2007, 40(7): 2038-2048.
[16]BOUTELL M R, LUO J, SHEN X, et al. Learning multi-label scene classification [J]. Pattern Recognition, 2004, 37(9): 1757-1771.
[17]FRNKRANZ J, HLLERMEIER E, LOZA MENCA E, et al. Multilabel classification via calibrated label ranking [J]. Machine Learning, 2008, 73(2): 133-153.
[18]READ J, PFAHRINGER B, HOLMES G, et al. Classifier chains for multi-label classification [J]. Machine Learning, 2011, 85(3): 333-359.
[19]TSOUMAKAS G, KATAKIS I, VLAHAVAS I. Random k-labelsets for multilabel classification [J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 23(7): 1079-1089.
[20]SHEN H-B, CHOU K-C. Gpos-mPLoc: a top-down approach to improve the quality of predicting subcellular localization of gram-positive bacterial proteins [J]. Protein & Peptide Letters, 2009, 16(12): 1478-1484.
[21]KENNEDY J, EBERHART R C. A discrete binary version of the particle swarm optimization [C]// Proceedings of the 1997 IEEE International Conference on Computational Cybernetics and Simulation. Piscataway, NJ: IEEE, 1997, 5: 4104-4108.
[22]QU X, WANG D, CHEN Y, et al. Predicting the subcellular localization of proteins with multiple sites based on multiple features fusion [J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2016, 13(1): 36-42.

