地震荷载下土石坝变形分析
薛 逵,付英杰,张永学
(1.普兰店市水土保持办公室,辽宁普兰店116200;2.沈阳经济技术开发区农业发展局,辽宁沈阳110016)
地震荷载下土石坝变形分析
薛 逵1,付英杰2,张永学2
(1.普兰店市水土保持办公室,辽宁普兰店116200;2.沈阳经济技术开发区农业发展局,辽宁沈阳110016)
土石坝在地震荷载下的内部应力应变变化越来越受到重视,针对此问题以辽宁省抚顺市清原县小孤家水库土石坝为例,使用ABAQUS软件,模拟其在地震荷载下的应力应变变化情况,分析计算结果,最后得出该土石坝在此荷载条件下x方向位移和永久变形分布图及加速度变化曲线图,其结果与理论相符,利用ABAQUS软件可以模拟土石坝在实际工程中的受力情况,对于今后土石坝内部应力研究有一定的意义。
土石坝;地震荷载;应力应变;变形分析
0 引言
土石坝是目前世界上建设数量最多的坝型,据国内外建坝数量统计,土石坝占已建坝总数的90%以上,我国的土石坝建设主要集中在20世纪50到70年代。随着近年地震多发,各地的专家开始对于土石坝在地震荷载下的受力及形变情况更加重视。因为在发生地震的时段,含有大片非粘性土料(如砂)的土石坝,在饱和状态下受地震震动时,其强度会降低,从而导致过大的有害位移。受地震破坏的主要原因是土体中的孔隙压力增大,导致土的强度降低而发生液化,是导致垮坝或严重破坏的主要原因。
本文针对以上现象,对大坝观测和现场试验所得到的及时准确的外部数据进行整理和分析,使用ABAQUS软件,应用有限元方法计算出大坝内部的应力应变情况,荷载分布状态。根据有限元法的计算结果、水库水位和坝体土壤层结构模拟地震时土石坝内部孔隙水压力的变化以及坝体内个单元的变形。
1 工程概况
辽宁省抚顺市清原县小孤家水库是一座以城镇供水为主、兼顾灌溉、防洪、水产养殖等中型水利枢纽工程。水库大坝为粘土心墙坝,坝长347.0 m,最大坝高29.5 m,正常蓄水位481.5 m。坝体主要由中粗砂组成,坝壳材料为砂砾料,坝址区基岩为前震旦纪鞍山群变质岩系片麻岩,岩性为角闪斜长片麻岩:暗灰色或灰褐色,中细粒变晶结构,片麻状构造,岩石整体性差,但风化不严重,新鲜岩石较坚硬。第四系冲积层广泛分布于河道两侧、河漫滩、二级阶地之上。岩性自上而下由中细砂和粗砂及部分砾石、卵石组成。主坝基础开挖深3~4 m,底宽5.0 m,建基面为弱风化岩,副坝基开挖深达29 m才见基岩的探坑;坝端处理即坝肩基槽最底盖板高程297 m,顺岩坡到305 m高程,心墙插入岩石的深度一般是1.2~1.4 m,底宽1.5 m。
根据以上地质资料将小孤家水库主坝及坝址区土体和岩石属性分为5种:1)坝前粗砂土;2)坝后中粗砂土;3)心墙粘土;4)坝下强风化岩层,厚度8 m;5)坝下中风化岩层,厚度4 m。
2 计算模型及参数
2.1计算模型
本文应用土的静力有限元计算模型、土的渗流有限元计算模型和土的地震有限元计算模型分别得出土石坝在静力、蓄水和地震3种状态下的受力和形变情况。计算方程如下:
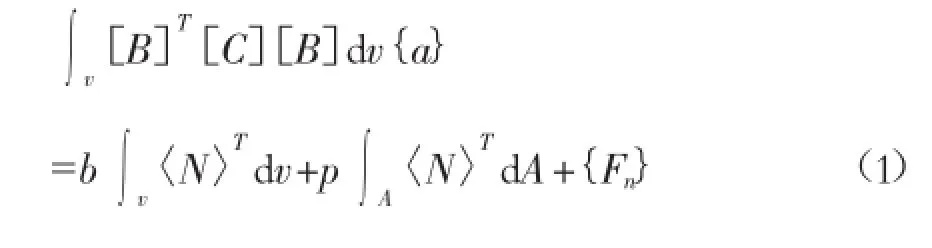
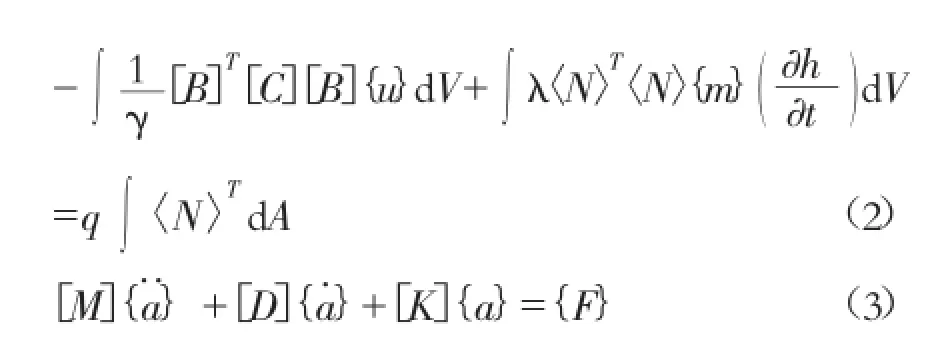
其中:[B]是应变位移矩阵;[C]是本构矩阵;[a]是节点x与y位移增量的列向量;A是沿元素边界的区域;v是单元素体积;b是单位体荷载强度;〈N〉是行向量插值函数;p是表面压力增量;{Fn}是节点集中荷载增量;q为边界节点单位流量;u为孔隙水压力;γ为水的容重;[M]是质量矩阵;[D]是阻尼矩阵;[K]是刚度矩阵;[F]是载体荷载;{·a·}是节点矢量加速度;{·a}是节点矢量速度;{a}是节点矢量位移。
方程(1)为土的静力有限元计算模型,用于计算对于一个给定的时间增量内通过荷载增量产生的位移增量,并将位移增量累积最终得出土石坝各单元的变形值。方程(2)为土的渗流有限元计算模型,它可以得到任意时间段内土体内孔隙水压力变化情况及分布,将方程(1)与(2)耦合分析就能得出土石坝在蓄水状态下各单元的变形值。方程(3)为土的地震有限元计算模型,方程为有限元分析得到的动态响应体系方程,与(1)和(2)耦合分析能够得出土石坝各单元在地震荷载作用下的永久形变。
2.2模型参数
本文选择摩尔-库伦模型为土的本构模型,土石坝计算模型参数由现场取得土样并在实验室内做三轴试验获得,根据固结排水试验结果,计算模型所需参数见表1。
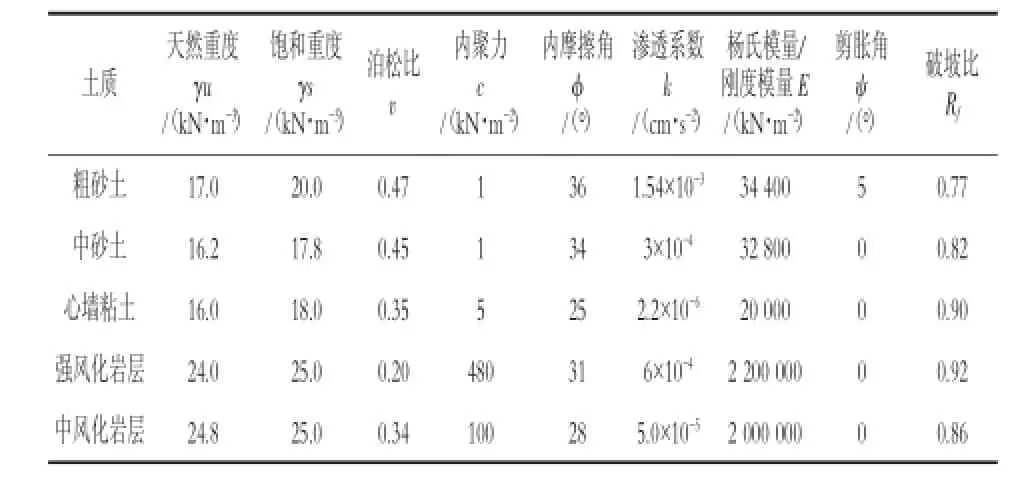
表1 各土层计算参数表
在计算地震荷载作用时,还要引入两组地震加速度时程,两组时程数值相同,但是方向分别是x轴方向和y轴方向。两组时程基准期为100年,超越概率为2%,加速度最大值是116 gal,时程采样间隔0.02 s,持续时间40 s。根据动态周期荷载作用下土体剪切模量随着周期剪切应变的增长而增长的关系,周期剪应变振幅与剪切模量的变化关系可以由G-Reduction函数来表示,由此函数推得动态周期荷载条件下的剪切模量G。由于G随着周期剪应变的增加而减少,区域内应力应变滞后回线所包围的面积增加,导致了阻尼比随着动应变振幅的增加而增加。因此,在动荷载作用下的非线性的剪切模量和阻尼比可以近似地用等效线性分析来模拟,即常数G和阻尼比在动荷载分析中使用,新的模量G和阻尼比在动态分析中通过周期或者等效周期剪应变计算获得。然后,用新模量和阻尼比重新进行动态荷载分析。
3 计算与分析
3.1几何模型建立及其定解条件
本文对小孤家水库土石坝进行二维有限元分析,几何模型所选的是主坝最大断面纵剖面,坝顶最大高程495.5 m,底部中风化层最低高程447.0 m。
此次计算为竣工期,大坝的正常蓄水位为481.5 m,在静力与蓄水状态下,坝下土层侧向水平位移受限制,土层底部水平位移及垂直位移受限制,心墙进入土层部分不做主从面处理,在蓄水状态时心墙迎水面做主从面处理以模拟不透水心墙在水压力及孔隙水压力作用下产生的形变。静力分析时设置作用时间为1 s,时间步长0.025 s;蓄水时设置作用时间为10 s,时间步长0.000 1 s;地震时设置作用时间为40 s,时间步长0.02 s。在地震分析中,将二维有限元分析用一维有限元分析代替,即地震分为两部分,分别导入一组x方向加速度时程A1和一组y方向加速度时程A2。
3.2计算结果
应用ABAQUS对小孤家水库土石坝进行有限元分析,在静力状态下产生的x方向和y方向变形如图1和图2所示,在蓄水状态下产生的x方向和y方向变形如图3和图4所示,在地震荷载作用下产生的x方向和y方向变形如图5和图6所示。
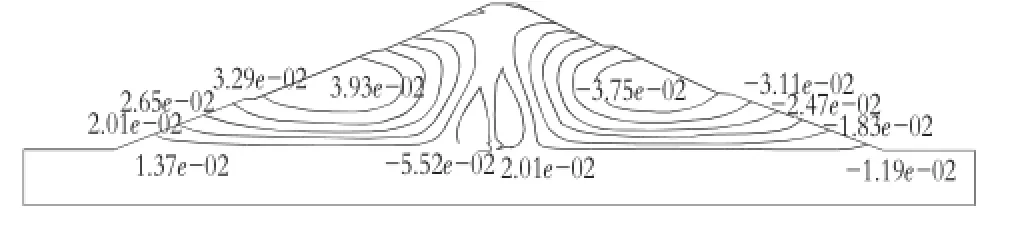
图1 土石坝x方向位移等值线图
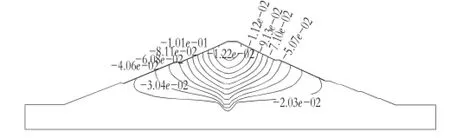
图2 土石坝沉降等值线图
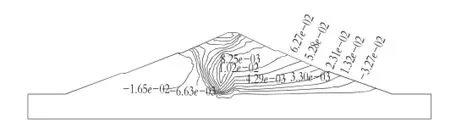
图3 蓄水后土石坝x方向位移等值线图
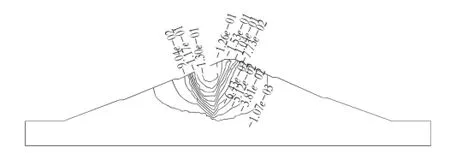
图4 蓄水后土石坝沉降等值线图
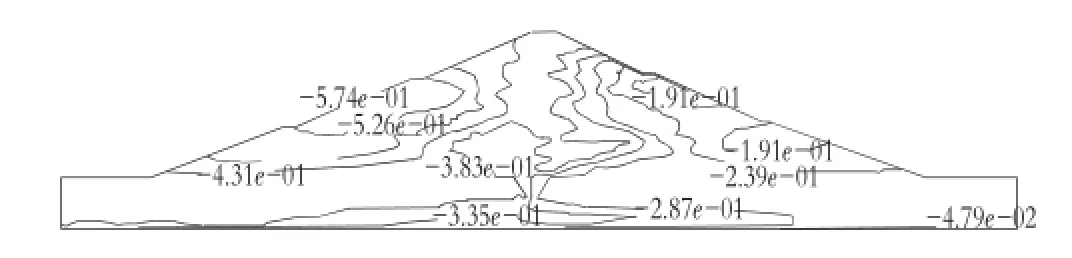
图5 A1条件下土石坝x方向永久变形等值线图

图6 A2条件下土石坝y方向永久变形等值线图
从图1中反映出土石坝迎水坡和背水坡分别产生了向左的3.926 cm最大位移和向右的3.75 cm最大位移,这是由于上面土体下压使得坡面土体向心墙移动符合受力规律。图2中显示土石坝的最大沉降为12.17 cm,位置是在土石坝最上端,出现这种情况的原因是由于小孤家水库土石坝的心墙不是一直修筑至坝顶的,而是与土石坝顶部有0.5 m的空隙,这部分空隙由砂土来填充所以会出现沉降较大的现象。
从图3中可以看到在水库蓄水后土石坝的x方向最大位移为1.02 cm,发生在迎水坡内部。由于孔隙水压力的作用土石坝在x方向上的位移与无水条件下的数据相比有很大的差别,不仅是数值上的改变,在孔隙水压力和浮托力作用下土石坝迎水坡和背水坡x方向位移方向由原来的指向心墙变为与心墙背离方向,并且背水坡最大位移中心由于心墙迎水面受到水压力而向左移动了很多出现在心墙位置。图4中,土石坝最大沉降发生在大坝顶部砂土与心墙的空隙部分,只是由于孔隙水压力和浮托力的作用最大位移中心向左移动了5 m,最大沉降值12.96 cm比无水条件下略有增大。从以上结果可以看出x方向位移的改变最明显,这是由于蓄水后水对土石坝的渗透和冲击作用所导致的,心墙作为不透水面拦截了大部分渗流,同时也承受了较大的水压力使其位移发生显著变化。
在地震荷载作用下土石坝形变改变较大,图5中显示土石坝在A1作用下x方向的永久变形最大值为57.42 cm,位置在迎水坡上,从迎水坡到背水坡变形逐渐减小,最小减至19.14 cm。在图6中,竖向变形主要发生在心墙两侧,最大沉降为34.48 cm在迎水坡面,心墙处沉降为8.41 cm。
在地震荷载计算过程中 40 s内的数据ABAQUS都以表格形式储存,利用此数据可以用来绘制加速度峰值沿心墙轴线随深度变化图。首先将数据中加速度最值选出,然后将分布在心墙轴线上的数据点连成曲线得图7和图8。
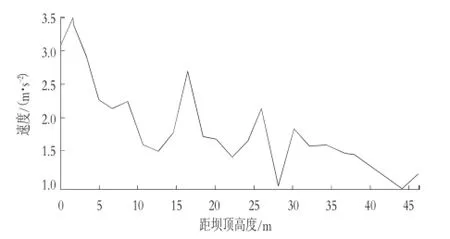
图7 加速度A1峰值沿高度的分布情况
从加速度分分布可以看出,加速度峰值的最大值出现在坝顶部位,土石坝30 m以上加速度变化较大波动明显,30 m以下加速度值程下降趋势且浮动变小。这也说明了砂土相对于风化岩层的不稳定性和易液化性。
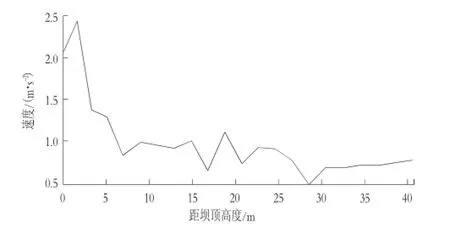
图8 加速度A2峰值沿高度的分布情况
4 结论与展望
4.1结论
本文以摩尔-库伦模型为土体本构模型,采用有限插值法对小孤家水库土石坝进行了有限元分析及计算。计算情况分为静力、蓄水和地震3种:静力部分是为了得到土石坝最初的形态和应力状态,各应力位移的分布情况,为后面的计算分析提供依据和基础数据;蓄水是模拟水库正常运行期间孔隙水压力和浮托力对迎水坡和心墙的影响;地震部分综合了前两步的数据和结果,在给定的加速度时程曲线下分析出土石坝永久变形和加速度分布情况。
通过以上成果不难看出,由于砂土是由土颗粒构成的骨架及空隙中的水和空气组成的,颗粒之间连接较弱,土颗粒骨架具有不稳定性,在静力作用下动力荷载小所以主要表现为弹性变形;在孔隙水压力和循环荷载作用下动应变增大时,本来表现的弹性变形逐渐转变为塑性变形,引起土结构的改变,从而使土的残余变形和强度丧失,尤其对于饱和砂土而言极易发生振动液化。虽然本文研究对象是砂土中相对稳定的中粗砂,但是在结果中可以看到其在静力与动力过程中应力应变和位移的变化程度及波动是非常明显的,甚至发生了位移反向移动的现象。其原因就是在土颗粒中应力是通过触点来传播的,但是在浸水后触点力就要先传递给孔隙中的水,由水来继续承担。这样在循环荷载的作用下,触点力的增加都转化成了孔隙水压力从而引起了孔隙水压力的增加,当孔隙水压力超过静水压力时,就是会使土体的有效应力减少,造成动力抗剪强度降低或者完全丧失,使土发生液化。
综上所述,砂土在静力状态下所表现强度可以满足土石坝安全要求,在动荷载作用下所产生土体性质变化和液化问题应该值得我们注意。在地震多发区建设水工建筑物时应谨慎考虑砂土及类似土型的选用。
4.2展望
在对比验证方面,本文研究的是竣工期水库大坝,所以在能够得到有力验证的沉降方面由于产生沉降值太小没有实现与真实值的对比。希望以后能够以施工期土石坝为研究对象进一步验证模型分析的正确性。也希望能够有更多的研究方法和数据来实现这一目的。
在分析方面,文采用二维方法建模,这种方法只能表现一个断面的数据及形态,但是土石坝是三维立体式的,对于Z方向和XY平面的表现也很重要。在今后的工作中希望能够使用三维建模对水工建筑进行分析计算。
在数据方面,本文中大部分数据来源于现场采样在实验室进行的三轴实验和水库资料数据,由于没有做固结仪实验所以在剪胀角方面是估计值。地震波数据也由于资源有限只采用一组加速度时程曲线来完成整个计算过程。随着近期地震活动频繁,各地接连发生强震并造成大量损失,人们对于地震对于建筑的灾害越来越重视,希望能够有更多数据和研究为今后建筑物抗震提供有效的依据。
[1]孔令伟,郭爱国,陈善雄,等.膨胀土的承载强度特征与机制[J].水利学报,2004(11):54-61.
[2]李广信.高等土力学[M].北京:清华大学出版社,2004.
[3]时卫民,郑颖人.库水位下降情况下滑坡的稳定性分析[J].水利学报,2004(3):67-71.
[4]王厚德.大坝安全监测[C].北京:中国水利水电出版社,2004.
[5]白冰.强夯荷载作用下饱和土层孔隙水压力简化计算方法[J].岩土力学与工程学报,2003,22(9):1469—1473.
[6]米占宽,高面板坝坝体流变性状研究[D].南京水利科学研究院,2001,6.
[7]汝乃华,牛运光.大坝事故与安全·土石坝[M].北京:中国水利水电出版社,2001.
TV698.1+3
A
1002-0624(2016)01-0038-04
2015-02-03

