大地电磁与地震反射波走时数据二维联合反演
陈 霜,谭捍东,高敬语
(1.核工业二〇八大队,内蒙古 包头 014010;2.中国地质大学(北京) 地球物理与信息技术学院,北京 100083)
大地电磁与地震反射波走时数据二维联合反演
陈霜1,2,谭捍东2,高敬语2
(1.核工业二〇八大队,内蒙古 包头014010;2.中国地质大学(北京) 地球物理与信息技术学院,北京100083)
由于地球物理反演存在固有的多解性问题,如何减小多解性,提高地球物理方法反演结果的可靠性和准确性是当今地球物理领域研究的热点。为了减小大地电磁与地震反射波走时资料反演的多解性,在Gallardo和Meju研究的交叉梯度理论的基础上,实现大地电磁与地震反射波走时数据的二维联合反演算法;设计理论地电模型和速度模型进行合成数据的单独反演和联合反演试算,并验证大地电磁和地震反射波走时数据二维联合反演算法的正确性和有效性。反演结果表明,利用交叉梯度方法耦合大地电磁电阻率参数和地震波速度参数能使联合反演过程中的这两个模型在更新的时候相互约束,联合反演结果比单一反演结果更接近真实模型,从而使反演结果更可靠,减少了反演解的多解性。
大地电磁法;地震反射走时;交叉梯度;二维联合反演
0 引 言
地球物理方法可划分为电法、磁法、地震、重力等分支,根据地质体的物性参数不同,可以采用不同的地球物理方法对同一地质体问题进行剖析。但是由于地球物理反演问题存在多解性和不适定性,并且单一的地球物理方法获取的数据往往不能弥补其他物性参数的特点,从而降低了反演结果的可信度,影响反演的可靠性。为了解决这一问题,国内外专家在21世纪初对同一地质体的不同物性参数的联合反演进行了深入的研究[1-13],其中,颇具代表性的是Gallardo和Meju提出的交叉梯度(cross-gradient)法[1-3]。该方法通过在反演的目标函数中加入交叉梯度函数来增加反演过程中对模型的约束,比单一的反演效果更好。近年来,国内学者对联合反演研究也有一定的进展[14-19],如陈晓等在联合反演中引入Tikhonov正则化思想,实现了速度参数和电阻率参数在随机分布情况下的地震资料与大地电磁数据的联合反演研究[19],彭淼等实现了大地电磁和天然地震的三维联合反演算法[17]。联合反演是反演技术发展的必然趋势,许多联合反演实例证明了联合反演效果的优越性[21]。
由于大地电磁探测和地震勘探各自存在着优势和局限,因此联合反演比单一反演更优越[18]。本文通过对地质体电性参数和速度参数的深入了解,开展大地电磁与地震反射波走时数据的联合反演研究,在其反演目标函数中引入模型光滑项、正则化因子和交叉梯度函数,通过设计理论地电模型和速度模型对算法进行有效性试验,来讨论该联合反演方法的可靠性。
1 大地电磁和地震反射波走时二维介质正演理论
1.1大地电磁法二维正演
有限差分(FDTD)法是一种流行的电磁场数值计算方法,已被广泛地应用于求解麦克斯韦方程,具有简洁、直观、计算速度快等优点[26]。大地电磁场满足麦克斯韦方程组:
▽×E=iωμ0H
(1)
▽×H=σE
(2)
▽×B=0
(3)
▽×D=0
(4)
其中:μ0表示地下介质体的磁导率。
在地下介质电阻率是二维分布情况下,大地电磁场可分解为TE和TM两种模式。根据大地电磁响应数据分析,与TE极化模式有关的场分量满足以下场方程[25]:
(5)
(6)
(7)
与TM极化模式有关的场分量满足以下场方程:
(8)
(9)
(10)
给定特定的边界条件,对上述方程组采用有限差分算法进行数值模拟可得到离散节点的场值,按照下面的公式可进一步整理得到视电阻率和相位。
TE极化模式计算公式:
(11)
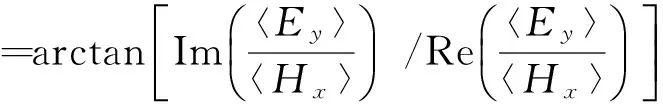
(12)
TM极化模式计算公式:
(13)

(14)
1.2地震反射波走时二维正演
本文中地震反射波走时计算的正演方法采用三点扰动的射线追踪算法[4-7](图1),也叫伪弯曲法[23]。该方法运用Fermat原理,要求对一个初始假设的射线路径不断地进行扰动,直到其满足平稳状态为止。实际上,也就是将沿着射线路径段的走时进行最小化计算,使其达到稳态效果。即利用射线曲率的性质,通过对每一个分段进行最小化计算[22],使其最终的扰动值达到最小。
如图1所示,假设Xk-1和Xk+1是该射线上固定的两个端点,已知Xk-1、Xk、Xk+1是相邻的三个点,从Xk-1到Xk+1,Xk是其一个路径上的初始点,如果有一个新的点Xk′取代点Xk使走时最小化,那么Xk的位置将会被改变。因此,为了寻找这个新的点Xk′,需要得到两个变量,就是从Xk-1、Xk+1中点Xmid出发的偏移量R以及其方向矢量n。方向矢量n可以通过获得反射波最小走时所走的射线路径的弯曲方向得出,然后可以确定R的估计值[20]。
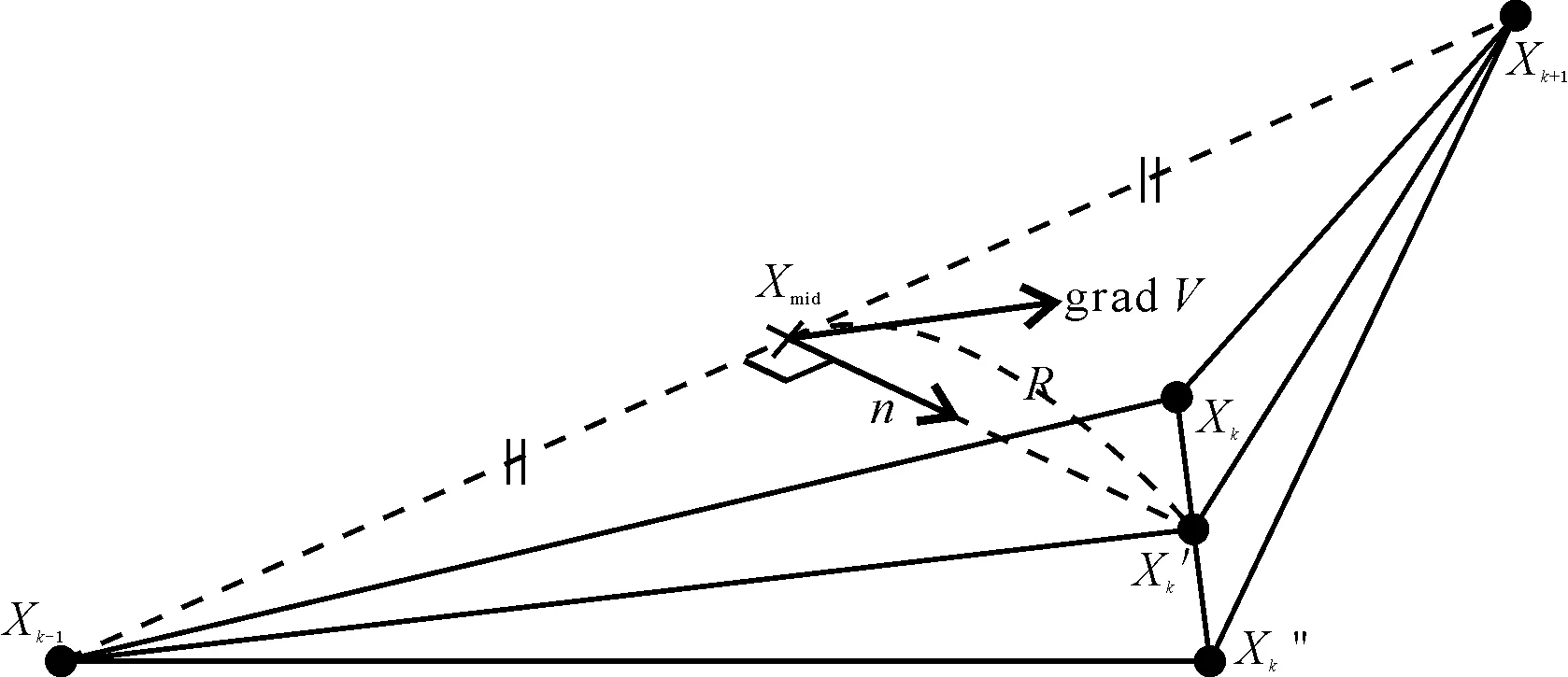
图1 三点扰动方案图解Fig.1 Chart of three-point perturbation scheme
由于新的Xk′点的射线的切线方向与Xk+1-Xk-1的方向近似平行,因此就能得到近似满足方程(15)的点Xk′的偏移方向n′,该方向可表示如下:
n′=(gradV)-[(gradV)·(Xk+1-Xk-1)]。
(15)
通过计算,可以得到该方向的单位矢量n=n′/|n′ |。
新点Vk′的速度可以近似表达式如下:Xk′=Xmid+[n·(gradX)mid]R。
因此,沿着方向n的扰动值满足方程:
Rc=-(cVmid+1)/{4cn·(gradV)mid} +{(cVmid+1)2/
[4cn·(gradV)mid]2+L2/(2cVmid)}1/2
(16)

Xk′=Xk+n′ Rc
(17)
2 交叉梯度联合反演
2.1交叉梯度函数
2003年,Gallardo和Meju首次提出交叉梯度函数的概念[15],本文以地震波速度参数和大地电磁电阻率参数为例,根据交叉梯度原理,得到其三维计算公式如下:
t(x,y,z)=▽mr(x,y,z)×▽ms(x,y,z)
(18)

图2 两种不同物性模型间的交叉梯度计算示意图Fig.2 Charts of cross gradient value for two different property models
式中:▽ms和▽mr分别代表取对数的地震波速度和取对数的电阻率。交叉梯度函数表示的是两种不同物性模型单元参量梯度的叉乘[16]。
交叉梯度具有如下两条特性,如图2所示:
(1)当两种物性参数的其中一种参数为常数或二者的变化方向平行时,交叉梯度值恒等于零;
(2)当两种物性参数朝不相同的方向变化时,交叉梯度值不等于零[14]。
设二维地质体的走向沿y轴正方向延伸,则交叉梯度t的z分量和x分量是零,y分量表达式如下:
(19)
采用五点中心差分网格,将上式用中心差分法离散,得到:
(20)
2.2联合反演目标函数
大地电磁反演的方法较多[24],本文中地震反射波走时与大地电磁数据联合反演算法所采用的目标函数为:

(21)
(22)
(23)
(24)
(25)



i=1, 2, ...,N
(26)
在进行计算的时候,写成矩阵的形式如下:

(27)

图3 联合反演流程示意图Fig.3 Flow chart of the joint inversion algorithm
对电阻率模型求一阶偏导:
(28)
目标函数对速度模型求一阶偏导:
(29)
对(29)式再求二次偏导:
2λ[BMT]TBMT
(30)
因此,得到大地电磁高斯牛顿反演方法的最终迭代方程,即可求得电阻率迭代更新表达式:
(31)
地震波速度最小二乘法反演的最终迭代方程可表示为:
(32)
对应的,也可求出地震波速度更新表达式。
2.3联合反演流程
本文实现大地电磁和地震反射波走时数据联合反演计算的流程如下(图3):
(1)首先设置初始模型。输入初始速度模型v0和初始电阻率模型m0。
(2)最小二乘法实现地震波速度模型更新,计算目标函数梯度gS;求解速度模型扰动量Δvi。
(3)高斯牛顿法实现大地电磁电阻率模型更新[16-17],计算目标函数梯度,求一阶偏导;计算近似Hessian矩阵,求二阶偏导;计算电阻率模型扰动量Δmi。
(4)计算速度模型更新vi+1=vi+Δv和电阻率模型更新ρi+1=ρi+Δρ。
(5)计算地震和大地电磁数据拟合差之和。
(6)判断拟合差之和是否满足目标函数设置的收敛条件。如果不满足,迭代继续,返回步骤(2)重新计算;如果满足收敛条件,完成联合反演程序,跳出迭代,输出反演结果(图3)。
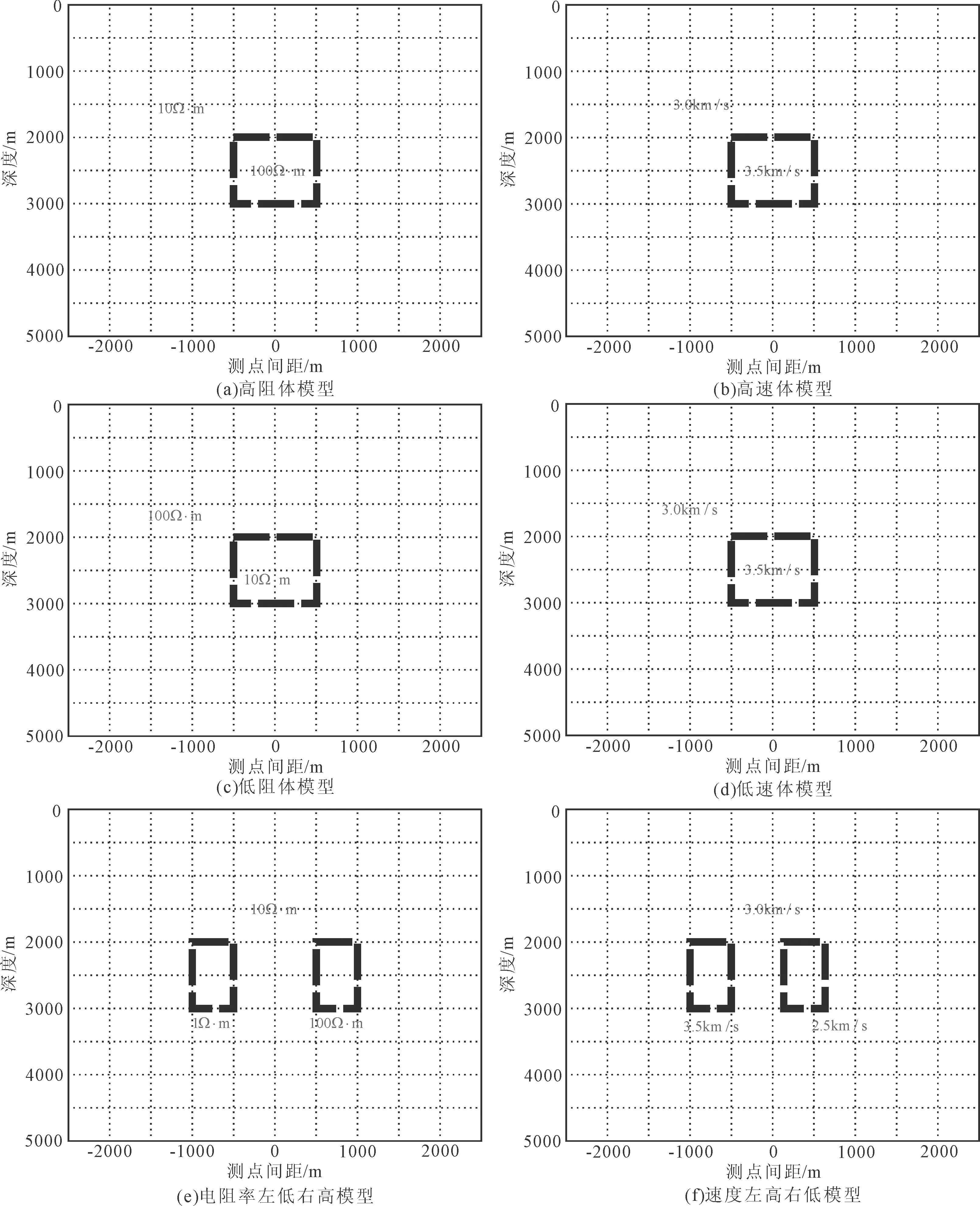
图4 反演理论模型Fig.4 Model for inversion
3 理论模型合成数据算例
在LINUX系统下,利用FORTRAN语言实现大地电磁与地震反射波走时数据的二维联合反演,设计了三个不同的二维模型算例,来验证该算法的正确性和有效性。
3.1单一高阻高速棱柱体模型
设计的第一个模型,电阻率模型与速度模型空间分布一致。大地电磁网格为119×53,网格间距为100m,地震网格为103×53,网格间距也为100m。在此需要说明的是,大地电磁的网格是在地震网格的基础上,水平方向向各自方向分别扩展8个不等间距的网格。
大地电磁模型为高阻体,如图4(a)所示,异常体电阻率值为100Ω·m,背景值为10Ω·m,顶板埋深为2 000m,底板埋深3 000m,宽度1 000m。选取不等间距的25个测点,均分布于地表,频率选取9个,分别为0.010 00Hz、0.050 00Hz、0.100 00Hz、0.500 00Hz、1.00 00Hz、5.00 00Hz、10.000Hz、50.000Hz、100.00Hz。地震反射波走时反演模型为高速体,如图4(b)所示,异常体速度值为3.5km/s,背景值为3.0km/s,顶板埋深为2 000m,底板埋深为3 000m,宽度为1 000m,选取地表的60个激发点,100个接收点。

图5 大地电磁反演结果(电阻率单位:Ω·m)Fig.5 Inversion results for MT data
大地电磁反演的初始模型选取背景值为10Ω·m的均匀半空间,地震反射波走时反演模型选取速度背景值为3.0km/s的均匀半空间,反演迭代20次后,单一反演的结果图分别如图5(a)、图6(a)所示,联合反演结果如图5(b)、图6(b)所示。
从图5(a)、 (b)和图6(a)、 (b)可以看出,联合反演结果比单一反演结果要好。大地电磁联合反演高值恢复较单一反演更接近真实模型,收敛较快,且模型边界光滑度较好;地震联合反演速度高值恢复较好,对异常体外的速度值也有明显的改善。
3.2单一低阻低速棱柱体模型
本文设计的第二个模型,网格剖分同第一个模型。速度异常体与电阻率异常体空间分布一致。

图6 地震波速度反演结果(速度单位:km/s)Fig.6 Inversion results for seismic data
大地电磁模型为低阻体,如图4(c)所示,顶板埋深为2 000m,底板埋深为3 000m,宽度为1 000m,异常体电阻率值为10Ω·m,背景值为100Ω·m,选取不等间距的30个测点,均分布于地表,频率选取9个,分别为0.010 00Hz、0.050 00Hz、0.100 00Hz、0.500 00Hz、1.000 0Hz、5.000 0Hz、10.000Hz、50.000Hz、100.00Hz。地震模型为低速体,如图4(d)所示,异常体速度值为2.5km/s,背景值为3.0km/s,顶板埋深为2 000m,底板埋深为3 000m,宽度为1 000m,选取地表的60个激发点,100个接收点。
大地电磁反演的初始模型选取背景值为100Ω·m的均匀半空间,地震反射波走时反演初始模型选取速度背景值为3.0km/s的均匀半空间,反演迭代30次后,单一反演的结果分别如图5(c)、图6(c)所示,交叉梯度联合反演得到反演结果如图5(d)、图6(d)所示。
从图5(c)、 (d)和图6(c)、 (d)中可以看出,联合反演结果优于单一反演结果,低值异常体都能较好地恢复。大地电磁联合反演结果不仅能恢复电阻率低值,还能对异常体的模型边界有较好的恢复。地震联合反演速度低值恢复地较好,对异常体边界也有明显的改善。
3.3高阻低速、低阻高速棱柱体组合模型
设计的组合模型为分开的低阻高速体和高阻低速体,网格剖分同第一种模型。大地电磁模型左边为低阻体,如图4(e),异常体电阻率值为1Ω·m;右边为高阻体,异常体电阻率值为100Ω·m;背景电阻率值为10Ω·m;顶板埋深为2 000m,底板埋深为3 000m,宽度分别为500m。选取分布于地表的25个测点,频率选取9个,分别为0.010 00Hz、0.050 00Hz、0.100 00Hz、0.500 00Hz、1.000 0Hz、5.000 0Hz、10.000Hz、50.000Hz、100.00Hz。地震模型左边为高速异常体,如图4(f),速度值为3.5km/s;右边为低速异常体,速度值为2.5km/s;顶板埋深为2 000m,底板埋深为3 000m,宽度分别为500m;背景速度值为3.0km/s。选取地表的60个激发点,100个接收点。
大地电磁反演的初始模型选取背景值为10Ω·m的均匀半空间,地震反射波走时的反演模型选取速度背景值为3.0km/s的均匀半空间,反演迭代20次后,单一反演的结果图分别如图5(e)、图6(e)所示。经过联合反演计算,得到的反演结果如图5(f)、图6(f)所示。
从图5(e)、(f)和图6(e)、(f)可以看出,联合反演效果均优于单一反演效果。模型异常能较好地恢复,且反演边界也与模型边界吻合较好。联合反演大地电磁模型中高阻异常体的电阻率与实际值偏差稍大,低阻异常体的电阻率值拟合较好,模型边界恢复也更接近真实模型。联合反演地震模型异常体速度值拟合较好,高速异常体外部高值异常消除,低速异常体低值恢复更好,二者的模型边界较单一反演也有较好的改善。
4 结 论
本文对地震反射波走时和大地电磁数据的二维联合反演进行了较系统的研究,实现大地电磁与地震反射波走时数据的二维联合反演算法。地震方面,基于射线追踪正演算法和最小二乘法反演方法,实现正则化的加入;大地电磁方面,基于有限差分正演算法和高斯牛顿反演方法,实现正反演研究。加入交叉梯度函数后,设计理论地电模型和速度模型进行了合成数据的单独反演和联合反演试算,成功实现了交叉梯度联合反演计算。反演结果表明,联合反演方法优于单一反演方法,利用交叉梯度方法耦合大地电磁电阻率参数和地震波速度参数能使联合反演过程中的这两个模型在更新的时候相互约束、共同影响,使反演结果更接近真实模型,减少了反演解的多解性。本文成果可以为开发其他地球物理方法联合反演算法提供参考。
[1]GALLARDOL,MEJUM.Jointtwo-dimensionalDCresistivityandseismictraveltimeinversionwithcross-gradientsconstraints[J].JournalofGeophysicalResearchSolidEarth, 2010, 109:223-229.
[2]FREGOSOE,GALLARDOL.Cross-gradientsjoint3Dinversionwithapplicationstogravityandmagneticdata[J].Geophysics, 2009, 74(4) :32-41.
[3]HEINCKEB,HOBBSR.JointinversionofMT,gravityandseismicdataappliedtosub-basaltimaging[J].SEGExpandedAbstract, 2006, 25(1) : 784-786.
[4]JUNHOUM,CLIFFORDHThurber.Afastalgorithmfortwo-pointseismicraytracing[J].BulletinofTheSeismologicalSocietyofAmerica, 1987,77(3) :972-986.
[5]CLIFFORDHThurber.Improvedthree-dimensionalvelocitymodelsandearthquakelocationsforCalifornia[J].JournalofGeophysicalResearch, 2003,108(2):1029-2002.
[6]CLIFFORDThurber,DONNAEberhart-Phillips.Localearthquaketomographywithflexiblegridding[J].Computers&Geosciences, 1999,25(7) : 809-818.
[7]ROECKERC,THURBERD,MCGHEED.Jointinversionofgravityandarrivaltimedatafromparkfield:newconstraintsonstructureandhypocenterlocationsneartheSAFODdrillsite[J].GeophysicalResearchLetters, 2004, 31(12):399-420.
[8]于鹏,戴明刚,王家林,等. 电阻率和速度随机分布的MT与地震联合反演[J]. 地球物理学报, 2009, 52(4):1089-1097.
[9]杨辉,王家林,吴健生,等. 大地电磁与地震资料仿真退火约束联合反演[J]. 地球物理学报, 2002,45(5):723-734.
[10]MEJUMA,GALLARDOLA,MOHAMEDAK.Evidenceforcorrelationofelectricalresistivityandseismicvelocityinheterogeneousnear—surfacematerials[J].GeophysicalResearchLetters, 2003,30(7) :1373-1376.
[11]陈晓,于鹏,张罗磊,等. 地震与大地电磁测深数据的自适应正则化同步联合反演[J]. 地球物理学报, 2011,54(10):2673-2681.
[12]林昌洪,谭捍东,佟拓.大地电磁面积性资料和稀疏测线资料的三维反演解释[J].现代地质,2012,26(6):1185-1192.
[13]JEGENMD,RICHARDWH,PASCALT,etal.Jointinversionofmarinemagnetotelluricandgravitydataincorporatingseismicconstraints-preliminaryresultsofsub-basaltimagingofftheFaroeShelf[J].EarthandPlanetaryScienceLetters, 2009, 282(1):48-53.
[14]彭淼,谭捍东,姜枚,等. 基于交叉梯度耦合的大地电磁与地震走时资料三维联合反演[J]. 地球物理学报, 2013,56(8):2728-2738.
[15]GALLARDOLA,MEJUMA.Jointtwodimensionalcrossgradientimagingofmagnetotelluricandseismictraveltimedataforstructuralandlithologiealclassification[J].Geophysicaljournalinternational, 2007,169(3):1261-1272.
[16]周丽芬. 大地电磁与地震数据二维联合反演研究[D].北京:中国地质大学(北京),2012:7-36.
[17]彭淼.大地电磁与天然地震数据联合反演研究[D] .北京:中国地质大学(北京), 2012:25-47.
[18]刘彦,吕庆田,孟贵祥,等. 大地电磁与地震联合反演研究现状与展望[M]. 地球物理学进展, 2012,27(6):2444-2451.
[19]陈晓,于鹏,张罗磊,等. 大地电磁与地震正则化同步联合反演[J] . 地震地质, 2010,32(3): 402-408.
[20]张美根,程冰洁,李小凡,等. 一种最短路径射线追踪的快速算法[J] . 地球物理学报, 2006,49(5):1467-1474.
[21]王俊,孟小红,陈召曦,等. 交叉梯度理论及其在地球物理联合反演中的应用[J]. 地球物理学进展, 2013,28(4):2094-2013.
[22]CLIFFORDHThurber.Earthquakelocationsandthree-dimensionalcrustalstructureintheCoyoteLakeArea,centralCalifornia[J].JournalofGeophysicalResearch, 1983, 88(10):8226-8236.
[23]郭继茹,冯晅,王俊祥,等. 最佳路径射线追踪算法研究[J]. 吉林大学学报(地球科学版),2008,38(1):72-76.
[24]谭捍东, 陈乐寿,魏文博,等. 先进的大地电磁资料处理和反演方法在INDEPTH-MT中的应用研究[J]. 现代地质, 1997,11(3):393-400.
[25]谭捍东, 魏文博,陈乐寿,等. 大地电磁标定曲线的畸变及校正[J]. 现代地质, 1998,12(4):603-606.
[26]林树海,王伟利. 电磁波场数值计算中时间域有限差分法与时间域伪谱法的对比研究[J]. 现代地质, 2012, 26(6):1193-1198.
附公式中变量说明:
μ0,地下介质体的磁导率;E,电场强度;D,电位移矢量;B,磁感应强度;H,磁场强度;▽ms,取对数的地震波速度;▽mr,取对数的电阻率;σ,介质的电导率;ρ,电阻率;φ,相位;ω,角速度。
Ex,x方向电场强度;Ey,y方向电场强度;Ez,z方向电场强度;Hx,x方向磁场强度;Hy,y方向磁场强度;Hz,z方向磁场强度;mr,电阻率值;ms,速度值。


Two-dimension Joint Inversion of Magnetotelluric and Seismic Reflection Travel Time Data
CHEN Shuang1,2, TAN Handong2, GAO Jingyu2
(1.GeologicalExplorationPartyNo.208,CNNC,Baotou,InnerMongolia014010,China;2.SchoolofGeophysicsandInformationTechnology,ChinaUniversityofGeosciences,Beijing100083,China)
Because of the problem of multiple solutions for geophysical inversion, how to reduce the multiple solutions to improve the reliability and accuracy of the results of geophysical inversion is a hot geophysical research topic today. To reduce the multiple solutions of magnetotelluric and seismic data inversion, this study develops a 2-D joint inversion algorithm of magnetotelluric data and seismic data on the base of cross-gradient theory which is proposed by Gallardo and Meju, and the theoretical geoelectric model and velocity model are designed for single inversion and joint inversion, then the 2-D joint inversion algorithm of magnetotelluric and seismic data is verified to be correct and valid. The inversion results show that the above inversion algorithm with cross-gradient constraints can cause the resistivity model and velocity model constrain each other so that the joint inversion result is closer to the reality than the single inversion result. Therefore, the joint inversion is more reliable, which can reduce the multiple solution of geophysical inversion.
magnetotelluric method;seismic reflection travel time;cross-gradient method;2-D joint inversion
2015-09-14;改回日期:2016-05-05;责任编辑:潘令枝。
国家自然科学基金项目(41374078);国土资源部地质调查项目(12120113086100,12120113101300)。
陈霜,女,硕士研究生,工程师,1985年出生,地球物理学专业,主要从事地球物理地电学算法研究工作。Email:chens130@163.com。
谭捍东,男,1966年生,教授,地球探测与信息技术专业,主要从事电法勘探理论及应用研究。
Email:thd@cugb.edu.cn。
P631
A
1000-8527(2016)03-0597-09

