基于自适应滤波法的静电传感器转速测量

唐凯豪,胡红利,李　林,李思瑶,张　肖,2

(1.西安交通大学 电力设备电气绝缘国家重点实验室,陕西 西安　710049；2.西安市产品质量监督检验院 线缆室,陕西 西安　710065)



基于自适应滤波法的静电传感器转速测量

唐凯豪1,胡红利1,李林1,李思瑶1,张肖1,2

(1.西安交通大学 电力设备电气绝缘国家重点实验室,陕西 西安710049；2.西安市产品质量监督检验院 线缆室,陕西 西安710065)

为解决使用静电传感器进行信号自(互)相关转速测量中，因信号干扰大导致相关法时延计算易出错的问题，采用自适应滤波算法对相邻传感器的时延信息进行提取,从而达到测速的目的。实验结果表明，该方法能有效得出测速结果,并对叠加了强噪声的静电信号也有良好的表现。对异步电机转轴进行测试,转速测量的线性度达到1.29%,具备一定的应用价值。

自适应滤波;静电传感器;转速测量;降噪

TH824.1；TP274.5

A

10.16152/j.cnki.xdxbzr.2016-04-006

转速是旋转机电设备运行控制和状态监测的重要参数,其测量方法一直是研究的热点。近几年,闫勇、王丽娟[1-3]等学者采用的静电法转速测量以其非接触、低成本、抗恶劣环境等特性而受到关注。静电法测速的实质是获取旋转物体表面某点从一个位置到另一个位置的渡越时间,以此计算转速[2]，其关键在于时延获取。

而静电信号常常叠加了强噪声,已有学者提出的自(互)相关算法常导致计算失败,其主要原因是时延信息淹没在周期性噪声中。基于自适应滤波的时延估计已被应用于雷达探测[4]、多相流流速测量[5-7]等领域,对于强噪声信号有很好的处理能力。

基于以上研究，本文对已有的静电传感器转速测量原理进行算法改进,探索采用自适应滤波法进行转速计算的可行性。

1　改进的静电传感器转速测量原理

1.1静电传感器转速测量原理

旋转设备运行过程中,旋转表面因与空气持续摩擦而带上电荷,并且电荷会不断产生和流失。由于旋转面带电的随机性,安置在旋转表面周围的静电传感器(不与表面接触)能感受旋转面电荷量的变化而产生随机的静电信号。信号类似于噪声，因为旋转面的周期性运动而带有明显的周期性[2]，如图1所示。安装在转轴周围的传感器由于空间位置排布的相差角度为α，不同传感器的两路信号具有明显时延t,即旋转面经过上、下游传感器的渡越时间,如图1所示。

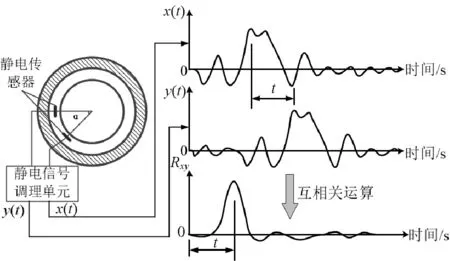
图1　静电传感器位置及波形示意图Fig.1　Installation location of electrostatic sensors and the output waveform

设数据采集卡采样频率为f，则两传感器间信号时延可由式(1)得出

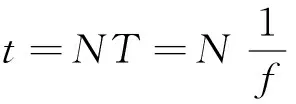
(1)

式中，N表示一路信号超前(或滞后)另一路信号的采样点数。

由此可得转速w为

(2)

由于f，α均为已知量，转速测量问题就转化为上、下游传感器信号延时点数N的获取问题。

1.2基于LMS算法的横向自适应滤波时延估计原理

自适应滤波器是一种能够自动调节本身参数(权系数矢量W(n))的特殊滤波器。在设计时不需要事先知道输入信号和噪声的统计特性，这些特性能够在工作过程中逐渐被估计出，并以此为依据自动调整自己的参数,以达到某种最佳准则的要求。

一种普遍使用的准则是最小均方误差(Least mean square,LMS)准则[8],基于LMS算法的有限冲击响应(Finite impulser response,FIR)自适应滤波器如图2所示。

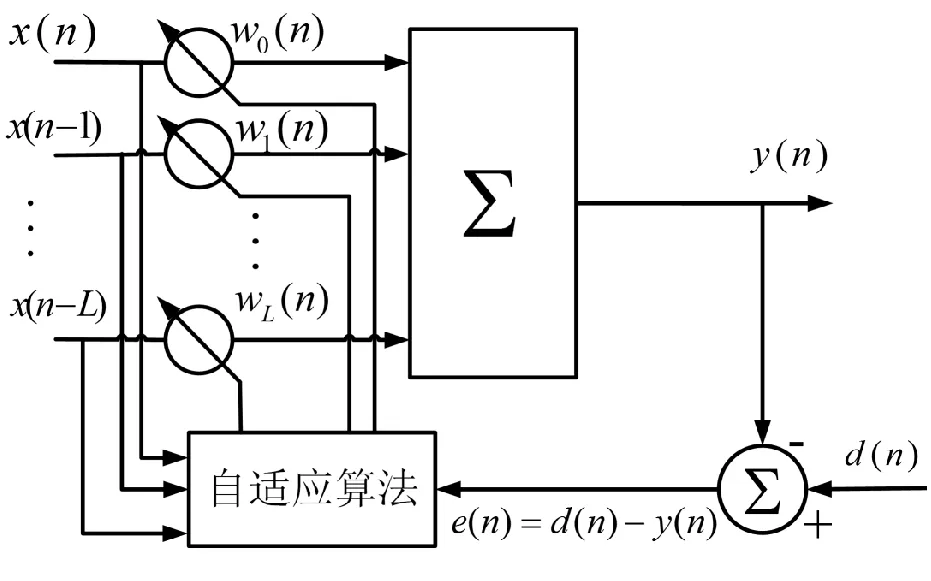
图2　 L阶加权自适应横向滤波器Fig.2　L-order weighted adaptive transversal filter

设x(n)和y(n)分别为上、下游传感的输出,滤波器权系数为

W(n)=[w0(n),w1(n)，…，wM-1(n)]T。

式中:M为滤波器模型阶次。

滤波器输入信号为

X(n)=[x(n)，x(n-1)，…，x(n-M+1)]T，

滤波器输出为

Y(n)=WT(n)X(n)=

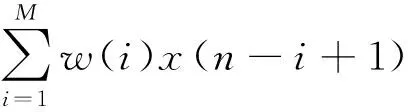
误差信号为

e(n)=y(n)-Y(n)=

y(n)-XT(n)W(n)。

根据维纳滤波器理论[9]，自适应滤波器收敛时权系数矢量W(n)取得维纳解[9],此时的权系数矢量Wopt收敛于wL(n)，该分量为Wopt全部分量中的最大值,其序数L即为延时点数。

至此,LMS算法可描述为:

1) 初始化:令所有权重的初值wi(1)(i=0,1,…,M-1)为任一固定值或0,对每一个接下来的抽样时刻k(k=1,2,…,N)执行步骤2)～4)。

2) 计算滤波输出，

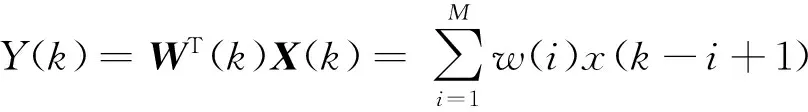
3) 计算误差，

e(k)=y(k)-Y(k)。

4)计算下一时刻新的权系数矢量，

w(k+1)=w(k)-2μe(k)x(k)。

从以上过程可以看出,LMS算法对每组输入和输出抽样大约需2N-1次乘法和2N-1次加法。大多数信号处理器都适宜进行乘法和累加运算,使直接实现LMS算法更具有可操作性。

2　实验结果与分析

2.1实验平台

实验平台如图3所示,平台上为电机传动系统。装置运作时,通过变频器控制电机正、反转以及转速，电机通过传动皮带带动被测转轴运动。转轴装有屏蔽罩,整个实验平台接地。

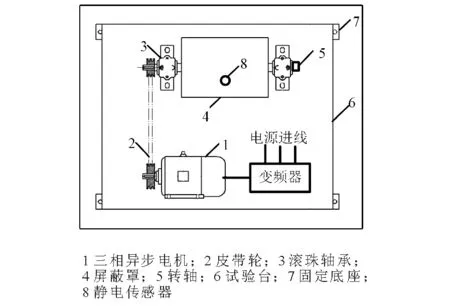
图3　实验平台示意图Fig.3　 Experiment platform

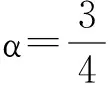
设置记录仪采样频率为5kHz,记录时长20s,重复进行10次实验,即记录10段数据。根据记录的数据,计算测量转速,记为RPMm,并拟合“参考转速测量转速”曲线,分析自适应滤波计算转速的重复性、线性度、测量范围。

实际上，电机转速变化滞后于变频器频率变化,但考虑到滞后时间是一固定常数,故该滞后时间不影响拟合结果的线性度。

处理数据时,将原始数据细分为2 000点/段,共计50段,每段内速度视为恒定,采用1 100维自适应滤波器进行运算，取每段内中间时刻理论速度作为该段的参考转速。

2.2测量范围

上、 下游传感器原始信号(以转速为2 600r/min时为例)如图4所示。

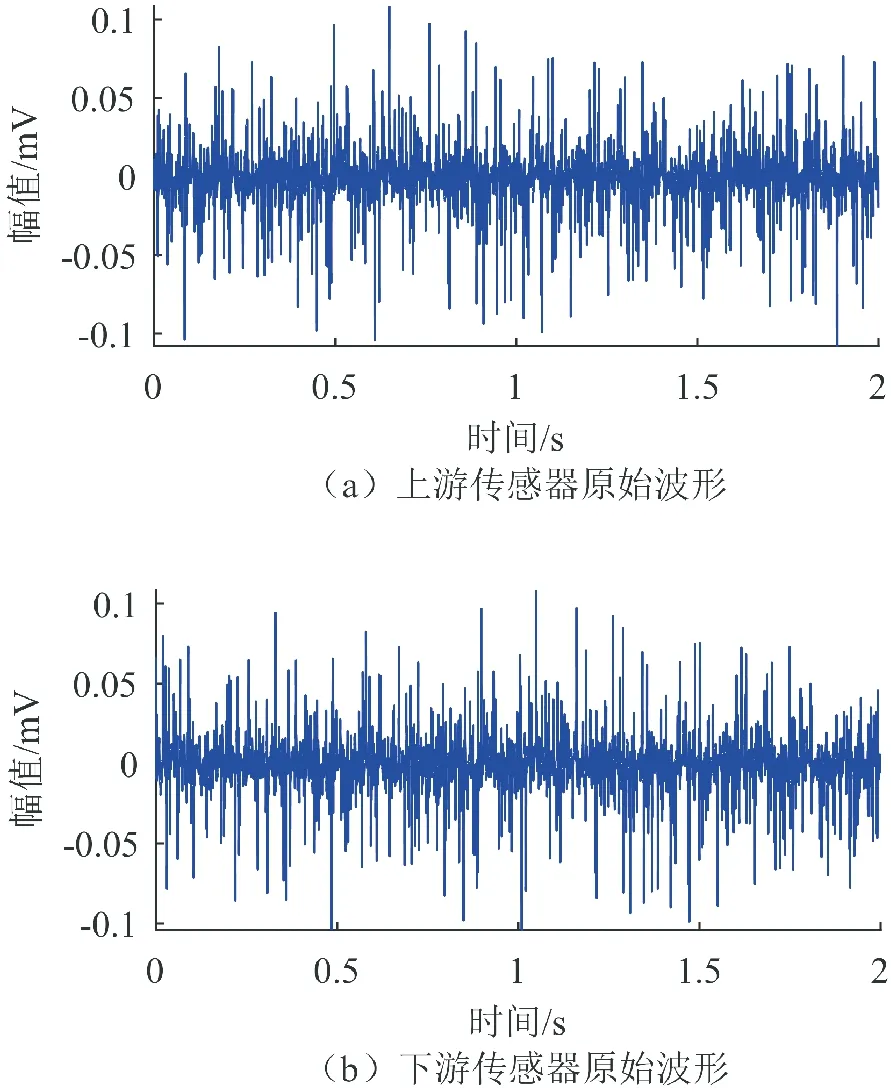
图4　转速为2 600r/min时上、下游传感器原始信号Fig.4　Original output signals of upstream and downstream sensors under rotational speed of 2 600r/min

上述两路信号经自适应滤波运算后得到最佳权系数矢量Wopt波形如图5所示。

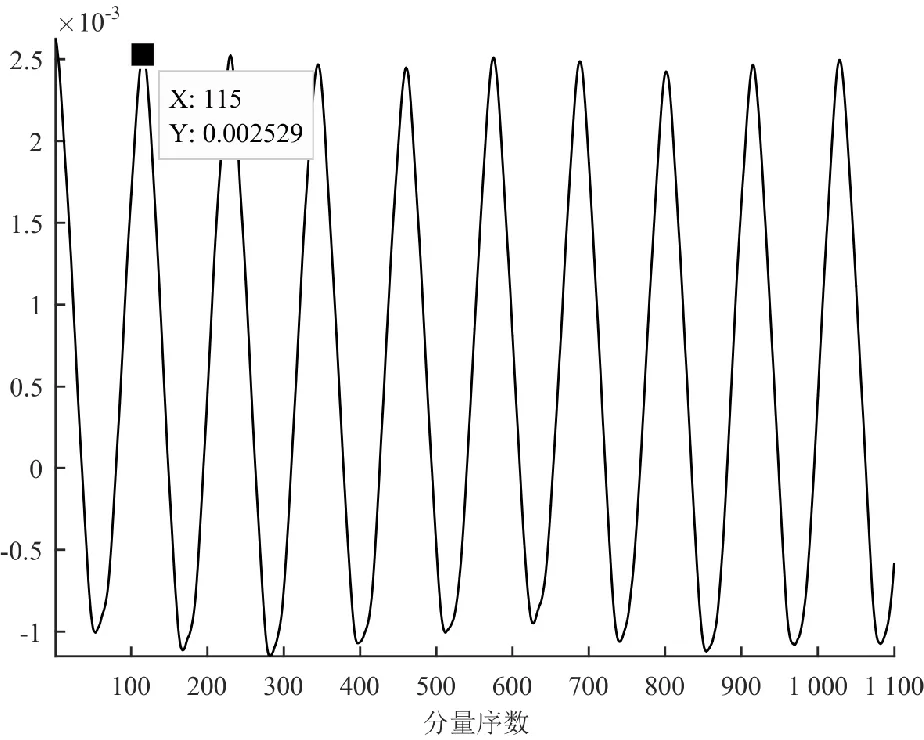
图5　转速为2 600 r/min时最佳权系数矢量波形Fig.5　Optimum weight vector waveform under rotational speed of 2 600 r/min

由图5中最佳权系数矢量最大分量的序数(115)即可得到时延信息,由此可计算出整个过程的转速变化曲线,如图6所示。

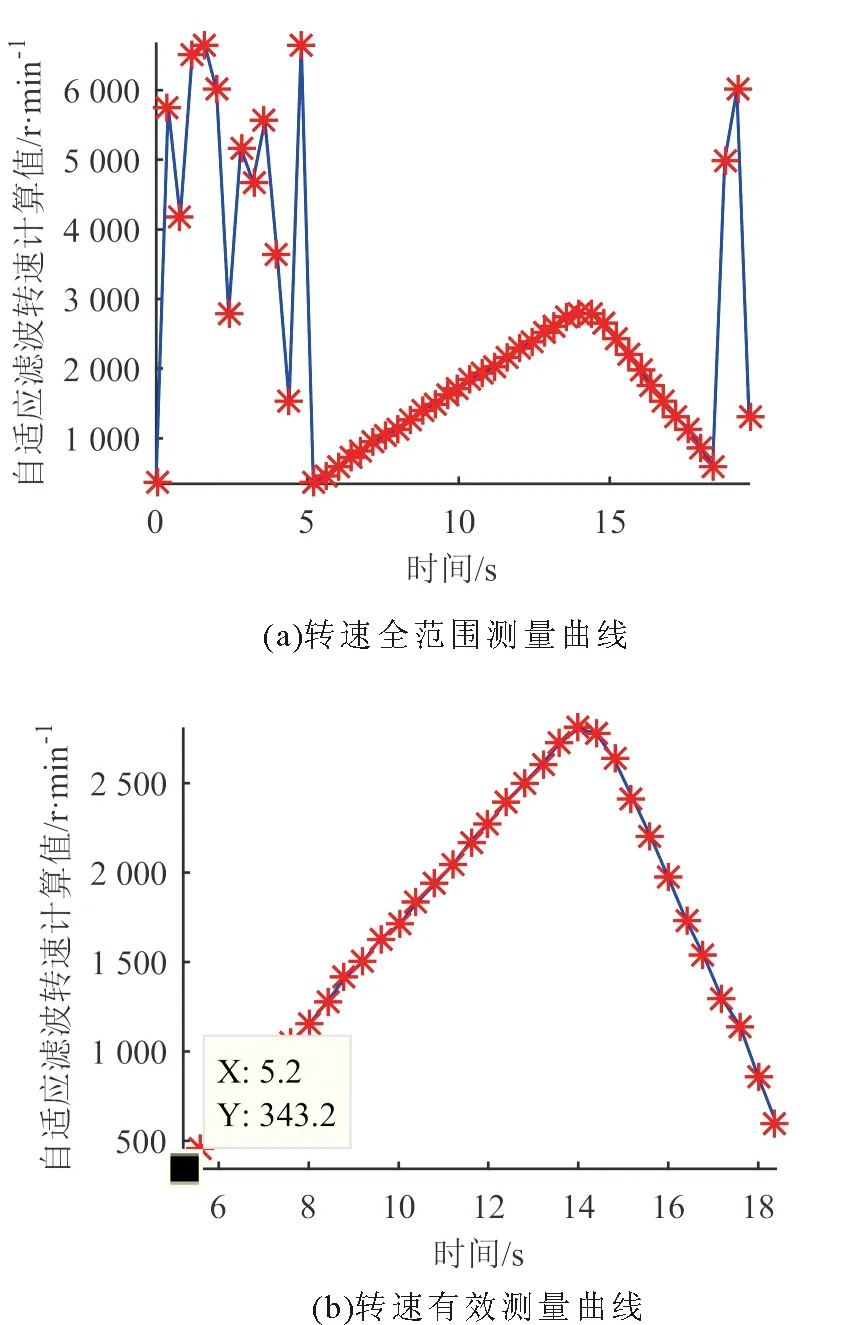
图6　实验装置转速变化曲线Fig.6　Rotational speed change curve of experiment device

从图6(a)中不难发现,在小转速情况(转速≤343r/min)时,转速计算失败,这是因为转速很小时,两路传感器的周期性噪声幅值相对信号来说很大,影响自适应滤波的计算,使计算得到的时延并非信号时延, 而是噪声的广义相关运算[10]结果。 因此本次实验中有效测量范围为343～3 000r/min。

2.3线性度

在有效测量范围内,计算得到RPMm与RPMr的部分数值如表1所示。

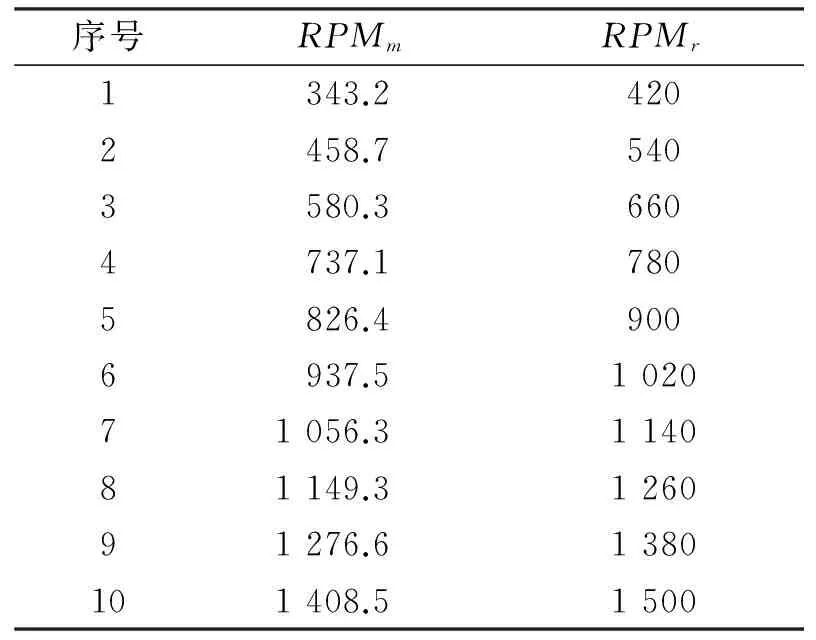
表1　部分计算数据

根据误差理论,计算可得匀加速阶段线性度为1.29%,匀减速阶段线性度为2.51%,均在5%以内。

对有效测量范围内的点进行线性拟合,可得拟合曲线如图7所示。拟合曲线的表达式为

加速:RPMr=1.067 3RPMm+25.871 7，

(3)

减速:RPMr=1.095 4RPMm-409.301 0。

(4)

可见,自适应滤波算法测量转速能很好地对平稳加速度进行跟踪。

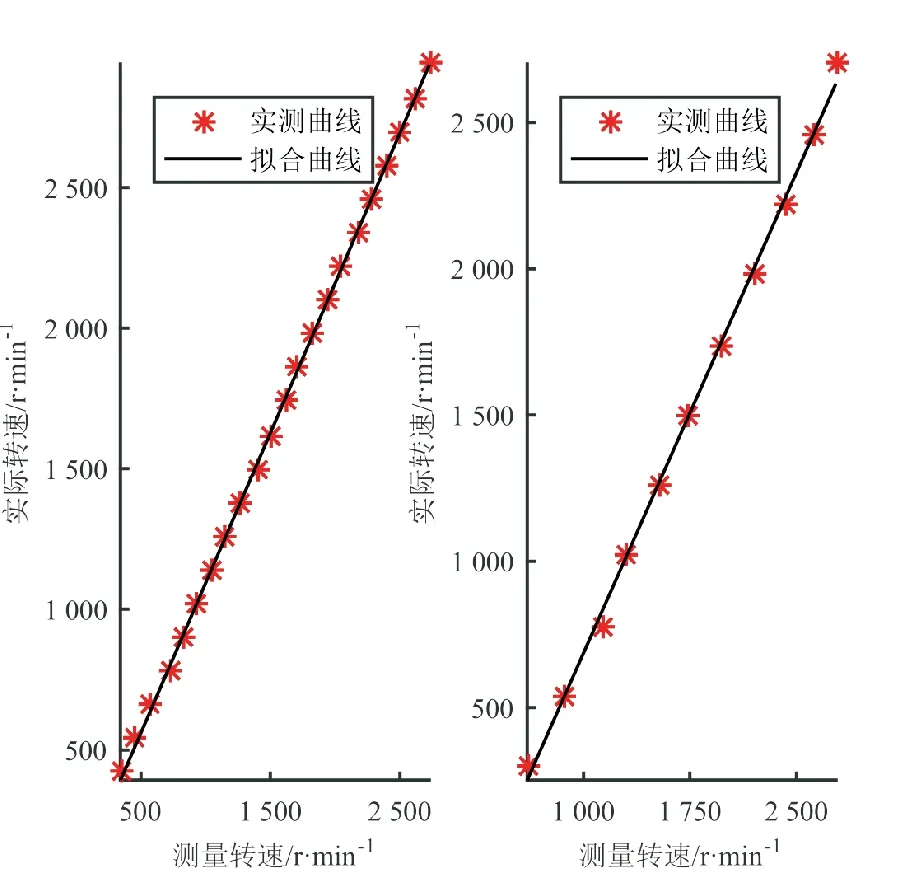
图7　自适应滤波转速计算拟合曲线Fig.7　Fitting curve of rotational speed computied by the adaptive filter

在减速阶段拟合的线性度不如加速阶段理想,这是由于在采样频率不变的情况下,加速度更大时，数据段需要更细地划分;而数据段更窄，则要求滤波器维数更小,所以能测量的转速下限越高。

3　总结与展望

在实验平台进行的实验表明,自适应滤波法转速测量,能对343～3 000r/min范围内转速进行准确测量,该方法的线性度为1.29%。

由式(3)、式(4)可知,该测试系统能很好地跟踪平稳加速度。此外,由测速原理和实验结论可得出，对大加速度、高转速的设备进行转速监测时需满足下述两个条件之一:

1) 在采样频率不变的情况,若对大加速度的设备进行转速跟踪,需要更窄的数据段和与数据段长度相匹配的滤波器维数,同时要求设备运行转速较高，否则会导致计算失败。

2) 若维持数据段长度不变,必须提高数据采集设备的采样频率,否则也会导致计算失败。

数据段长度的选取和滤波器维数的设计需要依托一定经验,其定量规律还需要进一步探究。

[1]WANG L J, YAN Y, HU Y H, et al. Intelligent condition monitoring of rotating machinery through electrostatic sensing and signal analysis[C]∥2013 IEEE International Conference on Smart Instrumentation, Measurement and Applications. IEEE, 2013:1-4.

[2]WANG L J, YAN Y, HU Y H, et al. Rotational speed measurement through electrostatic sensing and correlation signal processing[J].IEEE Transactions on Instrumentation and Measurement, 2014, 63(5): 1190-1199.

[3]WANG L, YAN Y. Mathematical modeling and experimental validation of electrostatic sensors for rotational speed measurement[J]. Measurement Science and Technology, 2014, 25(11): 115101.

[4]李雪梅,陶然,王越.时延估计技术研究[J].雷达科学与技术,2010,8(4):362-371.

[5]张 岩，牛跃华，彭黎辉，等.基于自适应滤波的气/固两相流固体颗粒速度测量方法[J].仪器仪表学报,2007,28(11):1927-1931.

[6]邢文奇,胡红利,董军.采用互相关与自适应滤波算法测量流速的比较研究[J].西安交通大学学报,2011,45(6):111-115.

[7]赵浩亮.基于LMS自适应时延估计和ARM的三相流流量测量系统研究[D].秦皇岛：燕山大学,2014.

[8]HAYKIN S. Adaptive Filter Theory[M].Canada: Prentice Hall,2013:248-266.

[9]迪尼.自适应滤波算法与实现[M].北京:电子工业出版社，2004：3-7,24-26.

[10] 杜鹃,程擂.基于二次相关的时延估计方法研究[J].弹箭与制导学报,2010,30(6):221-223.

(编辑李静)

Rotational speed measurement using an electrostatic sensor and based on a electrostatic signals processing method of adaptive filter

TANG Kai-hao1, HU Hong-li1, LI Lin1, LI Si-yao1, ZHANG Xiao1,2

(1.State Key Laboratory of Electrical Insulation and Power Equipment, Xi′an Jiaotong University, Xi′an 710049, China; 2.Xi′an Supervision & Inspection Institute of Product Quality Cable Compartment, Xi′an 710065， China)

Rotational speed measurement using an electrostatic sensor and signals correlation is a novel method put forward recently, but speed calculation fails sometime due to strong noise added in signals.In this research,a signals processing method of adaptive filter is discussed and used to extract the time-lag between an adjacent pair of signals in order to calculate the rotational speed.The result of the experiment carried out indicated that the method mentioned above had a reliable performance in term of accuracy even when handling signals with heavy noise component; linearity of the measurement tested on a laboratory-scale test rig is 1.29%, which has a possibility of putting into industries.

adaptive filter; electrostatic sensor; rotational speed measurement; noise reduction

2015-10-25

国家自然科学基金资助项目(51177120)；西安交通大学电力设备电气绝缘国家重点实验室主任基金资助项目(EIPE14132)；陕西省工业科技攻关计划基金资助项目(2016GY-001)

唐凯豪，男，江苏江阴人，西安交通大学博士生，从事电磁计量传感器与信号处理技术研究。