基于链表结构的启发式属性约简算法

梁 宝 华

(巢湖学院计算机与信息工程学院　安徽 合肥 238000)



基于链表结构的启发式属性约简算法

梁 宝 华

(巢湖学院计算机与信息工程学院安徽 合肥 238000)

属性约简是粗糙集理论研究的主要内容之一，正区域计算是多数属性约简算法的关键。为了减少正区域的计算时间，提出基于链表存储的正区域计算方法。将属性值相同的数据存储在链表同一结点对象中，收集过程中不断删除基数为1的子划分，通过降低样本数据的规模来减少计算耗时，加速属性约简。同时，给出不可区分对象对数定义，并以此度量属性重要性，设计一种高效的启发式属性约简方法。通过实例和实验与经典约简算法进行性能测试比较，结果证实该算法在时间和空间效果上切实有效、可行。

粗糙集属性约简链表正区域不可区分对象对数

0　引　言

RoughSet作为一种处理不确定、不精确数据的有力数学工具[1]，已广泛应用于机器学习、模式识别和数据挖掘等领域。属性约简是RoughSet研究的核心问题之一，也是知识获取的关键步骤。在保持区分能力不变的情况下，用较少属性表示数据集的特征。现有的属性约简算法有基于正区域属性约简算法[2]、基于信息熵的约简算法[3]、基于差别矩阵的属性约简算法[4,5]及其他启发式属性约简算法[6,7,12]。

多数属性约简算法先对挖掘的决策表进行简化，因为此过程效率高低影响整个算法的时间和空间性能。目前，求简化决策表效率较高的算法有文献[2]基于基数排序的属性约简算法，时间复杂度为O(|C‖U|)、基于文献[8]快速排序思想的属性约简算法，时间复杂度为O(|C‖U‖log(U)|)。为了更进一步缩短求解简化决策表时间，本文提出基于链表结构的快速求正区域方法，比文献[2]的算法效率略有提高。在求解属性约简过程中，本文采用不可区分对象对数的函数，作为衡量属性重要性的依据，既达到差别矩阵算法的直观性、易理解性的优点，又避免了差别矩阵需大量空间存储信息矩阵的缺点，提高了时间和空间处理效率。

1　相关概念

定义1一个信息系统IS=(U,A,V,f)，其中U为所有挖掘对象的集合；A是所有属性的集合，A=C∪D，C为条件属性集，D为决策属性集，V为全体属性的值域集，f为U×A→V的信息函数，定义f(x,a)为x在属性a上的对应值。若P⊆A，则不可分辨关系为：

IND(P)={(x,y)∈U×U|∀a∈P,f(x,a)=f(y,a)}，构成U的一个划分用U/IND(P)。

定义2给定决策表T=(U,A,V,f)，对于任意子集X⊆U和不可分辨关系IND(P)：

下近似：

(1)

上近似：

(2)

定义3决策表T=(U,A,V,f)中，P⊆C，D的P正区域记为：

(3)

定义4决策表T=(U,A,V,f)中，P⊆C，D的P负区域记为：

NEGP(D)=U′-POSP(D)

(4)

其中U′为简化后的无重复数据。

定义5[4]在简化决策表T′=(U′,C,D,V,f)中，决策表的分明矩阵(简称简化分明矩阵)M′=mi,j，其元素定义如下：

(5)

性质1设P⊆C,|U/Pi|=1，则U/Pi中的元素均属于正区域POSP(D)。

证明：由IND(P)定义可知，若x1∈U,x2∈U∧f(x1,P)=f(x2,P)，则x1、x2属于同类划分，若f(x1,D)=f(x2,D)，则由POSP(D)定义可知，x1、x2属于正区域元素，否则，属于负区域元素。因为|U/Pi|=1，所以，U/P的第i个划分中只有一个元素，设此元素为x。假设x属于负区域，则可找到另一元素y，使得f(x,P)=f(y,P)且f(x,D)≠f(y,D)，但x∈U/Pi∧|U/Pi|=1，说明f(x,P)是唯一的，所以上述假设不成立，故x必属于正区域元素。证毕。

2　快速计算正、负区域算法及其分析

2.1快速求正、负区域算法(算法1)

属性约简过程，大体进行三步：(1) 数据预处理，将数据离散化；(2) 将决策表简化(可得到相应的正、负区域)；(3) 属性约简。由此可知，简化决策表是属性约简过程的关键环节。若能得到有效的简化决策表，可减少约简的搜索空间。为了快速、有效得到简化决策表，很多学者做了相关研究，效果较好的有文献[2,6]。其中，文献[2]的基数排序算法每次对数据收集时未能将已区分对象进行剪枝，后期约简未能充分利用前期结果，浪费大量时间。

对数据存储的常见形式有数组和链表，数组便于查找，找一个元素的时间复杂度为O(1)，但数组不便于插入与删除。对于有n个元素的数组来说，要删除数组中第i个元素，为了节省空间，要腾出第i个位置的空间，由于数组间元素是连续存储的，所以需将第i+1个后面的所有元素均依次向前移动一个位置，然后删除第n个元素所在的空间，平均时间复杂度为O(n/2)。若采用链表方式存储，删除一个元素需O(1)时间即可。

在求正、负区域及简化决策表时，对于U/P(P⊂C)的划分中基数为1的子划分对象为可区分对象，无需参与下一步的划分过程，应将此对象加入正区域集，并在U中删除此对象。为了方便删除操作，可利用链表的结构特征，这样可有效加速求简化决策表的进度和减少搜索空间。算法1具体描述如下：

算法中涉及到的链表结点数据结构为：

structList{

data;

//数据在条件属性Ci上的取值

set;

//在Ci上取值data的数据集合

count;

//为集合set的数据个数

next;

//下一指针

}

输入：U,C,D

输出：简化决策表U′,POS,NEG

Step1初始化条件U′=U；POS=∅，NEG=∅；

Step2将决策表按条件属性C1进行划分，将样本在C1上取值相同的结点存储同一子划分中，并用链表List连接所有子划分。

Step3for(i= 2 toi< |C|){

Step3.1将List中的每个结点元素，按条件属性Ci划分，同类的样本编号放在同一结点的set中，若产生了新的加细划分，则相应产生新结点。

Step3.2连接链表，但要对子划分基数为1的划分加入POS中，且在List中删除此结点，实现剪枝。

Step4扫描链表List的每个结点，若某结点的set中数据有D值不同的，则选择set中第一个数据加入NEG，否则加入POS。

Step5POS并NEG得到简化决策表U′。

2.2算法1时间和空间复杂度分析

算法1的step1的时间复杂度为O(1)；Step2的时间复杂度为O(|U|)；Step3的时间复杂度为max(O((|C|-1)×(|U′|+|Ci|)))，其中Step3.1的时间复杂度O(|U′|)，由于U′在划分过程中，不断剪枝，所以|U′|≤|U|；Step3.2的时间复杂度为|Ci|；Step4的为O(|U′|)，因为最后List中链表的结点个数与简化决策表中的元素个数相同，扫描List每个结点所需时间为O(|U′|)；Step5的为O(1)，仅仅是将POS与NEG合并。

综上所得，时间复杂度为：

O(|U|)+ O(|U′|)+max(O((|C|-1)×(|U′|+|Ci|)))

由于|U′|≤|U|，且|U′|越来越小，故时间复杂度为O(|C‖U|)。

算法所需的空间，链表中共有的结点数实现就是样本按条件属性C划分得到的子划分个数，即O(|U/C|)，而每个结点4个成员，其中data、count和next共需空间O(4×|U/C|)，最终简化决策表空间O(|U/C‖C|)，所以空间复杂度为max(O(4×|U/C|),O(|U/C‖C|))。

3　启发式属性约简算法

3.1属性重要性度量

在进行数据约简时，通常先计算属性重要性，并以此为启发式信息选择最易区分的属性加入约简集。差别矩阵算法以对象间可区分的属性出现的频率作为依据，选择属性，此类算法直观、易理解，但需浪费大量的空间。为此，许多学者关注于改进差别矩阵[9-11]，试图减少差别矩阵元素。根据定义5可知，改进差别矩阵表中，正区域中所有按D划分属于不同子划分的数据进行比较，所有负区域中的每个数据与正区域的每个数据进行比较，但负区域中的所有数据相互间无需比较。与经典的差别矩阵相比，元素个数大大减少，但数据量还是比较庞大。经研究发现，可借助差别矩阵的直观性等优点，但无需建立差别矩阵方法。

(6)

(7)

性质2根据定义5的改进差别矩阵，对于某具体的简化决策表，其差别矩阵中元素个数一定，设为Mcount，则：

(8)

(9)

3.2启发式属性约简算法(算法2)

以不可区分对数DM(Ci)为启发式信息，设计属性约简算法(算法2)，具体如下：

structDList{

data；

//数据在条件属性Ci上的取值

List；

//在Ci上取值data的数据集合

count；

//为集合List中的数据个数

structDList*next；

//下一指针

}

输入：简化决策表U′，POS，NEG

输出：Core

Step1初始化C′=C，Core=∅，Count=0；

Step2while(Count++<|C|‖DList!=NULL) {foreachCiinC′ {

Step2.1求U′/Ci，且用DList链表存储每个子划分且按D进行划分，再按条件属性取不同值建立不同的List链表，并将List.count为0的结点删除；

Step2.2计算DM(Ci)；对DList.count数是0的结点剪枝。

Step2.3计算Min(DM(Ci))，C′=C=Ck，

Core=Core∪CK//Ck为取值最小的条件属性

}

}

Step3输出Core;

算法2的主要时间用在求属性重要度量方面。在求DM(Ci)时，主要扫描DList链表，DList的长度即为条件属性Ci划分所得的等价类数目|U′/Ci|，每个子划分再按决策属性D划分，最好情况下是一个条件属性就可将所有样本区分，时间复杂度为：

4　算法实例与实验分析

4.1算法实例

4.1.1求正、负区域及简化决策表过程

为进一步说明上述算法原理，下面用表1所示的数据介绍算法运行过程。

表1　决策表U

(1)POS=∅,NEG=∅；

(2)U/a分四类，构成的DList链表为:

(3) 在(2)基础上将各结点中的样本按条件属性b进行划分，并建立相应的链表得到：

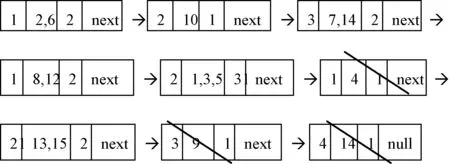
根据性质1可知，U中的10、4、9、11数据已经在链表中删除，同时加入了POS中，即POS={4,9,10,11}；

(4) 同理可得，继续按条件属性c、d划分得到：

POS={3,4,9,10,11}；

(5) 再将List中各结点的数据进行按D值划分，若有D值不同的，则将结点中的第一个数据样本加入到NEG中，否则加入到POS中，得到NEG={7,8}；POS={1,2,3,4,9,10,11,13}；U′的样本数据为{1,2,3,4,7,8,9,10,11,13}，具体简化决策表如表2所示。

表2　简化决策表U′

对于决策表U，采用文献[2]方法，每个条件属性需按关键字收集，包括属性共4个，需比较次数60，移动60次，得到U/C；最后再按决策属性D不同值收集，将C值相同而D值不同的所有子划分中第一个元素加入NEG，将C值相同且D值也相同的所有子划分第一个元素加入POS中，需比较15次，10次移动，总共需145次。若采用本文算法1，按属性a收集需15次比较，15次移动，再按属性b、c和d收集，分别需比较次数11、10和10，共46次比较，移动次数即为删除结点次，故需5次；此时，已有5个结点在POS中，再将U/C的5个子划分中元素进行比较，需5次比较5次移动得到POS和NEG，共56次比较和移动。

4.1.2属性约简过程

在上述简化决策表、正负区域基础上，建立DList链表得：

(1)DList(a):

DList(b):

子划分中带下划线的表明按D划分属于同类的。且最后一个结点被删除，因为其count为1。

DList(c):

DList(d):

Min(DM(a),DM(b),DM(c),DM(d))=8，所以选a或b属性加入Core。

(2) 设第一个选择的属性为b，则将DList(b)继续按属性a、c或d划分，得到：

DM(b,d)= 0+0=0，所以将d加入Core，此时所有样本已经区分，故约简集为Core={b,d}。同理可得，其他约简集有{a,b,c}。

4.2实验分析

求解简化决策表、正负区域是属性约简的关键环节，现将算法[1]与文献[2]算法进行比较。在AMDAthlonⅡX2 2402.78GHz,RAM1.5G，VC6.0环境下编程，采用UCI数据库中5个数据集为测试数据(D1:forestfires，D2:adult，D3:abalone，D4:mushroom，D5:poker_hand)，其中正区域记录数为Pi，负区域记录数为Ni，简化表记录数为Si)，执行过程中数据对比情况如表3所示。

表3　求U/C记录比较对照表

由表3可知，因选择的各数据集除D1有少量重复数据外，其他的测试数据均无重复数据，所以D2、D3、D4和D5数据简化前后无变化，且正区域的记录数等于简化决策表的样本数。虽然算法1与文献[2]求正区域的时间复杂度均为O(|C‖U|)，但算法1在求解时不断剔除已区分的样本。对于D2共15个属性，收集过程中第2个属性加入时已有107条数据可区分，第3个属性加入时有1675条数据区分，到第4个属性时已区分所有样本，其余属性就无需继续比较，所用时间相当于文献[2]的1/5。对于D4，效果不明显，将前10个属性逐趟收集，几乎没有可区分对象，直至第21个属性加入时有3764条数据已区分，导致求解效果不明显。由此可看出，在按条件属性不同值收集时，若某属性的加入能够区分的样本越多，采用算法1时，求正、负区域的速度越快，因为算法1对已区分的样本进行修剪，不参加下次的运算，减少搜索空间。

算法1的优势体现在求正区域上，在算法1的基础上，利用算法2对数据进行属性约简。算法2利用了差别矩阵算法的直观性、可理解性，但又没有差别矩阵算法所需的大量空间，所以算法2的优势又表现在空间的开销上。同样，用D1-D5的数据进行实验，得到算法2、文献[2]算法和文献[10]算法进行比较，如图1所示。

图1　各种算法时间性能对比

由图1可知，算法2比文献[2]算法略有提高，是因为在计算正区域时，能够有效剔除已区分的样本，且明显较文献[10]算法的约简时间效果好。从图中还可得，当|U|越大，且|C|越小时，文献[10]算法越显得不足。在|U‖C|较小时，算法2比文献[2]算法挖掘时间效果显示明确，但随着数据对象个数及条件属性个数增加，算法2的优势越来越不明显。在对样本D4、D5运算时，出现了挖掘时间呈下降趋势，而文献[10]一起呈上升趋势，是因为文献[10]的时间复杂度为O(|U|2|C|)，它随着|U|的增加，时间增速较文献[2]和算法2要快。

空间上，算法2较文献[10]也有优势，具体如表4所示。

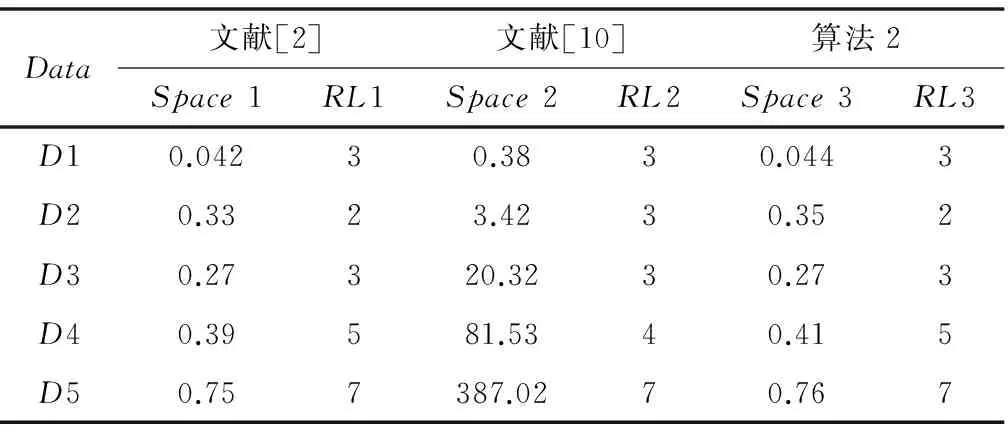
表4　多种算法空间占用比较

所示(Spacei为各算法所需空间，以MB为单位；RLi为各算法约简后的属性个数)。由表4可知，算法2在空间效果上比文献[10]也有很大改观。主要是因为文献[10]需大量空间存储二进制的信息矩阵。

5　结　语

属性约简过程中，正区域计算是很多属性约简算法必不可少的一步。通过对正、负区域的计算，可得到简化决策表，剔除冗余数据，加速属性约简进度。文献[2]的基数排序算法虽然效率较高，但未能在求简化决策表过程中进行剪枝，本文算法1可有效得到正、负域及简化决策表，且效率比文献[2]的算法略高。在求属性重要性度量时，引入DM(Ci)概念，充分利用差别矩阵算法的直观、易理解的优点，但又无需建立信息矩阵，大大减少存储空间。但目前的这些算法，只是针对静态数据库，而现实世界是不断变化的，下一步是如何适应动态数据库的属性约简。

[1]PawlakZ.Roughsets[J].InternationalJournalofComputerandInformationScience,1982,11(5):341-356.

[2] 徐章艳,刘作鹏.一个复杂度为的快速属性约简算法[J].计算机学报,2006,29(3):391-399.

[3] 王国胤,于洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.

[4] 杨明.一种基于改进差别矩阵的属性约简增量式更新算法[J].计算机学报,2007,30(5):815-822.

[5] 钱文彬,杨炳儒,徐章艳,等.基于差别矩阵的不一致决策表规则获取算法[J].计算机科学,2013,40(6):215-218.

[6] 梁宝华,汪世义,蔡敏.基于顺序表的启发式属性约简算法[J].计算机工程,2012,38(2):51-53.

[7] 张文修,米据生,吴伟志.不协调目标信息系统的知识约简[J].计算机学报,2003,26(1):12-18.

[8] 刘少辉,盛秋戬,吴斌,等.Rough集高效算法的研究[J].计算机学报,2003,26(5):524-529.

[9] 葛浩,李龙澍,杨传健.基于简化差别矩阵的增量式属性约简[J].四川大学学报:工程科学版,2013,45(1):116-124.

[10] 杨传健,葛浩,李龙澍.垂直划分二进制可分辨矩阵的属性约简[J].控制与决策,2013,28(4):563-569.

[11] 黄国顺,曾凡智,陈广义,等.基于区分能力的HU差别矩阵属性约简算法[J].小型微型计算机系统,2012,33(8):1800-1804.

[12] 葛浩,李龙澍,杨传健.基于差别集的启发式属性约简算法[J].小型微型计算机系统,2013,34(2):380-385.

HEURISTICSATTRIBUTEREDUCTIONALGORITHMBASEDONLISTSTRUCTURE

LiangBaohua

(Institute of Computer and Information Engineering,Chaohu University,Hefei 238000,Anhui,China)

Attributereductionisoneofmaincontentsinroughsettheoryresearch,andpositiveregioncalculationisthekeyofmostattributereductionalgorithms.Inordertoreducethetimeofpositiveregioncalculation,weproposedtheliststorage-basedpositiveregioncalculationmethod.Themethodstoresthedatawithsameattributevaluetosamenodedataoflist,duringthedatacollectingperiod,itcontinuouslydeletesthesubdivisionswith1astheircardinalnumber,byreducingthescaleofsampledataitdecreasescalculationtimeconsumptionandspeedsuptheattributereduction.Atthesametime,wegavethedefinitionofthenumberofpairsofindistinguishabledata,andusedittomeasureattributeimportance,anddesignedanefficientheuristicattributereductionalgorithm.Bytestingandcomparingtheperformancesofexamplesandexperimentswiththatofclassicalreductionalgorithm,theresultsprovedthatthismethodwaseffectiveandfeasibleintemporalandspatialeffects.

RoughsetAttributereductionListPositiveregionPairsnumberofindistinguishabledata

2014-10-15。国家自然科学基金项目(60573174)；安徽省高等学校省级自然科学研究项目(KJ2013Z231)。梁宝华，副教授，主研领域：粗糙集，数据挖掘。

TP181

ADOI:10.3969/j.issn.1000-386x.2016.03.061