一类变时滞忆阻器递归神经网络全局指数周期性
段飞腾 崔宝同
(江南大学物联网工程学院 江苏 无锡 214122)
一类变时滞忆阻器递归神经网络全局指数周期性
段飞腾崔宝同
(江南大学物联网工程学院江苏 无锡 214122)
忆阻器是近几年来提出的一种区别于电阻、电容、电感的一类非线性两端无源电子元件,而忆阻器递归神经网络由于系统参数的不同,系统表现出各种动态性能。针对一类变时滞忆阻器递归神经网络,研究全局指数周期性问题,考虑连接权值在切换状态下的对称和非对称的情况,通过构造两个Lyapunov函数、Halanay不等式和由Fillippov给出的右端不连续微分方程理论的研究方法,提出关于全局指数周期性的充分性条件。最后,实验结果验证了所提理论的可行性和有效性。
忆阻器周期解神经网络变时滞
0 引 言
忆阻器最初由LeonChua于1971年提出[1],2008年惠普实验室的研究人员终于发明了这种元件[2,3]。忆阻器是无源的两端电子元件,可以描述电荷和磁通量之间的非线性关系,它的阻值取决于施加在忆阻器上的电压的大小以及施加的电压的极性和时间。近年来,越来越多的学者和研究人员开始关注忆阻器的应用,比如利用忆阻器来构建忆阻器混沌电路[4],由于忆阻具有更加复杂的混沌路径,这种特性可以用于保密通信之中。除此之外,由于忆阻器具有存储的功能,研究人员通过忆阻来研发最新的非易失性存储器[5]。研究人员最感兴趣的是忆阻可以应用于人工神经网络,通过构成忆阻器神经网络来模拟人的大脑运行,从而为研究新一代模拟人脑运行的计算机奠定基础[6]。由忆阻器构成的神经突触组成的新一代的计算机具有低能耗、高度并行、以及事件驱动等特点[7],使得计算机的运行速度更加快。
递归神经网络在模式识别、信号处理和动态规划等领域中得到了广泛的应用[8-10],因此研究忆阻器递归神经网络显得尤其重要,许多学者开始研究忆阻器递归神经网络的动态性能。文献[11]首次研究了忆阻器递归神经网络的动态特性,通过构造合适的Lyapunov泛函和微分包含理论分析了忆阻器神经网络的全局一致渐近稳定性,提出了基于M-矩阵的充分性判据。文献[12]利用LaSalle不变集原理、Lyapunov泛函和M-矩阵方法研究了忆阻器递归神经网络耗散性和稳定性。文献[13]研究了一类基于常时滞的忆阻器神经网络的全局指数周期性和稳定性的问题。文献[14]研究了忆阻器神经网络的全局指数稳定性,其中连接权值在切换状态下是对称的。本文在文献[13,14]的基础上,考虑在实际应用中,由于切换时的状态变化连接权值不可能完全是对称的。因此本文探讨变时滞的情况下,利用Lyapunov函数、Halanay不等式和右端不连续微分方程理论,获得忆阻器神经网络全局指数周期性的充分性判据。
1 模型描述
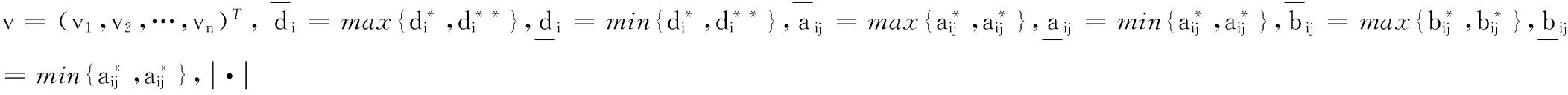
考虑如下的一类忆阻器递归神经网络[13,14]:
(1)
其中:

(2)

定义2[15]考虑如下右端不连续系统:
(3)
其中F(x):Rn→Rn是不连续的,其中集值映射定义如下:

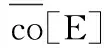

利用定义1和定义2,系统式(1)可以写成如下微分包含:
(4)

(5)

(6)
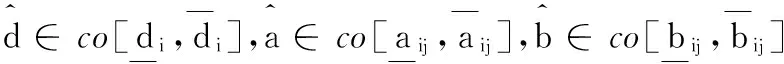
(7)
(8)
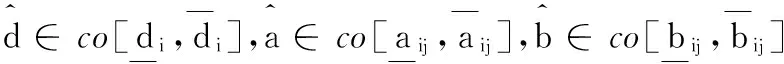
(9)
其中:
定义4如果系统式(1)任意初始点x(t)出发的轨迹满足:

其中μ和β是独立的恒定常数,那么称这个系统的平衡点x*处是全局指数稳定的。
引理1[16](Halanay不等式)常数a、b,且0 定理1对i,j=1,2,…,n,∀t>0,有: (10) 证明构造Lyapunov函数 (11) 计算V(z,t)沿式(9)轨迹的右上Dini导数,得: (12) 根据式(2),可知激活函数满足如下不等式: (13) 其中i=1,2,…,n,σi,ρi是非负的正整数。 由式(12)和式(13)得: 由式(10),可知a>b>0,利用引理1,存在ε>0使得: 由于zi=xi-x*,得: 因此,根据定义3,系统式(1)有唯一周期解,且周期解是全局指数稳定的。证毕。 定理2对i,j=1,2,…,n,∀t>0,有: (14) 证明同理构造另一个Lyapunov函数 (15) 计算V(z,t)沿式(9)的右上Dini导数,则: 根据式(13),可得: 由于zi=xi-x*,即: 根据定义3,系统式(1)有唯一的周期解,且周期解是全局指数稳定的。证毕。 本节将针对定理1和定理2中的变时滞忆阻神经网络的周期性条件分别进行验证。 例1考虑如下的忆阻器递归神经网络。 b11(x1)g1(x1(t-τ1(t)))+b12(x1)g2(x2(t-τ2(t)))+I1 b21(x1)g1(x1(t-τ1(t)))+b22(x2)g2(x2(t-τ2(t)))+I2 其中连接权矩阵是对称的,参数如下: 时滞τ1=1.8+0.5sin(t),τ2=2-0.8cos(t),外部的输入为I=(2sin(t),-2cos(t)),激活函数如下: 取σi=ρi=1,i=1,2.计算式(11)得: 根据定理1,系统具有唯一的周期解,且是全局指数稳定的,x1和x2各15个随机初始条件下的时间响应曲线和相平面曲线如图1和图2所示。 图1 系统状态x1(t)和x2(t)的状态响应曲线 图2 系统状态x1(t)和x2(t)的相平面曲线 例2考虑另一种连接权值不对称的情况,参数如下: 时滞τ1(t)=1.5+sin(t),τ2(t)=2-2cos(t),外部的输入为I=(10sin(t),-10cos(t)),激活函数如下: 计算式(14)可得: 从定理2可以推断,系统在权值不对称的情况下,系统依然具有唯一的周期解,且是全局指数稳定的,x1和x2各15个随机初始条件下的时间响应曲线和相平面曲线如图3和图4所示。 图3 系统状态x1(t)和x2(t)的状态响应曲线 图4 系统状态x1(t)和x2(t)的相平面曲线 本文提出的两个定理不同于文献[13,14]。与文献[13]相比较,本文考虑了时滞是变化的情况,而文献[13]仅仅考虑的时滞是常数。而文献[14]中仅仅考虑了连接权值是对称的,而本文中不仅仅考虑连接权值是对称的情况,而且考虑了连接权值在不对称情况下的周期性,与文献[14]相比,本文的结果考虑得更加全面,应用的范围更广。 本文主要针对一类变时滞忆阻器神经网络,研究了全局指数周期性问题。在文献[13,14]的基础之上,继续考虑系统的时滞是变化的情况和连接权矩阵的对称和非对称的,在Filippov右端不连续微分方程理论框架下,将不连续系统转化为微分包含来研究,通过构造两个李雅普诺夫函数以及不等式的方法,得到了关于全局指数周期性的两个判据,并且本文考虑的权值和时滞的变化范围更广。通过两个仿真的例子可知,说明本文所得到的定理是可行且有效的。 [1]ChuaLO.Memristor-themissingcircuitelement[J].IEEETransactiononCircuitTheory,1971,18(5):507-519. [2]StrukovDB,SniderGS,StewartDR,etal.Themissingmemristorfound[J].Nature,2008,453(7191):80-83. [3]WilliamsR.Howwefoundthemissingmemristor[J].Spectrum,IEEE,2008,45(12):28-35. [4] 包伯成,史国栋,许健平,等.含两个忆阻器混沌电路的动力学分析[J].中国科学:技术科学,2011,41(2):1135-1142. [5] 段书凯,胡小方,王丽丹,等.忆阻器阻变随机存取存储器及其在信息存储中的应用[J].中国科学:技术科学,2012,42(6):754-769. [6]BayatFM,ShourakiSB,AfrakotiIE.Bottleneckofusingasinglememristivedevicesasasynapse[J].Neurocomputing,2013,115:166-168. [7]MorabitoFC,AndreouAG,ChiccaE.Neuromorphicengineering:fromneuralsystemstobrain-likeengineeredsystems[J].NeuralNetworks,2013,45(9):1-3. [8]CaoJ,YuanK,LiHX.Globalasymptoticstabilityofrecurrentneuralnetworkswithmultiplediscretedelaysanddistributeddelays[J].IEEETransactionsonNeuralNetworks,2006,17(6):1646-1651. [9]CaoJ,WangJ.Globalasymptoticandrobuststabilityofrecurrentneuralnetworkswithtimedelays[J].IEEETransactionsonCircuitsandSystemsI:RegularPapers,2005,52(2):417-426. [10]LiuQ,WangJ.Aone-layerrecurrentneuralnetworkwithadiscontinuoushard-limitingactivationfunctionforquadraticprogramming[J].IEEETransactionsonNeuralNetworks,2008,19(4):558-570. [11]HuJ,WangJ.Globaluniformasymptoticstabilityofmemristor-basedrecurrentneuralnetworkswithtimedelays[C]//InternationalJointConferenceonNeuralNetworks,Barcelona,Spain,2010:1-8. [12]ZhenyuanGuo,JunWang,ZhengYan.Globalexponentialdissipativityandstabilizationofmemristor-basedrecurrentneuralnetworkswithtime-varyingdelays[J].NeuralNetworks,2013,48(12):158-172. [13]GuodongZhang,YiShen,QuanYin,etal.Globalexponentialperiodicityandstabilityofaclassofmemristor-basedrecurrentneuralnetworkswithmultipledelays[J].InformationSciences,2013,232(5):386-396. [14]GuodongZhang,YiShen,JunweiSun.Globalexponentialstabilityofaclassofmemristor-basedrecurrentneuralnetworkswithtime-varyingdelays[J].Neurocomputing,2012,97(11):149-154. [15]BacciottiA,RosierL.LiapunovFunctionsandStabilityinControlTheory[M].2nded.NewYork:SpringerBerlinHeidelberg,2006. [16]DongmingZhou,JindeCao.Globallyexponentialstabilityconditionsforcellularneuralnetworkswithtime-varyingdelays[J].AppliedMathematicsandComputation,2002,131(2):487-496. GLOBALEXPONENTIALPERIODICITYOFACLASSOFMEMRISTOR-BASEDRECURRENTNEURALNETWORKSWITHTIME-VARYINGDELAYS DuanFeitengCuiBaotong (School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,Jiangsu,China) Memristorisanonlineartwo-terminalpassiveelectroniccomponent,whichisproposedinrecentyearsandisdifferentfromtheresistor,capacitorandinductor.Thememristor-basedrecurrentneuralnetworks,withdifferentsystemparameters,showallkindsofdynamicperformances.Weinvestigatedglobalexponentialperiodicityprobleminregardtoaclassofmemristor-basedrecurrentneuralnetworkswithtime-varyingdelays,andconsideredthesymmetryandasymmetrysituationsofconnectionweightsinswitchingstate.ViathestudyingapproachofconstructingtwoproperLyapunovfunctions,theHalanayinequalityandthetheoryofdifferentialequationswithdiscontinuousright-handsidesintroducedbyFillippov,wepresentedthesufficiencyconditionconcerningtheglobalexponentialperiodicity.Finally,experimentalresultsverifiedthefeasibilityandeffectivenessoftheproposedtheory. MemristorPeriodicsolutionNeuralnetworksTime-varyingdelays 2014-09-27。段飞腾,硕士,主研领域:神经网络。崔宝同,教授。 TP273 ADOI:10.3969/j.issn.1000-386x.2016.03.041
2 忆阻器神经网络全局指数周期性

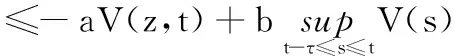
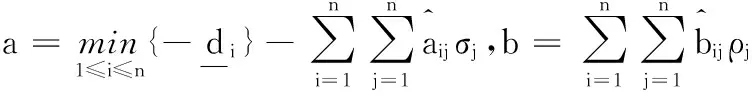
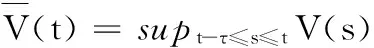
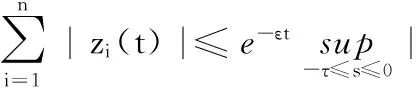



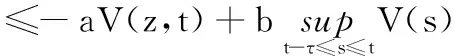
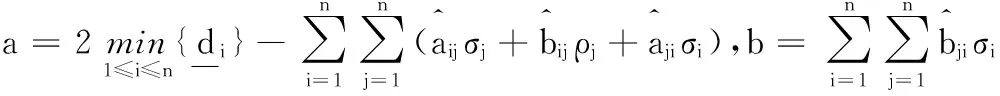
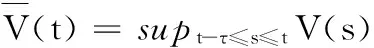


3 仿真示例




4 结 语

