一种自适应的弱选择压缩采样匹配追踪算法

陈秋芳，祖兴水，李宝清（1.中国科学院 上海微系统与信息技术研究所，无线传感网与通信重点实验室，上海　201800；2.中国科学院 上海微系统与信息技术研究所 微系统技术国防科技重点实验室，上海　201800；3.中国科学院大学 北京　100049）

一种自适应的弱选择压缩采样匹配追踪算法

陈秋芳1，3，祖兴水1，3，李宝清1，2
（1.中国科学院 上海微系统与信息技术研究所，无线传感网与通信重点实验室，上海201800；2.中国科学院 上海微系统与信息技术研究所 微系统技术国防科技重点实验室，上海201800；3.中国科学院大学 北京100049）

针对实际中未知稀疏度信号的重建问题，提出了一种自适应的弱选择压缩采样匹配追踪算法。该算法将自适应思想、弱选择思想与CoSaMP算法相结合，在预选阶段后利用限制性弱选择策略对候选集进行二次筛选，通过双迭代阈值自适应地调整最终支撑集的原子数，并结合若干可靠性验证条件，保证算法的正确有效进行。MATLAB仿真结果表明，在相同的实验条件下，本算法可以有效地重建稀疏信号，同时具有较低的运算量，整体性能较优。

压缩感知；重建算法；自适应；弱选择；压缩采样

随着信息技术的飞速发展，人们对信息的需求量与日剧增。然而，传统的遵循Nyqusit采样定理的信号采样方式造成了资源的严重浪费。2006年，Candes、Tao等人提出了压缩感知（Compressed Sensing/Sampling，CS）理论［1-4］，尝试将信号采样和数据压缩合二为一。它突破了传统奈奎斯特采样定理的限制，降低了信号测量的成本和对硬件设施的压力。

压缩感知的核心问题是采用重建算法从低维的测量样本中高概率地恢复出原始的高维数据。已经提出的信号重建算法包括基追踪算法（Basis Pursuit，BP）［5］和匹配追踪算法（Matching Pursuit，MP）［6］等，而 MP及其后续改进算法因重建复杂度较低得到了广泛的应用。正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法［7］每次迭代只得到支撑集的一个原子，效率较低。Needell等人提出了正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit，ROMP）算法［8］和压缩采样匹配追踪（Compressive Sampling Matching Pursuit，CoSaMP）算法［9］。ROMP利用正则化过程实现原子的快速、有效选择，重建效率较高。CoSaMP引入了回溯的思想，重建复杂度较低。以上各算法虽然重构速度较快，但都需要信号稀疏度K作为输入条件，而在实际中K往往是未知的，若K估计不合适会造成重构结果不稳定。

分段正交匹配追踪（Stagewise Orthogonal Matching Pursuit，StOMP）算法［10］、分段弱正交匹配追踪（Stagewise Weak Matching Pursuit，SWOMP）算法［11］和稀疏度自适应匹配追踪（Sparsity Adaptive Matching Pursuit，SAMP）算法［12］都摆脱了对稀疏度的依赖。

1　稀疏表示和压缩感知

设x是大小为N×1的原始信号。现实中我们感兴趣的信号一般本身并不稀疏，但在某个变换域是ψ稀疏的，记为稀疏表示模型x=ψθ。其中，ψ是大小为N×N的稀疏矩阵，θ（N× 1）为K稀疏的展开系数向量，即θ只有K个非零项。

用一个与稀疏矩阵ψ不相关的M×N维观测矩阵Φ实现压缩观测：y=Φx。其中，y是大小为M×1的观测向量，一般有K＆lt;＆lt;M＆lt;＆lt;N。此时，y=Φψθ，令传感矩阵AM×N=Φψ，A的列向量｛aj，j=1，2，…，N｝作为原子，则有：y=Aθ。文中要解决的问题可以用以下最小l0范数问题描述：

通过式（1）得到原始信号稀疏表示的系数估计θˆ后，根据式ˆ=ψˆ就可以重构出x。然而，利用l0范数求稀疏解属于NPHard问题，计算复杂度高。l1范数求解属于凸优化的线性规划问题，因此经常考虑将l0范数等价为l1范数求解。文献［13］表明：当传感矩阵满足约束等距特性（Restricted Isometry Property，RIP）条件时，就能通过求解范数最小化问题精确重构稀疏信号x。研究发现［14］，当M≥cKlog（N/K）（c是一个很小的常数）时，若以高斯随机矩阵作为测量矩阵，传感矩阵A以极大概率满足RIP性质。

2　自适应的弱选择压缩采样匹配追踪算法

2.1正交匹配追踪及其改进算法

在正交匹配追踪中，残差总是与已经选择过的原子正交的，意味着已经选择过的原子不会被选择两次，结果会在有限的几步收敛。但是，OMP算法每次迭代只选择与残差最相关的一列，重构效率非常低，因此研究人员开始提出每次迭代可选择多个原子的改进算法。

CoSaMP算法每次迭代时先选择2K个原子作为初始候选集，然后合并当前支撑集中的K个原子组成最终候选集，之后利用回溯思想按照一定规则逐步剔除候选集中的部分原子，最终保留最匹配的K个原子用于信号重构。从以上过程看出，必须适当估计信号稀疏度K才能进一步精确重建信号。此外，固定数目的原子选择方式也未能充分体现不同迭代残差与观测矩阵中各原子相关性的差异，在筛选中必定会造成预选浪费，影响算法的重构精度。

SWOMP算法引入了原子的弱选择标准，门限设置为：Th=α·max（u），α是门限参数。将相关系数不小于Th的原子的索引值并入候选集中，则完成了一次原子的弱选择。弱选择标准使算法重构效果不受稀疏度的影响，并能更灵活地挑选原子，提升重构效果和稳定性。

SAMP算法也不需要知道信号的稀疏度K。该算法将同一个迭代过程分成多个阶段，通过转换阶段不断增加支撑集的大小从而逐渐逼近信号实际稀疏度K，直至满足迭代终止条件。该算法具有较高的重构概率，缺点是分阶段迭代造成了重构时间较长。算法需要选取合适的初始步长，本文算法和SAMP算法相同，采用式（2）来设定初始步长［15］：

综上所述，采用回溯思想的CoSaMP算法虽然重构效率高，但需要以稀疏度作为先验信息，原子选取方式不灵活，重构精度不太高。据此，引入SWOMP算法的弱选择原则和SAMP算法的自适应思想可以克服CoSaMP算法的以上缺点。改进算法不需要信号的稀疏度先验信息，可以根据弱选择方法和自适应过程自动调整所选原子数来重建未知稀疏度的信号。

2.2自适应弱选择压缩采样匹配追踪算法

算法具体步骤如下：

输入：观测向量y，传感矩阵A，门限参数α

初始化：迭代次数i=1，残差r0=y，步长s=M/［1lb（N）］，阶段stage=1，则初始支撑集大小L=s，算法的最大迭代次数取为测量数M，支撑集Λ0为空集。

现迭代执行如下步骤：

1）利用u=|AT·rt-1|计算相关系数u，将u中2L个最大值对应A的索引值构成集合J0；

2）选择集合J0中索引值对应原子相关系数大于门限Th= α·max（u）的值，将这些值对应A的索引值构成集合J；

3）合并索引集合，令C=Λi-1∪J，Ai=Ai-1∪aj（for all j∈J）；

4）求y=Aiθi的最小二乘解Ai）-1ATiy。从θˆi中选出绝对值最大的L项记为θˆiL，对应A中的列记为AiL，对应A的索引值记为F；

5）更新残差rnew=y-AiL（ATiLAiL）-1ATiLy；

6）如果残差rnew＆lt;ε1则令Λi=F，并停止迭代进入步骤7）；如果‖rnew-ri-1‖≤ε2，更新阶段stage=stage+1，更新步长L=s· stage，返回步骤1）；若前面两个条件都不满足，则令Λi=F，ri= rnew，i=i+1，如果i＞M则停止迭代进入步骤7），否则转至步骤1）继续迭代；

对于以上算法步骤，有两点需要详细说明：

①在步骤2）侯选集的二次筛选中，SWOMP中门限参数α的取值范围一般为0＆lt;α≤1，本文算法采用限制性弱选择策略，只取的较优值，选择过程见下文MATLAB仿真实验。

②步骤6）中，ε1是控制迭代次数的阈值，ε2是控制阶段转换的阈值，双阈值可以保证算法具有较好的重建精度。当残差能量小于ε1时停止迭代。根据经验，ε1选择为1e-6。当时，表示没有新的原子被加入支撑集，说明L需要更新以满足重建要求。

为了使算法能够正确有效地进行，文中还加入了两个可靠性验证条件，简述如下：

①步骤4）中求最小二乘解时，必须满足矩阵Ai的行数大于列数，即是列满秩矩阵，否则将不可逆。因此，当行数小于列数时，提前结束循环，并给赋值为0。

②因为采用了弱选择过程对原子进行二次筛选，因此索引集C的大小可能小于L，此时步骤4）中直接令F=C即可。

3　MATLAB仿真实验结果对比及分析

为了验证本文算法的重构性能，通过MATALB处理平台进行性能测试，并与已有的OMP、CoSaMP、SWOMP和SAMP算法进行对比分析，处理器是Intel Core i5-4300U。实验中选用一维高斯随机矩阵作为测量矩阵，单位矩阵作为稀疏矩阵，原始信号长度。

3.1弱选择门限参数的限定

α的范围是0.1～1，每隔0.1取一个值。K的范围是5～40，每隔5取一个值。现绘制门限参数α取10个测量值时，测量数M与重构成功概率的关系曲线。绘制结果共7幅图，当K= 25时，测量数M与重构成功概率关系曲线如图1所示。

图1　α取不同值时信号重构成功概率与测量数M的关系

从图1可以看出，选择不同的参量重构效果存在一定的差异。总体上讲取0.4，0.5，0.6时效果较好。观察K取其他值时另外6幅图，可得到相同的结论。因此，本文算法的输入参数α的取值范围限制为0.4，0.5，0.6。后文没有特别说明时，α默认取为0.5。

3.2本文算法单次重构效果

取测量数M=128，稀疏度K=25，某次运行结果如图2所示。

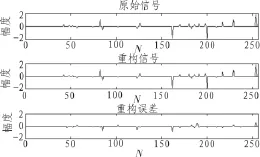
图2　单次重构时本文算法的原始信号和重构信号比较

可以看出，本文算法对一维原始信号的重建效果很好，重构误差较小，在量级。

3.3不同算法重构性能对比和分析

图3给出了当稀疏度K=25时，测量数M与重构成功概率关系曲线。信号重构成功是指重构信号与原始信号的误差的绝对值小于某一阈值，在此取为1e-6。由图可以看出，信号重构成功概率随着测量次数M的增大而增大。当M较小时5种算法重建效果都比较差，但是随着压缩比的不断增加，本文算法的重构成功概率相对OMP、CoSaMP和SWOMP算法提高很多，并略高于SAMP算法，本文算法和SAMP算法能稳定重建信号所需的采样点数均较少。该图说明了在稀疏度相同时，本文算法具有较优的重构概率。

图3　稀疏度K=25时重构成功概率与测量数M的关系

图4给出了当测量数M=128时，稀疏度K与重构成功概率关系曲线。由图可以看出，信号重构成功概率随着稀疏度K的增大而减小，并且本文算法远优于OMP、CoSaMP和SWOMP算法，在稀疏度较大时依然能精确重构信号，具有最佳的重构概率，而SAMP算法重构概率整体略低于本文算法。该图说明了在压缩比相同时，本文算法具有较优的重构概率。

图4　测量数M=128时重构成功概率与稀疏度K的关系

图5给出了当测量数M=128时，稀疏度K与运行时间关系曲线。本文算法因为迭代次数增加而导致运算时间整体略超过CoSaMP和SWOMP算法，但远小于OMP和SAMP算法。该图说明了在压缩比相同时本文算法具有比较少的重构时间。

通过以上各实验结果，综合各种算法的优劣势对比结果可知，本文所提出的算法是一种具有精确重构性能且重建复杂度较低的算法。

图5　测量数M=128时平均运行时间关系与稀疏度K的关系

4　结　论

本文在分析和总结已有压缩感知重建算法特点的基础上，提出了一种自适应的弱选择压缩采样匹配追踪算法。该算法同时结合了SAMP算法重构概率高、SWOMP算法不需要输入稀疏度且原子选择方式灵活和CoSaMP算法重构复杂度低的优点。仿真结果表明，在相同条件下，本文算法的重构效果优于OMP、SWOMP和CoSaMP算法，略优于SAMP算法，且其重构复杂度较低，且远低于SAMP算法，说明本文算法是一种重建质量较优的压缩感知重建算法，具有较高的实用性。

［1］Candes E J，Tao T.Decoding by linear programming［J］.IEEE Transactions on Information Theory，2005，51（12）:4203-4215.

［2］Donoho D L.Compressed sensing［J］.IEEE Transactions on Information Theory，2006，52（4）:1289-1306.

［3］Candes E J，Tao T.Near-optimal signal recovery from random projections:universal encoding strategies［J］.IEEE Transactions on Information Theory，2006，52（12）:5406-5425.

［4］Candes E J，Romberg J，Tao T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）:489-509.

［5］Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit［J］.SIAM journal on Scientific Computing，1998，20（1）:33-61.

［6］Mallat S G，Zhang Z.Matching pursuits with time-frequency dictionaries［J］.IEEE Transactions on Signal Processing，1993，41（12）:3397-3415.

［7］Tropp J，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2007，53（12）:4655-4666.

［8］Needell D，Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit［J］.IEEE Journal of Selected Topics in Signal Processing，2010，4（2）:310-316.

［9］Needell D，Tropp J A.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples［J］.Applied and Computational Harmonic Analysis，2009，26（3）:301-321.

［10］Donoho D L，Tsaig Y，Drori I，et al.Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit［J］.IEEE Transactions on Information Theory，2012，58（2）:1094-1121.

［11］Blumensath T，Davies M E.Stagewise weak gradient pursuits ［J］.IEEE Transactions on Signal Processing，2009，57（11）: 4333-4346.

［12］Do T T，Gan L，Nguyen N，et al.Sparsity adaptive matching pursuit algorithm for practical compressed sensing［C］.2008 42ndAsilomarConferenceonSignals，Systemsand Computers，2008:581-587.

［13］Candes E J，Romberg J，Tao T.Robust uncertainty principles:Exact signal reconstruction from highly incomplete frequency information［J］.IEEE Transactions on Information Theory，2006，52（2）:489-509.

［14］Baraniuk R G.Compressive sensing［J］.IEEE signal processing magazine，2007，24（4）:118-121.

［15］高睿，赵瑞珍，胡绍海.基于压缩感知的变步长自适应匹配追踪重建算法［J］.光学学报，2010（6）:1639-1644.

【相关参考文献链接】

高键，张凯.基于云模型自适应算法的船舶航向控制［J］.2015，23 （10）:36-38.

朱艳，李建祯.基于自适应混沌粒子群算法的推力分配研究［J］. 2015，23（13）:75-78.

席东河，王林生，刘明黎，等.基于ATT7037AU的新型自适应智能用电控制终端设计［J］.2015，23（13）:82-85.

熊淦辉，黎沛坚，徐俊林，等.基于自适应匹配模型的停电管理系统设计与应用［J］.2015，23（16）:160-163.

王坤.互动多媒体图片自适应大小的研究与实现［J］.2015，23 （18）:69-71.

荆海霞，李洪义.基于主动时间反转的水下目标自适应聚焦研究［J］.2015，23（24）:179-182.

朱宗明，姜占才.小波递归最小二乘语音自适应增强［J］.2016，24（1）:69-72.

黄业文，杨荣领，邝神芬.基于贝叶斯决策的自适应p-持续CSMA协议［J］.2016，24（1）:73-76.

郭璐，黄鹤，杜凯，黄莺，等.DSP环境下新的变步长LMS自适应滤波算法［J］.2016，24（1）:135-137.

刘桂辛.改进的自适应卡尔曼滤波算法［J］.2016，24（2）:48-51.

郑建英，于占东.磁悬浮球系统的自适应反演滑模控制［J］. 2016，24（2）:76-78.

樊润洁.基于全局鲁棒滑模PMSM自适应模糊控制［J］.2016，24 （4）:84-86.

An adaptive weak-selection compressive sampling pursuit algorithm

CHEN Qiu-fang1，3，ZU Xing-shui1，3，LI Bao-qing1，2
（1.Key Laboratory of Wireless Sensor Networks and Communication，Shanghai Institute of Microsystem and Information Technology，CAS，Shanghai 201800，China；2.Key Laboratory of National Defense for Science and Technology on Microsystem，Shanghai Institute of Microsystem and Information Technology，CAS，Shanghai 201800，China 3.University of Chinese Academy of Sciences，Beijing 100049，China）

This paper proposed an adaptive weak-selection compressive sampling pursuit algorithm to reconstruct signals with unknown sparsity in practice.The algorithm combines adaptive idea and weak-selection idea with the CoSaMP algorithm.It adopts limited weak-selection strategy to realize the second selecting of the atoms in the candidate set after the pre-selection stage，and then adaptively adjust the number of atoms in the final support set through double-threshold.We also incorporate some reliability demonstration conditions to the algorithm to ensure the correctness and effectiveness.The simulation results on MATLAB show that our algorithm can get better reconstruction performances and can run fast under the same conditions，which has a better overall performance.

compressed sensing；reconstruction algorithms；adaptive；weak selection；compressive sampling

TN914.3

A

1674－6236（2016）11-0150-04

2015-12-31稿件编号：201512325

微系统技术国防科技重点实验室基金项目（9140C18010214XXXX）

陈秋芳（1990—），女，河南商丘人，硕士。研究方向：压缩感知和稀疏表示。