基于蚁群算法和Petri网的井下有轨运输调度优化

朱启航　周　杰　张文举

(武汉理工大学资源与环境学院)



基于蚁群算法和Petri网的井下有轨运输调度优化

朱启航周杰张文举

(武汉理工大学资源与环境学院)

为解决地下矿山有轨运输调度问题，将Petri网理论引入矿山井下有轨运输调度优化中，结合蚁群算法思想，建立基于蚁群算法的赋时Petri网模型，并将蚁群系统算法机制改进后用于Petri网模型的分析，在模型中加入了根据地下矿山有轨运输系统改进过的时间戳状态类，使模型能够更好地处理运行过程中信息素、启发式因子等，优化参数与时间、状态之间的关系，建立了优化计算的详细步骤，简化了计算。并用计算实例验证了优化方法的有效性。

调度优化井下运输赋时Petri网蚁群优化

在地下矿山中，矿石运输是采矿工程中非常重要的一环。目前，有轨运输仍然是主要运输方式。有轨运输调度的合理与否，不仅关系到矿山的经济效益，还涉及到矿山的安全问题。不合理的运输调度不仅浪费矿山资源，还很可能发生相撞等安全事故。然而，传统矿山较少关注井下运输调度优化，特别是有轨运输的调度优化，相关研究也不多。

根据矿山地下有轨运输的特点，采用基于蚁群优化的赋时Petri网对运输调度系统建模，用改进的蚁群算法进行优化。引入时间戳状态类思想[1]，将蚁群算法中的蚂蚁信息素引入到Petri网的变迁中，设置信息素与变迁输出库所的时延相关联，将蚁群算法的寻优规则融合进Petri网的进化规则中。运算时设置蚂蚁令牌，根据进化规则运行多次，便可逐步找到最优路径，即可确定最优调度方案。

1　基于蚁群算法优化的时间Petri网模型

在Petri网中，将系统抽象为活动(事件)、状态及其之间的关系，组成三元结构。一般用库所P(Place)表示状态，用迁移T(Transition)表示活动[2]。库所能够决定迁移是否发生，而迁移可以改变库所状态，他们之间的相互依赖关系用输入函数和输出函数来表示。

结合蚁群算法，根据矿山地下有轨运输特点，建立赋时Petri模型：

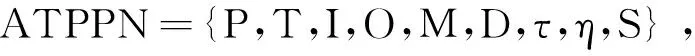
(1)

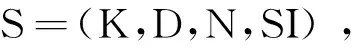
(2)

式中，P={p1， p2，…，pn}为有限位置的集合，n为库所数量，n>0；T={t1，t2，…，tm}为有限迁移的集合，m为变迁数量，m>0(P与T需满足以下关系：P∩T=φ，P∪T≠φ，保证位置与变迁是两种不同类型的元素，同时网中至少有一个元素)；I：P×T→N是输入函数，定义从库所P到变迁T有向弧的权的集合，这里N={0，1，…}为非负整数集；O：T×P→N是输出函数，定义从变迁T到库所P有向弧的权的集合；M为Petri网的令牌(token)，为一列向量，其中第i个元素表示第i个库所中的令牌数目，采用赋时库所Petri网；D={d1，d2，…,dn}为所有操作库所的时延集，其中di表示库所Pi的时延大小;S为时间戳状态类[3]；K为前n项中所有操作库所中令牌数不为零的库所号，即电机车所在位置，在本调度系统中n为电机车数量，K为n项的数列，K={Pi，Pj，…,Pn};N为采场所需矿车数量资源库所中的令牌数量，为每个采场需要的矿车数量；SI为时间戳状态类的时间戳，为全局时间区间，正表示网从最初状态S0运行到Si的全局时间，只有当变迁发生时，时间戳状态类才会发生改变，每次变迁发生后，如果状态类在状态类库中不存在，则将当前状态类放入状态类库，状态类库中储存着所有出现过的状态类；τ为变迁的信息素映射函数，τ(t)为变迁上的信息素数量，初始时，计算所有库所延时之和，取其倒数，并平均分配到每一个变迁上，作为每个变迁初始时的信息素值τ0(ti)[4]。

初始时所有变迁上的信息素值相同，计算式如下：

(3)

由于调度系统与系统状态相关，同一个变迁可能在不同的状态下发生，变迁每次发生的重要性不同，变迁中的信息素值也应该不同，将信息素值与系统状态相关联，建立与状态类相关的信息素矩阵τij(i为变迁编号，j为状态类编号)，τij中包含了所有状态所有变迁的信息素的值。为简化计算程序，用同一个状态信息τi0表示每个变迁所有未出现过的状态信息素值。

η为变迁的启发式因子映射函数，η(t)为变迁上的启发式因子，计算时将变迁之后库所的延时时间的倒数作为变迁初始的启发式因子，由于部分库所的延时为零，为了避免分母部分为零，在分母部分加1[5]，计算式如下：

(4)

式中,di为变迁之后操作库所中的延时时间。

与信息素相同，启发式因子也与状态类相关，同样建立启发式因子值矩阵ηij。

2　进化规则

2.1变迁发生的条件

变迁发生必须同时满足两个条件：变迁必须是使能的，输入库所中的令牌必须是有效的。

I(tj)表示输入函数中到变迁ti的所有权值，如果I(t)≤M，那么变迁ti是使能的。判断变迁能否发生还需判断输入操作库所中的令牌是否有效。变迁发生时的状态类时间戳为SI(i)，判断SI(i)与令牌变为有效的时间集D中D(j)的大小，如果SI(i)≥D(j)，那么状态类K中第j个库所中令牌为有效的。由于状态集K中记有当前电机车所在位置信息，即库所编号，所有可能使能的变迁必定以有电机车在的库所为输入库所，所以判断时，只需判断有机车在的库所为输入库所的变迁是否使能，即只需判断当前状态类中K中库所对应的变迁即可，大大减少了优化时的计算量。记状态为k时所有可以发生的变迁记为Fr(k)。

2.2激发变迁的选择

将当前发生的变迁视作蚁群算法中蚂蚁当前所在的城市，下一个激发的变迁即为蚂蚁将要前往的城市，变迁是否发生，参照蚁群算法中选择下一个城市的方法确定。引入在区间[0，1]均匀分布的随机变量q，q0是一个伪随机比例参数(0≤q0≤1)。通过比较q与q0的大小，确定选择变迁的方式。

当q≤q0时，按照先验知识选择路径，用以下公式选择激发的变迁：

(5)

式中，τk(t)为变迁t在状态k时的信息素值；ηk(t)为变迁t在状态k时的启发式信息值。在可以发生的变迁中选择括号中值最大的变迁tj激发。

当q≥q0时，使用赌轮法选择激发的变迁，变迁tj激发的概率为：

(6)

以上两个公式中，为调整路径长度与信息素之间的相对重要程度参数，这种选择规则称为伪随机比例规则，倾向于选择路径较短且信息素浓度较大的路径前行。利用先验知识与探索新的路径之间的相对重要程度由参数q0的大小来决定。q0较大时，倾向于使用先验知识选择，选择已经走过的路径中最好的，这样能更快收敛，但容易陷入局部最优解中；q0较小时，进行概率式搜索，更容易探索新的路径。

2.3变迁的激发

在确定要激发的变迁之后，对变迁实施激发操作，变迁的激发将导致状态类的改变。变迁发生时，首先进行库所令牌的更新，减去对应输入资源库所中的令牌，同时在输出库所中放入令牌：∀p∈·t：m′(p)= m(p)-I(p，t)；∀p∈t·：m′(p)=m(p)+O(t，p)。接着更新时间戳状态类，当激发状态类中第i个库所对应的变迁时，将时间戳状态类中的K(i)中的库所号由激发变迁的输入库所改为输出库所，并记录当前时间戳加上输出库所时延值的大小到D(i)中。

2.4信息素更新

在变迁发生之后，马上对此刻该变迁的信息素进行更新，称为局部更新。通过局部更新，增加有蚂蚁经过的变迁的信息素值。如果在状态k时，变迁ti激发，那么该状态下局部信息素利用以下公式进行更新：

(7)

当一次迭代中所有蚂蚁都完成了运行，在所有路径中选取从初始标识到最终标识的最优路径，对于最优路径上的所有变迁应用下式对信息素进行更新：

(8)

式中，ρ为从0到1的参数，代表信息素挥发的速度;Lop为到目前为止找到的最优路径运行的总时间。

其他状态下按照不在全局最优路径上的公式进行更新。通过全局更新，最优路径上的变迁信息素增多，在后面的迭代中，最优路径被选择的几率变大。而其他路径的信息素挥发则将变淡。

3　优化计算步骤

(1)初始化参数。设置循环次数，初始标识下每个库所中的令牌数量为m，变迁输入函数I(P，T)，变迁输出函数O(P，T)，操作库所的时延值大小D，每个变迁上的初始信息素值τk(t)和启发式因子ηk(t)，建立数列N用于记录变迁发生时的状态类编号。建立状态类库，状态类库中开始时只储存初始状态类。

(2)设置初始时间戳为当前状态类。

(3)寻找使能的变迁。根据变迁发生的条件，找出所有使能变迁，若没有转至第(7)步。

(4)按照变迁的选择规则选择出激发的变迁。

(5)激发变迁。按照变迁的激发规则激发变迁，如果当前状态类不在状态类库中，将当前状态类放入状态类库，之后转至第(3)步。

(6)判断是否达到目标标识，达到目标标识转第(8)步，否则运行第(7)步。

(7)增加全局时间(本例中为10s)，即增加当前状态类时间戳。之后判断时间戳是否到达最大时间，没有到达转至第(3)步，达到转至第(8)步。

(8)记当前状态类时间戳为此次循环运行时间，第一次循环时，直接将此次循环时间记为最优时间，此次循环中变迁激发的状态类编号记为最优顺序。后面的循环与此前的最优时间相比，若此次循环时间小于最优时间，记此次循环时间为最优时间，并将此次循环变迁激发的状态类编号记为最优顺序；若此次循环时间大于当前最优时间，最优时间与最优顺序不变。

(9)全局信息素更新。

(10)如果当前循环次数小于规定的循环次数，循环次数加1，转至第(2)步；如果当前循环次数达到规定的循环次数，输出当前最优时间，最优状态类顺序。

通过以上过程的多次循环，便可找出最优或者较优的运行路径，输出作为优化结果。

4　计算实例

图1为一巷道运输简图[6]。应用蚁群优化的赋时库所Petri网对这一运输系统进行建模，并且进行优化，再用其他优化方法对比，以验证效果。

图1　巷道运输简图

图1中CH为井底车场，CH1，CH2，CH3分别为1#、2#、3#采场车场，电机车在井底车场与采场车场之间运行，将采场的矿石运至井底车场。记前往1#采场运输的电机车为电机车(Ⅰ)，前往2#采场的电机车为电机车(Ⅱ)，前往3#采场的电机车为电机车(Ⅲ)。采场车场只能同时容纳一列电机车。前往3#采场处的电机车行驶路径为2、4、8、11，到达3#采场装载矿石后由12、9、4、1路径返回井底车场，卸载矿石后，矿车变为空闲状态，等待下一次运输命令。1#采场的运输路线为由2、5、6到达，7、5、1返回；到达2#采场有两条路径，从井底车场到采场可以走2、4、8、13或者2、5、6、14，1，装载矿石后可以由13、9、4、1或者14、7、5、1返回。

用变迁表示电机车每次状态的改变，包括出发、卸载以及进出某段进路等，用资源库所表示电机车对资源的占用情况，操作库所表示电机车的状态，建立如图2所示Petri网模型。

用计算机进行编程计算，按前文所述方法对此模型进行优化。计算时，每组参数进行10次运算。循环次数为100次，信息素更新规则参数ξ、ρ取0.1，伪随机比例参数q0取0.4，β取8时，运算效果较好，10次计算中有9次获得了相同的最优解5 270s，说明此方法是有效的。

5　结　语

结合Petri网理论，建立了基于蚁群算法和Petri网的矿山地下有轨运输调度优化模型。为了使模型能更好地适应于矿山地下有轨运输与时间和状态密切相关的特性，引入了时间戳状态类的方法，将蚁群算法中的信息素和启发式因子与时间戳状态类相关联。并且在其基础上建立了详细运行规则，包括变迁发生的条件、激发规则、信息素更新等。

图2　Petri网模型

参照蚁群算法的步骤，设计了优化计算的具体步骤，包括单次运行流程以及循环方法。通过多次循环计算，得出所需的优化结果，最后利用计算机编程进行具体实例的优化计算。结果表明，此算法快速有效，可以得出优化结果。

[1]潘理，李文军，刘显明.扩展时间戳状态类[J].系统仿真学报,2005,17(S1):73-77,81.

[2]袁崇义.petri网的原理与应用[M].北京：电子工业出版社,2005.

[3]WangJ,DengY,XuG.Reachabilityanalysisofreal-timesystemsusingtimePetrinets[J].IEEETransSystManCybernBCybern, 2000,30(5):725-736.

[4]李士勇.蚁群算法及其应用[M].哈尔滨:哈尔滨工业大学出版社,2004.

[5]潘理，郑红，郭观七，等.基于蚁群优化的时间Petri网及其在柔性制造系统调度优化中的应用[J].电子学报,2014,42(8):1531-1537.

[6]方欢，陆阳，徐自军，等.井下机车运输调度的资源分配模型及无死锁优化调度[J].系统工程理论与实践,2013(8):2087-2096.

OptimizationoftheUndergroundLocomotiveTransportationDispatchBasedonAntColonyAlgorithmandPetriNet

ZhuQihangZhouJieZhangWenju

(SchoolofResourcesandEnvironmentalEngineering,WuhanUniversityofTechnology)

Inordertosolvetheproblemofundergroundlocomotivetransportationdispatch,thePrtrinettheoryisintroducedtotheoptimizationofundergroundlocomotivetransportationdispatch,combingwiththebasicprincipleofantcolonyalgorithm,thetimedPetrinetmodelbasedonantcolonyalgorithmisestablished.Theantcolonyalgorithmmechanismisimproved,anditisusedtoanalyzethePetrinetmodel.Theclock-stampedstateclassimprovedbyundergroundlocomotivetransportationsystemisaddedtothePetrinetmodeltodealwiththerelationshipbetweentheoptimizationparametersofpheromoneandheuristicfactortotimeandstate,besidesthat,theoptimizationcalculationstepsareanalyzedandthecalculationprocessissimplified,theeffectivenessoftheaboveoptimizationmethodisverified.

Dispatchoptimization,Undergroundtransportation,TimedPetrinet,Antcolonyoptimization

2016-03-16)

朱启航(1991—)，男，硕士研究生，430070 湖北省武汉市。