基于ANSYS对大跨度混合梁斜拉桥的模态分析
王蓉 詹航
(1.重庆交通大学土木工程学院 重庆 400074;2.中铁大桥(南京)桥隧诊治有限公司 南京 210061)
基于ANSYS对大跨度混合梁斜拉桥的模态分析
王蓉1詹航2
(1.重庆交通大学土木工程学院重庆400074;2.中铁大桥(南京)桥隧诊治有限公司南京210061)
针对大跨度混合梁斜拉桥的力学特性问题,文章以拟建泸州长江六桥为研究背景,基于有限元软件ANSYS采用多种单元类型建立大跨度混合梁斜拉桥有限元模型,并对其进行了模态分析。在建模过程中,尽可能多地考虑了一些全桥有限元模型的精度因素:如单元划分的粗细程度,斜拉桥的几何非线性(重力垂度、初始应力)等等。研究结果表明:大跨度混合梁斜拉桥的高塔刚度较低,设计时需考虑索塔的稳定性问题;大跨度混合梁斜拉桥的主梁竖向刚度较其他各项刚度弱;改变主梁截面形式和索面布置可以提高结构的抗扭刚度。
混合梁斜拉桥;ANSYS;模态分析
0 引言
混合梁斜拉桥是指主梁沿长度方向由钢梁和混凝土梁通过钢混结合段连接而成的一类桥梁。其中,主跨采用钢梁,边跨或伸入主跨一部分梁体采用混凝土梁。由于主跨采用钢梁,故混合梁斜拉桥具有跨越能力大、经济效益好的特点。
近年来,我国混合梁斜拉桥的工程实例不断增加,如: 上海徐浦大桥、舟山桃夭门大桥、昂船洲大桥、鄂东长江大桥。为了减轻结构自重,有时主跨钢梁还会采用分离式双箱的截面形式,这使得主梁刚度大为降低,结构非线性突出,结构响应影响因素较多,故该类斜拉桥在设计时,对其结构的动力分析必不可少。
模态分析用于评价结构体系的动力特性,反映了结构的质量分布和刚度指标,模态分析结果为反应谱分析、动力时程分析提供基本的动力特征数据,因此对桥梁结构的抗震设计和抗风稳定性研究具有重要意义[1-2]。
本文以拟建泸州长江六桥为工程对象, 采用多种单元类型(空间梁单元、空间索单元和质量单元),根据设计图纸提供的物理特性和材料参数建立了泸州大跨度混合梁斜拉桥空间有限元模型,并对其动力特性进行分析。泸州长江六桥具有跨度大、三塔不等高、主梁采用较柔的混合梁等特点,其中主跨391m长的主梁采用的是分离式双箱截面形式。本文的研究进一步探明了大型复杂斜拉桥的力学性能,为同类斜拉桥的抗风稳定性、抗震设计提供了理论参考。
1 工程概况
泸州长江六桥是连接泸州城南副中心至城北副中心的重要过江通道,主桥为三塔混合梁斜拉桥,桥跨布置为(55+60)+2×425+(60+55)m。具体桥型布置见图1。
主跨主梁采用分离式钢箱梁,边跨采用整体式混凝土箱梁。全桥主梁设有四个钢-混结合段,分别在主跨距高塔中心线两侧18m处,距两低塔中心线16m处。低塔桥塔至桥台间的混凝土箱梁采用横向变宽的形式,从49m逐渐增至61.31m。

(a)主桥立面布置图图(b)MP4桥塔立面布置图图图1 泸州长江六桥桥型布置图(单位:cm)
斜拉桥三主塔不等高,均设置于桥面中央,横桥向为独柱形式,纵桥向采用分肢菱形造型。上塔柱为塔上锚固区,为实心混凝土结构,采用C60纤维混凝土,中、下塔柱则为空心截面。为了防撞的需要,将最高通航水位以上3.0m至高程247.4m区间塔柱空心部分用C20素混凝土填实。边跨设置两个辅助墩以减轻结构体系柔度。高塔采用塔梁固接形式,低塔设竖向支承。
高塔拉索区布置于人行道两侧,低塔则布置于中分带处。全桥共设84对斜拉索,跨中无索区长度为10.0m。高塔斜拉索纵向间距均为12.0m,低塔采用横向间距1.0m的平行索,钢箱梁段拉索梁端纵向间距为12.0m,混凝土梁段拉索梁端纵向间距为9.0m。
2 模态分析的基本理论
结构的动力响应受动荷载变化规律和结构的固有特性共同影响,不同的结构,若阻尼、频率和振型相同,则在相同的荷载下动力响应也相同。可见,结构的固有特性确定动荷载下的反应。模态分析的实质是一种坐标转换,即把原在物理坐标系统中描述的响应向量,放到“模态坐标系统”中来描述,这一坐标系统的每一个基向量恰是振动系统的一个特征向量[3]。因此,模态分析的关键在于得到振动系统的特征向量。结构体系的运动方程为[4]:
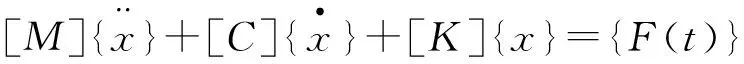
(1)
模态分析时取力向量为{0},即系统不受外力,且忽略阻尼,方程变为:
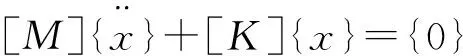
(2)
([K]-ω2[M]){x}={0}
(3)
式中:[K]为结构的刚度矩阵;[M]为结构的质量矩阵;{x}为结构的振型特征向量;ω2为振型特征值。
上式是振型{x}的齐次方程,求非零解,则需要系数行列式满足det([K]-ω2[M])=0。将行列式展开,可以得到一个关于频率参数ω2的n次代数方程。可见,振动特性分析归结为特征值问题。
ANSYS的模态分析是线性分析,任何非线性特性,如塑性和接触(间隙)单元 , 即使定义了也将被忽略[5]。但是,几何刚度的影响却不容忽略。
3 建立有限元计算模型
大桥计算模型采用ANSYS程序建立,全桥模型为鱼骨刺模型,其中,在分离双箱梁段建立两排主梁。主梁、墩和塔采用BEAM4梁单元,斜拉索采用LINK10单元。几个建模要点如下[5]:
(1)在模态分析中,唯一有效的“荷载”是零位移约束。
(2)静力求解时需打开大变形效应及应力刚化,动力求解时则要激活预应力影响,以考虑几何非线性影响。
3.1主梁的模拟
边跨混凝土梁段和主跨整体钢箱梁段建立单排主梁,主跨分离双箱梁段建立双排主梁,两排主梁间用刚臂相连。同理,分离式双主梁与整体式单主梁按刚接处理。主梁典型断面的截面参数如表1所示。
主梁质量系统主要考虑了主梁、横隔板、二期恒载、桥面铺装和防撞护栏等附属物,通过引入集中质量元来考虑其对主梁平动质量和转动惯量的贡献。
3.2索塔的模拟
在有限元模型简化中,虽然主塔划分单元的粗细对整桥的自振频率和塔根弯矩影响不大,但单元划分的粗细决定了集中质量的分布和振型的形状,对塔中间单元弯矩的分布影响较大,会影响桥梁结构的动力特性和内力分布[6-7],因此,这里将塔柱划分较细。表2列出了索塔部分典型断面的截面参数。下塔柱采用C20素混凝土夯实段,进行了截面换算。另外,桥塔与拉索锚固点不共节点,它们的连接用CERIG刚域命令处理。

表1 主梁典型断面的截面参数

表2 索塔典型断面的截面参数
3.3斜拉索的模拟
这里将柔性索视为直线杆件,计算时采用Ernst公式换算为等效弹性模量,近似地使非线性问题线性化。建模时用LINK10单元进行离散,将其处理为一个受轴向拉力的杆单元,初始应力则换算成初始应变作为实常数输入,单元初始应力为成桥时的索应力。
3.4边界条件的模拟
除结构的刚度和质量外,边界条件是动力特性的又一个主要决定因素。索塔及墩的桩基础均采用嵌岩桩基础,近似认为塔底及墩底固接。低塔采用竖向支承形式,建模时耦合主梁和桥塔的竖向自由度。主梁在边墩、辅助墩、边塔处均设置竖向支座和横向抗风支座,因此还必须约束相关横向自由度。高塔柱采用塔梁固接的形式,建模时对相关节点的6个自由度进行耦合。建立的整桥有限元模型如图2所示。

图2 泸州长江六桥有限元模型示意图
4 模态分析结果
运用有限元软件ANSYS对泸州六桥进行了模态分析,得出的结构动力特性为桥梁抗风与车桥振动分析提供了动力特征数据。一般结构前几阶的自振频率和振型起控制作用,所以本文只取前12阶自振频率和振型,如表3所示。
从表3动力特性分析结果可以看出,泸州六桥的固有振动振型主要表现为主梁竖弯、侧弯、扭转及塔的侧弯。因此这里列出主梁第一阶竖弯、侧弯、扭转振型即可,即第2、5、10阶振型,分别如图3~图5所示。
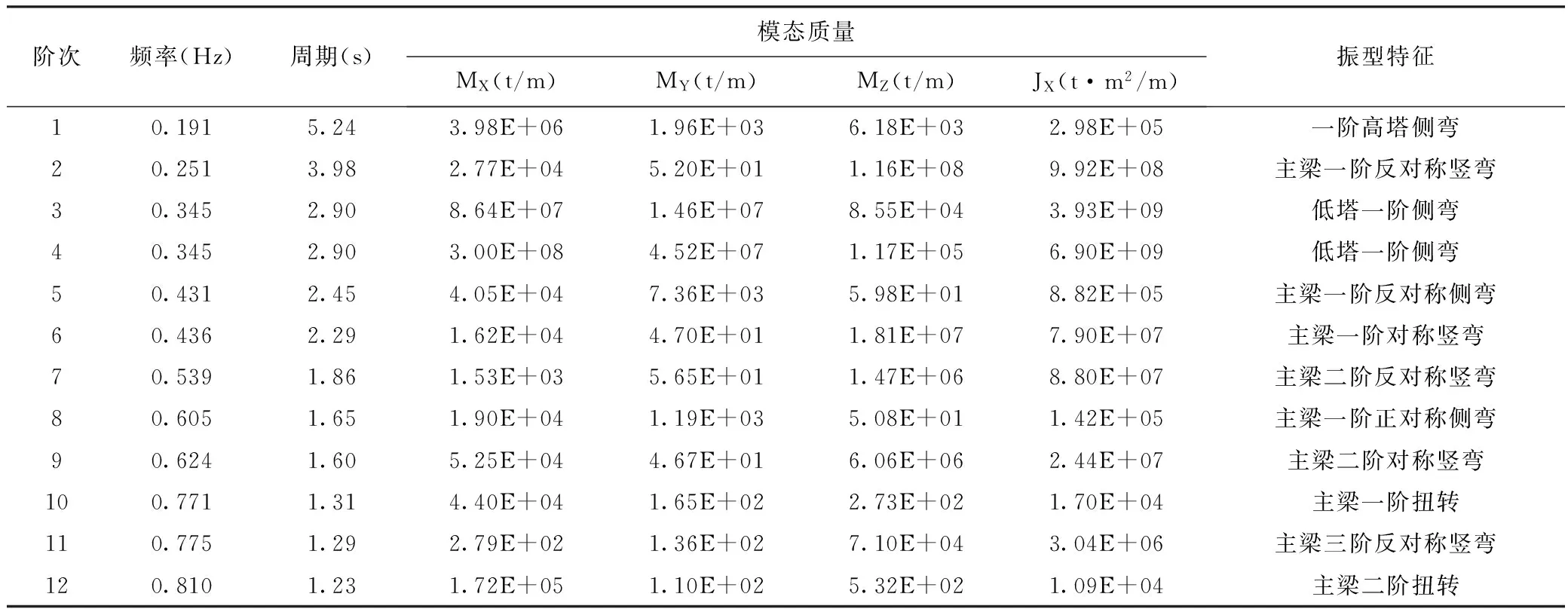
表3 成桥状态结构动力特性
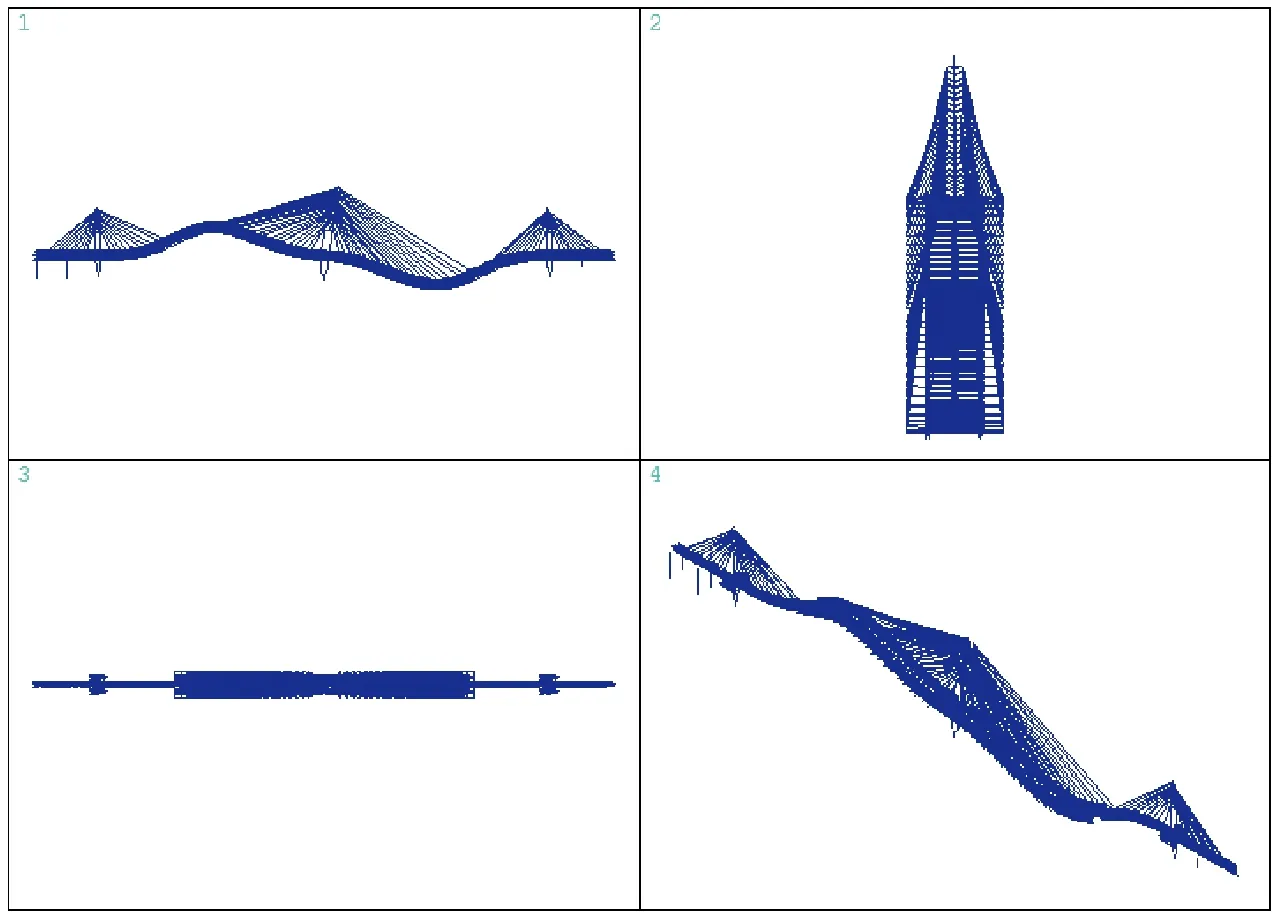
图3 第2阶振型图

图4 第5阶振型图
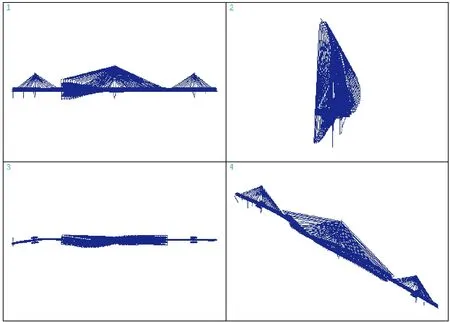
图5 第10阶振型图
经过图表的分析,总结出泸州六桥斜拉桥的动力特性的特点为:
(1)从表中数据可以看出,该斜拉桥的振动频率符合大型复杂结构的振动特性,即:各阶频率差值较小, 频率出现集聚现象。
(2)该桥高塔总高为184m,且有70m高的空心塔柱,抗弯刚度较弱,模态分析结果的基频振型表现为高塔侧弯正是验证了这一特征。两个低塔侧弯分别则出现在第三阶和第四阶,频率都高于高塔,说明该斜拉桥索塔的刚度较其他各项刚度稍弱,且塔柱越高,刚度越小。
(3)主梁一阶竖向振型出现在第二阶,频率为0.251Hz,而横向振动最早出现在第五阶,频率为0.430Hz,可见,主梁的竖向刚度比其他各项刚度稍弱。
(4)该桥的扭转振型为第10阶,频率为0.766Hz,出现在第二阶横向弯曲振型以后。这表明,主跨主梁采用刚度较弱的分离式双箱断面时,可通过将高塔拉索区布置于人行道两侧来改善扭转性能;同理,矮塔附近钢箱梁采用整体箱式,有助于提高矮塔拉索区布置于中分带处时主梁横向抗扭刚度。从动力特性角度来看,完全可以实现在减轻自重的情况下仍满足刚度设计要求。
(5)由图2及图5可以看出,同其他斜拉桥一样,泸州六桥的固有振动特性比较复杂,由于斜拉索的作用,侧向弯曲和扭转耦合在一起,故其结果不存在纯扭转的振型,而只有以侧弯为主兼有扭转的振型或以扭转为主兼有侧弯的振型。
(6)该桥为塔梁固接体系,第一阶振型不像漂浮体系那样表现为主梁纵向飘浮,基频相比同类桥梁较高为f1=0.191Hz,周期为T1=5.24s>5s,周期较长,横桥向地震动力响应最大时的自振周期为2.45s。故在抗震设计中,应注意隔震性能的加强。
5 结语
本文主要工作是根据原始设计图纸提供的材料及截面参数建立了泸州六桥的空间有限元模型,以模态分析理论为基础,对此有限元模型进行了模态分析,其结论如下:
(1)对于高塔斜拉桥,塔的刚度较弱,设计时要考虑索塔的稳定性问题。
(2)对于大跨度复杂斜拉桥,整个结构的竖向刚度比其他各项刚度稍弱,设计时要注意加强。
(3)通过改变主梁截面形式和索面布置相结合的方法,可以提高结构的抗扭刚度。
[1]熊文,肖汝诚,叶见曙. 超千米级CFRP与钢组合拉索斜拉桥动力性能分析[J]. 东南大学学报(自然科学版),2014,(5):1011-1016.
[2]王浩,乔建东. 桥梁结构动力特性的有限元分析与试验研究[J]. 公路交通科技,2004,(6):78-80.
[3]李德葆,陆秋海.实验模态分析及其应用[M]. 北京:科学出版社, 2001:1-18.
[4]R.W.克拉夫,J.结构动力学[M].彭津,译.北京:科学出版社,1985:136-138.
[5]王新敏. ANSYS 工程结构数值分析[M]. 北京:人民交通出版社, 2007:7-13, 501-503.
[6]蒋成强.部分斜拉桥索力研究与动力分析[D]. 兰州:兰州交通大学,2010.
[7]黎曙文,郭向荣,尹邦武.曲率半径对矮塔斜拉桥车桥耦合振动影响研究[J].铁道科学与工程学报,2014,(2):28-34.
Modal Analysis of Long Span Hybrid Girder Cable- stayed Bridge Based on ANSYS
WANG Rong1ZHAN Hong2
(1.College of Civil Engineering,Chongqing Jiaotong University, Chongqing 40074;2.China Railway Major Bridge(Nanjing)Bridge and Tunnel Inspect & Retrofit Co.,Ltd,Nanjing 210061)
For the problem of mechanical properties of the large span cable-stayed bridge, this paper took the Luzhou Yangtze River Bridge as the research background, ANSYS would be applied to develop a finite element model of the large span cable-stayed bridge by using a variety of cell types. And the model was used into modal analysis. In the modeling process, some accuracy factors of the finite element model of the whole bridge is considered as much as possible, such as the degree of unit division, the geometric nonlinearity of cable-stayed bridges (gravity sag, initial stress), etc.. Based on above analysis, the stability of tower should be taken into consideration due to the low rigidity. Furthermore, vertical rigidity is the most fragile part of main beam exists commonly in long span cable--stayed bridges. Torsional rigidity can be improved by changing the section form and cable plane arrangement of main beam.
Hybrid girder cable-stayed bridge;Ansys;Modal analysis
王蓉(1992.3-),女。
E-mail:517239048@qq.com
2016-05-18
U443
A
1004-6135(2016)08-0095-05

