适用于多方协议的可否认认证

陈勇，鲁龙，曾晟珂，何明星

（西华大学计算机与软件工程学院，四川 成都 610039）

适用于多方协议的可否认认证

陈勇，鲁龙，曾晟珂，何明星

（西华大学计算机与软件工程学院，四川 成都 610039）

可否认认证不仅可以像数字签名那样实现消息认证，且非公开可验证性使其可以满足许多签名不能满足的需求，如隐私保护等。研究了如何在多方协议中实现完全可否认认证，利用承诺方案提出了一个适用于多方协议的可否认认证。该方案作为一种一般化的方法，能够为大多数多方协议实现可否认认证，如可否认的群密钥协商协议等，形式化了方案的敌手模型并严格证明了方案的安全性，为研究可否认认证提供了一种新思路。

可否认认证；多方协议；承诺；安全性

1　引言

数字签名作为密码学的一种基本原语，其不可伪造性以及不可否认性受到学术界的广泛关注。由于签名过程的不可抵赖性，数字签名算法不适用于保护用户隐私的认证。为了保护认证过程中用户的隐私，可否认认证的概念被提出。可否认认证协议在保证消息认证性的同时，其认证副本并不能证明协议的参与者参与了认证，即不具有公开验证性，这在电子购物、互联网会议等方面有广泛的应用前景。

1998年，Dwork等［1］首次正式提出可否认认证的概念，并利用时间约束机制实现了并发环境中的可否认认证。之后一系列的可否认协议被提出［2～4］。交互式的认证主要面临并发会话攻击。认证的可否认性要在并发环境中成立，一般采用时间约束机制［1］，然而，这种假设太强。通过使用Pass在文献［5］中提出的非编程预言机，Jiang等［6］提出一个不使用时间约束的在并发环境中完全可否认的认证协议。Raimondo等在文献［7］中利用明文可意识性（plaintext awareness）证明了SKEME协议满足完全可否认性。Jiang［8］利用“时限加密”，在可认证的密钥交换协议中实现了可否认性。

为了提高认证协议的效率，很多学者关注认证协议的交互轮数，提出了一系列非交互式可否认的认证协议［9～11］。由于非交互性，这些协议自然满足并发环境，但却仅实现“半可否认性”［5］。例如，Susilo在文献［9］中利用 Chameleon Hash函数实现认证的可否认性，在文献［9］方案中，参与方只能否认通信的内容，却不能否认其参与了认证。Li等［11］也提出了一种非交互式的、基于身份的可否认认证协议。该协议也仅达到了半可否认性，因为只有消息接收方才能仿真发送方发的认证副本。即对于某次认证副本，发送方和接收方中至少有一方不能否认参与了认证。可见，非交互式的可否认认证虽然认证效率较高，但是应用限制大。

在这些方案中，研究者研究的模型大多都是一对一的，即一对消息的发送者与接收者。在一些实际应用中，协议需要多方用户的参与。在多方协议中引入可否认认证有以下研究工作。2002年，Naor［12］将可否认认证与环签名的特性相结合，提出了可否认的环认证，消息的接收者能够确认消息确实来自环中的成员，但不能确认具体是哪一个成员，同时，第三方却不能确认消息来自于环成员。另一个将可否认认证引入到多方环境的协议是可否认的群密钥协商协议，可否认的群密钥协商协议是指多个参与者通过协商得到一个共同的会话密钥，在协商结束后，任何实体都不能证明协商的参与者曾经参与了协议。2006年，Bohli等［13］利用Schnorr签名算法［14］首次提出一个可否认的群密钥协商协议，并在Random模型中证明协议的安全性。2010年，Zhang等［15］改进了文献［14］中方案的通信效率，且安全性证明不需要随机预言机；2010年，Zhang等［16］给出一个构造可否认群密钥协商协议的一般构造方法，该方法可以将无认证的群密钥协商协议转化成可否认的群密钥协商协议。2014年，Steinwandt等［17］提出一个构造器可以将一个普通的两轮次的群密钥协商协议转化为一个三轮次的可否认的群密钥协商协议。2016年，Chen等［18］利用DB协议［19］提出一个可否认的群密钥协商协议，进一步改进了协议的通信效率。

目前，虽然已有一系列关于可否认的群密钥协商协议的研究，但其可否认性都依赖于最终的会话密钥协商，无法简单地将其扩展到普通的多方协议，如非对称的群密钥协商协议［20］等。因此，本文旨在通过秘密承诺［23］的思想设计一个适用于广播信道（如ad hoc网络等）中多方协议的可否认认证方案（MDA， deniable authentication for multi-party protocol）。与以往的多方可否认认证（如可否认的群密钥协商）方案不同，本文方案不再关心消息的具体内容，因此，具有很好的扩展性。另外，本文定义了MDA方案的敌手模型，并对方案的安全性给出了证明。

2　基础知识

2.1困难性问题

本文的安全性主要是基于判定性 Diffie-Hellman（DDH）假设。令G为阶是素数q的乘法群，g是群G的生成元。

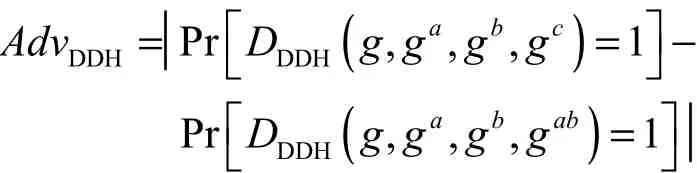
2.2多方计算协议

在只存在被动敌手的公共信道上，给出多方协议［21］的一般定义。令P1， …， Pn表示信道中的n个对等用户，q表示系统的安全参数。假设协议共执行l个轮次，则多方协议的基本通信模型如下。

1）参与方Pi选择xi作为自己的输入，同时选择一个随机值ri。

2）令t=1，参与方Pi依次执行以下步骤，直到t≥l。

① Pi产生消息其中，表示在本轮次将要发送给参与方的消息。

③令t=t+1。

3）参与方Pi产生输出oi。

在只存在被动敌手的情况下，多方协议只需满足私密性，即当存在敌手监听整个信道时，参与方Pi所产生的输出oi只能被它自己所了解。然而，当信道中存在主动敌手时，主动敌手可以插入、删除、篡改任何消息。此时，协议不仅需要满足私密性，还必须满足认证性。

私密性：参与方Pi产生的输出oi只能被参与方自己所了解，而对于任何第三方来说，oi在参数空间内是均匀分布的。

认证性：在多项式时间内，任何敌手都不能以不可忽略的概率伪装成其他诚实参与方参与并完成协议。

最常见的多方协议的例子便是群密钥协商协议。

2.3字符串承诺方案

承诺方案作为一种基础性密码工具，常被用在构造零知识证明［22］或可否认认证中。在承诺方案中，承诺者将承诺值和秘密值绑定在一起，承诺结束后，承诺者打开秘密值并验证。安全的承诺方案必须满足私密性和绑定性。字符串承诺方案［22］一般由以下几个算法组成。

1）初始化阶段Gen（1）k：可信方运行初始化算法生成系统参数（p，g，h）。

私密性：在承诺值被打开之前，承诺值保持私密性。

3　模型

3.1相关符号

首先，给出方案所用的主要符号，如表1所示。

表1　相关概念

3.2系统模型

本方案的基本思想是：在协议开始初，参与者承诺一个消息认证码密钥；然后，参与者利用私钥对消息认证码密钥进行签名；接着，参与者利用消息认证码密钥对多方协议的通信进行认证，这里需要认证编码函数MAC；在协议结束后，参与者公开自己的消息认证码密钥，其他参与者验证多方协议消息的合法性。

因此，MDA方案包括6个算法，下面对各个算法进行介绍。

t进行认证。

需要注意的是，Communicate阶段不需要在Commit阶段和Authenticate阶段之后，可以在这2个阶段之前或之间。为了达到较高的通信效率，Communicate阶段一般与Commit阶段和Authenticate阶段同时进行。

3.3 安全模型

MDA方案使每个用户确信收到的消息的确来自诚实用户，且发送者对消息的认证是可否认的，因此，其安全性包括完整性、健壮性、可否认性。

1） 完整性。如果所有的参与者都诚实地执行协议，则jPpid∈接受消息tim来自用户iP。

2） 健壮性。方案的健壮性意味着任何用户都不能伪装成诚实用户iP对消息tim进行认证。接下来，通过一个游戏来定义方案的健壮性。

初始化阶段：挑战者X运行Setup（1）k生成系统参数，并将公开的系统参数发送给敌手A。

训练阶段：挑战者X回答敌手A的一系列查询。

3） 可否认性。方案的可否认性是指协议的通信副本可以由敌手独自构造出来。即存在一个仅了解敌手知识的模拟者，不能访问用户的私钥，除非用户被腐蚀，构造的通信副本的分布与真实通信的分布是一致的。正式地说，用表示模拟者模拟的通信副本，用表示真实执行过程的副本，令∆表示某个多项式时间的区分者，给出以下可否认的定义。如果对于任何的敌手 A和所有的区分者∆，总存在一个模拟者，使则认为协议是满足可否认的。

4　协议的实现

本节给出MDA方案的具体实现，方案的灵感来源于文献［1］的零知识证明。下面给出方案的详细过程。

Setup：k为系统的安全参数；G是一个阶为素数q的乘法群；g是群G的生成元；H是一个密码学散列函数

5　安全性证明

本节对方案的安全性进行证明，很容易理解方案是满足完整性的，所以，接下来分别证明方案的可否认性和健壮性。

5.1可否认性

MDA方案的可否认性使参与者可以否认曾经参与了多方协议消息的认证，即参与者可以否认曾参与了多方协议。本文通过构造一个模拟者∑，在不允许模拟者∑访问未腐蚀用户私钥的情况下，显示模拟者生成的通信副本与真实执行过程的通信副本不可区分，从而证明方案是满足可否认性的。

定理1MDA方案满足可否认性，如果H是一个随机预言机。

证明构造模拟者∑，它的输入仅包括用户公钥等公共参数以及被腐蚀用户的私钥。用表示破坏方案可否认性的敌手。在模拟过程中，模拟者必须回答敌手的一系列询问，如Commit、Authenticate、Communicate、Open以及Corrupt。用表示在模拟过程中的通信副本，用表示真实协议的执行副本。可否认性显示对于任何敌手和所有的区分者∆，都存在一个模拟者，使和是不可区分的。

Open（i,l1）：模拟者∑公开承诺值，即广播消息

显然，模拟者∑能够在不引起任何区别的情况下成功地回答敌手的所有查询，所以，该方案实现了可否认性。

5.2健壮性

方案的健壮性是指任何敌手，在不了解用户iP私钥的前提下，都不能伪装成用户Pi参与协议。本文显示，如果一个敌手能够破坏方案的健壮性，则该敌手一定能以不可忽略的概率解决DDH困难性问题。

定理2如果DDH困难性假设成立，且消息认证编码函数（）MAC⋅是安全的，H是一个随机预言机，那么方案是满足健壮性的。

证明用A表示攻击方案健壮性的敌手，如果A能以不可忽略的概率攻破方案的健壮性，则挑战者X就可以利用敌手A来解决DDH困难性问题。挑战者X被给出实例，判断与是否相等。

接下来，说明挑战者X如何利用敌手A来解决困难性问题。

接下来，敌手开始进行游戏，首先是训练阶段，具体如下。

H查询：挑战者X维持一个初始化为空的列表listH。当输入消息mi时，挑战者X检查listH里是否存在（mi，θi）。如果存在，则返回θi；否则，挑战者 X随机地选择θi，同时将（mi，θi）存入到listH中并返回θi。

经过一系统的训练之后，敌手A提交挑战查询，挑战部分如下。

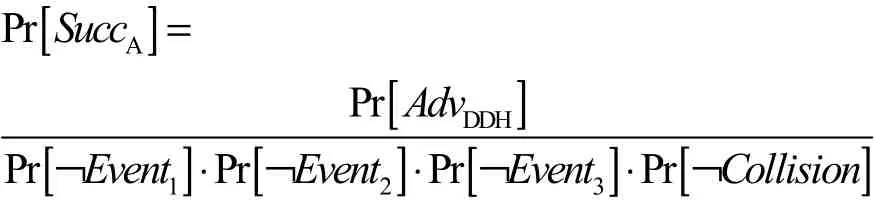
6　结束语

本文提出了一个适用于多方协议的可否认认证方案，MDA协议可以有效地防止敌手对通信的消息进行修改或插入，从而冒充合法用户去欺骗其他诚实用户。同时，区别于数字签名的不可否认性，即公开可验证性，可否认协议的通信副本不能证明用户曾经参与了协议，有效地保护了参与者的隐私。本文在前人的基础上，形式化了方案的敌手模型，并证明了方案满足可否认性和健壮性。相比于可否认的群密钥协商协议等具体方案，本文方案具有很好的扩展性，能够被应用到多数多方协议中实现可否认认证。

［1］DWORK C， NAOR M， SAHAI A. Concurrent zero-knowledge［J］. Journal of the ACM， 2004， 51（6）：851-98.

［2］DENG X， LEE C H， ZHU H. Deniable authentication protocols［J］. IEEE Computers and Digital Techniques， 2001， 148（2）：101-104.

［3］LEE W B， WU C C， TSAUR W J. A novel deniable authentication protocol using generalized ElGamal signature scheme［J］. Information Sciences， 2007， 177（6）：1376-1381.

［4］KAR J. ID-based deniable authentication protocol based on diffie-hellman problem on elliptic curve［J］. International Journal of Network Security， 2013， 15（5）：357-364.

［5］PASS R. On deniability in the common reference string and random oracle model［C］//Advances in Cryptology， Berlin. c2003：316-337.

［6］JIANG S. Deniable authentication on the Internet［M］. Berlin：Springer， 2008：298-312.

［7］RAIMONDO M D， GENNARO R， KRAWCZYK H. Deniable authentication and key exchange［C］//ACM Conference on Computer and Communications Security. c2006：400-409.

［8］JIANG S. Timed encryption with application to deniable key exchange［J］. Theoretical Computer Science， 2014（560）： 172-189.

［9］SUSILO W， MU Y. Deniable ring authentication revisited［C］// Applied Cryptography and Network Security， Berlin. c2004：149-163.

［10］WANG L， ZHANG G， MA C. ID-based deniable ring authentication with constant-size signature［J］. Frontiers of Computer Science in China， 2008， 2（1）：106-12

［11］LI F， XIONG P， JIN C. Identity-based deniable authentication for ad hoc networks［J］.Computing， 2014，96（9）： 843-853.

［12］NAOR M. Deniable ring authentication［C］//Advances in Cryptology， Berlin. c2002：481-498.

［13］BOHLI J M， STEINWANDT R. Deniable group key agreement［C］//Progress in Cryptology， Berlin. c2006：298-311.

［14］SCHNORR C P. Efficient identification and signatures for smart cards［C］//Advances in Cryptology， Berlin. c1989：239-252.

［15］ZHANG Y， WANG K， LI B. A deniable group key establishment protocol in the standard model［C］//Information Security， Practice and Experience， Berlin. c2010： 308-323.

［16］张雅哲， 徐海霞， 李宝. 可否认群密钥协商协议的一般化构造方式［J］. 通信学报， 2011，32（3）：143-149. ZHANG Y Z， XU H X， LI B. But denied group key agreement protocol way of generalized structure［J］. Journal of Communications， 2011， 32（3）： 143-149.

［17］STEINWANDT R， CORONA A S. Scalable attribute-based group key establishment： from passive to active and deniable［J］. Applicable Algebra in Engineering， Communication and Computing， 2014，25（1/2）：1-20.

［18］陈勇， 何明星， 曾晟珂， 等. 两轮次的可否认的群密钥协商协议［J］.密码学报， 2016，3（2）：137-146. CHEN Y， HE M X， ZENG S K， et al. Two rounds of deniable group key agreement protocol［J］. Journal of Password， 2016， 3（2）：137-146.

［19］DUTTA R， BARUA R. Provably secure constant round contribu-tory group key agreement in dynamic setting［J］. IEEE Transactions on Information Theory， 2008， 54（5）：2007-2025.

［20］CHEN Y， HE M， ZENG S， et al. Universally composable asymmetric group key agreement protocol［C］//The 10th International Conference on Information， Communications and Signal Processing（ICICS）， IEEE. c2015.

［21］CANETTI R. Security and composition of multiparty cryptographic protocols［J］. Journal of Cryptology， 2000， 13（1）：143-202.

［22］FEIGE U， FIAT A， SHAMIR A. Zero-knowledge proofs of identity［J］. Journal of Cryptology， 1988， 1（2）：77-94.

［23］CHAUM D， HEIJST E V， PFITZMANN B. Cryptographically strong undeniable signatures， unconditionally secure for the signer［C］//The 11th Annual International Cryptology Conference on Advances in Cryptology. c1991：470-484.

Deniable authentication for multi-party protocol

CHEN Yong， LU Long， ZENG Sheng-ke， HE Ming-xing

（School of Computer and Software Engineering， Xihua University， Chengdu 610039， China）

Deniable authentication can authenticate messages like digital signatures， and its non-public verification can meet many requirements that cannot be met by signatures， such as privacy preservation. How to achieve deniable authentication with multi-party protocol was the study aim. A deniable authentication for multi-party protocol using string commitment scheme was proposed. As a generic method， it can pass the most of protocol to deniable protocol， such as the deniable group key agreement protocol. The adversarial model was formalized and the security was proved strictly. The research content provide a new idea for studying deniable authentication.

deniable authentication， multi-party protocol， commitment， security

TP393

A

10.11959/j.issn.2096-109x.2016.00059

2015-04-17；

2015-05-25；通信作者：陈勇，chenyong.sclz@gmail.com

国家自然科学基金资助项目（No.61402376， No.U1433130）；四川省高校重点实验室开放课题基金资助项目（No.SZJJ2014-078）；国家科技支撑计划基金资助项目（No.2011BAH26B04）；教育部春晖计划基金资助项目（No.Z2014045）

Foundation Items： The National Natural Science Foundation of China （No.61402376， No.U1433130）， The Open Research Foundation of Key Laboratory of Colleges and Universities in Sichuan Province （No.SZJJ2014-078）， National Science and Technology Support Program （No.2011BAH26B04）， Chunhui Project of the Ministry of Education of China （No.Z2014045）

陈勇（1991-），男，四川阆中人，西华大学硕士生，主要研究方向为密码与信息安全。

鲁龙（1989-），男，山东临沭人，西华大学硕士生，主要研究方向为密码与信息安全。

曾晟珂（1982-），女，四川成都人，博士，西华大学讲师，主要研究方向为密码与信息安全。

何明星（1964-），男，四川巴中人，博士，西华大学教授，主要研究方向为密码与信息安全。