复杂山地风速频率分布和风能密度分布研究
■陈桂宝邓胜祥(1.中南大学能源科学与工程学院;2.长沙理工大学可再生能源电力技术湖南省重点实验室)
复杂山地风速频率分布和风能密度分布研究
■陈桂宝1*邓胜祥1,2
(1.中南大学能源科学与工程学院;2.长沙理工大学可再生能源电力技术湖南省重点实验室)
选用我国中部某复杂山地80 m测风塔高度处一个完整年的实测数据,结合Weibull分布、Rayleigh分布和对数正态分布3种不同风速频率分布模型计算风速频率,与实测风速频率分布对比并进行相关性分析,然后根据风速频率分布计算风能密度分布,与实测风能密度分布对比并进行误差分析。结果表明,复杂山地中Weibull分布模型对风速频率拟合性较好且计算风能密度误差较小。因此,在复杂山地风速频率分布和风能密度分布研究中,应采用Weibull分布模型。
复杂山地;风速频率分布;风能密度分布;模型;Weibull分布
0 引言
目前,世界能源正处在关键的转型时期,各国政府都提出了明确的能源转型战略,并积极发展新能源和可再生能源。在新能源和可再生能源中,风能得到大力发展,开发利用技术亦日趋成熟[1]。风能最主要的利用方式为风力发电,因此需要建设风电场。在风电场建设的前期工作中,风能资源评估必不可少,其中,风速频率分布和风能密度分布是确定风电场建设可行性的两个重要指标。
近年来,平原地区和沿海地区风电场建设速度迅猛,风电场数量接近饱和,而内陆地区复杂山地风能资源丰富,但开发利用程度较低,可开发利用空间很大[2]。山地地形复杂,道路崎岖,为降低风电场建设成本,必须进行详实的风电场规划,而风速频率分布和风能密度分布是两个非常重要的指标[3],直接影响到风电场发电量的估算,进而影响经济效益的评估。随着风能利用的不断发展,复杂山地风速频率分布和风能密度分布的研究越来越受重视。风速频率分布可用一定的统计模型进行拟合[4],而风能密度分布可基于风速频率分布模型计算得出。
本文结合Weibull分布模型、Rayleigh分布模型和对数正态分布模型,以我国中部某复杂山地80 m高度处一年实测数据对风速频率分布和风能密度分布进行研究,判断该地区风速频率分布和风能密度分布的规律,验证复杂山地风速频率分布和风能密度分布的研究中,采用Weibull分布模型的准确性。
1 风速频率分布
1.1风速频率定义
风速频率表征各风速区间内风速出现的频率,是风能资源评估和风电场规划设计中的一个重要参数,能很好地描述风电场场址处风能资源的状况,并直接影响风电场建设中风机选型、发电量估算和经济效益评估。已知实测风速数据,其计算公式为[3]:

式中,n为统计观测时段内风速序列个数;i为风速区间内风速序列个数。
1.2风速频率分布模型
风电场一般选择建设在风能资源相对丰富的地方,如平原地区、沿海地区和内陆山地。风电场所在地气候、地理情况各异,风速数据和风速频率分布参数均为随机数据,其内部之间具有时序性,也具有一定相关性。因此,对于风速频率分布可根据时间序列给出的实测风速数据进行统计分析处理,研究风速发展的变化情况,包括发展速度和发展趋势,并探究风速变化的规律性[5,6]。
由于风速特性和风速分布形式多样化,可采用多种风速频率分布模型对风能资源分布情形进行拟合[7]。描述风速频率分布特性的模型有多种,可利用其预测各月风速频率分布和风能密度分布。目前常用的模型有Weibull分布模型、Rayleigh分布模型和对数正态分布模型等。
1.2.1Weibull分布模型
Weibull分布模型对各种频率分布具有很强的适应性,能很好地描述风速频率分布,对应风速v的频率分布函数为:
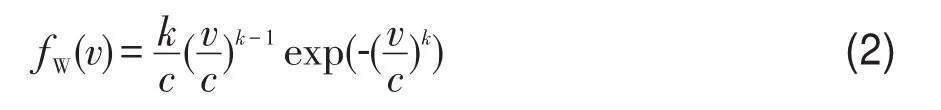
式中,k为形状参数,1<k<3;c为尺度参数。
k、c根据实测风速数据,可采用最大似然法求得[8-10],公式为:
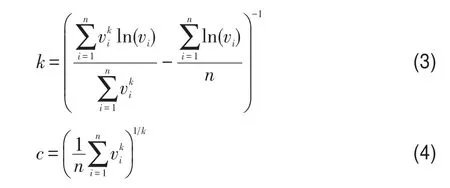
式中,vi为时间序列给出的风速。
1.2.2Rayleigh分布模型
当Weibull分布模型中k=2时,得到Rayleigh分布模型,其风速频率分布函数为:
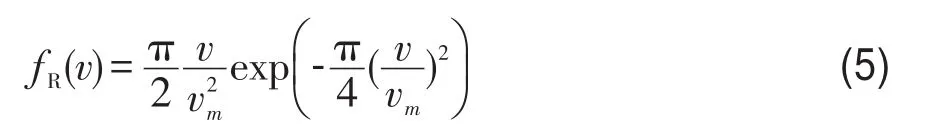
式中,vm为某一时间段的平均风速,计算公式为:


因此,Rayleigh分布模型只要已知vm便可求得风速频率分布。
1.2.3对数正态分布模型
在风速频率分布研究初期,常用对数正态分布模型进行拟合,函数为:
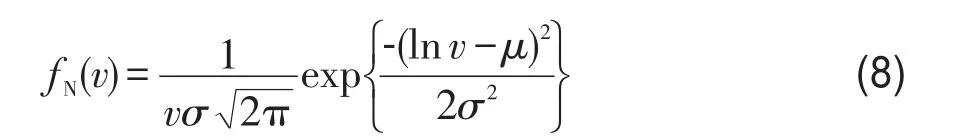
式中,σ为形状参数;μ为尺度参数。
σ和μ的计算公式为:
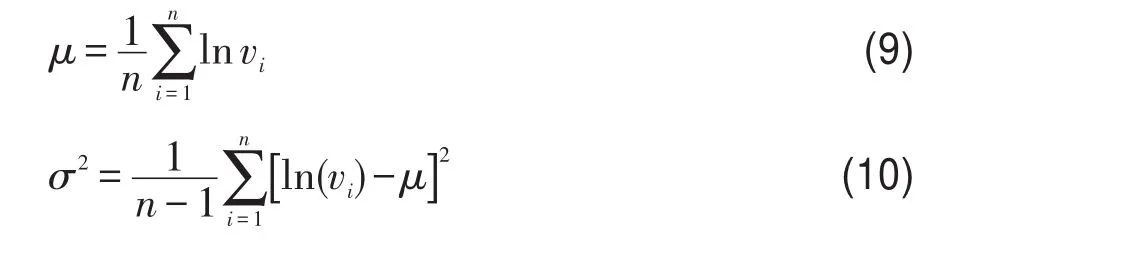
2 风能密度分布
2.1风能密度定义
我以为她捞几下就不捞了,但她竟然甩了鞋子,把衣袖往上捋捋,卷起来,下了水。靠岸的麦麸捞完了,她又向水中央游去。
风能密度表征在单位时间内通过单位面积的风能,是描述风能潜力的一个重要参数,其计算公式为:

式中,ρ为空气密度。由于风速数据随机动态变化,使用瞬时风速计算得到的风能密度不能反映其规律,需在长期风速观察的基础上,计算平均风能密度。
2.2风能密度计算方法
PM为平均风能密度参考值,由实测数据计算平均风能密度的公式为[11,12]:

1)由Weibull分布模型计算平均风能密度的公式推导如下:
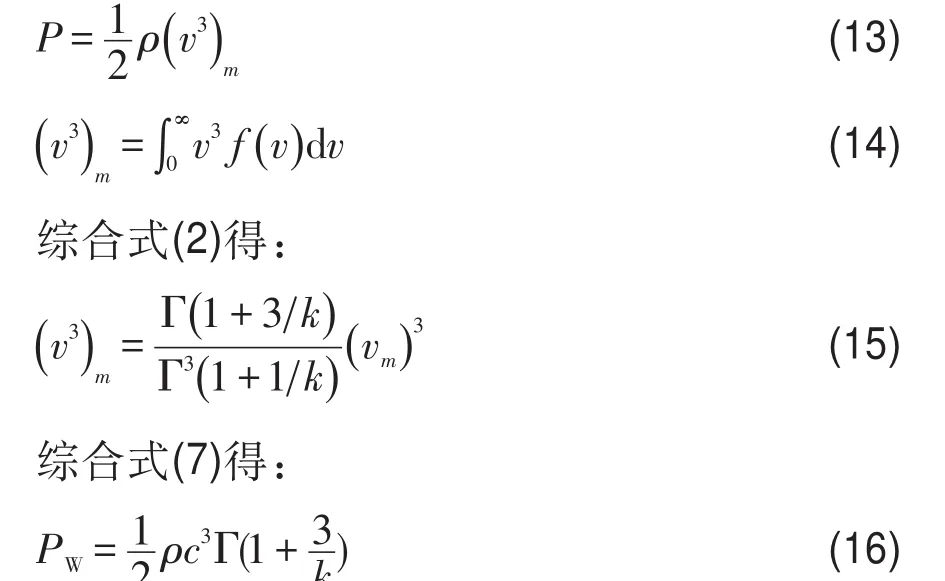
2)当k=2时,得到Rayleigh分布模型计算平均风能密度的公式为:

3)由对数正态分布模型计算平均风能密度的公式推导,由式(14)综合式(8)得:
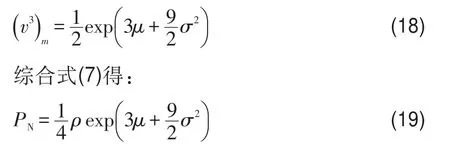
3 计算实例
3.1数据来源及介绍
数据选用我国中部某海拔高于1000 m山区的一座测风塔80 m高度处,2013年1~12月一个完整年的测风数据。地形属于复杂山地,山脊为东北西南走向,山体连绵起伏,上山道路较长且较为陡峭,山体较薄,山顶窄而尖,植被多为灌木,年平均气温约为13℃,如图1所示。
风速仪每10 min记录一组数据,修正后共有52560组。经计算,全年平均风速为5.05 m/s,各月根据实测数据算得统计分布参数如表1所示。
图1 复杂山地地形图
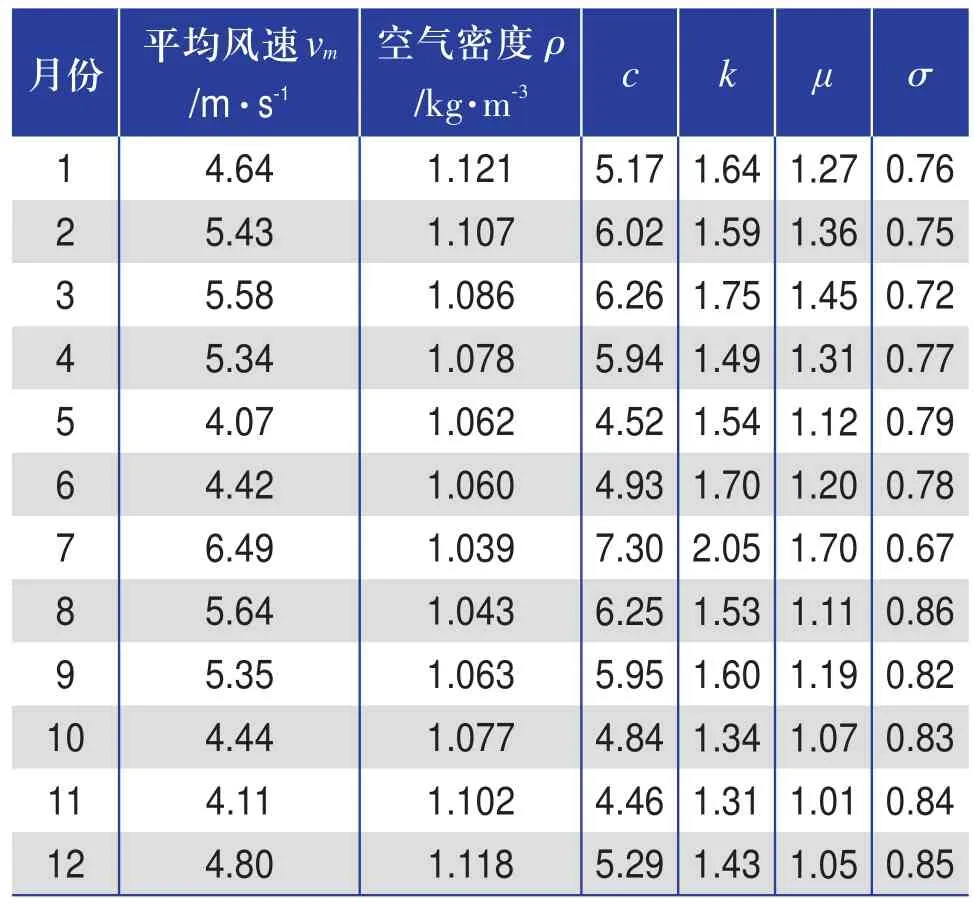
表1 由实测数据计算出的风速统计分布参数
3.2风速频率分布计算
先以7月份实测数据计算风速频率分布,然后使用Weibull分布模型、Rayleigh分布模型和对数正态分布模型分别计算风速频率分布,计算结果如表2所示。图2为7月份按实测数据计算和按各模型计算的风速频率分布对比图。
由表2和图2可以看出,3种模型计算的7月份风速频率分布曲线形状大体相同,频率集中的风速段相似,均可定性反映风速分布情况。对比3种模型计算结果,Weibull分布模型计算的风速频率分布和实际风速频率分布拟合效果最好,其次是Rayleigh分布模型,对数正态分布模型拟合效果最差。
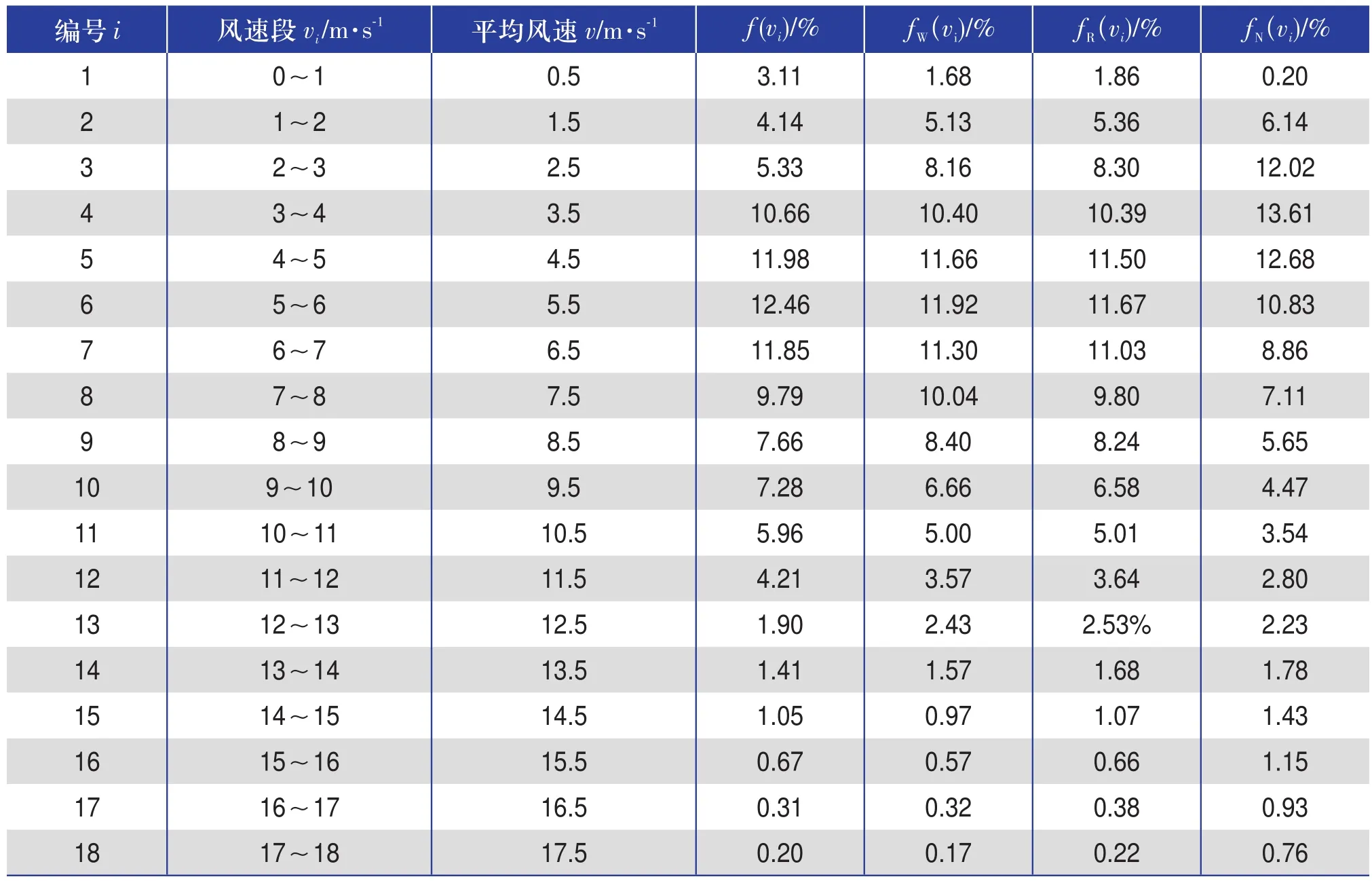
表2 实测数据和模型计算出的7月份风速频率分布
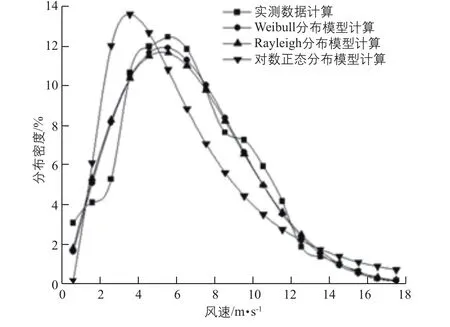
图2 7月份风速频率分布对比
对各月风速频率分布进行相关性分析[13],计算公式为:

3种模型各月相关系数如图3所示。
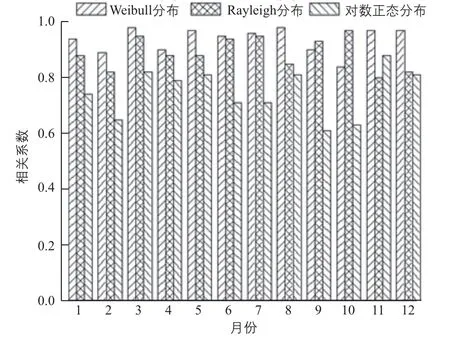
图3 各月相关系数对比
由图3可以看出,在复杂山地中,Weibull分布模型相关系数总体高于Rayleigh分布模型,而Rayleigh分布模型相关系数总体高于对数正态分布模型,说明Weibull分布模型对实测数据的总体拟合性最好,Rayleigh分布模型次之,对数正态分布模型在3种模型中拟合性最差。特别的是,9月、10月Weibull分布模型对实测数据拟合性反而比Rayleigh分布模型差,估计是由于这两个月山地风风向多变、大小也不稳定所致。
3.3风能密度分布计算
由风能密度分布计算方法,分别计算各月和全年风能密度。各月风能密度如图4所示。全年风能密度的实测值、Weibull分布模型计算值、Rayleigh分布模型计算值和对数正态分布模型计算值分别为173.13、179.83、137.95、180.36 W/m2。
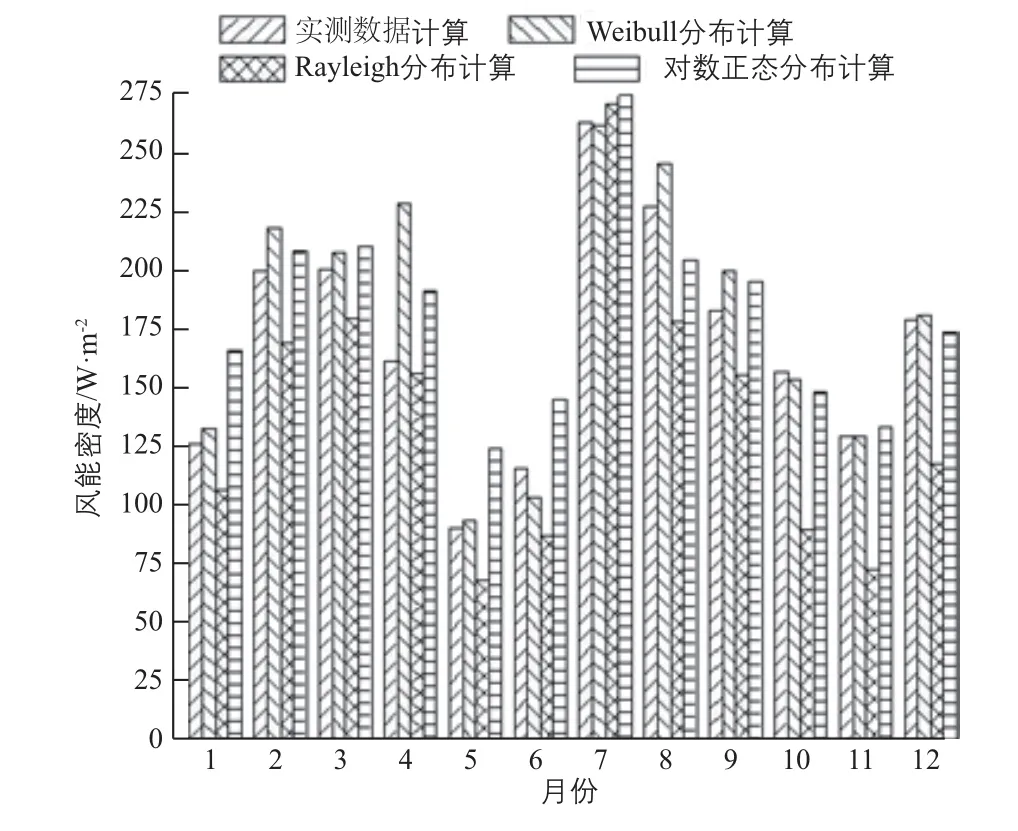
图4 各月风能密度分布对比
各月风能密度模型预测值和实测值误差的计算公式为:

表3为各月误差计算结果,可看出,在复杂山地中,Weibull分布模型计算风能密度误差最小,对数正态分布模型次之,Rayleigh分布模型误差最大。Weibull分布模型最小误差发生在11月份,为0.20%;最大误差发生在4月份,为12.16%;年均误差为3.24%。对数正态分布最小误差发生在12月份,为-2.80%;最大误差发生在5月份,为37.25%;年均误差为9.21%。Rayleigh分布模型误差相对较高,最小误差为2.88%,最大误差则达到40%以上,年均误差为-22.27%。这点区别于在平坦地形中得出的Rayleigh分布模型计算风能密度误差小于对数正态分布模型计算风能密度误差的结论。
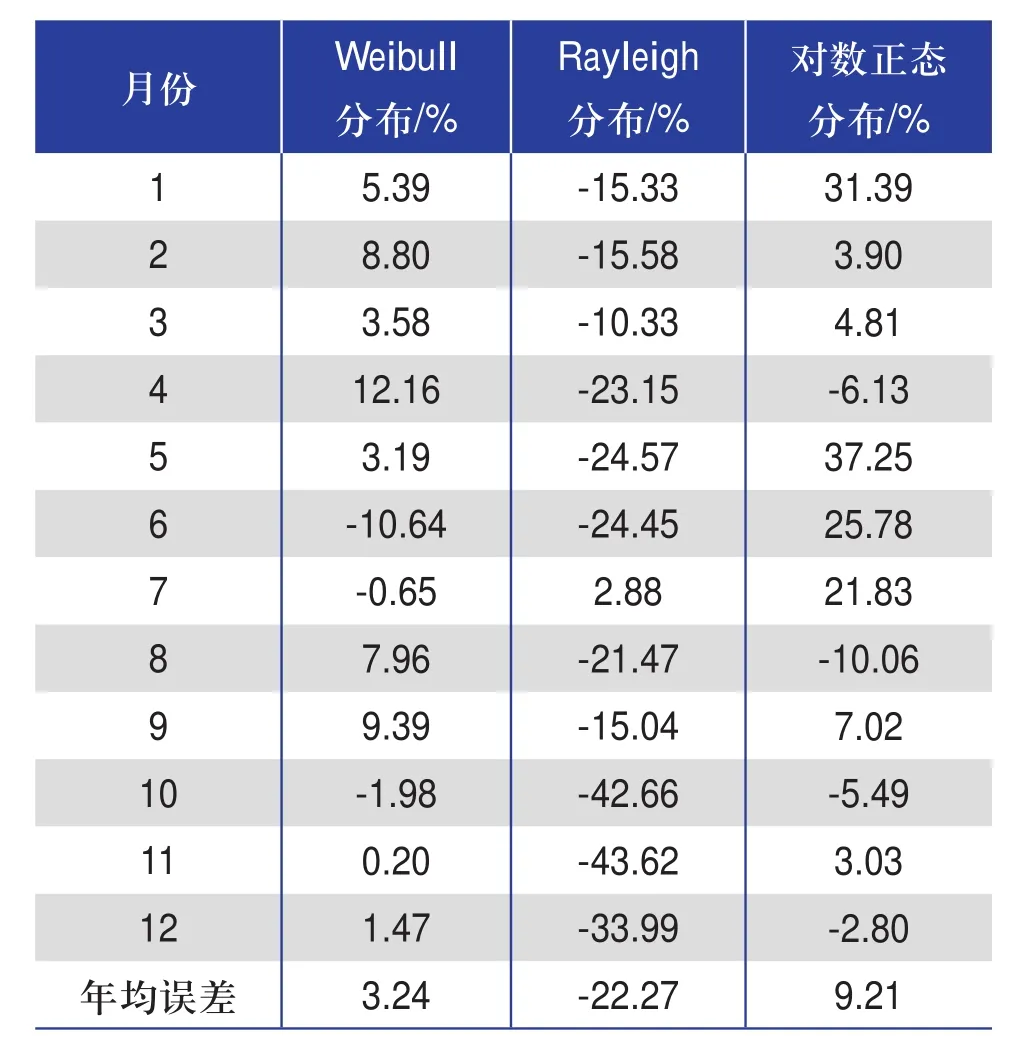
表3 各月风能密度模型预测值误差
4 结论
1)通过比较实测数据计算的风速频率和由不同分布模型计算风速频率,发现在复杂山地中采用Weibull分布模型计算的结果和实测数据计算的结果总体相关性最好,Weibull分布模型和实测数据的拟合性总体要优于Rayleigh分布模型,而Rayleigh分布模型总体要优于对数正态分布模型。
2)通过比较实测数据计算风能密度和由不同分布模型计算风能密度,发现在复杂山地中采用Weibull分布模型计算的结果总体误差最小,年均误差仅为3.24%,对数正态分布模型的年均误差为9.21%,Rayleigh分布模型的年均误差为-22.27%。Weibull分布模型的准确性总体要高于对数正态分布模型和Rayleigh分布模型。
3)研究对象虽然地处内陆复杂山地,但年均风速为5.05 m/s,年均风能密度为173.13 W/m2,风能资源较好,具有较好的风电开发潜力。
综上所述,在风电场建设规划时,预测风速频率分布和风能密度分布应根据实际情况选择拟合性较好和误差较小的分布模型,
才能进行详细分析,并为风电场建设提供更好的资料。
[1]王颖,魏云军.风电场风速及风功率预测方法研究综述[J].西北电力技术,2011,(11):18-21,30.
[2]姚国平,余岳峰,王志征.如东沿海地区风速数据分析及风力发电量计算[J].电力自动化设备,2004,24(4):12-14.
[3]GB/T 18710-2002,风电场风能资源评估方法[S].
[4]孙继良,陈喜军.风能的计算研究[J].1994,20(4):15-19.
[5]王淼,曾利华.风速频率分布模型的研究[J].水力发电学报, 2011,30(6):204-209.
[6]金国骍,胡文忠.风速频率分布混合模型的研究[J].太阳能学报,1994,15(4):353-357.
[7]Atsu S.S.Dorvlo.Estimating wind speed distribution[J].Energy Conversion and Management,2002,(43):2311-2318.
[8]Seguro J V,Lambert T W.Modern estimation of the parameters of the Weibull probability density distribution for wind energy analysis[J].Journal of Wind Engineering and Industrial namics, 2000,(85):75-84.
[9]Jamil M,Parsa S,Majidi M.Wind power statistics and tion of wind energy density[J].Renewable Energy,1995,55(5):405-414.
[10]Garcia A,Torres JL,Prieto E,et al.Fitting probability density distributions:A case study[J].Solar Energy,1998,62(2):139-144.
[11]Hennessey J J.A comparison of the Weibull and Rayleigh distributions for estimating wind power potential[J].Wind neering, 1978,2(3):156-164.
[12]Mathew S,Pandey K P,Kumar A V.Analysis of wind regimes for energy estimation[J].Renewable Energy,2002,(25):381-399.
[13]Kavak A E,Akpinar S.A statistical analysis of wind speed data used in installation of wind energy conversion systems[J].Energy Convers Manage,2005,(46):515-532.
2015-12-14
可再生能源电力技术湖南省重点实验室(长沙理工大学)开放基金(2012ZNDL008);湖南省科技计划项目(2014GK3150)
陈桂宝(1990—),男,硕士研究生,主要从事风能资源评估、风力发电、热工过程检测与智能控制、计算仿真与优化方面的研究。252024357@qq.com

