On n-K Width of Certain Function ClassesDefined by Linear Operators in L2Space
YU Rui-fang,WU Ga-ridi
(Department of Mathematics,Inner Mongolia Normal University,Huhhote 010022,China)
On n-K Width of Certain Function Classes
Defined by Linear Operators in L2Space
YU Rui-fang,WU Ga-ridi
(Department of Mathematics,Inner Mongolia Normal University,Huhhote 010022,China)
Let M(u)be an N-function,Lr(f,x)and Kr(f,x)are Bak operator and Kantorovich operator,WM(Lr(f))and WM(Kr(f))are the Sobolev-Orlicz classes defined by Lr(f,x),Kr(f,x)and M(u).In this paper we give the asymptotic estimates of the n-K widths dn(WM(Lr(f)),L2[0,1])and dn(WM(Kr(f)),L2[0,1]).
linear operator;Sobolev-Orlicz class;width
2000 MR Subject Classification:41A46
Article ID:1002—0462(2016)01—0096—06
Chin.Quart.J.of Math.
2016,31(1):96—101
§1.Introduction and Main Result
Let M(u)be an N-function,that is,
(1)M(u)is an even continuous convex function and M(0)=0;
(2)M(u)>0 for u>0;
Bak operator Lr(f,x)is defined by
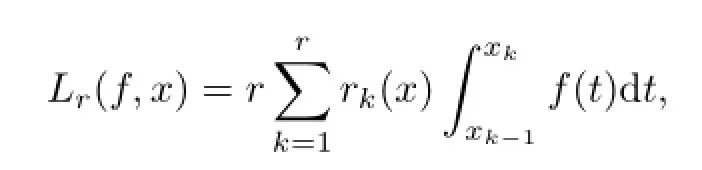
Sobolev-Orlice class WM(Lr(f))is defined by

Kantorovich operator Kr(f,x)is defined by
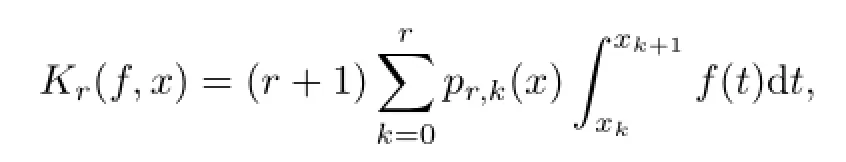
Sobolev-Orlice class WM(Kr(f))is defined by
WM(Kr(f))={f:f(r-1)absolutely continuous on[0,1],and
For any given natural number r,WM(Lr(f))and WM(Kr(f))are two fixed function classes.
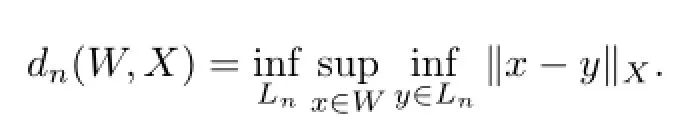
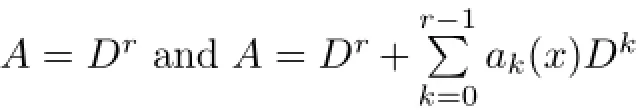
Theorem 1Let M(u)be an N-function satisfying the following conditions,
(1)M(u)is strictly increasing on[0,+∞);
The cases of linear differential operators
(3)M(u)satisfies∆′-condition,this is,M(uv)≤NM(u)M(v)valid for some N>0 and all u,v≥0.
Then
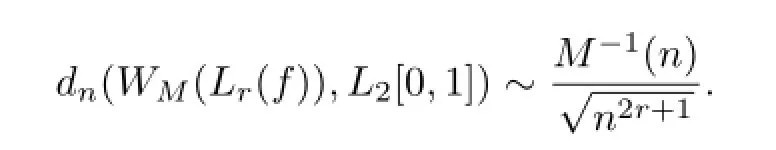
Theorem 2Let M(u)be an N-function satisfying the conditions of Theorem 1,then
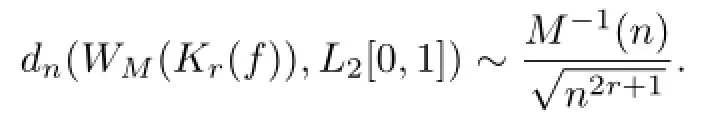
Where the expression an~bnmeans that C1bn≤an≤C2bnfor some C1,C2>0.
§2.Auxiliary Lemmas
Lemma 1[4]Assume{e1,e2,···,ep}is an orthogonal system of vectors in a Hilbert space H and‖ek‖=h,k=1,2,···,p,then
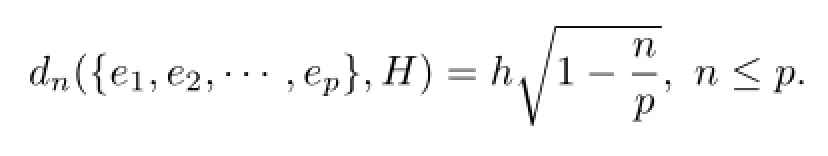
Lemma 2[2]Assume f(x)(x∈[0,+∞))is a monotonically increasing convex function andwhere x(t)is non-negative continuous on[a,b],then

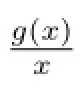

§3.Proof of Theorem
Proof of Theorem 1First of all,let us estimate a lower bound of dn(WM(Lr(f)),L2[0, 1]).We fix an infinitely differentiable function g0(x),such thatfor x∈[0,1]and g0(x)=0 forLet us construct 2n functions
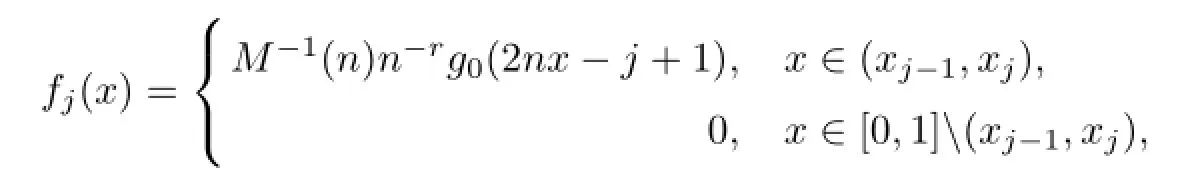
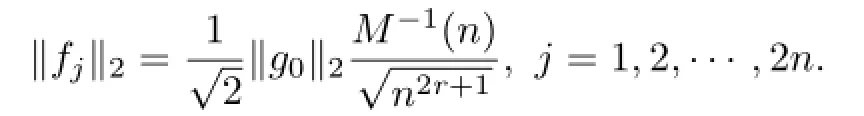
Set
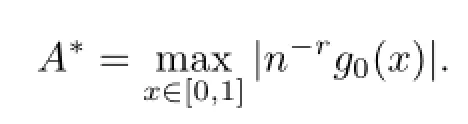
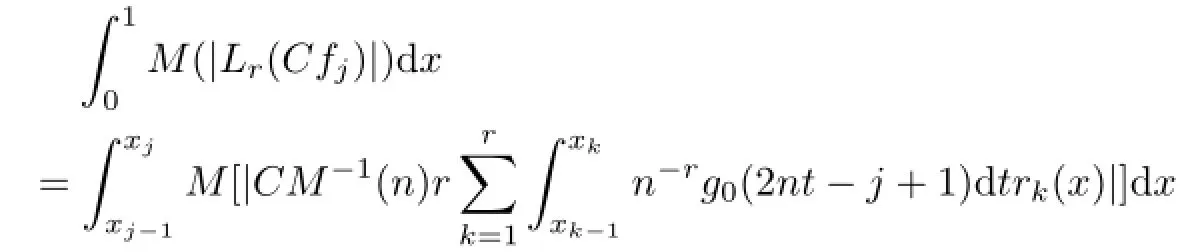

This means that Cfj(x)∈WM(Lr(f)),j=1,2,···,2n,from the Lemma 1,we have

furthermore
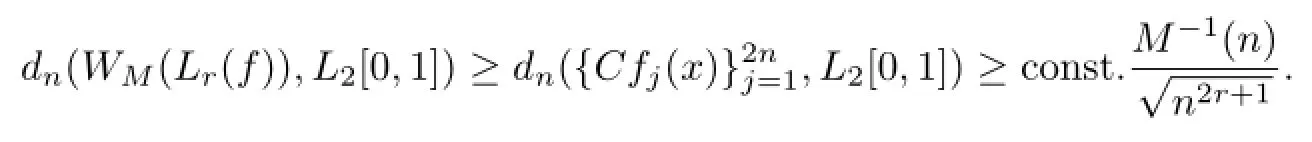
Secondly,we estimate an upper bound of dn(WM(Lr(f)),L2[0,1]).Let us divide interval[0,1]into n equal parts and obtain n subintervals[xj-1,xj),j=0,1,···,n,.For f(x)∈WM(Lr(f)),set

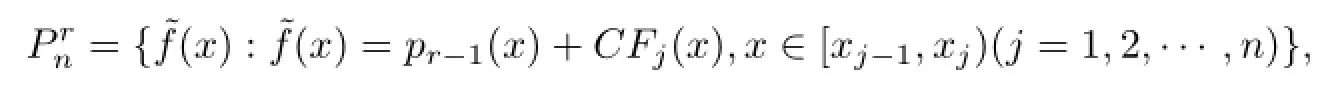
where pr-1(x)is a algebraic polynomial of degree not greater than r-1 and C is any constant. Thenis a linear subspace and dim
For f(x)∈WM(Lr(f)),let us choose a functionthat is
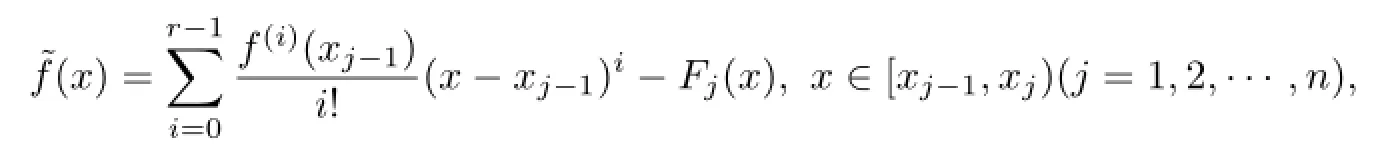
then
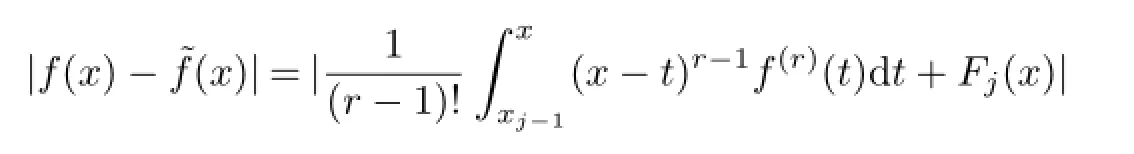
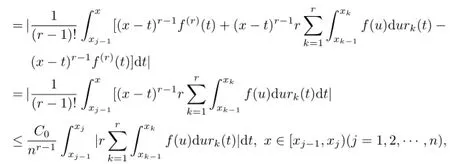
where C0is a constant.
Set
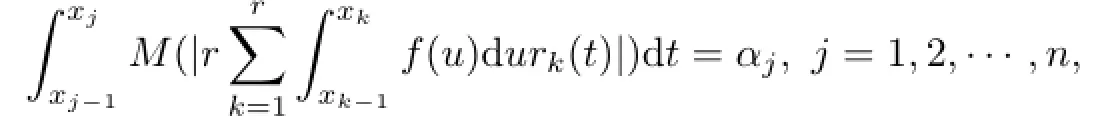

By Lemma 2,we obtain
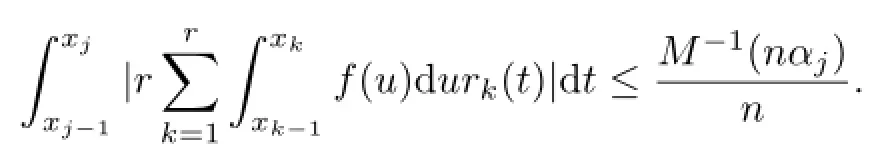
It follows from Lemma 3 and the Condition(2)in Theorem 1 that
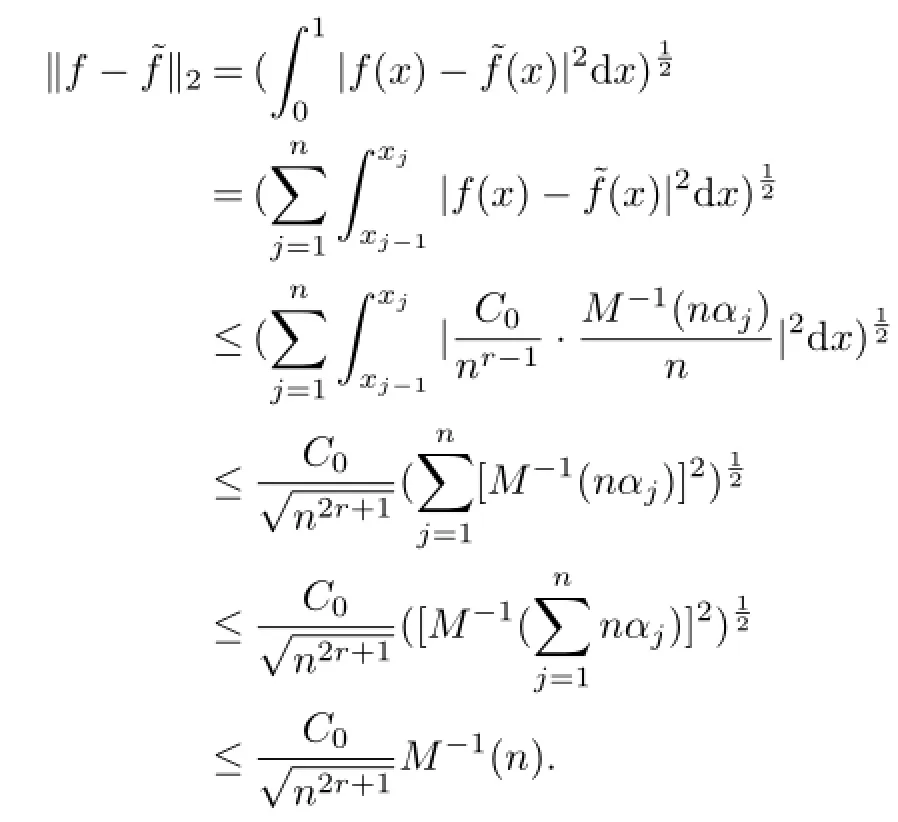
By the definition of Kolmogorov width,we obtain

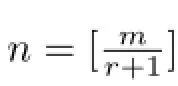

Form this and the monotonicity of M-1(u),we have
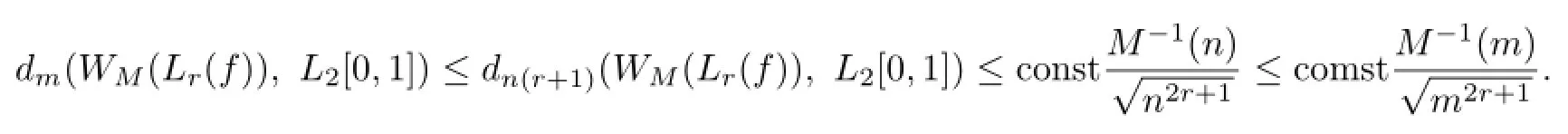
Add it all up,we can obtain
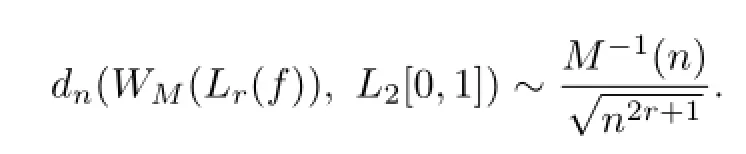
The proof of Theorem 1 is finished.
The proof of Theorem 2 is similar to the proof of Theorem 1,we omit it here.
[References]
[1]WU Cong-xin,WANG Ting-fu.Orlicz Space and Its Applications(in Chinese)[M].HaErBin:Science and Technic of Hei longjiang Press,1983.
[2]ISMAGILOV R S,NASYROVA KH.Diameters of a class of smooth function in the space L2[J].Mat Zametki,1977,(22):671-678;See Also Math Notes,1977,(22):865-870.
[3]WU Ga-ridi,BAO Na.On n-K width certain of function classes defined by linear differential operators in L2space[J].Chinese Quarterly Journal of Mathematics,1999,14(4):27-30.
[4]STECHKIN S B.On the best approximation of given classes of functions by arbitrary polynomials[J].Usp Mat Nauk,1954,(9):133-134.
[5]SUN Yong-sheng.The Theory of Approximation of Function(Vol.1)(in Chinese)[M].Beijing:Beijing Normal University Press,1989.
[6]MAKOVOZ Y.On n-widths of certain functional classes defined by linear differential operators[J].Proc AMS,1983,89(1):109-112.
[7]PINKUS A.n-widths in Approximation Theory[M].Berlin:Springer-Verlag,1985.
O174.41Document code:A
date:2015-06-25
Supported by the National Natural Science Foundation of China(11161033);Supported by the Inner Mongolia Normal University Talent Project Foundation(RCPY-2-2012-K-036);Supported by the Inner Mongolia Normal University Graduate Research Innovation Foundation(CXJJS14053);Supported by the Inner Mongolia Autonomous Region Graduate Research Innovation Foundation(S20141013525)
Biographies:YU Rui-fang(1991-),female(Meng),native of Chifeng,Inner Mongolia,postgraduate,engages in function approximation theory;WU Ga-ridi(1962-),male(Meng),native of Tongliao,Inner Mongolia,Master Instructor,a professors of Inner Mongolia Normal University,engages in function approximation theory.
 Chinese Quarterly Journal of Mathematics2016年1期
Chinese Quarterly Journal of Mathematics2016年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- A Remark on Persistence of Regularity for the Nonlinear Boussinesq System in Dimension Two
- Mixed Finite Element Formats of any Order Based on Bubble Functions forStationary Stokes Problem
- Two Notes on Topological Groups
- Analysis of an Implicit Finite Difference Scheme for Time Fractional Diffusion Equation
- An Efficient Construction of Secure Network Coding
- The Asymptotic Limit for the 3D Boussinesq System
