二沉池一维通量模型的应用及发展*
何志江,张源凯,王洪臣,齐 鲁,尹训飞,张晓军
(中国人民大学环境学院,北京 100872)
二沉池一维通量模型的应用及发展*
何志江,张源凯,王洪臣,齐鲁,尹训飞,张晓军
(中国人民大学环境学院,北京100872)
对基于二沉池一维通量模型进行了综述,介绍了一维通量模型中沉降速率模型在二沉池设计和运行中的应用,对比了不同的污泥沉降性能参数(Sludge Settling Parameters,SSPs)与Vesilind沉降速率模型中参数ν0和a的关系,得出了搅拌条件下的污泥容积指数(SSVI3.5)是最具代表性的污泥沉降性能参数,其能更加全面准确地反映二沉池中活性污泥的性质和状态,SSVI3.5在一维通量模型中的应用使得模型更能接近实际的运行情况,同时指出了一维通量模型在实际应用中仍然存在的缺陷。
二沉池;一维通量模型;沉降速率模型;污泥沉降性能参数
活性污泥法是污水处理中最重要的生物处理方法之一,其中二沉池在处理过程中起到了不可或缺的作用,一方面对污泥混合液进行泥水分离,保证出水中的悬浮物达标排放;另一方面对污泥进行浓缩、回流,保证污水生物处理系统的高效稳定运行[1]。现有的数学模型能够对二沉池的运行过程进行模拟,在二沉池的优化设计和运行控制中具有非常重要的价值。二沉池的模型,已报导的有一维通量模型、二维和三维流场模型以及经验模型,其中二沉池一维通量模型与其他模型相比简单方便的优点更加突出,因此其在理论和应用方面也变得更加成熟[2-3]。近20年来国际上关于二沉池一维通量发表的文章数呈逐年增加的趋势,逐渐成为未来研究的热点,而其沉降速率模型和参数的选择在实际应用中起到了关键性的作用。目前一维通量模型的污泥沉降性能参数大都使用SVI,而很少有研究明确提出模型应用中最佳参数。笔者总结一维通量模型中沉降速率模型在二沉池设计中的应用,对比了不同的污泥沉降性能参数与Vesilind沉降速率模型中参数ν0和a的关系,提出了最具代表性的污泥沉降性能参数,同时指出了一维通量模型在实际应用中存在的缺陷以及未来的发展趋势。
1 一维通量模型
二沉池一维通量模型具有求解简单的特点,可以实现模拟活性污泥的整个沉降过程。一维通量模型主要应用于污水处理系统中二沉池的控制和运行[1]。
常用二沉池的一维通量模型的理论基础是由Kynch(1952)[4]提出的固体通量和Diehl(1995)[5]提出的质量守恒方程,模型的假设条件如下:① 所有悬浮固体颗粒浓度在二沉池的任何一个水平面上完全均匀分布;② 在二沉池中,不考虑生物反应的影响;③进入各个微分体积的物质通量既不能超过该体积所能容纳的物质通量,也不能超过下一个微分体积所能容纳的物质通量;④重力沉降速率只与悬浮物固体浓度有关。
在二沉池的进水口,液体和悬浮颗粒物都均匀分布在水平横截面上,进入二沉池的流量一部分向下流向底部出口,另一部分向上的流量流向顶部的出口。二沉池中固体传输的发生是通过流体相对于边壁的流动和固体相对于水的沉降实现的。总的固体通量(JT)既包括固体重力沉降通量(Js=vsX),也包括因流体流动引起的固体传递通量(JB=qX),即:
JT=Js+JB=vsX+qX(1)
式中:q为流体的垂直方向的速率,m/h;vs为污泥的沉降速率,m/h;X为污泥浓度,kg/m3。
其中q可定义为(如图1所示):

图1基于一维通量的二沉池的流程

式中:Qe为二沉池出水流量m3/h;Qun为二沉池回流量,m3/h;qov为溢流率,m/h;qun为底流率,m/h;A(Z)为水平截面的面积,m2。
其中:

式中:R为回流比;Qf为进水流量,m3/h。所以JB可写为:
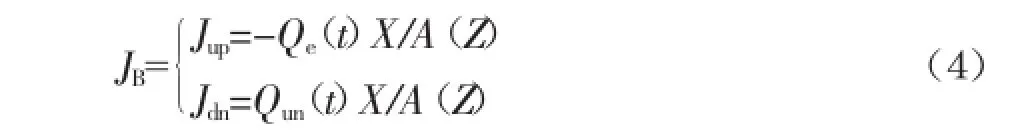
式中:Jup为向上的流动引起的传递通量,kg/(m2·h);Jdn为向下的流动引起的传递通量,kg/(m2·h)。
所以总固体通量JT(X,Z,t)可写为:

式中:Zf为进水层,m;H为二沉池的高度,m。
当Z=H时,JT(X,Z,t)=Jdn,表明二沉池底部不发生污泥颗粒的重力沉降。
将二沉池的垂直方向定义为Z轴,用X(Z,t)来代表在Z高度、t时刻的污泥浓度;A(Z)表示Z高度的截面积;JT表示污泥总固体通量。Z1、Z2表示Z轴上任意的单位体积的边界。则质量守恒定律可表示为:

假设X(Z,t)可微,则该方程是连续的,所以上式可写成:
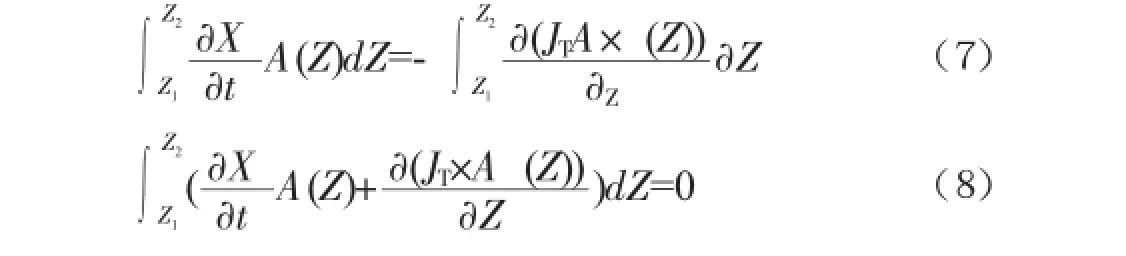
公式(8)对于任意的间隔(Z1、Z2)都适用,假设被积函数是连续的,则有:
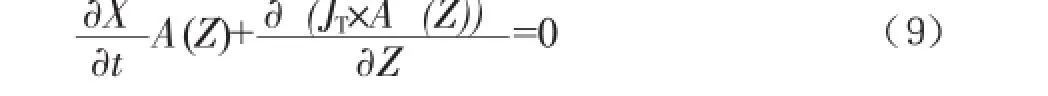
根据上式可以写出一维通量模型的一般形式:

式中:JT(X,Z,t)为总固体通量,kg/(m2·h);S(Z,t)为源项,kg/(m·h);δ为控制函数,数值取1或0。
源项表示单位距离、单位时间进入二沉池的污泥质量,则:
S(Z,t)=Qf(t)Xf(t)/ΔZ(11)
式中:Qf(t)为表示t时刻二沉池进水流量,m3/h;Xf(t)为表示t时刻二沉池的污泥浓度,kg/m3;ΔZ为表示二沉池纵向上的单位距离,m。
2 一维通量中的沉降速率模型
2.1不同沉降速率模型的应用
以二沉池的一维通量模型结构来看,固体通量JT(X,Z,t)是其模型的核心部分,而求取污泥沉降速率是固体通量运用的关键。由于二沉池内发生的沉降现象复杂,一直没有准确的公式来表达污泥的沉降速率。对于二沉池中的主要沉降——区域沉降,通常认为仅与污泥浓度有关,前人的研究中得到了许多不同形式的公式,代表性的研究成果主要有Takács(1991)[6]、Dupont(1992、1995)[7-8]和Otterpohl(1992)[9]等考虑了低污泥浓度污泥的沉降速率以及Härtel(1992)等[10]在模型中考虑了污泥压缩沉降速率。Wett(2002)[11]按二沉池的3种主要沉淀形式(絮凝沉降、区域沉降和压缩沉降),直接建立了1个3层的模型。基于质量守恒定律,对一维通量模型进行了研究。众多国外学者通过实验得到的活性污泥沉降速率模型如表1所示。

表1 活性污泥沉降速率模型
在表1中,指数模型(Vesilind沉降速率模型)由于其简单准确在实际中得到广泛应用。指数模型为:
Vs=V0e-aX(12)
式中:V0为指数模型参数,m/h;a为指数模型参数,L/g。
模型中的参数可通过静态污泥沉降试验测得,也可通过污泥沉降性能指标(SVI、DSVI(diluted SV)I、SSVI(stirred SVI))的经验关系计算得到。
2.2Vesilind沉降速率模型
基于模型应用的实际需求,Cho等[16]认为模型的参数最好不超过2个,综合考虑模型的应用价值和模拟精度,Vesilind沉降速率模型被认为是一个最佳的选择。近年来,国外的学者致力于研究Vesilind沉降速率模型参数ν0和a与常规测定的污泥体积指数SVI之间的相关关系。虽然许多学者对此有很多不同的看法,但是研究结果与实测数据有很强的相关性[23-24],因此得到了广泛使用。选取Vesilind沉降速率模型同时有以下几点原因:①WRc(Water Research Centre)的设计规范是以其为基础;②Rachwal(1982)等[25]用大规模水厂的大量数据对多种沉降速率模型进行拟合,结果表明Vesilind沉降速率模型的相关性要优于其他的沉降速率模型;③Smollen和Ekama(1984)等[26]研究表明,Vesilind沉降速率模型能较好地描述对沉降通量曲线(当X>1 g/L),并且其与多年的水厂的实测数据有较好的相关关系(R2>0.96)。
Vanderhasselt和Vanrolleghem(2000)[27]研究表明Vesilind沉降速率模型能较好地描述沉降速率与污泥浓度之间的关系。Vesilind沉降速率模型的参数可以直接通过活性污泥的静态沉降实验得到,也可以通过它们和污泥沉降性能参数(SSPs)的经验关系式得到;SSPs主要指SVI(Sludge Volume Index)、DSVI(Diluted SVI) 以及SSVI(Stirred SVI)。
2.3Vesilind模型参数v0和a的确定
国外许多学者提出建立污泥沉降性能参数SSPs与沉降速率模型参数v0、a之间的经验关系式,通过测定SSPs来近似地确定v0和a[28-30]。许多研究人员提出了利用SSPs估计v0和a的方法,如表2所示。

表2 SSPs与Vesilind沉降速率模型参数的关系
Ozinsky和Ekama(1995)[24]的研究已表明,SVI的缺点就是其与区域沉降速率没有较好的相关性。出现这种现象的原因可能是SVI和区域沉降速率的测量方式不一致。区域沉降速率是在动态搅拌的情况下测定的,而SVI是在静态的条件下测定的[41]。Daigger(1995)[28]以及Ozinsky(1995)[24]基于大量统计分析均表明SSVI3.5是最佳选择。一般SSVI3.5的测定方法是,在高度与直径比5∶1~6∶1的圆形沉降柱中,以1 r/min搅拌的条件下,测出1~6 g/L不同污泥浓度的SSVI,然后使用插值法来确定在浓度为3.5 g/L时的SSVI,即SSVI3.5,White等[42-43]在1975、1976年提出SSVI3.5有以下几个优点:①能够减少边壁效应、短流和架桥作用的影响;②相同或沉降性能相似的污泥,浓度小于10 g/L且具有良好沉降性能的污泥和浓度小于7 g/L且沉降性能较差的污泥测得的SSVI3.5具有较好的重现性;③3.5 g/L是现有污水处理厂的污泥混合液的平均浓度,因此SSVI3.5具有较高的普适性;④相比SVI和DSVI,SSVI3.5更可靠,因为SSVI3.5是由大量数据统计所得,计算结果的可靠性更高;⑤采用SSVI3.5作为日常测定的沉降参数,将为水厂运行人员和设计工程师提供更准确可靠的沉降性能数据。
3 结论
二沉池一维通量模型的发展及沉降速率模型的应用,得到了SSVI3.5是一个最精确的污泥沉降性能参数,选择其作为联系Vesilind沉降速率模型参数的关键指标,将会使得一维通量模型在应用中变得既简单又准确。但是由于模型本身的缺陷,至今仍不能准确地实现对二沉池出水中悬浮固体浓度的模拟,因此一维通量模型需要在2个方面进行改进:①二沉池内发生的所有沉降现象不能在现有模型中得到精确的表达。在模型中,大部分的沉降速率直接应用区域沉降速率公式,往往忽略了过渡沉降阶段,因此其准确性和科学性还有待进一步研究。②一维通量模型一般不考虑生物反应。但是Henze(1993)[44]认为二沉池发生的反硝化现象较为显著,随后Siegrist(1995)[45]提出了一个描述二沉池中反硝化现象的模型,但是其准确性还有待考究,特别是对于现有的一些模型参数,还需要污水处理厂的大量现场运行数据来校准验证。
[1] 严晨敏,张代钧,卢培利,等.沉淀池模型的研究现状与展望[J].重庆大学学报:自然科学版,2004,27(3):130-133.
[2] Krebs P.Success and shortcomings of clarifier modelling[J].Water Sci Technol,1995,31(2):181-191.
[3] Ekama G A,Marais P.Assessing the applicability of the 1D flux theory to full-scale secondary settling tank design with a 2D hydrodynamic mode[lJ].Water Res,2004,38(3):495-506.
[4] Kynch G J.A theory of sedimentation[J].Tran Faraday Society,1952,48:166-176.
[5] Diehl S.Conservation laws with application to continuous sedimentation[M].Lund University,Lund Institute of Technology,Department of Mathematics,1995.
[6] TakácsI,PatryGG,NolascoD.Adynamicmodeloftheclarificationthickening process[J].Water Res,1991,25(10):1263-1271.
[7] Dupont R,Henze M.Modelling of the secondary clarifier combined with the activated sludge model no.1[J].Water Sci Technol,1992,25(6):285-300.
[8] DupontR,DahlC.Aone-dimensionalmodelforasecondarysettling tank including density current and short-circuiting[J].Water Sci Technol,1995,31(2):215-224.
[9] Otterpohl R,Freund M.Dynamic models for clarifiers of activated sludge plants with dry and wet weather flows[J].Water Sci Technol,1992,26(5/6):1391-1400.
[10] Härtel L,Pöpel H J.A dynamic secondary clarifier model including processes of sludge thickening[J].Water Sci Technol,1992,25(6):267-284.
[11] Wett B.A straight interpretation of solids flux theory for 3-layer sedimentation model[J].Water Res,2002,36:2949-2958.
[12] KalinskeA.Settlingcharacteristicsofsuspensionsinwatertreatment processes[J].J Am Water Works Ass,1948,40(2):113-130.
[13]Yoshioka N,Hotta Y,Tanaka S,et al.Continuous thickening of homogeneous flocculated slurries[J].Chem Eng Tokyo,1957,21:6674.
[14] Thomas D G.Transport characteristics of suspensions relation of hindered settling floc characteristics to rheological parameters[J]. Am Inst Chem Eng J,1963,9:310-316.
[15]Vesilind P A.Theoretical considerations:Design of prototype thickeners from batch settling tests[J].Water Sew Work,1968,115(7):302-307.
[16]Cho S H,Colin F,Sardin M,et al.Settling velocity model of activated sludge[J].Water Res,1993,27(7):1237-1242.
[17] Richardson J F,Zaki W N.The sedimentation of a suspension of uniform spheres under conditions of viscous flow[J].Chem Eng Sci,1954,3(2):65-73.
[18] Scott K J.Mathematical models of mechanism of thickening[J]. Ind Eng Chem Fundam,1966,5(1):109-113.
[19]Scott K J.Theory of thickening:Factors affecting settling rate of solids in flocculated pulps[J].Trans Inst Min Met,1968,77:85-97.
[20] Steinour H H.Rate of sedimentation nonflocculated suspensions of uniform spheres[J].Ind Eng Chem,1944,36(7):618-624.
[21] ShannonPT,StroupeE,ToryEM.Batchandcontinuousthickening. Basic theory.Solids flux for rigid spheres[J].Ind Eng Chem Fundam,1963,2(3):203-211.
[22]Vaerenbergh E V.Numerical computation of secondary settler area using batch settling data[J].Trib Cebedeau,1980,33:369-374.
[23] Ekama G A,Barnard G L,Gunthert F W,et al.Secondary settling tanks[M].London:International Association on Water Quality,1997.
[24] Ozinsky A E,Ekama G A.Secondary settling tank modelling and design.Part 1:Review of theoretical and practical developments[J].Water S A,1995,21(4):325-332.
[25] RachwalAJ,JohnstoneDWM,HanburyMJ,etal.The application of settleability tests for the control of activated sludge plants[J]. Bulking of Activated Sludge,1982:224-242.
[26]Smollen M A,Ekama G A.Comparison of empirical settlingvelocity equations in flux theory for secondary settling tanks[J]. Water S A,1984,10(4):175-184.
[27]VanderhasseltA,VanrolleghemPA.Estimationofsludge sedimentation parameters from single batch settling curves[J]. Water Res,2000,34(2):395-406.
[28] Daigger G T.Development of refined clarifier operating diagrams using an updated settling characteristics database[J].Water Environ Res,1995,67(1):95-100.
[29] Ozinsky A E,Ekama G A.Secondary settling tank modelling and design Part 2:Linking sludge settleability measures[J].Water S A,1995,21(4):333-349.
[30]Giokas D L,Daigger G T,Sperling M,et al.Comparison and evaluation of empirical zonesettling velocity parameters based on sludgevolumeindexusing a unified settling characteristics database[J].WaterRes,2003,37(16):3821-3836.
[31] Forster C F.A further examination of mass flux theory as applied to activated sludge settlement[J].Biotechnol Lett,1982,4(6):381-386.
[32] DaiggerGT,RoperJrRE.TherelationshipbetweenSVIandactivated sludge settling characteristics[J].J Water Pollut Contr Federat,1985,57(8):859-866.
[33]Pitman A R.Settling of nutrient removal activated sludges[J]. Water Sci Technol,1984,17(4/5):493-504.
[34] Wahlberg E J,Keinath T M.Development of settling flux curves usingSVI:Anaddendum[J].WaterEnvironRes,1995,67(5):872-874.
[35] 黄勇,幸响付.SVI与固体通量模型参数的相关性研究[J].苏州城建环保学院学报,1992(2):1-7.
[36]Akca L,Kinaci C,Karpuzcu M.A model for optimum design of activated sludge plants[J].Water Res,1993,27(9):1461-1468.
[37] MinesJrRO,VilagosJL,EchelbergerJrWF,etal.Conventional and AWT mixed-liquor settling characteristics[J].J Environ Eng,2001,127(3):249-258.
[38] TuntoolavestM,GradyJrCPL.Effectofactivatedsludgeoperational conditions on sludge thickening characteristics[J].J Water Pollut Contr Federat,1982:1112-1117.
[39]Koopman B,Cadee K.Prediction of thickening capacity using diluted sludge volume index[J].Water Res,1983,17(10):1427-1431.
[40]Von Sperling M,Fróes C V.Determination of the required surface area for activated sludge final clarifiers based on a unified database[J].Water Res,1999,33(8):1884-1894.
[41] Gilcreas F W.Standard methods for the examination of water and waste water[J].Amer J Public Health,1966,56(3):387-388.
[42]White M J D.Settling of activated sludge[M].England:Water Research Centre,1975.
[43] White M J D.Design and control of secondary settling tanks[J]. Water Pollut Con,1976,75(4):459-467.
[44]Henze M,Dupont R,Grau P,et al.Rising sludge in secondary settlers due to denitrification[J].Water Res,1993,27(2):231-236.
[45] Siegrist H,Krebs P,Bühler R,et al.Denitrification in secondary clarifiers[J].Water Sci Technol,1995,31(2):205-214.
Application and Development of One-dimensional Flux Model for Secondary Settling Tank
He Zhijiang,Zhang Yuankai,Wang Hongchen,Qi Lu,Yin Xunfei,Zhang Xiaojun
(School of Environment and Natural Resources,Renmin University of China,Beijing 100872)
One-dimensional flux model of secondary settling tank was reviewed,and the application of settling velocity model ofone-dimensional flux model in the design and operation of secondary settling tank wasintroduced.In addition,the relationships between the different sludge settling parameters(SSPs)and v0,a in Vesilind settling velocity model were compared. The stirred sludge volume index(SSVI3.5)wasthe most representative sludge settling parameter because it can reflect the propertiesof activated sludge more comprehensive and accurately in secondary settling tank,and itsapplication in one-dimensional flux model wasmore close to the actual running situation.Meanwhile,the drawbacksof one-dimensional flux model in practical application were pointed out.
secondary settling tank;one-dimensional flux model;settling velocity model;sludge settling parameters
X703.1
A
1005-8206(2016)04-0072-05
国家高技术研究发展计划(863计划)项目(2012AA063404);城市污水处理厂节能降耗稳定运行技术集成研究与示范项目(2013ZX071314-001)
2015-02-04
何志江(1991—),在读硕士研究生,主要从事水污染控制治理研究.
E-mail:18046043293@163.com

