多成本和绿色飞行的机队规划

谷润平，李佳妮，魏志强，褚双磊

(1.中国民航大学 空中交通管理学院，天津 300300；2.天津市空管运行规划与安全技术重点实验室，天津 300300)



多成本和绿色飞行的机队规划

谷润平1,2，李佳妮1，魏志强1,2，褚双磊1,2

(1.中国民航大学 空中交通管理学院，天津 300300；2.天津市空管运行规划与安全技术重点实验室，天津 300300)

为了减少航空公司的运营成本，以燃油成本最小、时间成本最小、碳排放成本最小以及机型利用率最平均为目标函数，建立了多目标整数优化模型。以某航空公司的实际数据为算例，代入优化模型确定最优机队配置。对各子目标的权重进行灵敏度分析，得到了不同权重组合对总运营成本和碳排放量的影响，给出可选的权重范围。研究结果表明：本文的优化模型一年可以为该航空公司节省约2 869万元运营成本，少排放 7 665 t CO2。

机队规划；多目标规划；绿色飞行；层次分析法；灵敏度分析

0　引言

近年来，中国航空业不断发展，航空公司间的竞争愈加激烈，如何对机队现有机型进行合理有效的配置一直是各航空公司关注的焦点[1]。燃油成本占直接运营成本的比重相对较大[2]，时间成本能够直接反映出不同机型每小时飞行所产生的成本[3]。欧盟在2005年和2008年分别通过了“温室气体排放权交易机制”和“碳排放配额交易体系”[4]，绿色飞行已成为今后航空飞行的必然选择。

文献[5]在满足旅客需求波动规律的前提下，将航线上的时段分割成时间区间，针对每个时间区间，构造以利润最大化为目标函数的整数规划模型，此模型能够反映出航空公司模拟运营环境的相关特点。文献[6]分析得出影响航空公司运营的关键因素是供需关系，通过相关机队构成、机队规模以及机型选择3个步骤建立机队规划鲁棒性模型。文献[7]基于鲁棒性建立了以航线网络运力利润最大化为目标的分配方案。文献[8]运用动态规划方法,以收益最大化为目标函数,建立了考虑超售策略的航班动态舱位分配控制模型,通过对模型的性质分析,证明了模型存在最优解。

以上研究都没有将航空公司最重视的运营成本与近几年备受关注的碳排放联系起来考虑，只是从某一方面对现有机队进行规划。基于此，本文将燃油成本最小、时间成本最小以及碳排放成本最小作为目标函数，同时针对优化后的机型利用率不平均的特点，在目标函数中又引入了不同机型利用率与机队现有机型平均利用率之差的和最小，从经济性、环保性和平均机型利用率3个方面对航空公司的机队进行规划。对所选的各子目标权重进行灵敏度分析，并分析了不同权重组合下总运营成本的变化趋势。同时，针对近年来全球化绿色飞行的要求，给出了不同权重组合下碳排放量的变化趋势以及子目标的权重范围，验证了算法的有效性。

1　机队优化配置模型

1.1目标函数

假设某航空公司现有机队拥有m种机型，n条航线，每天第i种机型(i=1,2,…,m)在第j条航线(j=1,2,…,n)上的航班数量为xij，建立优化目标函数为：

(1)

其中：f1(x)为每天航班飞行任务产生的最小燃油成本；f2(x)为每天航班飞行任务产生的最小时间成本；f3(x)为每天航班飞行任务产生的最小碳排放成本；f4(x)为每天航班飞行任务中不同机型利用率与机队现有机型平均利用率之差的和最小，即机型利用率最平均；WFi为第i种机型的燃油流量，t/h；tij为第i种机型在第j条航线上平均执行一次航班飞行所用时间，h；PF为当年燃油价格，元/t；PCi为第i种机型平均执行一次航班飞行所产生的时间成本，元/h；PC为当年碳排放的单价，元/t；η为碳排放因数；Ti为第i种机型的日飞行总时间，h。

1.2约束条件

(Ⅰ)现有机队飞行频率限制：

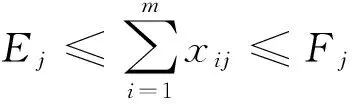
(2)

其中：Ej和Fj分别为航线j每天的最小航班频率和最大航班频率。本项约束条件受市场运输需求、航班飞行时间、政治和地区等因素限制。

(Ⅱ)客运量限制：

(3)

其中：NSi为机型i的座位数；ri为机型i的客座率；REj为航线j的最大客运量。每条航线上执行飞行任务，选择机型所提供的座位数不得小于此航线的最大客运量。

(Ⅲ)飞机飞行寿命限制：

(4)

不同机型因性能要求，每天的总飞行时间受到限制。

(Ⅳ)连续航班限制：

xij=xij(i=1,2,…,m;j=1,2,…,n)。

(5)

考虑到实际数据中会有连续航班的要求。

(Ⅴ)其他因素限制：

xij≥0且为整数，

(6)

其中：xij>0表示机型i可以在航线j上飞行；xij=0表示机型i不可在航线j上飞行；xij的取值只能是不小于0的正整数。

1.3模型算法

层次分析法(analytic hierarchy process，AHP)是一种系统分析方法，适用于结构较复杂、决策准则较多且不易量化的决策问题[9]。层次分析法的基本内容：首先，根据问题的性质和要求，提出一个总目标；然后，将问题按层次分解，对同一层内的诸因素通过两两比较的方法确定相对于上一层目标的各自权系数。这样层层分析下去，直到最后一层，即可给出所有因素(或方案)相对于总目标按重要性(或偏好)程度的一个排序，得到新目标函数：

minf(x)=ω1f1(x)+ω2f2(x)+ω3f3(x)+ω4f4(x)。

(7)

为了统一不同子目标的数量级，使模型具有实用性，进一步做归一化处理，可得最终的优化模型：

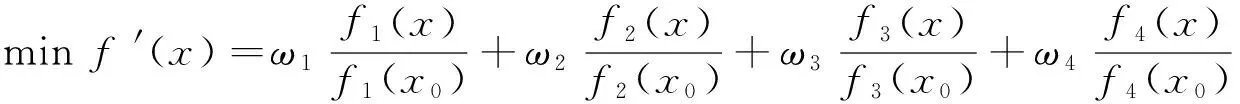
(8)

(9)

本文使用专家法[3]来确定不同子目标的权重系数ω，根据对不同航空公司相关部门的走访，可知燃油成本所占权重为ω1=0.48;时间成本所占权重为ω2=0.24;碳排放成本所占权重为ω3=0.18。根据总权重系数为1可知：不同机型的利用率所占权重为ω4=0.10。

1.4算例应用

1.4.1已知数据

已知某航空公司现有4种机队机型，各机型的相关性能数据如表1所示。该公司运营的40条航线，相关数据如表2所示。

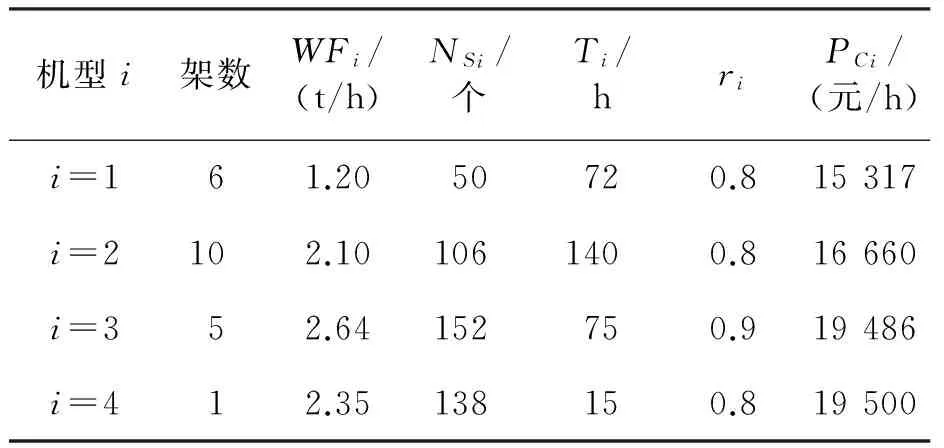
表1　机型相关性能数据

表2　航线相关数据

根据该航空公司的实际数据，有连续航班限制要求xi17=xi18，xi22=xi23，xi32=xi33，xi34=xi35=xi36；航线适航性航程限制要求x101=x102=x103=x107=x207=0；机场适航性最大起降高度限制要求x240=x340=0；航线适航性飘降与供氧问题限制要求x140=x240=x340=0。对于表2中tij表示为“-”的情况，在计算时取tij=0。

表3　机队原航班配置方案

机队原航班配置方案如表3所示。燃油价格为 7 200 元/t[10]；根据欧盟规定[11]：碳排放的单价为150元/t；碳排放因数取3.115。由此计算，机队原配置方案每天产生的燃油成本f1(x0)为 3 835 245.6元；时间成本f2(x0)为4 296 444.5元；碳排放成本f3(x0)为 248 891.5元；3种机型的飞机利用率与平均利用率的差之和f4(x0)为0.758 9;碳排放量为1 659.3 t。

1.4.2优化后方案

由所建的优化模型(8)，代入相应的数据可得优化后每天的燃油成本f1(x)为3 786 818.4元；时间成本f2(x)为4 269 408.2元；碳排放成本f3(x)为 245 748.7元；3种机型的飞机利用率与平均利用率的差之和f4(x)为0.745 4；碳排放量为1 638.3 t。最优机队机型配置方案如表4所示。

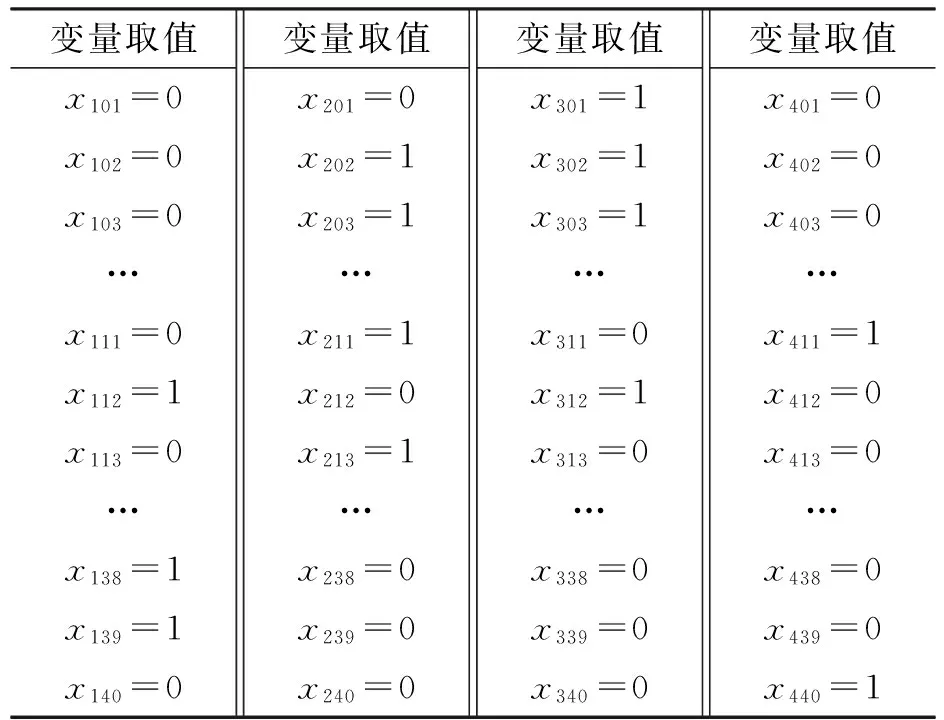
表4　最优机队机型配置方案

1.4.3最优方案分析

对比表3和表4可知：新的机队机型配置方案相较于原方案，成本降低了78 606.3元/d，节约率约为0.9%；碳排放量降低了21 t/d，节约率约为1.3%；各机型飞机利用率之和提高约1.8%。对于长期运营来说，一年可以为该航空公司节省约2 869万元运营成本，少排放7 665 t CO2，在经济性和环保性方面具有显著的效果。

2　权重灵敏度分析

由于所在地区情况不同，在实际运营中各航空公司对不同成本的权重会有所不同。本文使用MATLAB进行编程，得到不同权重下产生的相关成本变化趋势图，即对各子目标的权重进行灵敏度分析。考虑到现有机队飞机利用率平均化这个目标函数并不是成本，故将ω4恒置为0.1。

2.1燃油成本、时间成本和碳排放成本的不同权重对总成本的影响

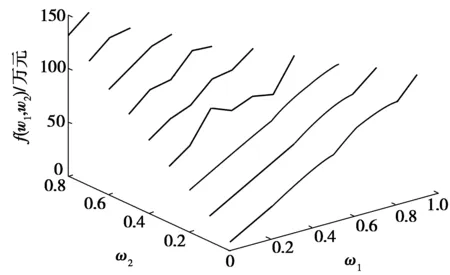
图1　不同 ω1和 ω2对总成本f(x)的影响

利用三维立体图可以同时分析多个成本的变化对总成本的影响：ω1、ω2在一定范围内取值,根据ω1+ω2+ω3+ω4=1可以得到ω3。分析不同的(ω1,ω2,ω3)组合对总成本f(x)的影响，再利用MATLAB进行编程，得到的结果如图1所示。

由图1可以看出：在ω4确定的情况下，不同燃油成本权重ω1和时间成本权重ω2对总成本f(x)有影响。通过分析可以知道：ω1取值0～0.6、ω2取值 0～0.6时，总成本相对较低，且在上述变化范围内，当ω1取值越大、ω2取值越小时，总成本越小。

2.2燃油成本、时间成本和碳排放成本的不同权重对碳排放成本的影响

分析不同的(ω1,ω2,ω3)组合对碳排放成本f3(x)的影响，再利用MATLAB进行编程，得到的结果如图2所示。

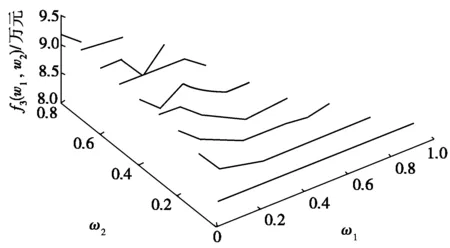
图2　不同 ω1和 ω2对碳排放成本f3(x)的影响

由图2可以看出：当时间成本权重ω2取值0～0.4时，碳排放成本在一个较低的水平，则碳排放量也在一个相对较低的水平；随着ω2的继续增大和ω1的逐渐减小，碳排放成本会变大，则碳排量也会变大。

2.3结果分析

由图1与图2可知：当ω4=0.1、ω1取值0～0.6、ω2取值0～0.4、ω3取值0～0.4时，得到的总成本和碳排放量相对较少，可以达到优化航空公司总运营成本的目的。本文所取权重就在这个范围内，说明本文的算例及计算结果可信度高，算法有效。

3　结束语

本文建立了以燃油成本最低、时间成本最低、碳排放成本最低以及飞机利用率最平均的机队规划多目标整数模型，采用层次分析法对模型进行求解。对不同子目标权重进行了灵敏度分析，给出不同权重组合下总运营成本和碳排放量的变化趋势，达到降低燃油成本、时间成本和碳排放量的目的。同时使机队现有机型的利用率平均化，并给出了不同权重的有效取值范围，验证了优化结果和算法的可靠性。

[1]TEOH L E,KHOO H L.Green air transport system:an overview of issues,strategies and challenges[J].KSCE journal of civil engineering,2016,20(3):1040-1052.

[2]谷润平,陈慧,王鹏.基于燃油成本最小的机队规划研究[J].航空计算技术,2013，43(4):6-8.

[3]谷润平,王倩.基于成本控制的机队优化配置方法[J].航空计算技术,2014,44(3):19-22.

[4]MC C D.Climate policy and the airline industry:emissions trading and renewable jet fuel[D].Cape Town:Massachusetts Institute of Technology,2012.

[5]汪瑜,孙宏,朱金福.基于时间区间内航线机型优化分配的机队规划方法[J].系统工程理论与实践,2015,35(1):168-174.

[7]孙宏,张培文,汪瑜.基于航线网络运力优化分配的机队规划方法[J].西南交通大学报,2010,45(1):111-115.

[8]乐美龙,张健泽.航班超售与舱位控制综合优化[J].河南科技大学学报(自然科学版),2013,34(3)：25-29.

[9]邓雪,李家铭,曾浩健,等.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,42(7):93-100.

[10]柴建,张钟毓,李新,等.中国航空燃油消费分析及预测[J].管理评论,2016,28(1):11-21,41.

[11]魏志强,刁华智,韩博.民用飞机巡航阶段污染物排放量计算研究[J].科学技术与工程,2014(19):122-127.

国家“863”计划基金项目(2014AA110501);国家自然科学基金项目(U1533116,21407174);工业和信息化部航空科学基金项目(20140267002)

谷润平(1971-),男,陕西榆林人,副教授,硕士，主要研究方向为飞机性能和飞行力学.

2016-04-06

1672-6871(2016)06-0037-05

10.15926/j.cnki.issn1672-6871.2016.06.008

U8

A