基于惯性系的光纤寻北仪双位置寻北算法

蒋　杰，黄　茗，杨功流，史　俊，周　潇

（1.北京航空航天大学仪器与光电工程学院，北京100191；2.中船工业集团九江精密测试技术研究所，九江332000）

基于惯性系的光纤寻北仪双位置寻北算法

蒋杰1，黄茗2，杨功流1，史俊1，周潇1

（1.北京航空航天大学仪器与光电工程学院，北京100191；2.中船工业集团九江精密测试技术研究所，九江332000）

由低精度光纤陀螺（Fiber Optical Gyroscope，FOG）组成的寻北仪具有结构简单、成本低的优点，但易受地磁和车上复杂外部环境的影响。针对低精度FOG存在地磁零位，寻北仪对外部晃动敏感的缺陷，通过对陀螺进行地磁零位补偿保证陀螺零偏稳定性，在此基础上提出了基于惯性系的双位置寻北算法。算法分别在两个对位进行惯性系寻北，利用双位置对消原理获得不受陀螺固定零偏影响的方位角并完成水平陀螺固定零偏的估计。实验结果表明，陀螺零偏稳定性0.15（°）/h，加速度计零偏稳定性150μg的惯性器件精度下，车上寻北误差1倍标准差小于4.5mil、极差小于10mil、对准时间小于5min。与传统双位置算法相比，所提算法在晃动基座条件下具有对准精度高，环境适应性强的优点。

低精度FOG；地磁零位补偿；惯性系双位置寻北；晃动基座

0　前言

车载光纤寻北仪是一种给车上光电探测头提供姿态及方位信息的设备，并且具有短时间方位保持功能。寻北仪的寻北精度由组成寻北仪的惯性器件及寻北方案决定。传统寻北仪有二位置、三位置、四位置、多位置以及动态寻北等应用方案［1-3］。相对三位置、四位置、多位置以及动态寻北方案，二位置寻北方案具有寻北时间短、计算简单等优点，因此常在工程上使用。

二位置寻北方案是将光纤陀螺垂直放在转位机构的平台上，转位机构旋转得到陀螺与加速度计处在两个不同位置下的输出。通过计算寻北仪两水平加速度计输出得到水平姿态角。利用两个不同位置的陀螺输出数据的平均值相减得到地速北向分量在航向上的投影从而获取航向角信息。二位置寻北方案提高寻北精度的关键在于双位置对消思想的应用。双位置对消要求陀螺不同方位的零位保持稳定，但是低精度FOG会在地磁的作用下产生地磁零位［4-6］。传统寻北算法主要使用一个陀螺的数据，由于陀螺输出数据中地速信息的信噪比与陀螺所处的方位相关，算法精度受初始方位的影响［7］。算法中航向信息是通过计算两个位置的陀螺输出平均值获取，因此晃动基座条件下寻北误差增大，甚至不能正常寻北。惯性系寻北算法通过观察一段时间内重力矢量在惯性空间中转动形成的锥面获取不受界干扰角速度影响的地球自转角速度信息，据此解算出寻北仪的水平姿态和方位信息［8］。惯性系寻北算法能保证晃动条件下的寻北精度且与初始方位没有关系，但无法克服由陀螺固定零位带来的寻北误差。

车载寻北仪需克服车体晃动及高空阵风对寻北精度的影响，对寻北方案及陀螺误差补偿技术提出了新的要求。针对传统算法的缺点，同时也为了适应新一代寻北仪中体积小、重量轻但内部电磁环境复杂的特点，本文提出了一种具有双位置及惯性系寻北优点的双位置寻北算法。

1　基于惯性系双位置寻北算法的研究

惯性系寻北算法是单位置寻北算法，虽然能克服外界干扰角速度对寻北精度的影响，但无法消除陀螺固定零偏对寻北精度的影响。传统双位置算法能通过对消去掉固定零偏的影响，但不能克服外界干扰角速度。新的算法在对陀螺进行地磁零位补偿的基础上，同时引入两种算法提高精度的思想，从原理上综合了两种算法的优点。

1.1地磁零位的补偿

光纤陀螺是利用Sagnac效应工作的惯性器件［9］。由于光纤环易受地磁的影响，当光纤环的敏感轴向朝向不同时，由于光纤环的磁通量发生变化，导致陀螺零位发生变化。光纤陀螺的法拉第效应表明，磁场对光纤陀螺的影响是线性的且与磁场大小成正比。任意方向磁场对光纤陀螺的作用都可以分解为正交两磁场单独作用之和。当光纤环恒定不变时，正反两束光产生的相位差不变，陀螺的零偏不发生变化。当磁场的方向与强度变化时，法拉第效应会引起陀螺的附加漂移。光纤陀螺磁场方向满足θ0=-δ±π时，磁场对光纤陀螺的相位影响最大，此时地磁零位变化最大。法拉第效应的大小与光纤环的半径及圈数有着密切的关系。由于同一地点地磁场恒定不变，因此地磁引起的零位变化在同一方位是一个定值。在地磁的影响下，光纤陀螺的零位随方位的变化呈近似正弦变化［6］。提高双位置寻北精度，需对组成的寻北仪的低精度FOG地磁零位进行补偿。

1.2惯性系双位置寻北的原理

单位置寻北条件下，寻北仪的水平姿态及航向误差是由陀螺及加速度计的零位决定。其中加速度计零位决定水平姿态的极限误差，等效东向陀螺漂移决定方位角的极限误差。惯性系的双位置对准算法是指在两个相差180°的对位分别进行惯性系寻北算法，得到系统在两个对位的三个姿态角。水平角近似为0的条件下，由于陀螺短时间内零位的变化小，处在两个对位的寻北仪的等效东向零偏之和约为0。因此可根据对消原理处理两个位置的寻北结果，去掉陀螺固定零偏带来的方位失准角的影响，提高寻北的精度。

单位置进行寻北时，寻北仪的水平姿态和方位姿态精度由极限精度公式［10］决定。

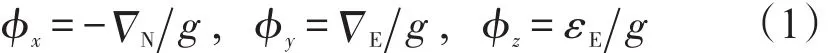
双位置对准算法中，第一个位置的等效陀螺

与加计零偏如式（2）所示。

第二个位置的等效陀螺与加计零偏如式（4）、式（5）所示。

当水平姿态近似为0，两位置相差180°时，θ≈0°、γ≈0°、φ≈180°，式（4）、式（5）可以简化为：

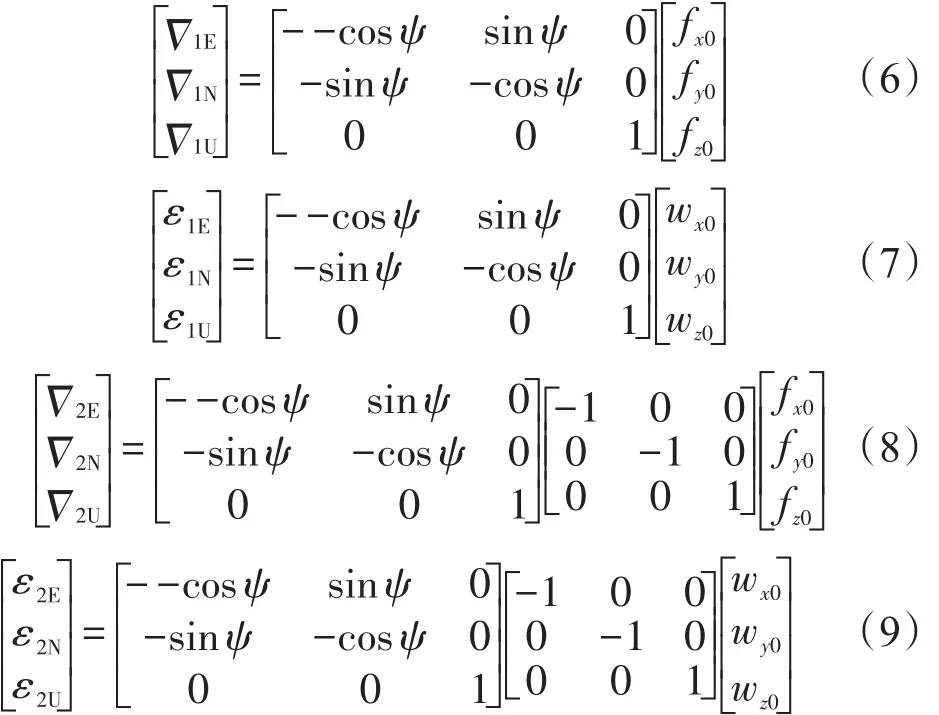
对比式（6）、式（8）与式（7）、式（9），有：

式（10）表明水平近似为0的情况下，180°对位的等效东向陀螺零偏相反，由式（1）知其误差失准角也相反。

假设寻北装置的第二个位置的真实姿态角为［θγψ］，由于三个姿态误差角均为小角度误差，有：

同理，设第一个位置的姿态［θ1γ1ψ1］，由于处在两位置时间相距较短，可近似认为器件的零位基本保持不变，即：ϕ1x≈-ϕ2x、ϕ1y≈-ϕ2y、ϕ1z≈-ϕ2z。第二个位置与第一个位置相差180°。则第一个位置的航向角为：

航向角ψ1、ψ2的取值范围为0°～360°，综合式（1）、式（11）和式（12）得到两位置对消后的航向值ψ以及等效东向陀螺的漂移εE，如表1所示。

表1　双位置对消寻北及测漂公式Table 1　Two position counteract seeking north and gyro bias measure algorithm

1.3双位置陀螺测漂原理

进行双位置寻北计算中，式（6）～式（10）表明水平姿态基本为0的情况下，等效东向陀螺的零偏正好相反。通过对两个位置的航向值进行处理，得到因东向陀螺零位而引起的误差失准角，利用式（11）初略的计算寻北仪的等效东向陀螺漂移，如表1中所示。将等效东向陀螺投影到载体坐标系下，得到载体系中陀螺零位补偿量如式（13）所示。

其中，εbx、εby、εbz为等效东向陀螺在寻北仪x，y，z陀螺的零位补偿量。

2　基于惯性系双位置寻北算法的误差分析

基于惯性系的双位置寻北算法虽然综合了两种算法的优点，但仍有影响寻北精度的误差源存在。因此有必要定量的分析各误差源在算法中对寻北精度的影响。影响算法精度的主要误差源如表2所示。

表2　算法的误差源及表现形式Table 2　Error sources and manifestations of algorithm

为综合分析各误差源对双位置的寻北精度的影响，不妨设第一个位置寻北仪的等效东向陀螺零偏为ε1E，第二个位置寻北仪的等效东向陀螺的零偏为ε2E。根据式（1），得其对准后的方位失准角为：

其中，ϕ1z为第一个位置的寻北航向误差失准角，ϕ2z为第二个位置的寻北航向误差失准角，ε1E0为第一个位置的陀螺固有零位投影成的等效东向陀螺零偏，ε2E0为第二个位置的陀螺固有零位投影成的等效东向陀螺零偏，ε1EM为第一个位置的陀螺地磁零位投影成的等效东向陀螺零偏，ε2EM为第二个位置的陀螺地磁零位投影成的等效东向陀螺零偏。

设第二个位置的真实方位为ψ，则第二位置的方位角为：

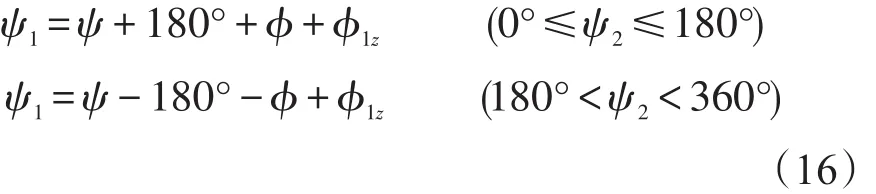
由式 （12）可知在有转位误差情况下，第一个位置的寻北值为：根据双位置对消原理，补偿后的航向角如式（17）所示。其中，φ为转位带来的误差。

因此航向误差失准角为：

根据式（18）双位置寻北误差公式可简化为式（19）。

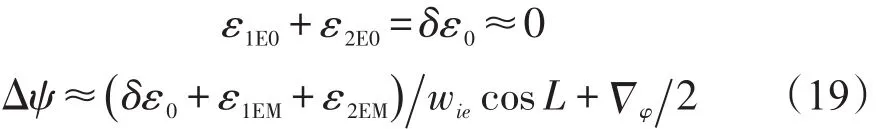
其中， δε0为两段时间内陀螺零位的变化量。

3　实验

新算法效果需要通过三个实验来验证。首先要验证算法中对方位零位的补偿效果，其次是验证算法补偿前后航向精度的变化，最后，在实际使用情况下对算法进行测试。

3.1方位零位补偿实验

将系统置于有方位基准的转台上，转台每隔45°测1个点，一共测8个点，重复2次，第一次用来做补偿系数的计算，第二次做补偿效果的检验。补偿效果如图1所示。

图1　光纤陀螺地磁零位的补偿Fig.1　FOG magnetic bias compensation

由图1可知，补偿前陀螺零位随方位变化最大达到0.15（°）/h，远大于陀螺逐次启动精度。补偿后，陀螺零位的变化在0.1（°）/h以内，已经达到了全方位的精度指标要求，表明补偿降低了由地磁带来的方位零位的变化。

3.2地磁零位补偿对系统精度影响

将系统置于有方位基准的转台上，通过转动转台进行双位置寻北，其姿态误差如图2所示。

由图2可知，方位误差均值在补偿前为30.01mil，而补偿后方位误差均值为3.51 mil。说

Δ明通过地磁零位的补偿，保证了陀螺在两位置寻北过程中零位稳定性，提高了双位置寻北的精度。

3.3晃动基座寻北实验

将系统安装在侦察车的桅杆上，并且桅杆伸到空中进行实际工作状态的测试，结果如图3所示。

图2　地磁零位对寻北精度的影响Fig.2　Effect of magnetic bias to north seeking accuracy

图3　晃动基座下传统与惯性系双位置寻北算法精度比较Fig.3　Comparison between convention and inertial two position seeking north algorithm accuracy under swaying base

由图3可知，晃动基座情况下采用传统算法得到的方位误差一倍标准差为9.36mil，而采用惯性系算法得到方位误差一倍标准差为4.02mil。传统算法之所以离散度大，是由于个别实验误差极大超差造成的，这是因为传统算法中没有隔离外部角运动的影响，而是将其作为等效陀螺零偏考虑到寻北算法中，因而受外界影响较大，精度较低；基于惯性系的双位置寻北算法从原理上隔离了外界晃动对其寻北精度的影响，寻北精度高，受外部晃动条件影响小，其主要寻北误差由两段位置中陀螺零位变化量决定。实测数据结果表明基于惯性系的双位置寻北算法能有效保证晃动情况下的寻北精度，环境适应性优于传统算法。

4　结论

本文对由低精度FOG组成的寻北仪的寻北算法进行了研究。新算法提出了光纤陀螺的零位补偿方法及改进后的双位置寻北算法。通过对陀螺地磁零位的补偿，提高了陀螺的精度，间接提高了寻北的精度。惯性系寻北算法的引入克服了传统双位置寻北算法易受外界干扰的缺点。在车体发动及升降杆升起处在阵风中等一些复杂的外界情况下，车上寻北误差一倍标准差小于4.5mil、极差小于10mil、对准时间小于5min表明新的算法提高了寻北精度，具有较强的环境适应性。

［1］ LONG Wen-qiang，QIN Ji-rong.Design and realization of two-position digitized strapdown north seeker［J］.Fire Control and Command Control，2007，32（4）∶97-99.

［2］Lee J G，Park C G，Park H W.Multiposition alignment of strapdown inertial navigation system［J］.IEEE Transactions on Aerospace and Electronic Systems，1993，29（4）∶1323-1328.

［3］ June Shen，Lingjuan Miao，Weixi Gao，et al，Design and realization of a low-cost，fast and high-precision FOG north finder［J］.International Conference on Electrical and Control Engineering，2010∶695-698.

［4］Hotate Kazuo，Tabe Kunio.Drift of an optical fiber gyroscope cause by the faraday effect∶experiment［J］.Journal of Lightwave Technology，1987，5（7）∶997-1001.

［5］ Shen，Jun，Gao Wei-xi.Research of geomagnetic effect on FOG north-finder［C］.Information Science and Engineering（ICISE），2010 2ndInternational Conference on，2010∶5270-5273.

［6］谷宏强.光纤陀螺捷联惯导系统初始对准技术研究［D］.南京理工大学，2009.GU Hong-qiang.Fiber optic gyro SINS initial alignment technology［D］.Nanjing University of Science and Technology，2009.

［7］王丽芬，谢英，杨功流，等.基于光纤陀螺的捷联寻北仪误差分析［J］.光电工程，2011（5）∶46-51. WANG Li-fen，XIE Ying，YANG Gong-liu，et al.Error analysis of the srtap-down north-finder based on the fiber optical gyroscope［J］.Opto-electronic Engineering，2011 （5）∶46-51.

［8］ T.Gaiffe，Y.Cottreau，N.Faussot，et al，Highly compact fiber optic gyrocompass for applications at depths up to 3000 meters［J］.Underwater Technology，2000∶155-160.

［9］ H.Arditty，H.Lefevre.Theoretical basis of Sagnac effect in fiber optic gyroscopes［M］.Springer Berlin Heidelberg，1982.

［10］秦永元，张洪钺，汪叔华.惯性导航［M］.西安∶西北工业大学出版社，2010. QIN Yong-yuan，ZHANG Hong-yue，WANG Shu-hua. Inertial navigation system［M］.Xi’an∶Northwestern Polytechnical University Press，2010.

Fiber North Finder Two Positions North SeekingAlgorithm Based on Inertial System

JIANG Jie1，HUANG Ming2，YANG Gong-liu1，SHI Jun1，ZHOU Xiao1
（1.School of Instrumentation Science and Opto-electronics Engineering，Beihang University，Beijing 100191；2.Jiujiang Precision Measuring Technology Research Institute，Jiujiang 332000）

The north finder which is composed by low accuracy fiber optical gyroscope（FOG）has a simple structure，low cost advantages except the FOG is vulnerable to external environmental conditions of geomagnetic and complex swaying of the car.In this paper，gyro geomagnetic bias compensation is used to ensure the FOG bias stability，moreover，new two position north seeking algorithm based on inertial system is presented.Algorithm respectively conduct inertial north seeking algorithm in two positions.By using the thought of cancel each other out in two positions，orientation without fixed bias effect will be obtained so as the bias estimation of the horizontal FOG.Experiments show that with gyroscope zero bias stability of 0.15（°）/h and accelerometer bias stability of 150mg，north finder error standard deviation is less than 4.5mil，the range is less than 10mil，alignment time is less than 5min in the car.The good result in practices prove that compared with the traditional two position north seeking algorithm，new method with strong environmental adaptability can keep high alignment precision under swaying base conditions.

low accuracy FOG；geomagnetic bias compensation；inertial two position north seeking algorithm；swaying base

U666.1

A

1674-5558（2016）02-01097

10.3969/j.issn.1674-5558.2016.02.009

2015-03-31

蒋杰，男，硕士，研究方向为惯性导航系统。