非均质变截面杆轴向振动的插值矩阵法分析
葛仁余, 张金轮, 韩有民, 牛忠荣, 程长征, 杨智勇
(1.安徽工程大学 力学重点实验室,安徽 芜湖 241000; 2.合肥工业大学 土木与水利工程学院,安徽 合肥 230009)
非均质变截面杆轴向振动的插值矩阵法分析
葛仁余1,张金轮1,韩有民1,牛忠荣2,程长征2,杨智勇2
(1.安徽工程大学 力学重点实验室,安徽 芜湖241000; 2.合肥工业大学 土木与水利工程学院,安徽 合肥230009)
文章分析了非均质变截面弹性杆轴向自由振动问题,该类杆件的弹性模量、横截面面积和单位杆长质量是截面位置的函数,对于函数的具体形式无任何限制条件。运用插值矩阵法可一次性地计算出各阶振动固有频率,它们具有同阶精度,并可同时获取相应的振型函数。数值计算结果与现有结果对比表明了文中方法的有效性和良好的计算精度。
变截面杆;轴向振动;固有频率;插值矩阵法
变截面杆是工程结构中应用广泛的承力构件,对于变截面杆振动问题,已有研究成果尚缺乏一种计算简单且精度较高的方法。分析结构振动的固有频率问题,李兹法是常用的近似计算方法,但计算精度取决于事先假设的振型函数,对于高阶频率的计算往往不能达到满意的效果。文献[1-3]用不同的方法对均质变截面杆进行了大量的研究,这些解法不同程度地存在计算方法复杂、求解精度不好的缺点;文献[4]建立了均质变截面直杆纵振动的频率方程,将小波分析理论与微分求积法相结合求解微分方程,对其振动频率进行了分析;文献[5]根据均质变截面直杆的纵振与等截面直梁的弯曲问题的一些相似性质,把求变截面直杆纵振函数变为求梁弯曲时的截面上的弯矩问题,对应于杆的横截面面积的某些变化规律,得到了求杆的纵振函数及固有频率的计算公式。
随着航空航天工业的飞速发展,非均质变截面直杆振动问题也引起了人们的普遍重视。在工程结构的优化设计中,为了达到强度和质量的最佳分布或满足结构功能的要求,常常使用非均质变截面直杆类构件。但非均质变截面弹性直杆的轴向自由振动的控制方程是变系数二阶偏微分方程,现有的解析方法只能得到一些特殊类型的非均质变截面直杆的振动方程的精确解,例如楔形体和锥体、截去尖端的楔形体和锥体、弯曲刚度随长度坐标以任意幂函数变化的悬臂直杆等。文献[6]获得了计算微弱楔形直杆固有频率的简便公式,但该公式对截面变化很大的楔形直杆不能使用;文献[7]获得了弹性模量、密度和截面面积以指数形式变化时的直杆纵振和扭振的一个通解,但求解固有频率时计算量特别大且解的形式比较复杂;文献[8]采用摄动法得到了该类直杆纵振的固有频率和振型,但也只适用于弹性模量、密度和截面面积变化微弱的直杆;文献[9]借助积分方程理论得出一种计算非均质变截面直杆的振动频率和振型的方法。
本文从非均质变截面杆件一般形式的振动微分方程出发,将非均质变截面杆件振动频率的计算转化为常微分方程组的特征值求解,运用插值矩阵法求解常微分方程组特征值问题,可获得杆件轴向振动所有频率,同时相应的振型一并解出。插值矩阵法原理简单、易于计算、实用性好、计算精度高,能灵活适用于任意变截面弹性直杆的轴向自由振动问题。
1 非均质变截面杆轴向振动微分方程
1.1振动微分方程的建立
一变截面杆件如图1所示。
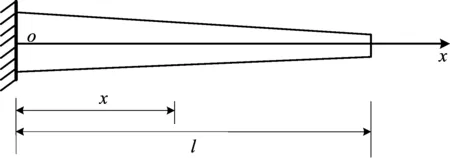
图1 变截面杆
设杆件固有轴向振动位移为w(x,t),则非均质变截面杆轴向振动的平衡微分方程[3]为:
(1)
将(1)式展开,则有:
(2)
当非均质变截面杆做固有振动时,设其解为:
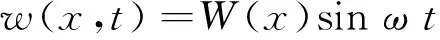
(3)
其中,W(x)为杆件轴向振动的振型函数;ω为杆件轴向振动的固有频率。将(3)式代入(2)式可得非均质变截面杆轴向振动的微分方程为:
(4)
其中,E(x)、A(x)、ρ(x)分别为变截面杆弹性模量、截面面积和密度,皆为截面位置x的函数。
设ξ=x/l,则有0≤x≤l,ξ∈[0,1],单位化后(4)式转化为:
(5)
由于(5)式中含有ω2项,引入新变量g(ξ),消去(5)式中含ω2的非线性项,组成新的方程组如下:
(6)
当材料为均质材料时,E(ξ)=E,ρ(ξ)=ρ,由(6)式可得均质材料变截面杆轴向振动的方程为:
(7)
从而,非均质和均质变截面杆轴向振动固有频率分析转化为求解常微分方程组(6)式、(7)式的常微分方程组特征值问题。
1.2轴向振动微分方程的边界条件
将(3)式代入下列3种情形,于是将杆端边界条件转化为以下表达形式。
情形1一端固定、一端自由的杆件轴向振动边界条件为:
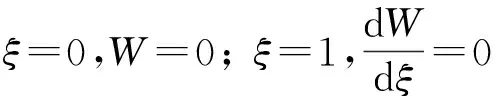
(8)
情形2两端自由的变截面杆件,其轴向振动边界条件为:
(9)
情形3大头固定、小头有弹性支承(设其弹性刚度为k)变截面杆件,其轴向振动边界条件为:
(10)
至此,非均质变截面杆件轴向振动频率ω的计算归结为求解在边界条件(8)~(10) 式下线性常微分方程组(6) 式的特征值问题。一般需要数值方法求解这类问题,本文采用插值矩阵法计算[10-12]。
2 常微分方程组特征值问题求解
针对一般的常微分方程组两点边值问题,A.Φ.斯米尔诺夫用拉格朗日多项式插值创立了积分矩阵法,求解区间最多分为7段。文献[11]在积分矩阵法基础上建立了插值矩阵法,采用了分段多项式插值,使得求解区间可以任意等分,计算值可达到充分高的精度。假设一个含r个方程的线性常微分方程组特征值问题为(11)式,相应的边值条件为(12)式,即
(11)
(12)
插值矩阵法将求解区间[xa,xb]剖分为n+1个节点、n个子区间,在每个子区间上使用低阶分段多项式函数插值逼近待求函数,以常微分方程组中出现的最高阶导数在离散节点上的值作为离散系统的未知参数,形成代数特征值方程组,解之可以获得特征值与相应的特征函数。该方法可以同时求解出常微分方程组特征值问题中出现的所有函数和其各阶导数,且具有同阶精度。本文采用插值矩阵法来求解非均质变截面杆件轴向振动频率的常微分方程组特征值问题。
3 算例分析
算例1设一直杆的弹性模量、横截面面积、密度均以指数函数变化,即
(13)
其中,α、β、γ为常数;E0、A0、μ0分别为ξ=0处的弹性模量、横截面面积和单位杆长的质量。将(13)式代入(6)式得:
(14)
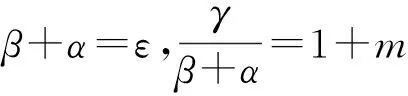
(15)
令
(16)
将(16)式代入(15)式可得:
(17)
引入新函数g(ξ)=λW(ξ),则(17)式变换为:
(18)
由插值矩阵法求解常微分方程组(18)式,可以获得非均质变截面杆在一端固定另一端自由和两端固定的边界条件下微分方程的特征值λ,再由(16)式可以获得轴向振动的固有频率如下:
(19)
本文解与文献[2]解、文献[13]解、Bessel解、精确解的对比见表1、表2所列。由表1、表2可见,当m=0,ε=1/2时,本文计算结果与精确解吻合良好,插值矩阵法计算精度比文献[2]解和文献[13]解要高。同时本文方法还给出了m、ε为其他任意值时的计算结果,而m、ε为其他任意值时获得精确解是十分困难的,所以这也是本文方法的一个显著优点。
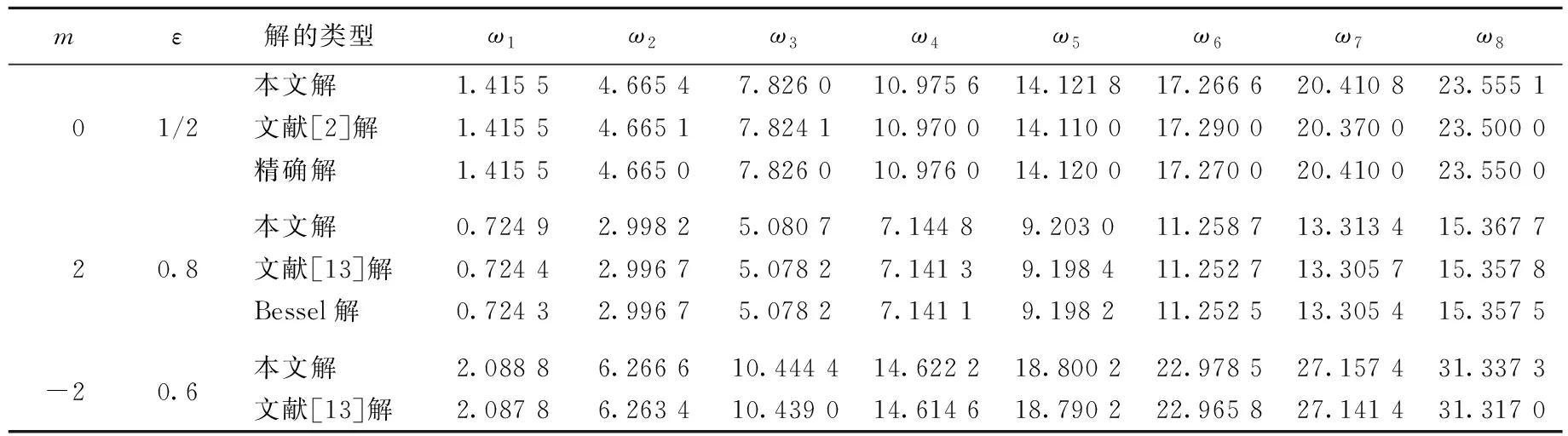
表1 算例1一端固定、另一端自由变截面杆轴向振动前8阶固有频率 Hz
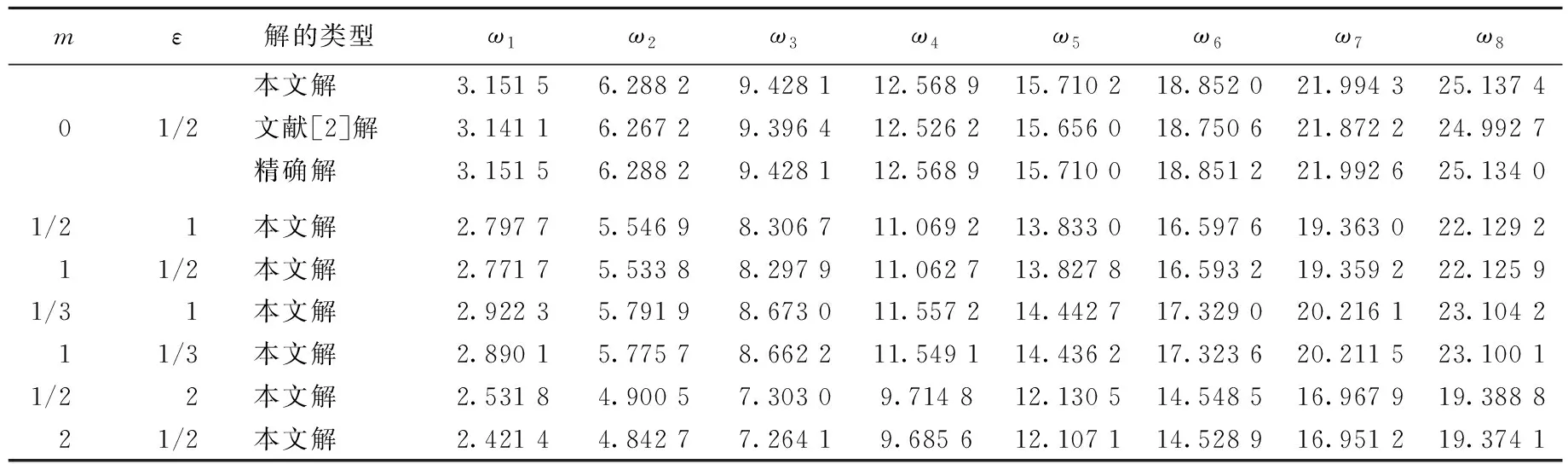
表2 算例1两端固定变截面杆轴向振动前8阶固有频率 Hz
算例2设非均质变截面弹性直杆的参数为:
(20)
其中,E0、A0、μ0分别为ξ=0处的弹性模量、横截面积和单位杆长质量。将(20)式代入(6)式得:
(21)
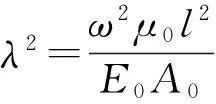
(22)
引入新函数g(ξ)=λW(ξ),则(22)式变换为:
(23)
因此,非均质变截面弹性直杆轴向振动固有频率及其相应振型的计算,转化为由插值矩阵法求解常微分方程组(23)式特征值问题。由本文方法计算出一端固定、另一端自由的非均质变截面杆轴向振动前8阶固有频率,并与文献[2]和文献[14]计算结果比较,见表3所列。由表3可见,本文方法计算值与已有结果吻合良好,再次证明了本文方法的有效性。由本文方法计算两端固定非均质变截面杆轴向振动前8阶固有频率,结果见表4所列。

表3 算例2一端固定、另一端自由变截面杆轴向振动前8阶固有频率 Hz

表4 算例2两端固定变截面杆轴向振动前8阶固有频率 Hz
本文方法可计算出(3)式中非均质变截面杆轴向振动的前若干阶固有频率ωn,同时相应的振型W(ξ)也一并解出。表3中前4阶固有频率所对应的振型函数W(ξ)的分布曲线如图2所示。
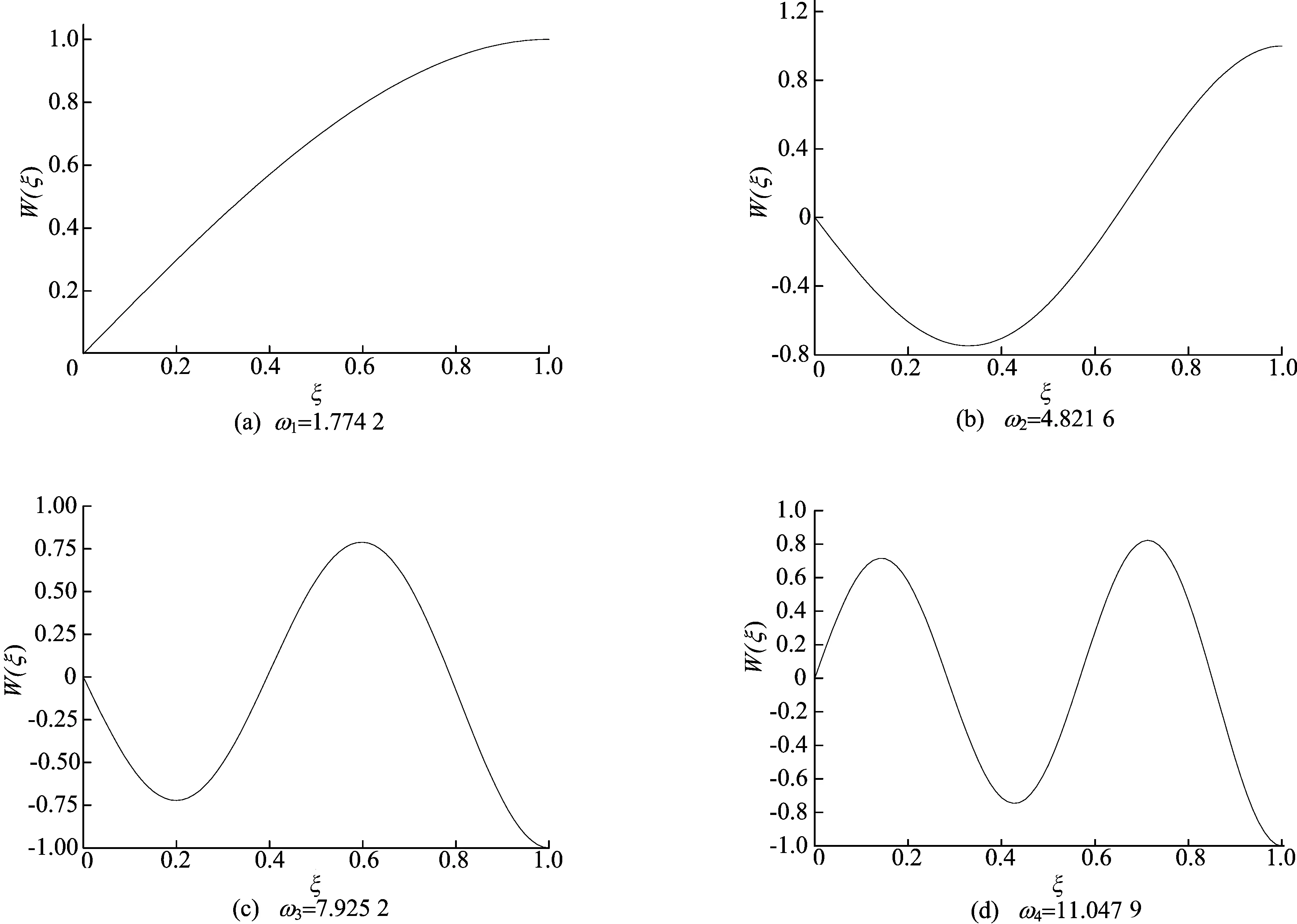
图2 变截面杆轴向振动前4阶固有频率对应的振型
4 结 论
本文从非均质变截面杆件一般形式的振动方程出发,采用变量代换法,将关于非均质变截面直杆轴向振动固有频率的一组非线性常微分方程的特征值问题转化为线性特征问题,用插值矩阵法求解,获得了轴向振动固有频率及相应的振型。本文方法可一次性地计算出非均质变截面直杆轴向振动所有固有频率和相应的振型函数,克服了其他方法的一些缺点,如计算方法复杂、求解精度不好等;求出的同一阶振型函数及其各阶导数的计算精度是同阶的,在利用振型的一阶导数计算振动结构应力场时,这是一个显著优点;本文方法数值计算结果与现有结果吻合良好,表明了本文方法的有效性和良好的计算精度;本文方法适用于任意变截面弹性直杆的轴向自由振动问题,在计算复杂工程结构振动的固有频率和振型方面具有较高的计算精度和一定的工程应用价值。
[1]侯祥林,范炜,贾连光.变截面压杆临界荷载的迭代算法[J].哈尔滨工业大学学报,2011,43(增刊1): 237-240.
[2]黎明安,王忠民.非均质变截面弹性直杆纵向自由振动的差分解法[J].力学与实践,1992,14(2): 32-35.
[3]张瑞平.可展为幂级数的变截面弹性直杆的纵向自由振动分析[J].机械科学与技术,2000,25 (增刊1): 61-62.
[4]张菊梅,赵凤群,党晓敏.变截面弹性直杆纵振动分析的小波-DQ法[J].力学与实践,2010,32(4): 71-73.
[5]袁镒吾,李志坚.变截面直杆纵向自由振动的一种解[J].工程力学,1996,13(3):105-113.
[6]刘先志.推算楔形直杆纵振与扭振自主频率的一个方法[J].中国科学,1977,6(2): 536-546.
[7]刘先志.关于非均质变截面弹性直杆的纵向自主振动[J].应用数学和力学,1980,1(2):237-245.
[8]周叮.非均质变截面弹性直杆纵向自由振动的渐近解法[J].力学与实践,1990,12(4):16-19.
[9]许明田,周学圣,程德林.一种研究非均质变截面弹性直杆振动的新方法[J].山东工业大学学报,1992,22(2):7-12.
[10]葛仁余,程长征,牛忠荣,等.各向同性材料切口尖端热流密度奇性特征分析[J].合肥工业大学学报(自然科学版),2014,37(3):281-285.
[11]牛忠荣.两点边值问题的插值矩阵法及误差分析[J].合肥工业大学学报(自然科学版),1993,16(1):25-32.
[12]杨智勇,牛忠荣,葛仁余,等.功能梯度叠层厚板弯曲半解析求解[J].合肥工业大学学报(自然科学版),2016,39(3):355-359.
[13]吴晓,姚春梅,张龙庭.再谈“非均质变截面弹性直杆的纵向自主振动”[J].陕西工学院学报,1995,11(1): 26-29.
[14]庞家驹.机械振动习题集[M].北京:清华大学出版社,1982:235-236.
(责任编辑张淑艳)
Longitudinal vibration analysis of nonuniform elastic straight bar with variable cross-section by interpolating matrix method
GE Renyu1,ZHANG Jinlun1,HAN Youmin1,NIU Zhongrong2,CHENG Changzheng2,YANG Zhiyong2
(1.Key Laboratory for Mechanics, Anhui Polytechnic University, Wuhu 241000, China; 2.School of Civil and Hydraulic Engineering, Hefei University of Technology, Hefei 230009, China)
This paper deals with the longitudinal vibration problems of functions of section location of elastic straight bar including elasticity modulus, section area and mass per unit length under the normal conditions. There is no restriction to the specific form of function. By applying the interpolating matrix method to solving the established equations, all the natural frequencies of longitudinal vibration companying with the corresponding vibration mode functions of bar with variable cross-section are calculated at a time. All the calculated natural frequencies of longitudinal vibration have the same high accuracy. The numerical results show that the computed results from the presented method have very high accuracy compared with the existing solutions.
variable cross-section bar; longitudinal vibration; natural frequency; interpolating matrix method
2015-03-30;
2016-06-18
国家自然科学基金资助项目(11272111;11372094);安徽省高校自然科学研究重点资助项目(KJ2016A055)
葛仁余(1969-),男,安徽合肥人,博士,安徽工程大学副教授;
牛忠荣(1957-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师;
10.3969/j.issn.1003-5060.2016.08.016
O326
A
1003-5060(2016)08-1084-05
程长征(1979-),男,安徽太湖人,博士,合肥工业大学教授,博士生导师.

