基于身高和拃长数据的性别分类研究

王泽昕陕西省商洛中学

基于身高和拃长数据的性别分类研究

王泽昕
陕西省商洛中学

本文以身高和拃长②数据为特征，对男女性别进行分类，采用的分类方法为最小错误率贝叶斯决策。本文统计了样本数为25时的决策分类详细结果，并研究了样本数为5～50时错误率的变化趋势。研究结果表明，以身高和拃长数据为特征时，能够较为有效地区分出男女性别，且当训练集样本数量逐渐增大时，错误率显现出逐渐减小的趋势。

性别分类；模式识别；贝叶斯决策；Matlab编程

1.引言

模式识别（也称模式分类）是指对表征事物或现象的各种形式的（数值的、文字的和逻辑关系的）信息进行处理和分析，以对事物或现象进行描述、辨认、分类和解释的过程，是信息科学和人工智能的重要组成部分，被广泛运用与文字识别、语音识别、指纹识别、遥感、医学诊断等领域。

性别分类是模式识别领域中广受关注的一个问题，它能体现男女性别在某些方面的差异，为人体生理学和心理学等方面研究提供理论基础和数据支持。目前，已有学者进行了人脸特征性别分类［1］［2］、社交媒体使用习惯的性别分类［3］、触觉经验性别分类［4］、基于语音的性别分类［5］、基于头发信息的性别分类［6］、基于步态的性别分类［7］等。

本论文将研究利用人体某些数值型的生理数据（身高与手掌长度）进行分类，以探索出性别分类的简易、方便的模型和方法，同时加深人们对男女性别与生理特征之间的关系的理解。模式识别包含许多种分类方法，能够对许多领域的问题进行数据处理和分析。本课题采用最小错误率贝叶斯决策方法，以人体的身高和拃长数据为特征，对数据集进行性别分类。本课题的特征数据易于搜集和处理，且分类错误率较低，有力地体现了男女性别在这两种体征上的差异性。

2.分类方法介绍

分类可以看成一种决策过程，也即我们根据对样本的观测做出其应归属哪一类的决策［8］。我们采用的分类方法为最小错误率贝叶斯决策。下面我们将详细介绍最小错误率贝叶斯决策的决策原理。

在这里，我们仅讨论两类的情况：记类别为ω1和ω2，假设现在我们已知数据的特征x，用P（ω1|x）和P（ω2|x）分别表示此时两类的后验概率。所谓后验概率，是指某事件已经发生，要求该事件发生的原因是由某个因素引起的可能性的大小。例如，此处的P（ω1|x）和P（ω2|x）分别表示，在已知我们观测到数据特征为x时，造成我们观测到特征为x的原因分别是由于该数据属于ω1和ω2的概率。

根据贝叶斯公式，我们可以将P（ωi|x）（i=1，2）表示为：

其中P（ωi）（i=1，2）为ω1和ω2这两类的先验概率。所谓先验概率，就是在事件还没有发生，要求这件事情发生的可能性的大小。在此处，先验概率P（ωi）（i=1，2）是指我们还没有开始进行观测样本时，ω1类和ω2类的概率。通常可以用预先知道的知识（例如ω1类和ω2类的数量占比）来得到。

在一般的模式识别问题中，我们往往希望尽量减少分类的错误率，即目标是追求最小错误率。从这一目标要求出发，利用（2-1）中的贝叶斯公式就能得出使得错误率最小的分类决策，称之为最小错误率贝叶斯决策。最小错误率贝叶斯决策可描述为：

P（x|ωi）（i=1，2）的具体值可由训练集数据在一定分布假设下求得。通常我们可认为人群中的身高和拃长分布满足正态分布，双变量正态分布联合概率密度函数公式为如下：

其中-∞＜x，y＜+∞；-∞＜μ1，μ2＜+∞；σ1，σ2＞0；-1≤ρ≤1。其中μ1，μ2分别为x和y的均值，σ12，σ22分别为x和y的方差，ρ为x 和y的相关系数。

3.研究方案设计

3.1数据集说明

本课题所采用的数据集来自于宾夕法尼亚州立大学Mind on Statistic公开数据库①。该数据集包含167名大学生的身高（单位：英寸）与拃长数据（单位：厘米），其中女性89名，男性78名。

我们在数据集中随机挑选一定数目的数据作为训练集（训练集中男女性别数量一致），而测试集为整个原始数据集。我们首先选取了样本数为25的训练集，对最小错误率贝叶斯分类器进行训练，得到参数。为了研究训练集大小对分类效果的影响，我们研究并记录了训练集大小为5～50的情况下分类错误率，并绘制了错误率随训练集大小变化的趋势图，具体结果见第4章。

3.2整体错误率的计算

整体错误率的计算公式如下：

也即整体错误率是各类错误率的加权平均和，各类的错误率的权重即为该类的先验概率。其中P（ω1）和P（ω2）分别代表ω1类和ω2类的先验概率，e1和e2分别代表ω1类和ω2类的分类错误率。e1与e2的计算公式如下：

3.3仿真环境介绍

在本课题中，我们采用MATLAB作为仿真环境。MATLAB是美国Math Works公司出品的商业数学软件，在数值计算方面具有强大的能力，被广大科研人员和工程技术人员所采用。我们主要用MATLAB的m文件编程功能来进行数据的预处理、最小错误率贝叶斯分类器的建立以及决策分类过程的实现。

3.4 MATLAB程序设计框架

本课题的MATLAB程序设计思路及流程如下：

（1）数据预处理。首先将公开数据集导入到Excel表格中，然后利用MATLAB的m文件编写读取数据的函数，将数据读取到MATLAB工作空间中。

（2）设定训练样本数量，从数据集中随机选取一定数目的样本作为训练集。根据训练样本计算公式（2-3）中的μ1，μ2，σ12，σ22，ρ，以便后续建立最小错误率贝叶斯分类器。

（3）根据（2）中计算结果，结合（2-3）可得P（x|ωi）（i=1，2）的表达式，并结合（2-2）建立最小错误率贝叶斯分类器。

（4）利用（3）中建立的最小错误率贝叶斯分类器，对测试集每个样本进行决策分类，决策分类的依据为（2-2）。

（5）利用公式（3-2）和公式（3-3）计算ω1类和ω2类的错误率，并利用公式（3-1）计算整体错误率，以判断决策效果。先验概率P （ω1）和P（ω2）均取0.5，即默认男女比例为1:1。这和我们的日常生活经验是一致的。

（6）改变样本大小，将样本大小从5取到50，分别统计不同样本大小下的的整体错误率。

4.决策分类结果

我们采用Matlab建立最小错误率贝叶斯分类器，首先在样本大小为25的情况下进行决策分类。决策分类中间过程参数值及最终错误率见表4.1。

表4.1　样本数为25时的决策分类结果记录表

接下来，我们对训练集大小为5～50的情况进行了分类，共计46次分类实验。为了减小数据随机噪声的影响，在每次分类实验中，我们进行了共计10次测试，并统计每次测试的错误率，而后求取平均值，作为最终的错误率。46次实验对应的错误率与训练集大小之间的关系记录如表4.2，变化趋势图如图4.1：

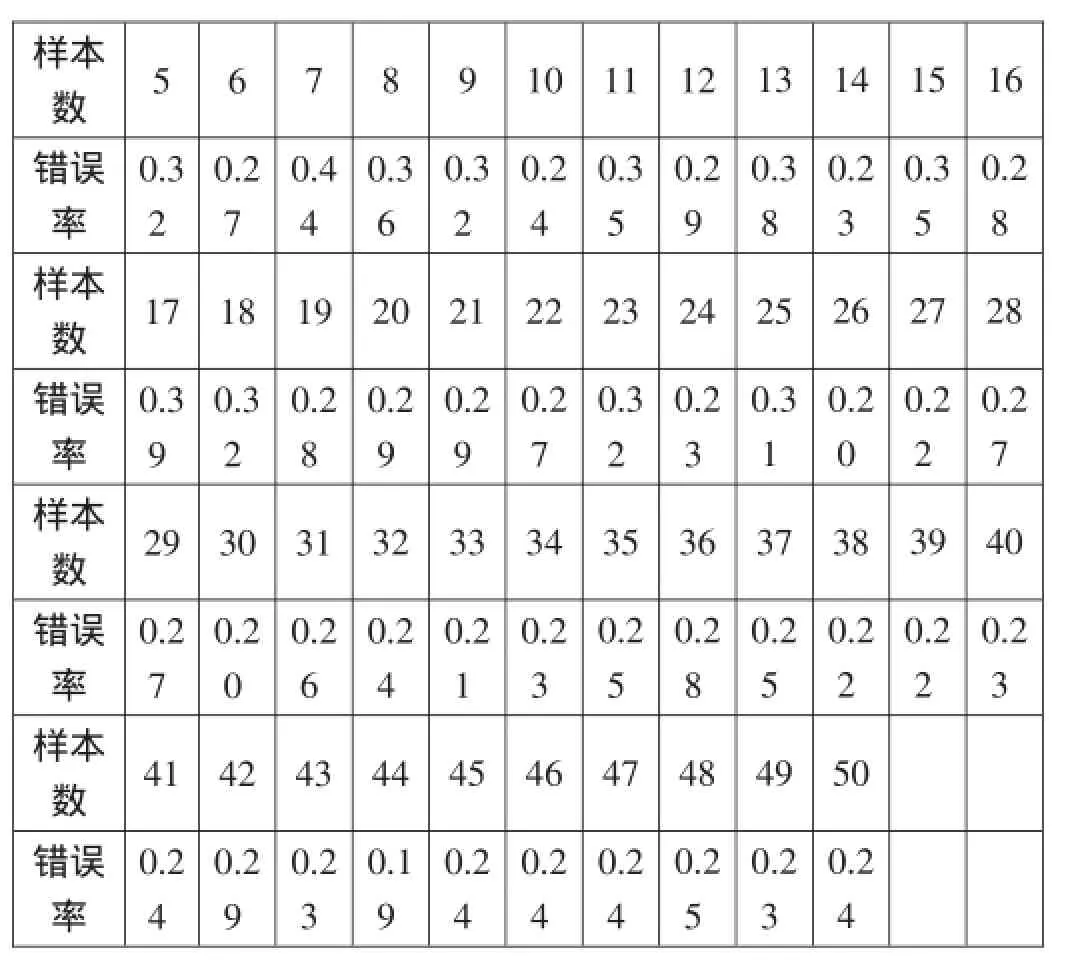
表4.2　样本数为5～50时的决策分类结果记录表

由表4.2和图4.1可见，分类错误率随着训练集的增大有减小的趋势。

5.总结

性别分类是模式识别领域中广受关注的一个问题，它能体现男女性别在某些方面的差异，为人体生理学和心理学等方面研究提供理论基础和数据支持。本文采用最小错误率贝叶斯决策方法，利用宾夕法尼亚州立大学Mind on Statistic公开数据库的数据集，对身高和拃长数据集进行性别分类。本课题的算法实现相对简单，且数据易于搜集和处理，分类结果较为明显。同时，我们发现，分类错误率随着训练集的增大有减小的趋势，说明在有条件的情况下应选取尽可能多的数据作为训练集。

注释：

①Data Sets for Mind on Statistics（Utts and Heckard）:http:// sites.stat.psu.edu/～rho/mindon/readme.htm l

②拃长：指一个人张开大姆指和中指（或小指）两端的距离。

［1］赵海英，杨一帆，徐正光.基于多角度LBP特征的三维人脸性别分类［J］.自动化学报，2012，09:1544-1549.

［2］武勃，艾海舟，肖习攀，徐光祐.人脸的性别分类［J］.计算机研究与发展，2003，11:1546-1553.

［3］王晶晶，李寿山，黄磊.中文微博用户性别分类方法研究［J］.中文信息学报，2014，06:150-155+168.

［4］崔倩，叶浩生.触觉经验对性别分类的影响:具身的视角［J］.广州大学学报（社会科学版），2013，03:41-45.

［5］高原.基于性别分类的说话人识别研究［D］.江苏师范大学，2012.

［6］刘爽，谢金融，吕宝粮.基于头发信息的性别分类［J］.计算机仿真，2009，02:212-216.

［7］余美霞.基于步态的性别分类研究［D］.北方工业大学，2013.

［8］张学工.模式识别［M］.第三版.北京:清华大学出版社，2010:13-13.

王泽昕（1999-），男，汉族，陕西省商洛人，就读于陕西省商洛中学，高中在读，研究方向机械自动化与智能系统。