整体法与隔离法的应用探究

张少伍+杜书林

摘 要： 分析一个动力学系统的运动状态时，需要注意研究的问题属于系统内部之间的作用力，还是系统与外部之间的作用，进而采取的研究方法也就不同，即整体法与隔离法，中学物理中大多数动力学情况属于整体法与隔离法相结合同时进行研究，才能使问题简化易懂。

关键词： 系统 整体法 隔离法

1. 方法解读

在处理中学物理题的时候，选择正确的解题方法往往是解决问题的关键。通过对近年高考物理试卷的分析不难发现，整体法与隔离法一直都是高考热点。但掌握这一方法的学生并非很多，往往处理问题时不知所措，所以有必要探究整体法与隔离法的具体应用。

“整体法”，顾名思义，就是利用整体的思维分析问题并解决问题，是系统论中“整体原理”在物理学中的应用。这种方法研究的对象是整个系统，从整个过程或整体揭示事物的本质，探索事物的运动规律。中学物理教学中，我们不能单抓局部事物规律不放，更多则是放眼全局，重在培养学生用整体思维分析物理问题的能力。用整体法解决问题时，可先从分析物理过程的角度出发，也可选择物理状态变化的全过程进行研究，或者选择整个系统作为研究对象，分析整个系统的运动状态，这些统称为“整体法”。与整体法对应的“隔离法”，则是把整个系统过程中的单一过程分离出来或把某个即要研究的物体从整个系统中分离出来进行研究的方法。我们有时会遇见求解一个系统内部物体间的相互作用力，对于这种情况一般采用的研究方法都是“隔离法”，即把要研究的物体从整个系统中分离出来。同样，若求解某一过程中的物理量，一般而言把这个状态从整个过程中隔离出来进行分析，这种方法我们称之为隔离法。

2.例题解析

那么怎样利用整体法与隔离法到具体问题中呢？可以结合两个实例进行分析。

通过分析可知，本题考察的重点是摩擦力的产生条件及力的平衡条件这两个知识点。分析如下，虽然受到水平力F=5N和F=10N的作用力，但是a，b，c三个物体始终处于一种静止平衡状态，那么我们可以把a，b，c三个物体看做一个整体系统，要是研究这个系统和外界之间的作用力就可以采用整体法，则物体c与地面之间的作用力大小F就是系统在外力F=5N，F=10N作用下受到的地面对系统即对物体c的摩擦力F=5N；接下来分析物体a，b之间的作用力F，由于物体a，b之间无相对滑动的运动趋势，则采用隔离法将物体a从整个系统中隔离出来，发现这个物体a，b之间的内力F=0N；接下来继续分析物体b，c之间的作用力，同样采用隔离法，发现由于物体a，b之间无作用力，物体b又受到向左的力F=5N，则由受力平衡条件可知b，c之间必受到向右的摩擦力F=5N。即选项C正确。这种就是非常典型的整体法与隔离法的应用，不过我们很容易发现这个系统是处于静止状态下采用的这种方法，那么运动的系统呢？接下来会发现运动的系统同样可以采用整体法与隔离法。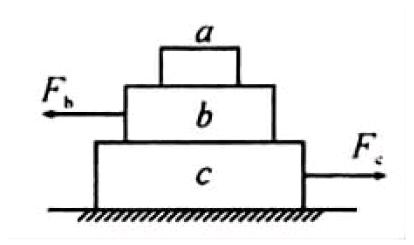

（2）如图，bc为在小车上固定的水平横杆，物块M套在杆上，依靠摩擦力保持相对于横杆静止状态，M又通过轻细线悬吊着一小铁球m，此刻小车正以大小为a的加速度，向右做匀加速，而M，m均相对小车静止，细线与竖直方向的夹角为θ，小车加速度逐渐变大，M始终和小车保持相对静止状态，当加速度增加到2a时候（ ）

A.横杆对M摩擦力变到原来的2倍

B.横杆对M弹力保持不变

C.细线与竖直方向的夹角变成原来的2倍

D.细线的拉力变成原来的2倍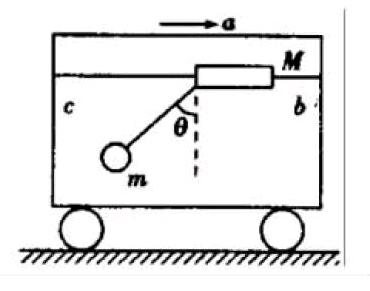

对于这类情况我们会发现这类物体组成的系统处于一种运动的状态中，对于这种情况，我们要分别对系统的水平方向和竖直方向都进行分析。首先分析可知，这个系统是由小铁球m和物块M及细线组成的，我们会发现整个系统处于一种以加速度为a向右匀加速直线运动的状态。通过受力平衡条件可知，竖直方向上系统自身的总重力和横杆对系统的支持力受力平衡，而在水平方向上系统则需满足牛顿第二定律F=（M+m）a所述，其中F表示横杆对M的摩擦力。因小车的加速度逐渐变大，而M和小车始终保持相对静止，那么当系统加速度成为2a后，横杆对M的竖直弹力保持不变，而在水平方向上我们可以知道系统的加速度为2a，M的加速度也为2a，m的加速度也是2a，通过牛顿第二定律，可知横杆对M的摩擦力将变为原来摩擦力的2倍。这是采用整体法分析系统与外力之间作用力；那么分析细线的拉力则属于系统之间的相互作用力，需采用隔离法进行分析，这时我们把小球隔离出来作为研究对象，细线拉力的水平分力为小球提供加速度，当系统的加速度增到2a时候，小球m的加速度也增到2a，这时候细线的竖直分立与小球的重力平衡仍保持不变，然而提供加速的水平分力则需加倍，这个可由牛顿第二定律可得。结合上述分析，可知此答案为A，B。

3.总结研究

对于中学物理中整体法与隔离法的使用不外乎最根本的目的，使我们研究的问题系统化、简单化，总的来说当我们面临的是连接体问题时，通常采用的是隔离法，不过有时也采用整体法处理问题；其次如果一个系统中的研究对象少，首先通常采用的方法是整体法，这样便于我们求解，其次再隔离系统中的某一个物体，采用隔离法进行求解；此外若研究的问题不涉及物体间的相互作用力，或者物体系统内的运动状态相同时，一般优先考虑整体法的使用；最后我们要知道，对于动力学问题，不论是平衡下的系统还是运动中的系统，单纯采用整体法或隔离法不能很好地解决问题，通常采用整体法与隔离法相结合的方法对问题进行研究。

参考文献：

[1]郭亨强.高中物理解题思想方法例谈[J].广东教育：教研版，2007.

[2]胡毓莹.活用整体法与隔离法[J].中学课程辅导.教学研究，2012.

[3]李重安.隔离法与整体法在高中物理解题中的应用[J].高考，2013.