用递推关系推导多层介质膜中的菲涅尔系数

孙　坚，徐遥先，汤丽丽

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.南京邮电大学 海外教育学院，江苏 南京 210023；3.苏州科技大学 电子与信息工程学院，江苏 苏州215009）

用递推关系推导多层介质膜中的菲涅尔系数

孙坚1，徐遥先2，汤丽丽3

（1.苏州科技大学 数理学院，江苏 苏州 215009；2.南京邮电大学 海外教育学院，江苏 南京 210023；3.苏州科技大学 电子与信息工程学院，江苏 苏州215009）

研究多层介质膜中菲涅尔系数的递推关系。从理论上对电磁波在多层介质膜中传播时的菲涅尔系数（反射系数和透射系数）进行分析和推导，并将其写成一个简单紧凑的递推关系以避免类似在教材中出现繁琐冗长的多项式。结果表明，电磁波不管经过多少层中间介质，菲涅尔系数都可以统一成一个简单的递推关系。

菲涅尔系数；递推关系；反射系数；透射系数；多层介质膜

电磁波在多层介质系统传播时的菲涅尔系数（反射系数和透射系数）是电磁理论的研究内容之一。许多课题譬如分层介质中光的传播特性［1-2］；Goos-Hänchen位移［3］和Imbert-Fedorov位移［4］；多层介质膜中的偶极辐射［5-6］、介质表面［7］和平面腔［8-9］中的光散射；多层介质膜［10-11］、复合介质材料［12-13］之间的Casimir效应等都会直接或间接涉及菲涅尔系数的计算。

通常，在计算少数几层介质膜的菲涅尔系数时，可以用教材介绍的方法直接求解。但是，随着层数的增加，这种方法会因为出现繁琐冗长的迭代多项式而变得不实用［14-15］。因此，如何能简便的求解更多层复杂系统的菲涅尔系数成为了人们的研究课题之一。其中，转移矩阵法［1-4，16］是求解菲涅尔系数可行的一种方法，但是这种方法对于理论推导、矩阵运算和计算机编程的要求较高，掌握起来有一定难度。针对这一现状，笔者从菲涅尔系数的定义出发，理论上研究多层介质系统的菲涅尔系数，推导得到一个简单紧凑的递推关系，并且证明它们的等价性。结果表明，电磁波不管经过多少层中间介质，菲涅尔系数都可以统一成一个简单的递推关系。对其进行编程，人们可以很方便地计算得到多层介质膜体系任何层的菲涅尔系数。

1　多层介质膜的菲涅尔系数的理论推导

在真空中，考虑一个由若干层各项同性、线性介质组成的多层介质膜系统（0…N≡0/N，最左侧0层和最右侧N层均是真空介质），选取其中一部分连续介质层（从左侧J层介质和右侧M层介质（可简化为J/M=J…M））作为研究对象，K层表示J和M层之间的某一中间层，如图1所示。这部分连续介质层的菲涅尔系数为反射系数rJ/M和透射系数tJ/M。设电磁波沿z方向传播 （取z方向为正方向）。任一K介质层厚度范围为0≤z≤dK，最外侧层K=0和K=N的坐标则分别为-∞≤z≤0和0≤z＜∞。为了强调中间层的存在，J/M=J…M亦可表示为J/K/M=J…K…M，并且满足rJ/M=rJ/K/M和tJ/M=tJ/K/M。

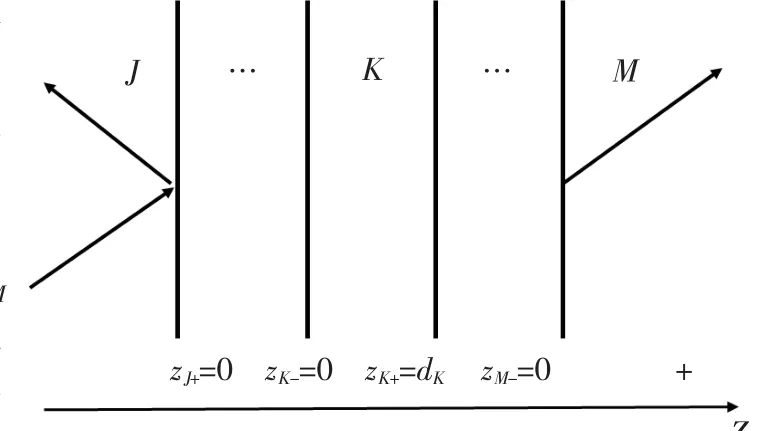
图1　多层介质系统，电磁波从左侧的J层介质入射，经过多层介质的传递，最后从右侧M层介质射出。K表示第J和M层之间的某一中间层

当电磁波斜入射到该系统时，在中间K层介质中的局域电场可以表示为

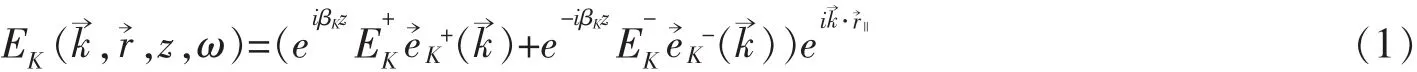
根据菲涅尔系数的定义［6］，两层连续介质组成的介质膜的反射系数r是仅考虑两层之间分界面处的反射波与入射波的电场振幅的比值，透射系数t是仅考虑两层之间分界面处的透射波与入射波的电场振幅比值。

基于定义，可以直接推导多层介质膜中的J层和M层介质之间菲涅尔系数rJ/M和tJ/M的递推关系。首先，推导电磁波从左侧J层入射到J/M系统（如图1所示）时的反射系数rJ/M。根据假设可知，EM-=0，同时定义J/M系统的反射系数

然而，当电磁波入射到J层和M层介质之间某一中间层K层时，其中一部分可以反射回J层介质，还有一部分会继续透射至M层介质。因此，rJ/M也可以通过从K层反射回J层介质的部分计算得到。根据电场在相关介质层之间的边界条件，并根据菲涅尔系数的定义，可以得到电场振幅的关联方程

同样地，多层J/M介质系统的透射系数tJ/M可以表示为

当电磁波传播到中间层K层时，有一部分会透射至M层介质，并且振幅EM+和EJ+与（3）-（5）式相关，于是（3）可以替换成

不难看出，（6）、（9）两式的递推关系很像教材中菲涅尔系数的标准形式，但这相对于JK/M≡JK…M系统而言，确实减少了许多冗长的多项式。通常用这种方法可以求出连续介质膜整体和局部分层的菲涅尔系数。

在描述电磁波在多层介质膜结构中的传播特性的教材中，关于在两种相邻介质（如J层和K层）单界面上的反射系数rJ/K和透射系数tJ/K的计算是研究菲涅尔系数的重要内容。当具有波矢平行分量k的电场入射到某一介质K层时，它的单位向量可以描述成［9，11］

在此基础上，运用电场在J层和K层介质分界面上的边界条件，并根据上述菲涅尔系数的定义，可以推导出标准的单界面反射和透射系数。对s波，其反射系数和透射系数分别为

对p波，其反射系数和透射系数分别为

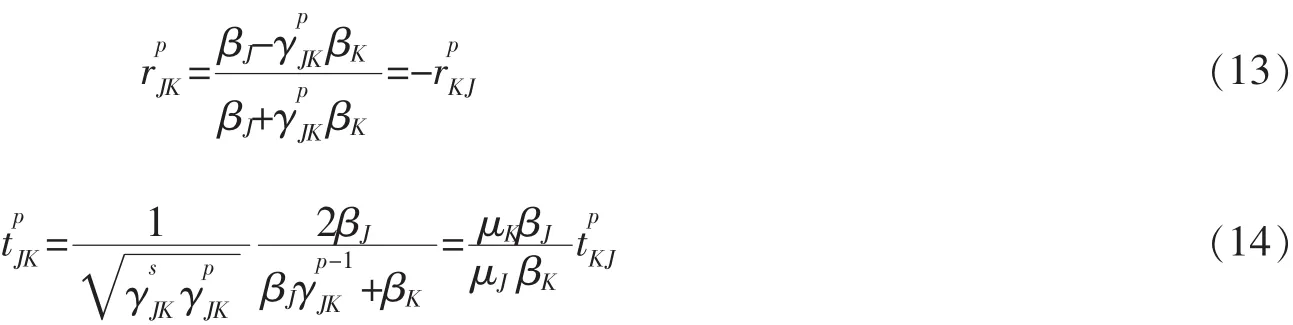
值得一提的是，由于（6）、（9）两式不涉及具体的介质信息，所以菲涅尔系数可以不依赖于中间层介质的选择和相关参数设定，具有一定的通用性。由于这种方法在计算某些多层介质结构（如多层周期型结构、含缺陷层结构等）时特别方便，可以将这些定义关系用于描述电磁波在局域、非局域、不均匀以及非具体的介质层组成的多层膜系统传播的情况。但是，如果电磁波入射到J层介质后经过的中间层不是K层，而是介于K层和M层之间的某一中间层L层，那么只有证明在这两种情况下电磁波从M层介质出射后的菲涅尔系数是一样时，才可以说这种递推关系具有前后一致性（rJ/K/M=rJ/L/M和tJ/K/M=tJ/L/M），即只要从J层入射和从M层介质出射，不管这两层介质之间所含是一层还是多层介质，都可得到一样的菲涅尔系数（rJ/M=rJ/K/M=rJ/L/M和tJ/M=tJ/K/M= tJ/L/M）。

2　多层介质膜的菲涅尔系数的等价性证明

下面，从理论上证明这种等价的合理性。首先，为了证明，将（6）式改写成下列形式：

由于 L层是介于 K层和 M 层之间的某一中间层，参照（16）式，反射系数可以表示为 rK/M=rK/L/M=其中aK/L=aL/K=tK/LtL/K-rK/LrL/K）。经过重新排列，结合（16）式，计算得到反射系数rJ/L和rL/J，进而得到

注意到，这里只要使bJ/L=aJ/L等式成立即可完成等价性的证明。于是，结合（9）、（16）两式，可得

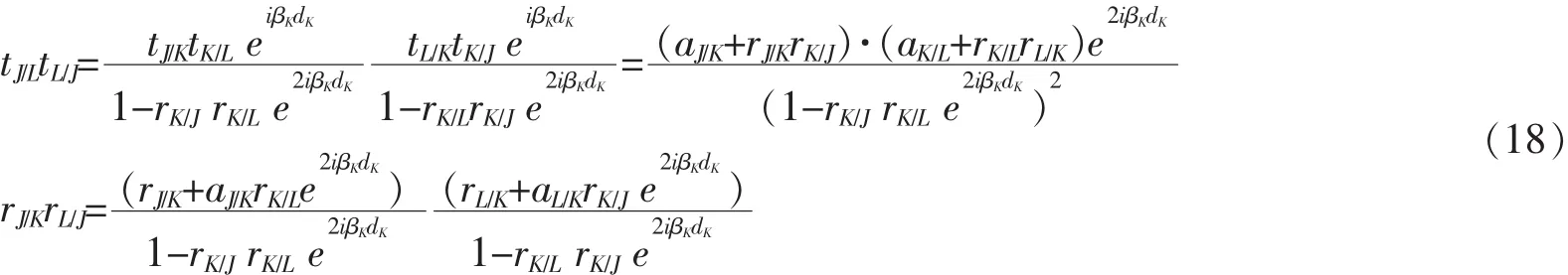
经过化简，得到

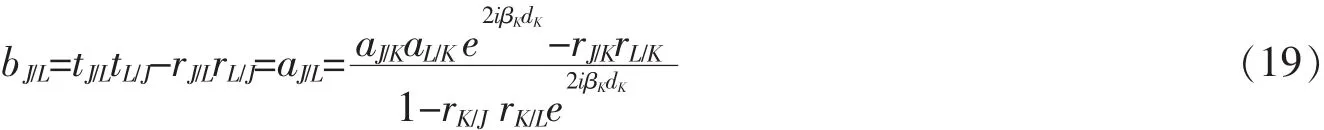
综上所述，反射系数rJ/M=rJ/K/M=rJ/L/M表达式成立。

同样地，可以证明透射系数的等价性tJ/M=tJ/K/M=tJ/L/M。结合和（rL/J－rL/K）（1-rK/LrK/Je2iβKdK），可得

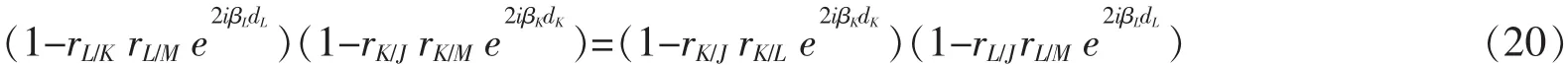
进行替换，可得

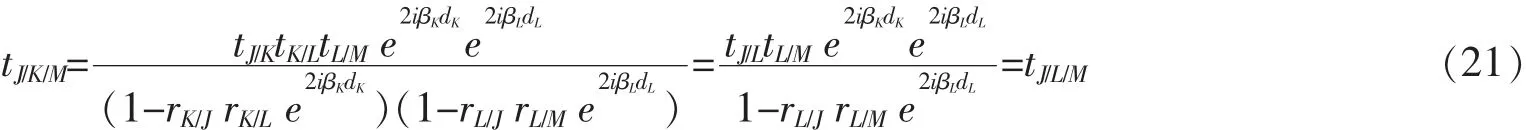
综上所述证明，经过不同中间介质层后的菲涅尔系数中透射系数具有等价性。

由于单界面的透射系数具有对称性，如（12）和（14）两式，这表明多层局域介质系统的透射系数也具有相类似的对称关系［2，9］

事实上，由两个单界面（J-K和K-M）透射系数（tJK和tKM）的对称性和（9）式可知，三层（J-K-M）介质系统的透射系数也是满足对称性的。假设在（9）式中，菲涅尔系数（tJ/K和tK/M）具有相同的对称性，（22）式也是成立的。

通过归纳推导过程可知，这个方程对于局域分层系统是普遍有效的。需要进一步说明，由于电磁波未说明一定要从哪个方向通过多层介质膜，这实际上就保证了通过该多层介质系统的透射系数是具有等价性的，因此，（22）式也可以适用的。

以此类推，将这个递推关系推广到无数多层的情况，就可以不依赖于具体介质信息，求解多层结构介质膜的菲涅尔系数（反射系数和透射系数）。

3　结语

笔者从理论上对电磁波在多层介质膜中传播时的菲涅尔系数（反射系数和透射系数）进行分析和推导，将其写成一个简单紧凑的递推关系以避免类似原有教材中出现繁琐冗长的多项式，并证明电磁波不管经过多少层中间介质，都可以统一成一个简单的递推关系。递推关系的方法大大简化了教材中的多项式结果，也不同于较难理解和掌握的转移矩阵法，是求解在多层介质膜中传播时的菲涅尔系数的一种行之有效的方法。

［1］BORN M，WOLF E.Principles of Optics［M］.New York：Pergamon，1980.

［2］CHEW W C.Waves and Fields in Inhomogeneous Media［M］.New York：IEEE，1995.

［3］CHEN X，WANG L G，LI C F.Transmission gap，Bragg-like reflection，and Goos-Hänchen shifts near the Dirac point inside a negative-zero-positive index metamaterial slab［J］.Phys Rev A，2009，80：043839.

［4］XU G D，XIAO Y T，LI J，et al.Imbert-Fedorov shifts of a Gaussian beam reflected from uniaxially anisotropic chiral media［J］.Ann Phys，2013，335：33-46.

［5］REED C E，GIERGIEL J，HEMMINGER J C，et al.Dipole radiation in a multilayer geometry［J］.Phys Rev B，1987，36：4990-5000.

［6］CRAWFORD O H.Radiation from oscillating dipoles embedded in a layered system［J］.J Chem Phys，1988，89：6017-6027.

［7］FORD G W，WEBER W H.Tip-substrate interaction in optical near-field microscopy［J］.Phys Rep，1984，113：195-287.

［8］MARTINI F D E，MARROCCO M，MATALONI P，et al.Spontaneous emission in the optical microscopic cavity［J］.Phys Rev A，1991，43：2480-2497.

［9］TOMAŠ M S.Green function for multilayers light scattering in planar cavities［J］.Phys Rev A，1995，51：2545-2529.

［10］ZHOU F，SPRUCH L.Van der Waals and retardation（Casimir）interactions of an electron or an atom with multilayered walls［J］.Phys Rev A，1995，52：297-310.

［11］TOMAŠ M S.Casimir force in absorbing multilayers［J］.Phys Rev A，2002，66：052103.

［12］SUN J，HUA X K，GONCHARENKO A V，et al.Casimir force between composite materials containing nonspherical particles［J］.Phys Rev A，2013，87：042509.

［13］SUN J，HUANG Y，GAO L.Nonlocal composite media in calculations of the Casimir force［J］.Phys Rev A，2014，89：012508.

［14］VIGOUREUX J M.Use of Einstein's addition law in studies of reflection by stratified planar structures［J］.J Opt Soc Am A，1992，9：1313-1319.

［15］VIGOUREUX J M，GIUST R.Explicit Stokes reciprocity relations for plane stratified media［J］.Opt Commun，2000，176：1-8.

［16］BERREMAN D W.Optics in stratified and anisotropic media：4×4-matrix formulation［J］.J Opt Soc Am，1972，62（4）：502-510.

责任编辑：李文杰

Derivation of the Fresnel coefficients in multi-layered dielectric film by recursive relations

SUN Jian1，XU Yaoxian2，TANG Lili3
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Oversea Education，Nanjing U-niversity of Posts and Telecommunications，Nanjing 210023，China；3.School of Electronic&Information Engineering，SUST，Suzhou 215009，China）

We have investigated the Fresnel coefficients in multi-layered dielectric film by recursion relations. The Fresnel coefficients（reflection coefficients and transmission coefficients）of the electromagnetic wave propagating in multi-layered dielectric film were theoretically analyzed and deduced.They were written in a simple compact form with recursion relations in order to avoid the tedious and lengthy polynomials shown in the textbooks.The results show that the Fresnel coefficients of the electromagnetic wave propagating through arbitrary multiple layers can be unified to a simple recursive formula.

Fresnel coefficients；recursive relations；reflection coefficients；transmission coefficients；multi-layered dielectric film

O441

A

1672-0687（2016）03-0022-05

2015-09-09

江苏省青年基金项目（BK20130284）；江苏省高校自然科学研究项目（13KJB140017）；苏州科技学院自然科研基金项目（XKZ201403）；苏州科技学院天平学院教育教学改革研究项目（2015TJGB-09）；苏州科技学院2015年科研启动项目

孙坚（1978-），男，江苏苏州人，副教授，博士，研究方向：凝聚态物理。