北京市大兴新城水源地保护区划分

陈 瑾，周瑞静，黄 栋，张 雪（. 北京市地质工程勘察院，北京 00048；. 北京市地质矿产勘查开发局信息中心，北京 0095）

北京市大兴新城水源地保护区划分

陈 瑾1，周瑞静1，黄 栋1，张 雪2
（1. 北京市地质工程勘察院，北京 100048；2. 北京市地质矿产勘查开发局信息中心，北京 100195）

北京地下水资源持续超采，已出现水资源枯竭和浅层地下水大面积污染问题，建立饮用水源地保护区是保护地下水水源的有效手段。本文应用数值模拟法和公式法，对北京大兴新城水源地保护区进行划分。考虑大兴水厂所在地水文地质条件，分别对第四系和基岩进行保护区划分，对不同分区进行叠加，得出水源地保护区范围。通过两种方法计算出的保护区面积相差不大，但是数值模拟法计算出的二级保护区面积比公式法计算的结果小5.5km2，主要因为公式法计算时没有考虑地下水含水层边界条件和岩溶地下水富水性不均一等因素，而数值模拟模型在水文地质条件的基础上进行水源地保护区划分，比较符合水源地所在区域实际的水文地质条件。通过对划分结果的对比和分析可以看出，公式法划分水源保护区的方法简便易行，但是概化结果与实际地质条件差异较大。数值模拟法对含水层结构和水文地质条件的概化相对客观、详尽，但是该法应用过程较复杂。在实际划分水源保护区的工作中，应将公式法和数值模拟法结合应用。

水源地保护区划分；公式法；数值模拟法

0　前言

水源地保护区是指为防止水源地（多为饮用水）污染、保护水源地环境质量而划定并要求加以特殊保护的一定面积的水域和陆域，它分为地表和地下水饮用水水源地保护区（国家环境保护总局，2007）。地下水资源是北京供水系统的支柱，但随着城市的日益扩大、人口的急剧增长，北京的地下水资源因为持续超采，已经出现水资源枯竭和浅层地下水大面积污染的问题。水源地的采水安全是关系到北京城市供水安全的重要保障，而建立饮用水源地保护区则是保护地下水水源的有效手段（李建新，2000）。

在地下水水源地保护区划分的过程中，应综合考虑水源地所处的地理位置、井源类型、供水数量开采方式、水文地质条件和周边污染源分布（徐海珍等，2009；陈学林等，2013）。《饮用水水源保护区划分技术规范》中提出可以根据水源地日供水能力区分，选择数值模拟法或公式法对地下水水源地保护区进行划分。本文分别用数值模拟法和公式法两种方法，对北京大兴新城一二水厂水源地保护区进行了划分。

1　地下水源地保护区划分方法

1.1公式法概述

该法通过选取水源地水源井所在地的代表性水文地质参数，按公式（1），经计算得到水力半径，再结合水源地水源井所在处的地形地貌、行政分区等，对保护区形状作适当调整，确定保护区的最终范围。即在对水源地保护区进行划分中以取水井为中心，根据取水井周边水力梯度、渗透系数等水文地质条件，计算出水流质点沿水流方向迁移100d的距离为半径所划定的圆为一级保护区；一级保护区以外，水流质点沿水流方向迁移1000d的距离为半径所划定的圆为二级保护区；划定水源地的补给区和径流区为准保护区（国家环境保护总局，2007；赵红梅等，2013）。

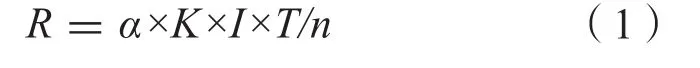
式中：

R——保护区半径（m）；

α——安全系数，一般取2；

I——水力坡度，本次实例中孔隙水统一取0.72‰，基岩裂隙水统一取0.6‰；

K——取水层的含水层侧向渗透系数（m/d），本次实例中孔隙水取值80m/d，基岩裂隙水取值76m/d；

T——质点水平运移时间（d），一级保护区、二级保护区质点水平运移时间分别对应100d和1000d；

n——有效孔隙度，根据本次实例水源地的地质条件，取值0.15。

1.2数值模拟法概述

数值模拟法是根据研究区的地质条件、地下水位、地层空间结构、边界与源汇项以及其它水文地质条件，对研究区的水文地质条件进行概化，建立起研究区的概念模型和数学模型，运用地下水数值模拟软件，对研究区的水文地质条件进行识别和验证，使模型尽量贴合实际的水文地质条件参数（王金生等，2004；王澎，2003）。进一步运行模型，分别求得质点运行100d和1000d的距离，以水流质点运移100d的距离为半径所划定的圆为一级保护区；一级保护区以外，水流质点运移1000d的距离为半径所划定的圆为二级保护区；人为划定水源地的补给区和径流区为准保护区。分别计算得到不同取水层水源井一级保护区和二级保护区半径后，综合考虑水源地所处的地理位置、井源类型、供水数量开采方式、水文地质条件和周边污染源分布，划定水源地各级保护区的范围（赵红梅等，2013）。

2　大兴新城水源地保护区划分

2.1水源地概况

大兴新城水源地位于北京大兴区，水源地供水井44眼，分为第四系井和基岩井，总计开采量为1200～1500×104m3/a（北京市地质工程勘察院，2009）。

大兴水厂所在地第四系沉积厚度各地分布不均一，西北向东南逐渐加厚。第四系含水层岩性西北为单一的砂砾石层，向东南颗粒逐渐变细，以中细砂层为主。含水层富水性大小与含水层岩性、厚度密切相关，自西北向东南单井水位下降5m时，涌水量从大于5000m3/d下降到1500～3000m3/d。地下水的补给主要来源大气降水入渗补给、上游的侧向补给以及灌溉水的回归和地表水等的入渗补给，地下水自西北向东南径流。

基岩含水岩组主要是奥陶系和寒武系岩溶裂隙含水岩组，分布在研究区中心地带，顶板埋深约80m，向上与第四系直接接触，基岩顶部普遍有10～12m的粘性土层。奥陶系岩溶裂隙水含水岩组是本区主要开采层。岩性以白云质灰岩为主，夹有灰岩和白云岩。地层岩溶裂隙发育，富水条件好，降深在0.45～7m时，单井出水量为1200～5000m3/d，是本区富水性最好的含水岩组。寒武系岩溶裂隙水含水岩组岩性为鲕状灰岩、豹斑状泥晶灰岩，该含水岩组岩溶裂隙发育，富水性较好，降深在2～30m时，单井出水量为800～1400m3/d。

2.2公式法

（1）第四系地下水

一级保护区的保护半径：R = 200% ×80×0.72‰×100/0.15 = 76.8m；

二级保护区的保护半径：R = 200% ×80×0.72‰×1000/0.15 = 768m。

通过计算：一级保护区半径为76.8m，面积为0.23km2；二级保护区半径为768m，面积为34.36km2；一、二保护区面积共计：34.59km2。

（2）岩溶地下水

一级保护区的保护半径：R = 200% ×76×0.6‰×100/0.15 = 60.8m；

二级保护区的保护半径：R = 200% ×76×0.6‰×1000/0.15 = 608m。

通过计算：一级保护区半径为60.8m，面积为0.42km2；二级保护区半径为608m，面积为：50.46km2；一、二保护区面积共计：50.88km2。

（3）大兴新城地下水水源地保护区

通过以上分别对第四系和基岩进行保护区划分，对不同分区进行叠加，得出水源地保护区范围：一级保护区面积为0.51km2，二级保护区面积为58.00km2，准保护区面积为41.89km2，面积共计100.4km2（图1）。

2.3数值模拟法

（1）模拟区概况

模拟区范围以大兴新城一、二水厂水源井为中心，西部以永定河为边界，南部以西庄村为界，东至旧宫镇，北至黄土岗村，模拟面积252.8km2。

（2）地下水系统概念模型

依据地质和水文地质条件，模型在空间上分为3层，第一含水层组（第四系含水层）、弱透水层和第二含水层组（基岩裂隙含水层）。模拟区地下水系统的概念模型概化成非均质各向异性、空间三维结构、非稳定地下水流系统（张立志，2009；李星宇等，2014）。

（3）地下水系统数学模型

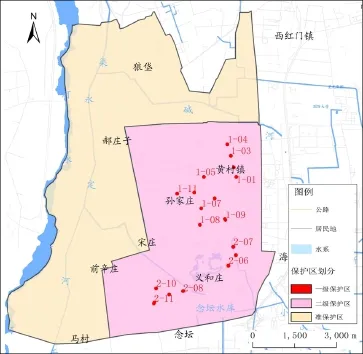
图1　公式法确定水源地保护区划分图Fig.1 Formula method to determine the delineating water source protection areas map

建立地下水水流模型，采用不规则三角剖分，水源井在剖分时自动加密，剖分后的模拟区共108704个结点，162342个单元格。采用2006年1月统测的地下水水位作为初始水位，模拟时期为2006年1月到2008年12月，以一个月作为一个时间段。通过模拟期末（2008年12月30日）含水层的模拟流场与实际流场对比图（图2）可知，所建立的模拟模型基本达到模型精度要求，符合研究区实际水文地质条件，基本反映了地下水系统的动态特征，故可利用模型来确定水源地一级保护区和二级保护区。

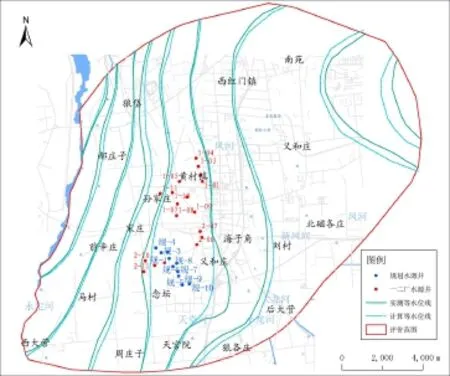
图2　实测水位等值线与计算水位等值线对比图Fig.2 Study on measured water level and calculated water level comparison map

（4）第四系保护区

通过模拟模型计算得出：质点在第四系含水层运行100d的距离为72m，运行1000d的距离为675m，得出一级保护区面积为0.29km2，二级保护区面积为27.91km2，准保护区面积为47.39km2，共计75.59km2。

（5）基岩保护区

通过模拟模型计算得出：质点在第四系含水层运行100d的距离为64m，运行1000d的距离为620m，得出水源地一级保护区面积为422m2，二级保护区面积为52.383km2，共计52.80km2。

（6）大兴新城地下水水源地保护区

通过以上分别对第四系和基岩进行保护区划分，对不同分区进行叠加，得出水源地保护区范围：一级保护区面积为0.54km2，二级保护区面积为52.50km2，准保护区面积为47.83km2，共计100.87km2（图3）。

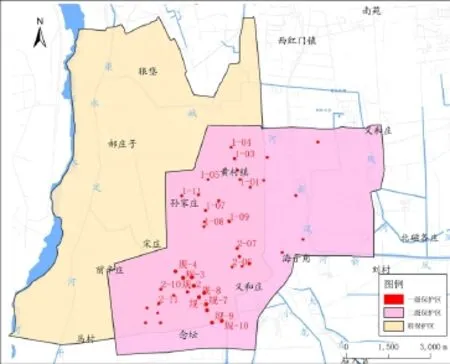
图3　数值模拟模型确定水源地保护区划分图Fig.3 Numerical simulation method to determine the delineating water source protection areas map

2.4结果分析

通过以上两种方法，求得保护区的面积相差不大。虽然数值模拟计算的总面积小于数值公式法计算出的总面积，但是数值模拟计算出的二级保护区面积比公式法计算的结果小5.5km2，主要因为公式法计算时没有考虑地下水含水层边界条件和岩溶地下水富水性不均一等因素；而数值模拟模型在水文地质条件的基础上进行水源地保护区划分，比较符合水源地所在区域实际的水文地质条件，本研究认为数值模拟法计算得到的保护区范围比公式法计算结果更为合理，因此，本研究结果采用数值模拟法计算的范围。

3　结论

通过对划分结果的对比和分析可以看出，公式法划分水源保护区的方法简便易行，但是主观性较强，而且概化结果与实际地质条件差异较大，常出现划定区域保护强度过高或过低的现象。

数值模拟法对含水层结构和水文地质条件的概化相对客观、详尽，适用于各种背景的水源地研究，尤其对于大型地下水源地保护区的划分，水源保护区划分结果比较可靠、准确，但是该法应用过程较复杂，所需条件多，工作量大，特别对于复杂水文地质条件的水源地，概化时也会产生一定的误差。

由此可见，数值模拟法可以弥补公式法刻画含水层结构和水文地质条件不够准确的缺陷，而公式法划分结果又可以对区域水文地质条件做出一定的控制参考，以避免模型调参时出现脱离实际偏差太大的后果。在实际划分水源保护区的工作中，应将公式法和数值模拟法结合应用，才能使地下水水源地保护区的划分结果准确、可靠。

［1］国家环境保护总局. 饮用水水源保护区划分技术规范（HJ/T 338-2007） ［S］. 2007.

［2］赵红梅，肖杰. 公式法与数值模拟法在地下水饮用水源保护区划分中的应用——成都平原某水源地为例［J］. 四川环境，2013，32：60～64.

［3］李建新. 我国生活饮用水水源保护区问题的探讨［J］. 水资源保护，2000，3：12～14.

［4］徐海珍，李国敏，张寿全，等. 地下水水源地保护区划分方法研究综述［J］. 水利水电科技进展，2009，29（2）：80～82.

［5］陈学林，胡兴林，王双合，等. 地下水饮用水水源地保护区划分关键技术研究［J］. 水文，2013，33（6）：69～71.

［6］王金生，王澎，刘文臣. 划分地下水源地保护区的数值模拟方法［J］. 水文地质工程地质，2004，4：83～86.

［7］王澎. 用数值模拟的方法划分地下水水源地保护区［J］. 山西焦煤科技，2003，6（增刊）：10～12.

［8］北京市地质工程勘察院. 北京市大兴新城一二水厂地下水源地保护区重新划分技术报告［R］. 2009.

［9］张立志. 基于FEFLOW的大兴区地下水动态模拟研究［D］. 北京：中国地质大学（北京），2009.

［10］李星宇，南天，王新娟，等. 数值模拟方法在隐伏岩溶水源地保护区划分及污染治理中的应用［J］. 中国岩溶，2014，33（3）：280～286.

Delineation of Groundwater Source Protection Area in Beijng Daxing New Town

CHEN Jin1， ZHOU Ruijing1， HUANG Dong1， ZHANG Xue2
（1.Beijing Institute of Geological & Prospecting Engineering， Beijing 100048； 2. The Information Center， Beijing Geology Prospecting & Developing Bureau， Beijing 100048）

Because the groundwater resources in Beijing are sustained overdraft， there have been the problems of water resource depletion and shallow layer groundwater contaminated in large areas. It is an effective way to establish the protection area of drinking water to protect the groundwater source. In this paper， we use the numerical simulation and formula method in the delineation of Beijing Daxing new town waterworks protection areas. Considering the hydrogeological conditions of the Daxing waterworks， the scope of the protection area is obtained through delineation of Quaternary and basement rocks respectively and superposition of different partitions. There is little difference in the calculation by two methods， but the area calculated by the numerical simulation method is smaller 5.5km2than that of the formula method. The main reason is that the groundwater aquifer boundary conditions and inhomogeneity of watery in karst underground water are not considered by formula method. Based on the hydrogeological conditions， the numerical simulation model is delineated， which is quite consistent with the actual hydrogeological conditions in the local area. Through the comparison and analysis of the results， the formula method is simple， but the generalization of the geological conditions is very different from the actual geological conditions. The numerical simulation method can generalize the aquifer structure and hydrogeological conditions more exhaustive and objective， and the division result of protection areas may be more reliable and accurate. But the application of numerical simulation method is more complex and workload. The formula method should be combined with the numerical simulation method in the application.

Daxing new town； Formula method； Numerical simulation method

X523

A

1007-1903（2016）01-0089-05

10.3969/j.issn.1007-1903.2016.01.018

陈瑾（1983- ），女，工程师，主要从事环境地质。E-mail：ccjjhb@163.com。