基于申请通行记录的桥梁超限车辆荷载统计模型

符献民， 谢上飞， 何慧中， 晏班夫

(1.湖南大学 土木工程学院， 湖南 长沙　410082；　2.湖南省交通科学研究院， 湖南 长沙　410015)



基于申请通行记录的桥梁超限车辆荷载统计模型

符献民1， 谢上飞2， 何慧中1， 晏班夫1

(1.湖南大学 土木工程学院， 湖南 长沙410082；2.湖南省交通科学研究院， 湖南 长沙410015)

根据广西区申请通行的超限车辆数据信息，基于概率统计理论，采用双峰正态分布和对数正态分布建立了该区五轴和六轴超限车辆总重和轴距的概率分布模型；根据一元正态线性回归理论，建立了总重与轴重的线性回归模型；分析了超限车辆总重和轴距之间的相互关系。根据建立的超限车辆荷载模型，采用蒙特卡洛(Monte Carlo)法各随机生成了10000辆五轴、六轴超限车辆，通过对比随机生成的超限车辆与实际超限车辆对中小跨径简支梁桥产生的跨中最大弯矩效应，验证了按照本文方法建立的超限车辆荷载模型用以模拟实际超限车辆的可行性，同时也为五轴、六轴超限车辆过桥时桥梁的安全评估提供了基础数据。

超限车辆； 车辆荷载模型； 概率统计模型； 线性回归； 随机生成

0　引言

目前国内对超重、超限车辆的管理主要是通过行政罚款，不能从根本上解决超载运输对桥梁结构的非正常损伤甚至桥梁垮塌等问题[1]。

国外对超限车辆过桥的安全评估研究相对较早，有系统的规范条文[2]验算超车车辆过桥时桥梁的安全性；Jian Zhao等[3]通过拟合超重车辆过桥的荷载效应比，给出了五轴车的荷载模型；Gongkang Fu等[4]基于概率统计理论，建立了包含超重车辆在内的车辆总重概率模型；César CrespoMinguillbón等[5]对超重车辆的总重分布模型进行了研究，给出了超重车辆总重和轴重的相关系数矩阵；文献[6-11]基于实测的车辆数据，建立了车辆总重、轴重、轴距等轮轴特征参数的多峰分布概率模型。

以上对车辆荷载模型的研究，侧重于研究车辆的总重、轴重以及轴距等轮轴特征参数各自的概率分布类型。本文则根据广西区超限运输车辆申请通行表数据，研究了车辆总重、轴重和轴距等轮轴特征参数之间的相互关系，基于概率统计理论，建立了超限车辆的荷载模型，通过比对中小跨径简支梁桥的跨中最大弯矩效应，验证了按照本文建立的超限车辆荷载模型的可行性。

1　超限车辆数据的采集

超限运输车辆的逐年增加，使得广西区道路行政管理部门审批超限运输车辆通行的工作量大大增加。依托该区公路管理局提供的超限运输车辆申请通行表数据，可知从2009年至2013年申请通行的超限车辆多达800多辆，车型从四轴车到十四轴车不等，其中又以五轴和六轴超限车辆居多(见表1)，本文重点研究五轴和六轴超限车辆的轮轴特性。

表1 超限车辆数据Table1 Datarecordsofoverloadedvehicle车辆类型车辆数车辆类型车辆数四轴车9十轴车 18五轴车172十一轴车16六轴车531十二轴车4七轴车37十三轴车3八轴车15十四轴车6九轴车22

2　超限车辆荷载模型

超限车辆对桥梁结构产生的荷载效应不仅与总重有关，还与轴重及轴距等轮轴特征参数有关。不同轮轴特征参数使得超限车辆荷载变得更加复杂。

根据主车和挂车的相对位置，把主车的前轴作为车辆的第一轴，依次排列下去，分别为第二、三、四、五、六轴等。基于上述排序原则，作者对某区申请通行的五轴、六轴超限车辆的总重、轴重和轴距等轮轴特征参数进行了详细的概率统计研究，建立了该区五轴、六轴超限车辆的荷载模型。

2.1总重概率模型

申请通行的五轴、六轴超限车辆均以半挂车为主。其中五轴超限车辆的总重分布在294～980 kN之间，且以490 kN和790 kN居多；六轴超限车辆的总重分布在320～1225 kN之间，且以539 kN和784 kN居多。从原始数据可以看出，五轴、六轴超限车辆的总重均呈现出双峰型的概率分布模式。

基于非线性最小二乘法的基本原理，采用Levenberg-Marquardt[12]算法，对五、六轴超限车辆总重概率分布分别进行拟合，经K — S优度检验[13]，可知五、六轴超限车辆总重概率分布均不拒绝服从双峰正态分布，且拟合效果较好。五轴、六轴超限车辆总重截口分布的概率密度函数表达式可统一表示为：

式中：μ1、σ1、ω1、μ2、σ2、ω2分别是第1个、第2个正态分布的均值、标准差和权重系数，其中ω2=1-ω2；xmin和xmax分别为超限车辆总重的最小值和最大值；k是截口分布的正规化常数，即：

(2)

式中： 五轴超限车辆的xmin和xmax分别为294 kN和980 kN；六轴超限车辆的xmin和xmax分别为320 kN和1225 kN。

将式(2)经过积分变换后可转化为下式：

(3)

式中：Φ(x)是标准正态分布的累积分布函数；tmax1=(xmax-μ1)/σ1；tmin1=(xmin-μ1)/σ1；tmax2=(xmax-μ2)/σ2；tmin2=(xmin-μ2)/σ2。

图1给出五轴、六轴车总重截口分布的概率分布拟合曲线，拟合的分布参数见表2。

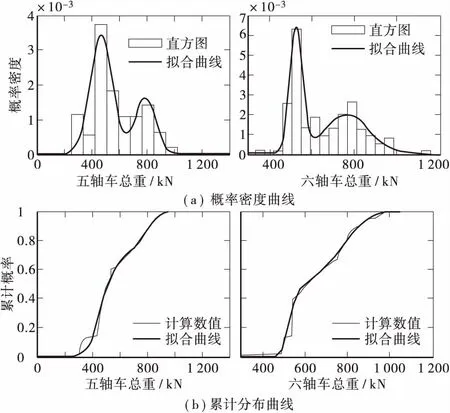
图1　概率分布曲线拟合图Figure 1　Fitting curve of probabilistic distribution

2.2轴重与总重的线性回归模型

统计发现，广西区五轴、六轴超限车的总重与各轴轴重之间存在一定的相关关系。根据总重和轴重原始数据，采用一元正态线性回归[14]理论建立了五轴、六轴超限车总重和轴重的一元线性回归模型。图2仅给出部分线性回归图，具体回归参数见表3。

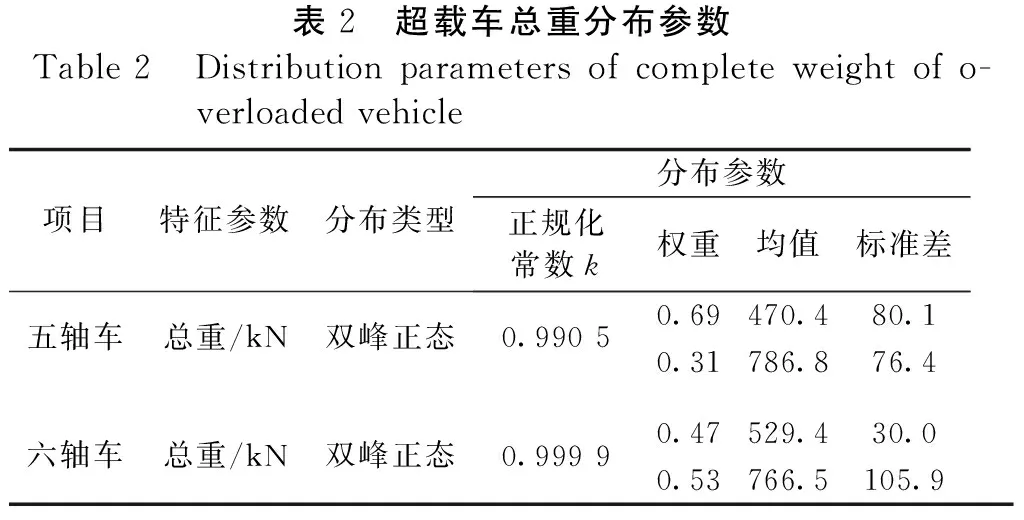
表2 超载车总重分布参数Table2 Distributionparametersofcompleteweightofo-verloadedvehicle项目特征参数分布类型分布参数正规化常数k权重均值标准差五轴车总重/kN双峰正态0.99050.69470.480.10.31786.876.4六轴车总重/kN双峰正态0.99990.47529.430.00.53766.5105.9

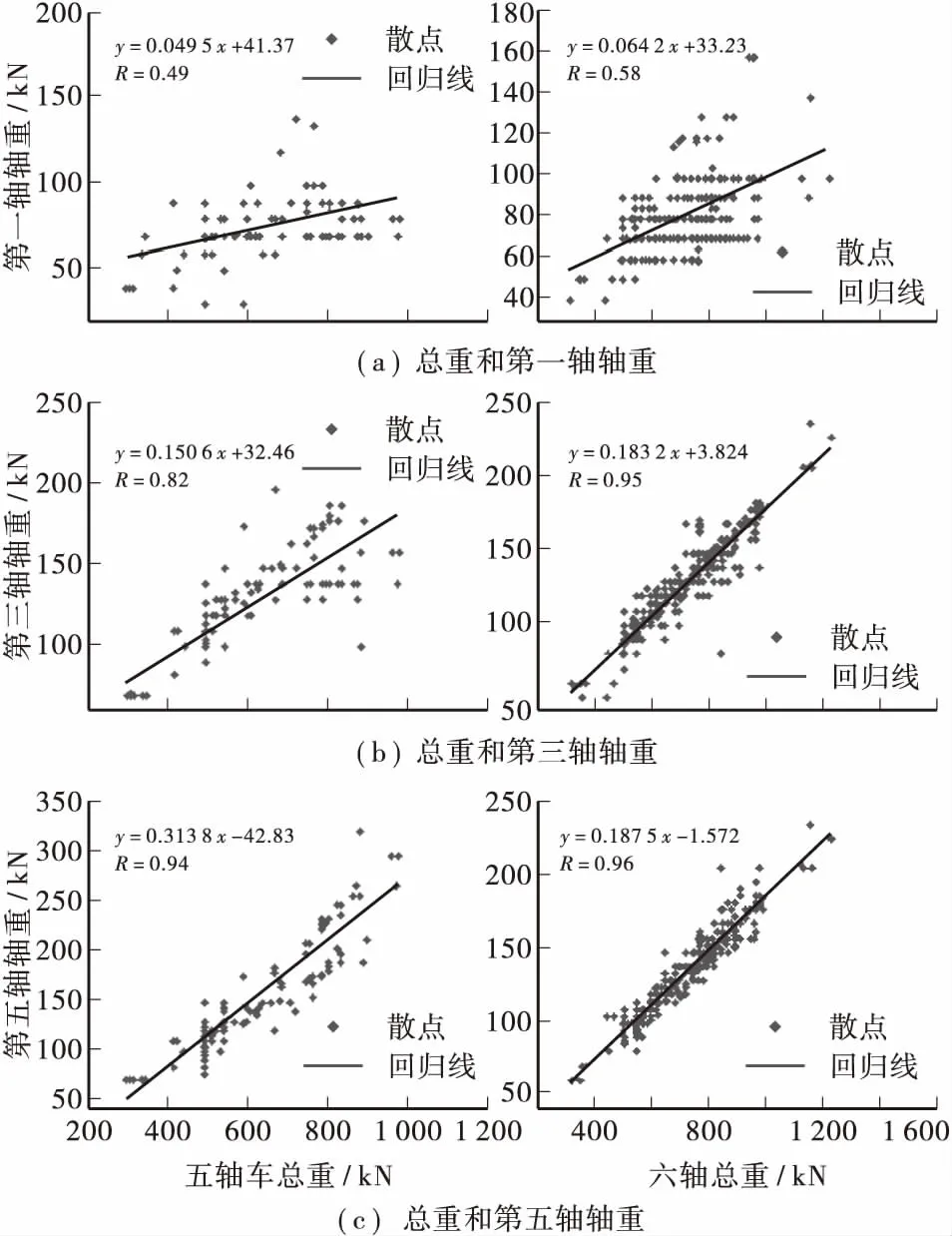
图2　超限车辆总重和轴重的线性回归图Figure 2　　　　Linear regression of the complete weight and axle weight of the overloaded vehicle

从上述线性回归图和相关系数指标可以看出，五轴、六轴超限车辆除各自的第一轴的轴重外，其余各轴的轴重和总重之间具有良好的线性相关性。故五轴、六轴超限车辆除第一轴的轴重外，其余各轴轴重可以根据总重按照线性回归方程推算，而第一轴的轴重则按照总重减去其余各轴轴重和进行计算。

2.3五轴超限车轴距的概率模型

广西区典型的五轴超限车辆有两种类型(见图3)。用L1表示联轴的轴间距，L3表示主车和挂车之间的轴间距，L2表示其它相邻轴的轴间距。

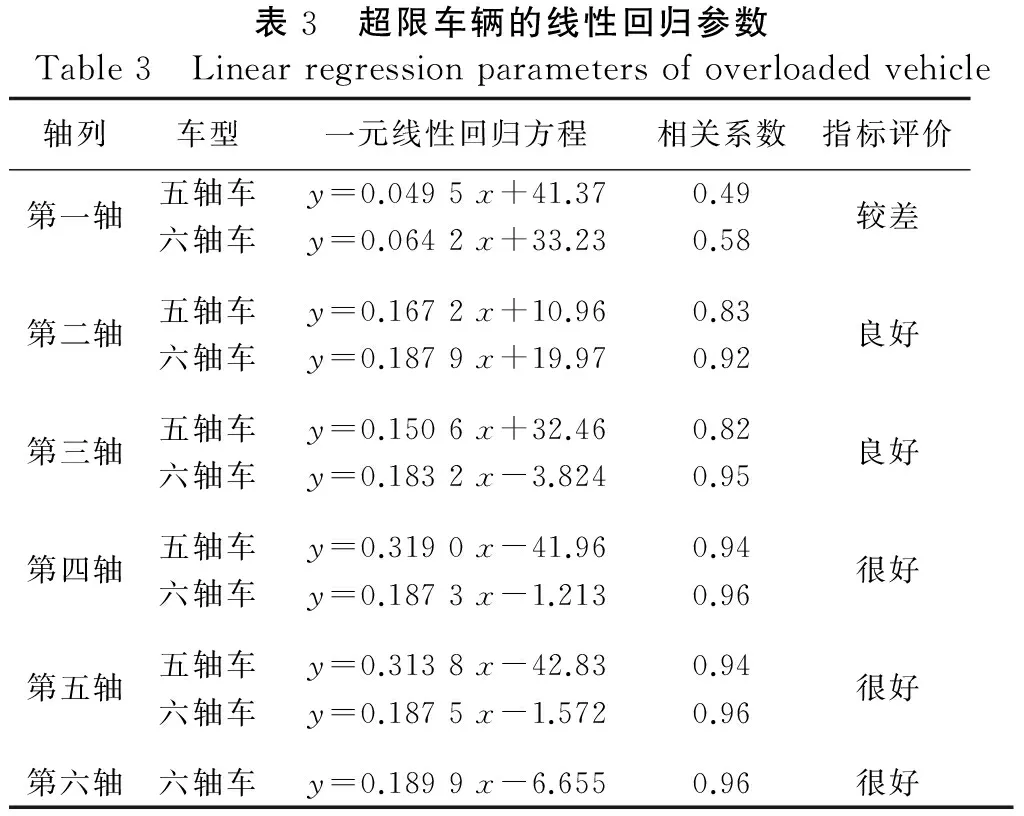
表3 超限车辆的线性回归参数Table3 Linearregressionparametersofoverloadedvehicle轴列车型一元线性回归方程相关系数指标评价第一轴五轴车y=0.0495x+41.370.49较差六轴车y=0.0642x+33.230.58第二轴五轴车y=0.1672x+10.960.83良好六轴车y=0.1879x+19.970.92第三轴五轴车y=0.1506x+32.460.82良好六轴车y=0.1832x-3.8240.95第四轴五轴车y=0.3190x-41.960.94很好六轴车y=0.1873x-1.2130.96第五轴五轴车y=0.3138x-42.830.94很好六轴车y=0.1875x-1.5720.96第六轴六轴车y=0.1899x-6.6550.96很好

图3　典型五轴超限车辆图Figure 3　Typical overloaded vehicle with 5 axles

2.3.1轴距L1和L2的分布特征

轴距数据显示，类型1超限车的后三轴为三联轴，第三轴和第四轴的轴距与第四轴和第五轴的轴距大小相同；类型2超限车的主车双联轴轴距与挂车双联轴轴距大小相同。对轴距L1、L2的原始数据进行统计分析，得到了轴距数值分布的柱状图(见图4)。

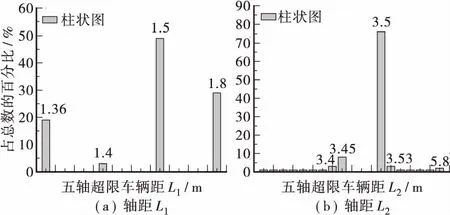
图4　轴距分布的柱状图Figure 4　Distribution histogram of axle base

由图4可知: 轴距L1主要集中分布在1.36、1.5和1.8 m共3个点，占总数的百分比为97%，故在模拟轴距L1的分布时按1.36、1.5和1.8 m共3个点所占的比例进行分配。

轴距L2主要集中分布在3.45 m和3.5 m两个点，占总数的百分比分别为8%和76%，其余数据点中，个数最多的占总数的百分比不到3.0%，由于3.45 m和3.5 m仅相差5 cm，可以忽略不计，且L2又以3.5 m占主导地位，故取轴距L2为3.5 m。

2.3.2轴距L3的概率模型

轴距L3分布在2.8～32.5 m范围之间，采用Levenberg-Marquardt算法，对轴距L3的概率分布进行拟合，经K — S优度检验，可得轴距L3的概率分布不拒绝双峰正态分布，且拟合效果较好。拟合的分布参数见表4，拟合的概率分布曲线见图5。

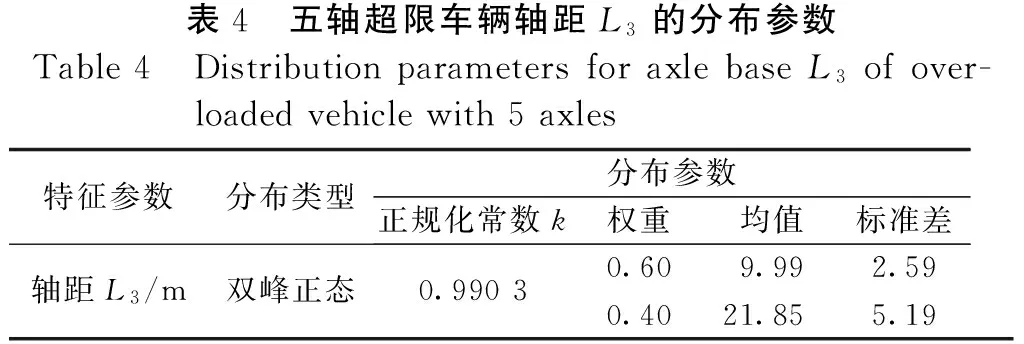
表4 五轴超限车辆轴距L3的分布参数Table4 DistributionparametersforaxlebaseL3ofover-loadedvehiclewith5axles特征参数分布类型分布参数正规化常数k权重均值标准差轴距L3/m双峰正态0.99030.609.992.590.4021.855.19

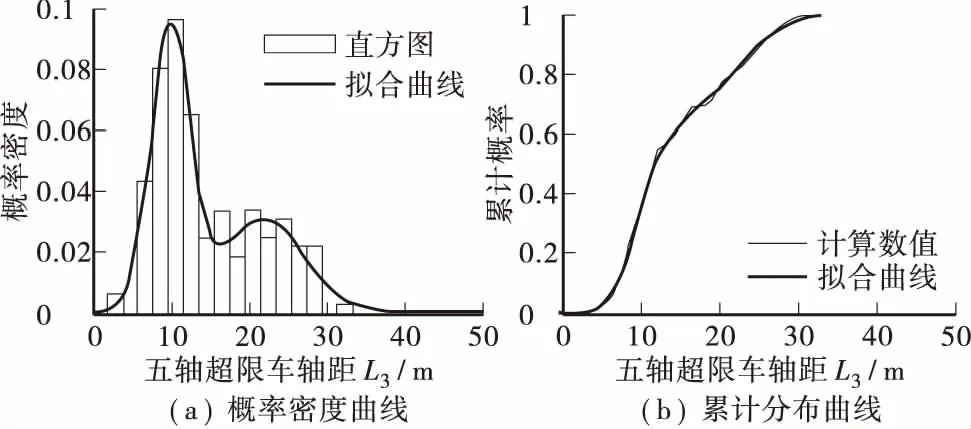
图5　概率分布曲线拟合图Figure 5　Fitting curve of probabilistic distribution

2.3.3轴距概率模型的建立

根据轴距L1的大小将图3所示的两类典型超限车各细分成3小类(见图6)。

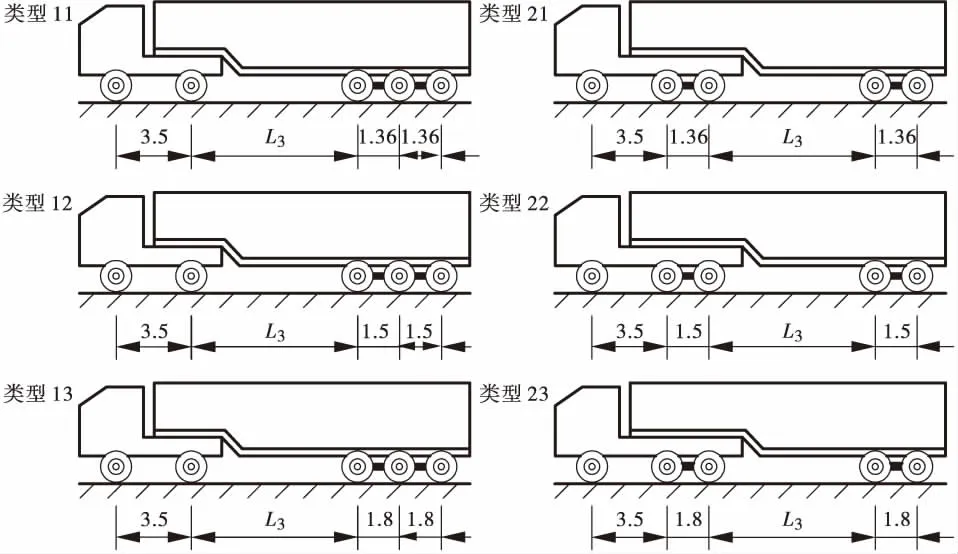
图6　5轴超限车辆按轴距大小分类图Figure 6　　　　Axle base-informed classification figure of the overloaded vehicle

轴距L3的数值在上述六小类超限车辆中均随机分布在2.8～32.5 m范围之间，因此按上述六小类超限车各自所占的比例和随机分配的轴距L3，即可建立五轴超限车轴距的概率模型，具体参数见表5。

2.4六轴超限车轴距的概率模型

广西地区典型的六轴超限车辆类型见图7，用L1Z表示主车联轴的轴间距，用L1G表示挂车联轴的轴间距，L3表示主车和挂车之间的轴间距，L2表示其它相邻轴的轴间距。

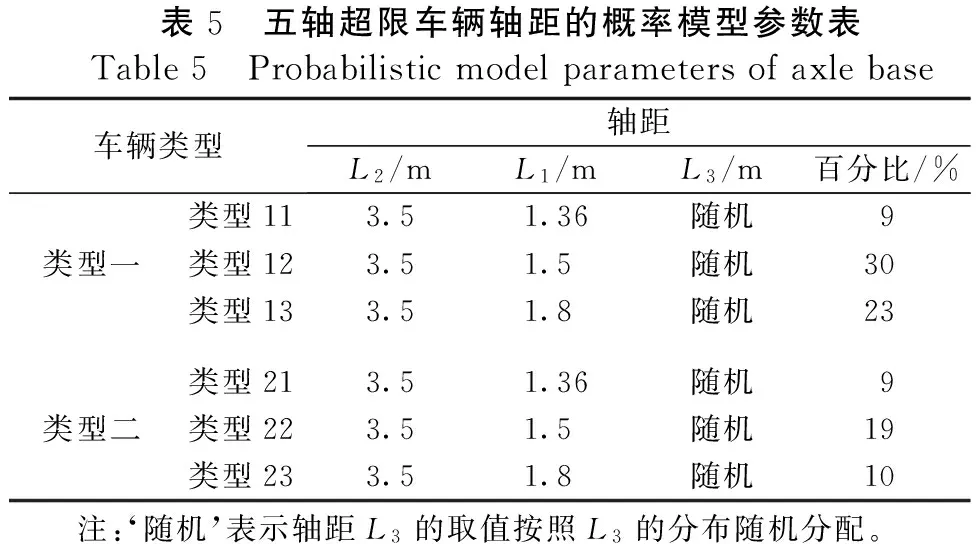
表5 五轴超限车辆轴距的概率模型参数表Table5 Probabilisticmodelparametersofaxlebase车辆类型轴距L2/mL1/mL3/m百分比/%类型113.51.36随机9类型一类型123.51.5随机30类型133.51.8随机23类型213.51.36随机9类型二类型223.51.5随机19类型233.51.8随机10 注:‘随机’表示轴距L3的取值按照L3的分布随机分配。

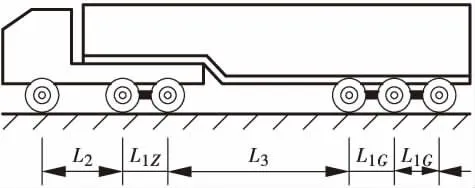
图7　典型六轴超限车辆图Figure 7　Typical overloaded vehicle with 6 axles

2.4.1轴距L1Z、L1G和L2的分布特征

轴距原始数据显示，六轴超限车辆的后三轴为三联轴，第四轴和第五轴的轴距与第五轴和第六轴的轴距大小相同。对轴距L1Z、L1G、L2的原始数据进行统计分析，得到了轴距数值分布的柱状图(见图8)。

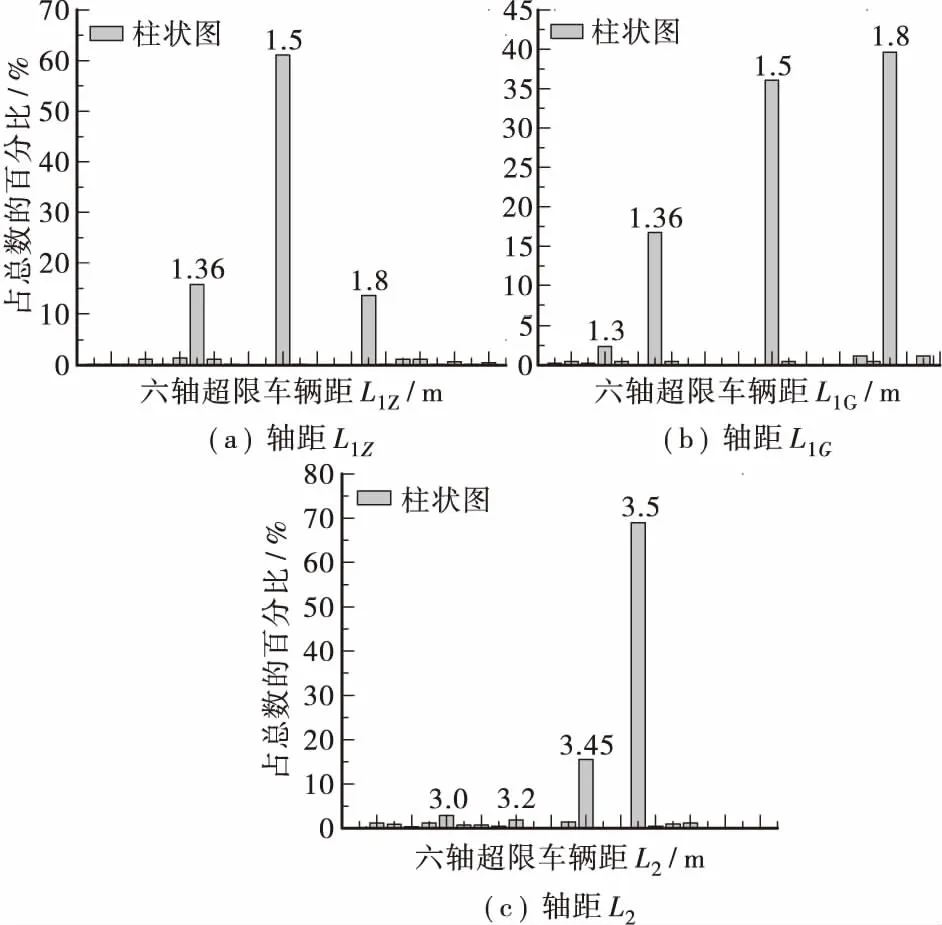
图8　轴距数值分布的柱状图Figure 8　Distribution histogram of axle base

由图8可知: 轴距L1Z和L1G主要集中分布在1.36、1.5，1.8 m共3个点，占总数百分比分别为91%和93%，其余数据点中，个数最多占总数的百分比均不到2.5%，故在模拟轴距L1Z和L1G的分布时按1.36、1.5，1.8 m共3个点所占比例进行分配。

轴距L2主要集中分布在3.45 m和3.5 m两个点，占总数的百分比分别为16%和69%，其余数据点中，个数最多的占总数的百分比不到3.0%，由于3.45 m和3.5 m仅相差5 cm，可以忽略不计，且L2又以3.5 m占主导地位，故取轴距L2为3.5 m。

2.4.2轴距L3的概率模型

轴距L3分布在4.47～21 m范围之间，采用Levenberg-Marquardt算法，对轴距L3的概率分布进行拟合，经K — S优度检验，轴距L3的概率分布不拒绝对数正态分布，且拟合的效果较好。拟合的分布参数见表6，拟合的概率分布曲线见图9。

表6 六轴超限车辆轴距L3的分布参数Table6 DistributionparametersforaxlebaseL3ofover-loadedvehiclewith6axles特征参数分布类型分布参数正规化常数k均值标准差轴距L3/m对数正态0.99792.3250.251

图9　概率分布曲线拟合图Figure 9　Fitting curve of probabilistic distribution

2.4.3轴距概率模型的建立

统计发现轴距L1Z与L1G之间有关联性，根据轴距L1Z和L1G的大小将图7所示的典型超限车类型细分成四小类(见图10)：

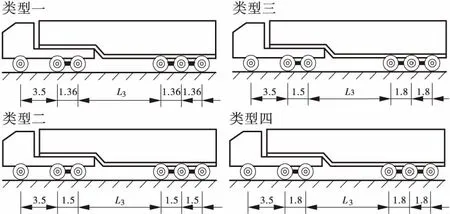
图10　六轴超限车按轴距大小分类图Figure 10　　　　Axle base-informed classification figure of the overloaded vehicle

轴距L3的数值在上述四类超限车辆中均随机分布在4.47～21 m范围之间，因此按上述4类超限车各自所占的比例和随机分配的轴距L3，即可建立六轴超限车辆轴距的概率模型，具体参数见表7。

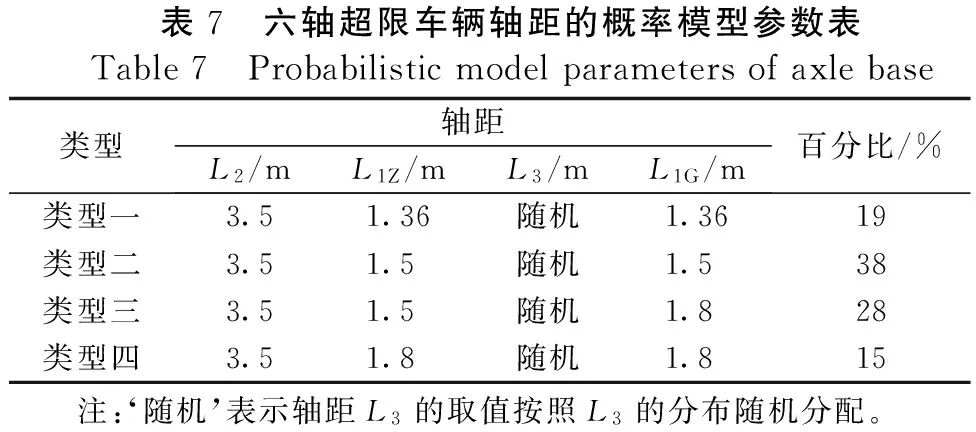
表7 六轴超限车辆轴距的概率模型参数表Table7 Probabilisticmodelparametersofaxlebase类型轴距L2/mL1Z/mL3/mL1G/m百分比/%类型一3.51.36随机1.3619类型二3.51.5随机1.538类型三3.51.5随机1.828类型四3.51.8随机1.815 注:‘随机’表示轴距L3的取值按照L3的分布随机分配。

3　随机生成超限车辆

根据建立的总重和轴距概率模型及总重和轴长(轴距之和)的关系，随机生成符合实际情况的超限车辆。对总重和轴长的数据进行统计，得到了五轴、六轴超限车辆的总重和轴长散点图(见图11)。可看出，不论是五轴超限车辆还是六轴超限辆，它们的总重和轴车之间没有明显关系，均是随机分布的。

图11　超限车辆总重—轴长散点图Figure 11　　　　Scatter diagram of complete weight with respect to axle length

3.1随机生成五轴超限车辆

3.1.1随机生成总重

五轴超限车辆包含图3所示的2种类型，其中类型一超限车辆的数量占总数的百分比为62%: 类型二超限车辆为38%。对两种类型的超限车辆总重进行统计分析发现，在总重小于550 kN的超限车辆数量中，类型一超限车辆所占的比例为86.5%，类型二超限车辆为13.5%。

根据拟合的五轴超限车辆总重的概率分布函数，采用蒙特卡洛(Monte Carlo)法[15]随机生成10000个五轴超限车辆总重。结合类型一和类型二超限车各自数量及总重的比例，进行随机分配，即可得到类型一和类型二超限车辆各自的随机总重。

加强水生态保护与修复 为全面开展水生态文明建设奠定基础…………………………………………………… 马 振(15.73)

3.1.2生成各轴轴重

除第一轴外，其余各轴的轴重按照五轴超限车辆总重与轴重的线性回归模型进行计算，而第一轴的轴重则按照总重减去其余各轴的轴重和得到。根据随机生成的类型一和类型二超限车辆的总重，按照上述原则即可得到各类型超限车辆各轴的轴重。

3.1.3随机生成轴距

基于拟合的五轴超限车辆轴距L3的概率分布函数，采用蒙特卡洛(Monte Carlo)法随机生成10000个五轴超限车辆轴距L3。根据表5中的相关参数，按照比例进行随机分配，即可得到类型一和类型二超限车辆的随机轴距。

3.1.4生成超限车辆

由于总重和轴长之间没有明显的相关关系，故按照总重和轴距随机配对的原则，即可随机生成10000辆五轴超限车辆。

3.2随机生成六轴超限车辆

由于六轴超限车辆只有一种类型，故根据拟合的六轴超限车辆总重概率分布函数，采用蒙特卡洛(Monte Carlo)法随机生成10000个超限车辆的总重，即可得到六轴超限车辆的随机总重。

3.2.2生成各轴轴重

与五轴超限车辆相同，除第一轴外，其余各轴的轴重按照六轴超限车辆的总重与轴重的线性回归模型进行计算，而第一轴的轴重则按照总重减去其余各轴的轴重和得到。根据随机生成超限车辆的总重，按照上述原则，即可得到六轴超限车辆各轴的轴重。

3.2.3随机生成轴距

基于拟合的六轴超限车辆轴距L3的概率分布函数，采用蒙特卡洛(Monte Carlo)法随机生成10000个六轴超限车辆轴距L3。根据表7中的相关参数，按照比例进行随机分配，即可得到六轴超限车辆的随机轴距。

3.2.4生成超限车辆

由于总重和轴长之间没有明显的相关关系，故按照总重和轴距随机配对的原则，即可随机生成10000辆六轴超限车辆。

4　荷载效应分析

根据五轴和六轴超限车辆的轮轴特征，按照前述生成超限车辆的方法，各随机生成10000辆超限车辆。选取跨径为8、10、13、16、20、25、30、40和50 m的简支梁桥，计算超限车辆的跨中最大弯矩效应。图12给出随机超限车辆和实际超限车辆的跨中最大弯矩效应的累计密度曲线。

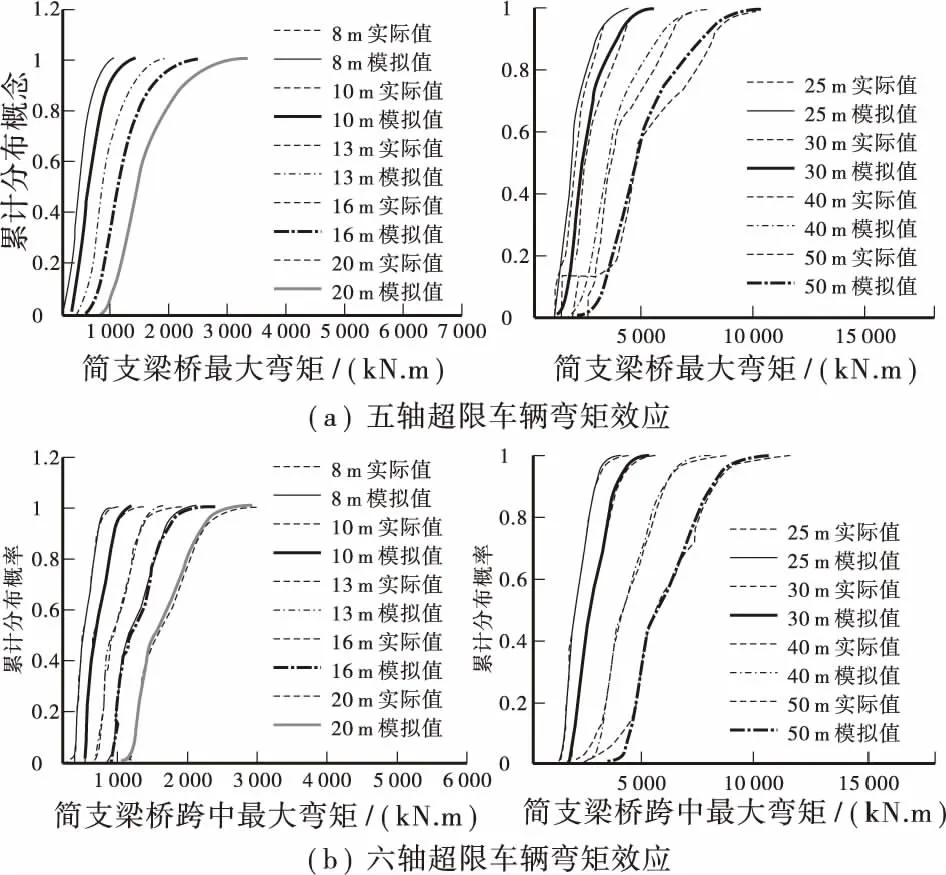
图12　弯矩效应的累计分布曲线Figure 12　Cumulative distribution curve of moment effect

对比二者的弯矩效应累计分布曲线可以看出：

① 随机生成的五轴超限车辆与实际五轴超限车辆的跨中最大弯矩效应累计分布曲线基本吻合；跨径大于40 m时，随机生成的五轴超限车辆弯矩效应累计概率在0.6～0.9区段的最大弯矩较实际超限车辆偏小；

② 随机生成的六轴超限车辆与实际六轴超限车的跨中最大弯矩效应累计分布曲线基本吻合；当跨径等于50 m时，随机生成的六轴超限车辆弯矩效应累计概率在0～0.1区段的最大弯矩较实际超限车辆偏大。

总体来说，随机生成的超限车辆与实际超限车辆的跨中最大弯矩效应基本上是一致的。也说明了前述随机生成超限车辆的方法是可行的。

5　结论

① 根据广西地区申请通行的五轴、六轴超限车辆的原始数据，基于概率统计分析理论，系统研究了超限车辆的总重、轴重和轴距等轮轴特征参数的概率分布，采用双峰正态分布和对数正态分布，建立了超限车辆的荷载模型；

② 采用蒙特卡洛(Monte Carlo)法各随机生成10000辆五轴、六轴超限车辆。对比了简支梁桥下，随机生成的超限车辆与实际超限车辆的跨中最大弯矩效应，验证了随机生成超限车辆方法的可行性；

③ 利用随机生成超限车辆的方法，可以为广西地区五轴、六轴超限车辆过桥时，桥梁的安全评估研究提供车辆荷载数据基础。

[1]熊慧中,李忠铭,王海涛,等.基于《公路桥梁技术状况评定标准》的桥梁评定管理系统开发[J].公路工程,2014,39(3):214-218.

[2]AASHTO, AASHTO LRFD bridge design specifications [S].Washington DC: America Association of State Highway and Transportation Officials, 2004.

[3]Jian Zhao, HabibTabatabai.Evaluation of a Permit Vehicle Model Using Weigh-in-Motion Truck Records [J].Journal of Bridge Engineering, 2012, 17(2): 389-392.

[4]Gongkang Fu, Osman Hag-Elsafi.Vehicular Overloads: Load Model, Bridge Safety, and Permit Cheching [J].Journal of Bridge Engineering,2000, 5(1): 49-57.

[5]César Crespo-Minguillbón, Juan R.Casas.A Comprehensi-ve Traffic Load Model for Bridge Safety Checking [J].Structural Safety,1997, 19(4): 339-359.

[6]刘青,张晓晖,陈建新,等.基于先验知识的高速公路逃费车辆跟踪算法研究[J].公路工程,2013,38(4):75-78.

[7]王强, 刘仰韶.公路桥梁汽车的轮轴特征[J].公路交通科技, 2013, 30(11): 41-52.

[8]党栋, 贺拴海,周勇军,等.基于车辆统计数据的汽车荷载标准取值与评估[J].长安大学学报:自然科学版, 2012, 32(6): 44-51.

[9]孙守旺, 孙利民.基于实测的公路桥梁车辆荷载统计模型[J].同济大学大学学报:自然科学版, 2012, 35(1): 198-204.

[10]郭彤, 李爱群,赵大亮.用于公路桥梁可靠性评估的车辆荷载多峰分布概率模型[J].东南大学学报:自然科学版,2008, 38(5): 763-766.

[11]梅刚, 秦权,林道锦.公路桥梁车辆荷载的双峰分布概率模型[J].清华大学学报, 2003, 43(10): 1394-1404.

[12]杨柳, 陈艳萍.求解非线性方程组的一种新的全局收敛的Levenberg-Marquardt算法[J].计算数学, 2008, 30(4): 388-396.

[13]林忠民.工程结构可靠性设计与估计[M].北京: 人民交通出版社, 1990, 244-252.

[14]何灿芝,罗汉.应用统计学[M].长沙: 湖南大学出版社, 2004, 98-109.

[15]贡金鑫, 魏巍巍.工程结构可靠性设计原理[M].北京: 人民交通出版社, 2007,103-110.

Statistical Load Model for Overloaded Vehicles Using Data Records

FU Xianming1, XIE Shangfei2, HE Huizhong1, YAN Banfu1

(1.Department of Civil Engineering, Hunan University, Changsha, Hunan 410082, China;2.Hunan Communications Research Institute, Changsha, Hunan 410015, China)

According to the data records of the overloaded vehicle from Guangxi Highway Administration, the bimodal Gaussian distribution and lognormal Gaussian distribution are employed to attain the probabilistic model for the axle load, axle base and complete weight of the overloaded vehicle with 5 or 6 axles in Guangxi region. The article presents the linear regression model for complete weight and axle weight and analyzes the relationship between complete weight and axle base of the overloaded vehicle. The Monte Carlo is used to randomly generate 10000 vehicles with 5 or 6 axles according to the statistical load models. The maximum bending moments of the simple-supported bridge with small and medium span under the action of the simulated overloaded vehicle models are compared to those under practical vehicles, which verified the effectiveness of the proposed overloaded vehicle model, and also supplies important data for vehicular permit checking and bridge safety assessment.

overloaded vehicle; load model; statistical model; linear regression; randomly generation

2015 — 03 — 12

符献民(1988 — )，男，湖南益阳人，硕士，主要从事公路桥梁的维护、管理和研究工作。

U 441+.2

A

1674 — 0610(2016)04 — 0212 — 06