动荷载作用下材料阻尼参数对Top-Down裂缝疲劳寿命的影响分析
杨一希, 陶国星, 郭 芳
(1.湖南交通职业技术学院, 湖南 长沙 410132; 2.长沙理工大学, 湖南 长沙 410014; 3.中交第二公路勘察设计研究院有限公司, 湖北 武汉 430000)
动荷载作用下材料阻尼参数对Top-Down裂缝疲劳寿命的影响分析
杨一希1,2, 陶国星3, 郭芳1
(1.湖南交通职业技术学院, 湖南 长沙410132;2.长沙理工大学, 湖南 长沙410014;3.中交第二公路勘察设计研究院有限公司, 湖北 武汉430000)
通过ABAQUS有限元软件建立带缝工作的二维路面模型,通过正弦波模拟车辆对路面的动荷载效应,通过虚拟闭合法,计算沥青路面Top-Down裂缝的应力强度因子K2,并探讨了考虑沥青混合料阻尼特征下,沥青路面的剪切型强度因子K2的变化规律,再进一步通过Paris模型,分析阻尼特征对Top-Down裂缝疲劳寿命的影响。以期为路面动态破坏研究提供一定的理论参考。
二维有限元; Top-Down裂缝; 应力强度因子; 阻尼比; 疲劳寿命
0 前言
在我国高等级沥青路面使用过程中,路面Top-Down裂缝属于较为典型且常见的路面病害之一,其特征表现为路面在车辆轮载剪应力的作用下,产生开裂,且裂缝沿着路表向下发展[1,2]。尽管Top-Down裂缝在发展初期对路面结构的完整性不构成威胁,但其影响也应得到足够的重视:一方面该类型裂缝发生在路表,雨水和其他杂质更容易侵入裂缝面,同时裂缝与车辆荷载直接接触,相对于路面结构性破坏,使得其更容易发展,并衍生出其他类型病害,如块裂,松散和坑槽等;另一方面,该类型病害往往出现在轮迹带附近,且沿路面纵向发展,且长度长,影响面积大,如任其发展,往往维修面积大,耗费较多的人力物力。
本文通过建立二维平面应变有限元模型,计算动荷载作用下含Top-Down裂缝沥青路面的应力强度因子K2在不同沥青混合料阻尼比情况下的变化规律,再通过Paris模型,分析材料阻尼特性对裂缝疲劳寿命的影响。以期能为路面设计和病害成因分析提供参考。
1 路面结构模型及数值计算
1.1带缝工作路面模型及动荷载模拟(见图1)
有限元分析取参照我国最为普遍的半刚性基层路面结构。力学模型为:假设一个带缝工作的半刚性路面结构,其开裂层位为沥青面层,同时当带缝路面结构受单轴双轮荷载时,裂缝位置于荷载作用面边缘[3],单轮作用力F=25 kN,荷载压强P=0.7 MPa,轮距和轮中心距δ均为0.186 m[4]。

图1 带Top-Down裂缝工作路面结构模型Figure 1 Pavement structure with Top-Down crack
为模拟标准车辆驾近和远离横断面的过程[5],采用正弦波模拟动荷载驶入驶出断面的过程:
(1)
式中:T为总作用时间,再根据公式:
(2)
式中:nw为荷载轴数,个;p为轮胎平均接地压力,MPa;B为轮胎接地宽度,186 cm;v为行车速度,km/h。
由上式可知:当T=0.007 5时,可反算出v=85 km/h。
1.2动力学理论及路面材料阻尼


(3)

在本次采用ABAQUS进行动荷载有限元分析时,物体的阻尼采用瑞利阻尼公式进行表达,即[C]=α[M]+β[K][5]。α为结构固有频率参数,β为阻尼参数,两参数与物体自振频率ω1和阻尼比λ1密切关联,且∂=λ1ω1,β=λ1/ω1。
1.3强度因子的计算方法(见图2)

(4)
在此基础上假设开裂前裂缝尖端位移同开裂后尖端位移相等。

(5)

(6)
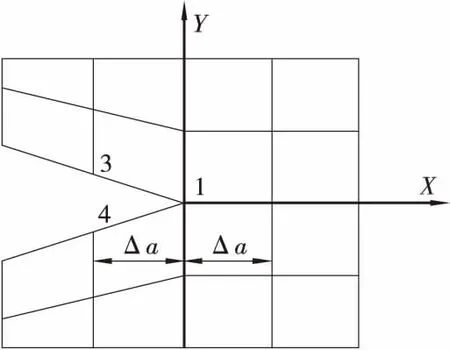
图2 虚拟闭合法网格划分及计算示意图Figure 2 Virtual closure mesh dividing and calculation schematic
该种计算裂缝强度因子的方法具有表达直接、计算简单等优点,裂缝尖端各参数都能通过ABAQUS有限元软件直接获取,同时该计算方法具有较高的精确性,将该方法计算的K1和K2值与解析解[6]作比较,相对误差仅为4%,表面了该方法的具有较好的可行行和精确性。
2 动荷载作用下应力强度因子变化规律
在进行路面结构动荷载计算时候,取沥青混合料自身振动频率ω1=12.5 Hz,沥青混合料阻尼参数β阻尼比分别为0.01,0.02,0.03和0(即不考虑材料本身阻尼特性)的情况下,同时忽略路面结构其他材料的阻尼特性,路面Top-Down裂缝长度为2 cm时,荷载作用力最大时刻,即t=0.003 75 s时,裂缝尖端的最大应力场,如图3所示。
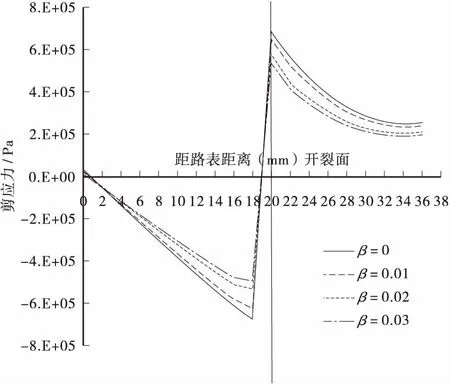
图3 不同阻尼参数情况下路面Top-Down裂缝尖端应力变化情况Figure 3 Crack-tip stress changes of pavement Top-Down crack in different damping parameter
由图3可以看出:沿裂缝面向下延伸,剪应力逐渐增大,在裂缝尖端位置产生奇异性,于裂缝处达到最大值,最终趋于平稳。同时由于沥青混合料阻尼特性的增强,对裂缝尖端剪应力有降低作用。
裂缝应力强度因子历时变化情况如图4所示。

图4 不同阻尼参数情况下路面Top-Down裂缝剪切型 应力强度因子K2历时变化Figure 4 Stress intensity factor changes over time of pavement Top-Down crack in different damping parameter
由上图可以看出,路面Top-Down裂缝的应力强度因子K2历时变化规律与荷载曲线有一定的相似性,有所不同的是,随着沥青混合料阻尼特性的增强,应力强度因子历时变化曲线出现了一定的后移,且波峰位置并非在荷载作用最大的时间点上,同时阻尼特性对降低应力强度因子具有一定的效果。
动荷载作用下,各长度裂缝所对应的应力强度因子的峰值,如表1所示。

表1 动荷载作用下各长度裂缝所对应的K2峰值(MPa·mm1/2)Table1 K2peakofdifferentlengthcrackunderdynamicloading裂缝长度/mmβ=0β=0.01β=0.02β=0.03202.742.62.31.9402.922.82.52.1603.233.12.72.3803.653.53.12.61004.204.03.53.01204.884.74.13.41405.675.44.84.01606.596.35.64.71807.637.36.45.4
3 动荷载作用下Top-Down裂缝的疲劳寿命
Paris认为,应力强度因子K既然是表征裂缝尖端应力场强弱的量,那么也是裂缝扩展速率的表达方式之一,则通过相关试验[7-9],建立积分关系,可以将裂缝长度和作用次数联系起来,具体表达式(7)如下:
(7)
式中:C和n分别为与沥青混合料弹性和蠕变特性相关的系数;强度因子增幅,在进行计算时,ΔK1为负数,即对裂缝扩展不起作用,即为0,ΔK2无论正负,对裂缝扩展均其作用;a1和aC为裂缝扩展前后的长度。
在对Top-Down裂缝进行疲劳寿命计算时候,遵循如下假设:
① 根据相关文献[1],在进行疲劳寿命计算时,C=2.38×10-6,n=1.38;
② 裂缝起裂长度[3]为20 mm,以裂缝最终穿透沥青面层为破坏标准;
③ 对于裂缝扩展速率,即应力强度因子随着裂缝长度的增幅,得到实际上并非为恒定值,进行疲劳寿命计算时,可以采用2种方法:第1种为采用拟合曲线得到拟合,一次性计算裂缝从起裂到破坏的疲劳寿命;第2种是假设裂缝在一定开裂长度内,应力强度因子增幅和裂缝长度的增加Δa呈线性关系,累加N值从而得到疲劳寿命,亦可观察裂缝在不同开裂阶段疲劳寿命情况,本文计算采用第2种方法,裂缝长度的增幅Δa为20 mm。
对于裂缝积分计算,采用matlab进行,以β=0时,裂缝从20 mm开裂至40 mm时为例。其线性关系为,Y=0.009 2X+2.553 6,则定积分计算公式为:
(8)
各开裂区间内疲劳寿命以及如图5所示。
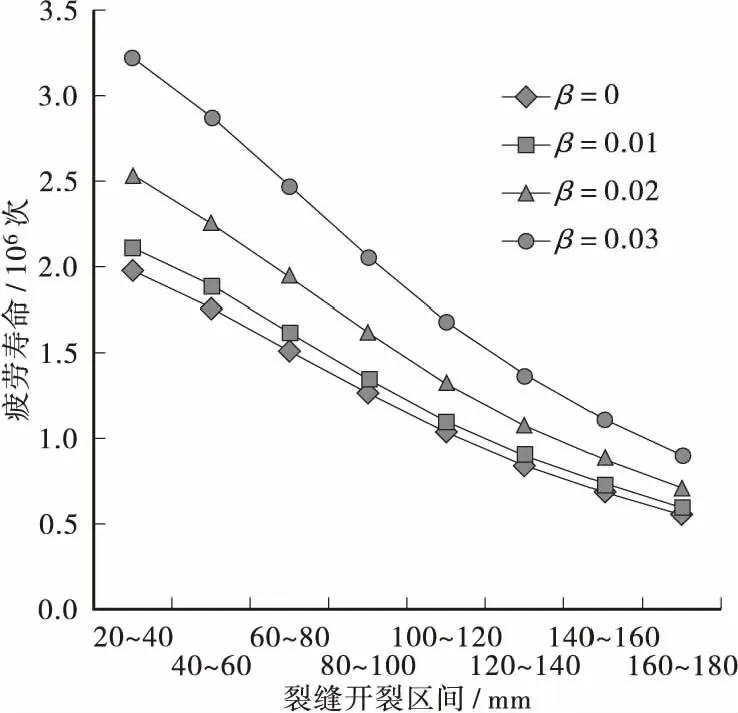
图5 各开裂区间内疲劳寿命Figure 5 Fatigue life of each cracking section
由上图可以看出:得益于沥青混合料的阻尼特性,于各个开裂区间内疲劳寿命均有所提高,其中以20~40 mm范围内疲劳寿命最长,随着开裂进程的增加,其疲劳寿命逐渐减小,并在各阻尼情况下,疲劳寿命趋于一致。
对各区段的疲劳寿命进行累加,以Top-Down裂缝贯穿面层为破坏标准,则在β=0,0.01,0.02,0.03时,裂缝疲劳寿命依次为9.6,10.3,12.3,15.7(106次),增幅分别为7.3%,28%和63.5%。
4 结语
本文通过ABAQUS建立二维有限元模型对带Top-Down裂缝工作的路面结构模型进行动态加载,分析裂缝的力学响应以及疲劳寿命,有以下结论:
① 于不同阻尼特性情况下,阻尼高的沥青混合料能有效降低裂缝尖端的剪应力。
② 在动荷载作用下,应力强度因子K2K2历时变化规律与荷载曲线基本类似,但随着沥青混合料阻尼特性的增加,使得应力强度因子历时变化曲线出现了后移,同时阻尼特性对降低裂缝尖端应力场强度具有一定的效果。
③ 增强沥青混合料的阻尼特性的增强有助于沥青路面Top-Down裂缝的疲劳寿命的增加,且在开裂初期表现的尤为明显,但随着裂缝的扩展,其抗裂效果逐渐降低,表现为各阻尼特性下,其疲劳寿命趋于一致。
④ 国内现在对沥青混合料阻尼特性研究较少,如何从沥青混合料级配、材质等方面入手,尚处于空白阶段,根据有关类似的研究[10-11],在混凝土中掺入适量的外加成分,如硬质纤维和橡胶颗粒等,可以提高其阻尼特性,且对强度影响甚小,在沥青路面抗裂设计中该方法值得借鉴。
[1]李峰,孙立军.沥青路面Top-Down开裂成因的有限元分析[J].公路交通科技,2006,23(6):1-4.
[2]Roque R,Birgisson B,Drakos C,et a1.Development and field evaluation of energy-hased criteria for Top-Down cracking performance of hot mix asphalt[J].Journal of the Association of Asphalt Paving Technologists,2004,73:229.
[3]易昕.三维有限元方法分析沥青路面自上而下裂缝的扩展[D].长沙:湖南大学,2006.
[4]毛成.沥青路面裂纹形成机理及扩展行为研究[D].成都:西南交通大学,2006.
[5]廖公云,黄晓明.ABAQUS有限元软件在道路工程中的应用[M].南京:东南大学出版社,2008,153-199.
[6]解德,钱勤,李长安.断裂力学中的数值计算方法及工程运用[M].北京:科学出版社,2009.
[7]Li Y Q,Metcalf John B.Fatigue Characteristics of Asphalt Concrete from Asphalt Slab Tests.Journal of Materials in Civil Engineering,2004,1 6(4):306.314.
[8]Mahboud KC,Liu Yinhui,Allen DL.Asphalt overlay and subsur-face drainage of broken and seated concrete pavement [J].Journal of Transportation Engineering,2005,131(8):617-622.
[9]Diyar Bozkurt.Three Dimensional Finite Element Analysis to Evaluate Reflective Cracking Potential in Asphalt Concrete Overlays[D].University of Illinois,PHd,2002.
[10]万泽青,刘平,施伟.高阻尼混凝土的试验研究及阻尼机理探讨[J].混凝土,2007(7):37-40.
[11]汪梦甫,宋兴禹.高阻尼混凝土构件阻尼性能研究[J],振动与冲击,2011(11):173-179.
Material Damping Parameters Under Dynamic Loading on Top-Down Crack Fatigue Life Analysis
YANG Yixi1,2, TAO Guoxing3, GUO Fang1
(1.Hunan Communication Polytechnic,Changsha, Hunan 410132, China;2.Changsha University of Science & Technology,Changsha, Hunan 410014, China;3.CCCC Second Highway Consultant Co.Ltd ,Wuhan, Hubei 430000, China)
This paper via ABAQUS finite element software,established 2D pavement model working with crack.simulating dynamic load effects on the road by sine wave,using Virtual closing legal,asphalt pavement crack stress intensity factor K2are calculated,and the sametime,Material damping parameters are considered,to discover the variation of K2,then using Paris formula,analysis the fatigue life effected by material damping parameters.In order to provide a theoretical reference of pavement dynamic damage study.
2D-finite element model; Top-Down crack; stress intensity factor; damping parameter; fatigue life
2016 — 04 — 14
湖南省教育厅科学研究项目(14C0409);湖南省交通运输厅科技进步与创新项目(201414)
杨一希(1982 — ),男,湖南冷水江人,硕士,讲师、工程师,主要从事高职路桥专业教学和研究。
U 418.6
A
1674 — 0610(2016)04 — 0108 — 04

