矩匹配和变分方法相结合的M O DIS条带去除模型

胡宝鹏，周则明，孟 勇，张水平（解放军理工大学气象海洋学院，江苏　南京211101）

矩匹配和变分方法相结合的M O DIS条带去除模型

胡宝鹏，周则明，孟 勇，张水平
（解放军理工大学气象海洋学院，江苏南京211101）

针对中分辨率成像光谱仪（m oderate resolution imaging spectroradio meter，M O DIS）影像常见的3种条带噪声，提出了一种矩匹配和变分相结合的多类条带噪声去除模型。首先采用矩匹配方法对M O DIS影像做预处理，然后基于变分方法去除条带噪声。能量泛函由L1正则化项、数据保真项和梯度保真项组成，基于Split Breg man迭代计算能量泛函的最优解。实验结果表明，此算法能够有效地去除M O DIS影像中常见的条带噪声。与矩匹配、低通滤波及单向全变分方法相比，此模型更好地保留了图像的细节信息，有效抑制了正则化方法在条带去除过程中出现的分块现象。

中分辨率成像光谱仪影像；条带噪声；变分条带去除；Split Breg man迭代

网址：w w w.sys-ele.co m

0 引 言

条带噪声是一种存在于遥感影像中的具有周期性、方向性且呈带状分布的特殊噪声，其原因在于遥感器各探测单元的物理响应存在着一定的差异，沿探测器阵列方向产生了起伏。图1所示为中分辨率成像光谱仪（m oderate resolution imaging spectroradio meter，M O DIS）影像中常见的单行、多行及宽行等3种类型的条带噪声。

遥感影像条带噪声的去除主要有两类方法：一类是以直_方_图_匹_配、矩匹配［1 4］为代表的、对图像灰度值进行归一化和匹配的方法；另一类是空间-频率域滤波法［5 7］。第一类方法容易实现，但要求噪声图像中地物分布均一；第二类方法计算复杂，且对于地物分布复杂的遥感影像，常常在条带去除过程中丢失图像中的某些细节。近年来在条带噪声去除方面的工作包括：文献［8］基于二维方向滤波器结合均值补偿技术去除遥感影像中的非周期性条带；文献［9］利用扫描角度高于探测器瞬时视场重叠部分的冗余信息建立均衡化曲线以去除条带；文献［10］提出了一种直方图匹配与迭代最小二乘面滤波相结合的分步条带去除算法；文献［11］对图像进行形态学处理，从而获取各像元的校正参数来去除条带。目前，基于变分的图像处理技术已经成为研究的热点，R O F［12］模型能够在去除噪声的同时有效地保持图像的边缘信息［12］。文献［13］研究了条带噪声的特性，在R O F模型的基础上提出了单向全变分条带去除模型。文献［14］在H uber-M arkov正则化模型的基础上，利用最大后验概率方法进行条带去除。文献［15］利用压缩感知和单向全变分相结合的方法同时去除图像中的随机噪声和条带噪声。

图1 M O DIS条带噪声类型

本文提出了一种矩匹配和变分方法相结合的分步条带去除算法，其能量泛函由L1正则化项、数据保真项、梯度保真项组成，模型在去除条带噪声的同时能够有效地保持图像中的细节信息，抑制正则化方法在图像处理过程中出现的分块现象。

1 条带去除模型与数值计算方法

根据中分辨率成像光谱仪的成像原理［16］，可将M O DIS数据中的条带噪声视为加性噪声，假设观测图像为f（x，y），条带去除后的图像为u（x，y），加性噪声为n（x，y），则条带噪声模型可表示为

对于M O DIS数据中的多行和宽行条带噪声，由于M O DIS影像行数据与遥感器各探测单元位置严格对应，因此可将其拆分为相应子图，选择某一无条带子图作为参考，将其余子图与其做矩匹配处理，然后再基于变分模型去除剩余的条带；对于单行条带噪声，则可以直接使用变分条带去除模型求解。图2为变分条带去除模型的流程图。

图2 变分条带去除模型流程图

矩匹配法将不同探测单元对应的图像行数据的标准差和均值做归一化处理。在地物分布均一的理想情况下，对于一幅大幅面M O DIS影像，各C C D按行扫描所获取的数据，其入射辐射强度的均值和方差近似相等［16］。因此，选取某一理想的、具有标准响应函数C C D行数据作为无条带子图，将该子图的均值和方差作为参考，通过线性变换，将其他探测单元的均值和方差调整到该探测单元，能够较有效地达到条带去除的目的，其变换公式为

式中，X，Y分别为第i行图像像素校正前后的灰度值；σr，μr为参考探测单元行数据的标准方差、均值；σi，μi为第i个探测单元行数矩的标准方差、均值。

矩匹配方法现已广泛应用于遥感图像的去噪，但矩匹配后的M O DIS图像仍然存在条带噪声。因此，针对条带噪声的特点，定义如下能量泛函：

式中，Ω1=｛（x，y）∶|xf（x，y）|＜|f（x，y）|∩|f（x，y）|＜η｝，η为一小的正常数。对于条带区域，一般有|xf（x，y）||yf（x，y）|，因此当η较小时，Ω1近似于条带区域。能量泛函式（3）中，第一项为L1范式，确保去条带过程中的各向异性扩散，以有效地保持图像中目标的边缘；第二项为数据保真项，用于保持非条带区域中去条带前后图像数据的一致性；第三项为梯度保真项，用于保持非条带区域中图像的梯度场信息，避免由于L1正则化而出现的图像分块现象。λ1，λ2为非负的权重系数，用来调节各能量项对条带去除结果的影响。

由于泛函模型（3）含有非光滑的L1范数，本文采用Split Breg man迭代算法求解。对于泛函模型（3），引入辅助变量dx=Δxu，dy=Δyu，其中Δu=（Δxu，Δyu），d=（dx，dy），将含有L1正则化项的无约束优化问题转换为带约束的优化问题，即

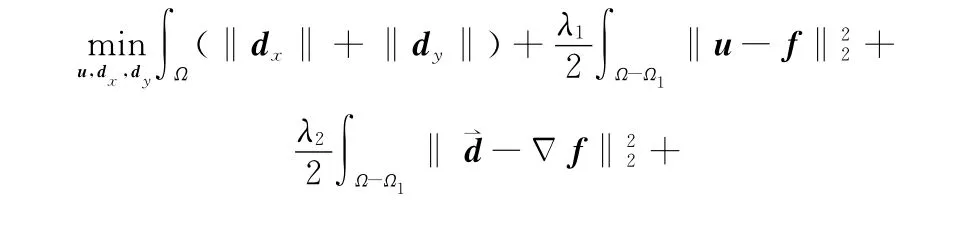
采用增广拉格朗日乘子法可将式（5）转换为

使用Breg man迭代求解问题（6）（为书写方便，省略积分号），得：

式（7）中的u，dx，dy之间互不耦合，因此可转化为以下三个子问题的求解：

式中，u的求解是一个可微分最优化问题，对应的Euler—Lagrange方程为

令

则式（11）等价于

F为快速傅里叶变换（fast Fourier transform，FF T），F-1为逆FF T，Δ为Laplacian算子。uk+1的显式表达式为

迭代计算式（8）、式（9）、式（13）、式（14）和式（15），当残差‖u-f‖2/‖f‖2＜ε或者迭代达到一定的次数后，计算终止，得到条带去除后的图像u。FF T的时间复杂度为O（NlogN），N为图像的大小，因此算法总的时间复杂度为O（tNlogN），其中t为迭代的次数。

综上所述，能量泛函（3）最优解的Split Breg man迭代过程如算法1所示。

2 实验与分析

为了验证本文算法的有效性，根据http：∥ladsweb.nasco m.nasa.gov网站提供的2002年3月15日的Terra M O DIS数据，分别选取含有单行、多行和宽行条带的第33、30和27波段图像进行条带去除实验。由于原图较大，本文只给出实验结果的子图，其大小为512×512。

本文根据实验和启发式规则设置模型中的参数：L1正则化项用于去除条带，数据保真项用于保持去除条带前后非条带区域数据的一致性，梯度保真项则用于保持图像中目标的细节，因此可根据应用需求适当调整各个能量项的权重系数。实验表明，本文模型中的参数设置为λ1=100，λ2=5，γ= 103，η=0.1，最大迭代次数为100，迭代终止的条件为：‖uk+1-uk‖2/‖f‖2＜10-3能够取得较理想的条带去除效果。单向全变分模型［13］的参数设置为：△t=0.01，λ=0.5，迭代终止的条件为：‖uk+1-uk‖2/N＜10-4，其中N为图像的大小。

为了客观评价条带噪声去除的效果，使用变化逆系数（inverse coefficients of variation，IC V）［17］和辐射质量提升因子（im provement factors of radio metric quality，IF）［18］作为评价指标。设Ra为条带去除后图像中指定窗口大小内灰度的均值，Rsd为标准差，则IC V定义为

IC V值越大，条带去除效果越好。指定的窗口一般为10× 10像素大小的均匀区域。

IF定义为条带去除前后两幅图像在条带分布方向上灰度的变化，计算公式为

式中，mIR（i），mIE（i）分别代表两幅图像条带去除前后第i行均值。IF取值越大，表明算法的条带去除能力越强。

2.1 单行条带去除

对于第33波段带有单行条带噪声的图像，直接采用变分条带去除模型进行处理，并与矩匹配［1］，低通滤波（5× 5），单向全变分［13］算法的条带去除效果进行比较，图3所示为各方法的条带去除结果。

图3 Terra-M O DIS 33波段条带去除结果

从图3可以看出，低通滤波和矩匹配方法能够在一定程度上去除条带噪声，但上述两种方法的去除效果一般，图像中依旧残留少量的条带。本文模型和单向全变分方法去条带效果较好，能最大程度地抑制条带噪声、保持图像的细节信息。从局部放大图来看，本文模型得到的去噪图像更加光滑，视觉效果更加自然，较好地消除了单向全变分方法中出现的分块现象。图4所示为各算法条带去除前后图像行均值的变化曲线。

图4 Terra-M O DIS 33波段各行均值

从图4可以看出，相比原图像的行均值曲线呈现出的上下剧烈波动和随机起伏，常规矩匹配方法的行均值曲线与原图相比几乎没有太大的变化。低通滤波方法的均值曲线中依然有轻微的毛刺现象，而单向全变分和本文算法的行均值曲线更为平滑，说明这两种方法的条带噪声去除能力更强。

图5为单向全变分算法和本文算法的去条带图像傅里叶变换频谱图，图5（b）、图5（c）与图5（a）的频谱结构相似，表明本文算法与单向全变分算法均能有效去除条带噪声并保持原图像的细节信息，本文算法的单行条带去除性能近似于单向全变分算法。

图5 Terra-M O DIS 33波段频谱图像

2.2 多行、宽行条带去除

针对图像中的多行和宽行条带噪声，为了获得优良的去噪效果，首先采用矩匹配方法进行预处理，然后再使用变分模型去除剩余的条带。

M O DIS采用多元并扫方式成像，实验采用的Terra M O DIS 1k m分辨率图像是10元并扫。在矩匹配处理前需要对M O DIS数据重组以将各探测单元与图像区域相对应。以第27波段图像为例，假设其第一行数据由M O DIS传感器的第一个探测器扫描构成，第二行数据由第二个探测器扫描构成，以此类推，可将原始影像划分为10幅子图，图6给出了M O DIS影像的1～10号探测器子图像。

如图6所示，第27波段的1～10号探测器中，第7、9号子图存在较为明显的条带，第8、10号子图含有轻微的条带噪声。本文采用不含条带噪声的1号子图作为参考，其余子图与1号子图做矩匹配处理。

图6 Terra-M O DIS 27波段的110号探测器子图像

将矩匹配后的子图重新组合为整幅图像，使用本文提出的变分模型进行条带去除处理。图7所示为第30、27波段图像分别使用矩匹配［1］、低通滤波（5×5）、单向全变分［13］和本文算法的条带去除结果。

从图7、图8可以看出，与原图相比，低通滤波和矩匹配方法均能够部分地消除条带噪声，但仍含有较多的条带残留。单向全变分方法对弱条带噪声去噪效果较好，而对强条带噪声其去噪后的图像有着明显的分块现象，如图7（d）、图7（e）和图8（d）、图8（e）中红框部分对应的局部放大图所示。从目视效果上来看，本文方法去除条带较为彻底，图像的边缘等细节信息保留较好。

图7 Terra-M O DIS 30波段条带去除结果

图8 Terra-M O DIS 27波段条带去除结果

图9和图10分别给出了第30、27波段图像各方法条带去除前后行均值的变化情况。由于条带噪声的干扰，原图像行均值分布呈现剧烈的波动，矩匹配方法能够部分抑制条带噪声，行均值曲线较为平缓。低通滤波的平滑效果比较明显，但同时也损失了图像中的细节信息。单向全变分及本文算法的平滑效果和细节保持能力均较强，但对于强条带和宽行条带噪声，本文算法的行均值曲线更加平滑、条带去除性能相对更优。

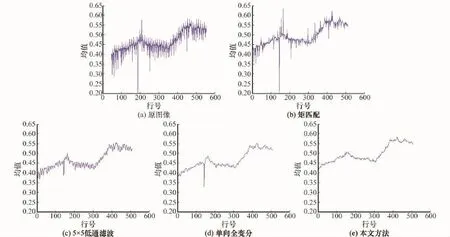
图9 Terra-M O DIS 30波段各行均值图

图11、图12为单向全变分方法和本文算法的去条带图像傅里叶变换频谱图。原图像在Y轴上有均匀分布的亮斑，表明图像中含有周期性的条带噪声。图11（b）、图12（b）在Y轴上的亮斑消失，但在其左右两侧出现了对称的细微条纹，如图中放大区域所示，说明单向全变分方法在条带去除过程中引入了其他噪声。图11（c）、图12（c）均消除了周期性分布的亮斑，同时保持了原图像的其他频谱信息。

图10 Terra-M O DIS 27波段各行均值图

图11 Terra-M O DIS 30波段频谱图像

图12 Terra-M O DIS 27波段频谱图像

为定量地比较各条带去除算法的效果，表1给出了第33波段、第30波段、第27波段的IC V和IF值。

表1 Terra-M O DIS 33、30、27波段条带去除结果客观评价指标

从表1可知，与矩匹配、低通滤波、单向全变分方法相比，本文提出的条带去除模型的IC V和IF指标值整体较高。表中低通滤波算法第33波段的IC V值最高，说明该算法出现了过平滑现象。综合主观评价和客观定量指标，本文算法取得了更优的条带去除结果。

3 结 论

本文提出了一种矩匹配和变分方法相结合的M O DIS影像条带噪声去除模型，以有效地去除多种类型的条带噪声。从实验结果来看，与其他方法相比，本文算法在去除条带噪声的同时，较好地保持了图像的细节并有效地抑制了L1正则化带来的分块效应，条带去除后的图像具有更好的视觉效果。本文模型中的参数需要通过实验设置，如何根据图像特性自适应地选择各能量项的权重系数还需要进一步的研究。

［1］Gadallah F L，Csillag F，S mith E J M.Destriping m ultisensor imagery with m o ment matching［J］.International Journal ofRemote Sensing，2000，21（12）：2505-2511.

［2］Chen J S，Shao Y，Zhu B Q.Destriping in C M O DIS data by a im proved m o ment matching［J］.Remote Sensing Technology and A pplication，2003，18（5）：313-316.（陈劲松，邵芸，朱博勤.一种改进的矩匹配方法在C M O DIS数据条带去除中的应用［J］.遥感技术与应用，2003，18（5）：313-316.）

［3］H orn B K P，W oodha m R J.Destriping landsat M SS imagery by histogram m odification［J］.Com put Graph&Im age Process，1979，10：69-83.

［4］W egener M.Destriping multiple sensor imagery by improved histogrammatching［J］.International Journal ofRemote Sensing，1990，11（5）：859-875.

［5］Chen J S，Shao Y，Zhu B Q.Destriping C M O DIS based on FIR method［J］.Journal of Remote Sensing，2004，8（3）：227-233.（陈劲松，邵芸，朱博勤.中分辨率遥感图像条带噪声的去除［J］.遥感学报，2004，8（3）：227-233.）

［6］Chen J S，Shao Y，G uo H D，et al.Destriping C M O DIS data by power filtering［J］.IE E ETrans.on Geoscience andRemote Sensing，2003，41（9）：2119-2124.

［7］Chen J S，Lin H，Shao Y，et al.O blique striping rem ovalin rem ote sensing imagery based on wavelet transform［J］.International Journal of Remote Sensing，2006，27（8）：1717-1723.

［8］Shi G M，W ang X T，Zhang L，et al.Rem oval of rando m stripe noises in rem ote sensing image by directionalfilter［J］.J.Infrared Millim.W aves，2008，27（3）：214-218.（石光明，王晓甜，张犁，等.基于方向滤波器消除遥感图像孤立条带嘈声的方法［J］.红外与毫米波学报，2008，27（3）：214-218.）

［9］Bisceglie MD，Episcopo R，Galdi C，et al.Destriping M O DIS data using overlapping field-of-view method［J］.IE E E Trans.on Geoscience and Remote Sensing，2009，47（2）：637-651.

［10］Rak watin P，Takeuchi W，Yasuoka Y.Stripe noise reduction in M O DIS data by combining histogram matching with fi lter［J］. IE E E Trans.on Geoscience and Remote Sensing，2007，45（6）：1844-1856.

［11］G uo L L，W u Z P，Zhang L G，et al.Destriping ofremote sensing images with applications to push-broom-type cameras［J］.Acta Optica Sinica，2013，33（8）：0828001.（郭玲玲，吴泽鹏，张立国，等.推扫式遥感相机图像条带噪声去除方法［J］.光学学报，2013，33（8）：0828001.）

［12］Rudin L，Osher S，Fatemi E.Nonl inear total variation based noise removal algorithms［J］.Physical D，1992，60（2）：259-268.

［13］Bouali M，Ladjal S.Toward optimal destriping of M O DIS data using a unidirectional variational m odel［J］.IE E E Trans.on Geoscience and Remote Sensing，2011，49（8）：2924-2934.

［14］Shen H F，Zhang L P.AM A P-based algorith m for destriping and inpainting of rem otely sensed images［J］.IE E E Trans.on Geoscience and Remote Sensing，2009，47（5）：1492-1502.

［15］Chang Y，Yan L X，Fang H Z，et al.Sim ultaneous destriping and denoising for rem ote sensing images with unidirectional total variation and sparse representation［J］.IE E E Geoscience and Remote Sensing Letters，2014，11（6）：1051-1055.

［16］Liu Z J，W ang C Y，W ang C.Destriping imaging spectro meter data by im proved m o ment matching method［J］.Journal of Remote Sensing，2002，6（4）：279-284.（刘正军，王长耀，王成.成像光谱仪图像条带去除的改进矩匹配方法［J］.遥感学报，2002，6（4）：279-284.

［17］Corsini G，Diani M，Walzel T.Striping removalin M OS-B data［J］. IE E E Trans.on Geoscience and Remote Sensing，2000，38（3）：1439-1446.

［18］Nichol J E，Vohora V.Noise over water surfaces in landsat T M images［J］.International Journal ofRemote Sensing，2004，25（11）：2087-2093.

周则明（1966-），通讯作者，男，副教授，硕士研究生导师，博士，主要研究方向为计算机视觉、模式识别与图像处理。

E-mail：zhou_zeming@yahoo.com

孟 勇（1990-），男，硕士研究生，主要研究方向为模式识别、图像处理。

E-mail：lgdam y@163.com

张水平（1975-），男，副教授，博士，主要研究方向为遥感图像处理、模式识别。

E-mail：shuiping mail@163.com

Destriping model of M O DIS images by com bining moment matching with variational approach

H U Bao-peng，Z H O U Ze-ming，M E N G Yong，Z H A N G Shui-ping
（Institute of Meteorology and Oceanography，P L A University of Science and Technology，Nanjing 211101，China）

A novel noise-reduction model is proposed to remove the multi-type stripe noises by combining moment matching with variational-based method，based on analyzing the characteristics of three types of stripe noises in moderate resolution imaging spectroradio meter（M O DIS）data.Firstly，moment matching method is em ployed for preprocessing the M O DIS imagery.Secondly，the variational method is performed to remove the stripe noises leftin the image.The energy functional consists of L1regularization term，image data fidelity term and image gradient fidelity term.Split Brg man iteration is adopted to achieve the optimization solution of the proposed energy functional.Experimental results indicate that the proposed model can reduce stripes in M O DIS data effectively.Co m pared with destriping approachesincluding moment matching，low-pass filter and unidirectional variational destriping，the proposed model can preserve the details of the M O DIS image and alleviate the block effects caused by regularization-based methods better.

moderate resolution imaging spectroradio meter（M O DIS）images；stripe noise；variational stripe rem oval；Split Breg man iteration

T P 391.4

A

10.3969/j.issn.1001-506 X.2016.03.35

1001-506 X（2016）03-0706-08

2014-10-22；

2015-07-07；网络优先出版日期：2015-11-12。

网络优先出版地址：http：//w w w.cnki.net/kcms/detail/11.2422.T N.20151112.1436.004.html

国家自然科学基金（41174164，41275029，41305138，61473310）；公益性行业（气象）专项（G Y H Y201306068）资助课题

胡宝鹏（1984-），男，硕士，主要研究方向为模式识别、图像处理。

E-mail：baopeng_hu@163.com